工程制圖中兩正交圓柱體相貫線的教學探討
程剛 盧淑群

摘 要 針對兩正交圓柱體相貫線的形狀特征和投影規律,通過空間曲線方程推導了兩正交圓柱體相貫線在非積聚性投影面投影為雙曲線或直線,對于空間曲線的投影直觀性較差的問題,通過三維建模軟件表達了直徑變化時兩正交圓柱體相貫線演變趨勢,結合實際操作并給出了兩圓柱體相貫線的求解流程圖。
關鍵詞 工程制圖 正交圓柱體 相貫線 投影
中圖分類號:G424 文獻標識碼:A ? DOI:10.16400/j.cnki.kjdkx.2015.09.038
Two Orthogonal Cylinders Intersecting Lines
Teaching in Engineering Drawing
CHENG Gang[1][2], LU Shuqun[3]
([1] Anhui University of Science & Technology, Huainan, Anhui 232001;
[2] Anhui Mine Mechanical and Electrical Equipment Collaborative Innovation Center, Huainan, Anhui 232001;
[3] School of Mechanical and Automotive Engineering, Chuzhou University, Chuzhou, Anhui 239000)
Abstract For shape characteristics and laws of the two orthogonal projection cylinders intersecting line space curve equation was derived by two orthogonal lines intersecting cylinders in the accumulation of non-hyperbolic or linear projection surface projection, the projection of the space curve intuitive when the problem of the poor, expressed by three-dimensional modeling software change in diameter of two orthogonal lines intersecting cylinders evolution trend, combined with the actual operation and gives a flowchart for solving the two cylinders intersecting lines.
Key words engineering drawing; orthogonal cylinder; intersecting Line; projection
0 前言
相貫線是工程制圖中重、難點教學內容。教材中關于相貫線的定義是:“兩立體表面的交線稱為相貫線。”兩曲面立體表面的相貫性一般是封閉的空間曲線,其形狀取決于曲面立體的形狀、大小和它們軸線的相對位置。求作時,首先是判定相貫線的形狀特點,再根據相貫線各投影特點,作出投影圖。在教學實踐中,由于相貫性的相對抽象性,學生很難理解并正確作圖,究其原因是在于:一是沒有深度地理解相貫線的形狀特征;二是沒有通過三維模擬技術生動表達出相貫性的形成原理。文章以兩正交圓柱體相貫線為例,針對上述問題做一些教學上的探討研究。
1 數學分析
教材中針對兩正交圓柱體相貫線的作圖方法和步驟敘述較多,而對于其相貫線的由來或形狀的準確描述很少。準確描述曲線在于利用數學語言來求解相貫線上點的運動軌跡,求出其對應方程。方程在邏輯上的優勢對于工科學生來說更具備深刻記憶的特征,一旦相貫線方程和投影方程被確定,對應的曲線形狀通過前期數學知識的積累,學生將會很容易地搜索到曲線的特征,這對后面找點近似描出相貫線投影具有很強的提示作用,從而強化了形狀預判的理論根據。
1.1基本理論
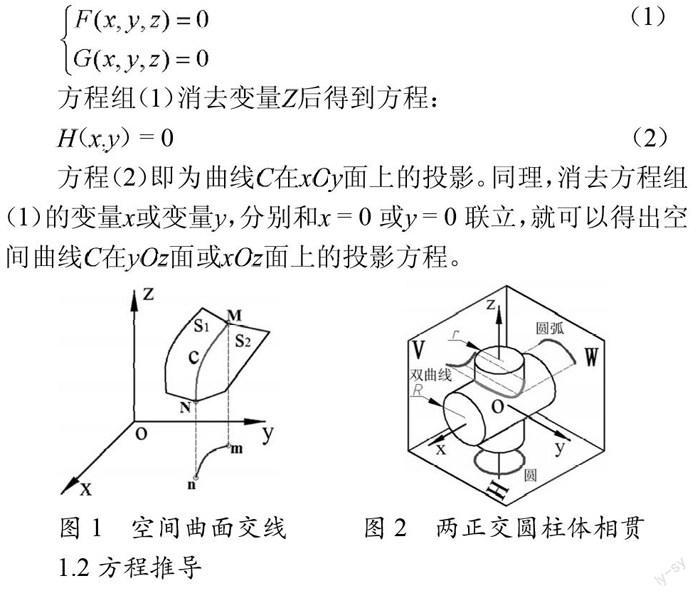
從高等數學上可以獲知,空間曲線可以看作兩個曲面的交線,如圖1所示。假設兩曲面的方程分別為:(,,)=0,(,,)=0,它們所產生的空間交線為,的任意點坐標均滿足兩曲面的方程,因此交線的一般方程為:
(1)
方程組(1)消去變量后得到方程:
()=0(2)
方程(2)即為曲線在面上的投影。同理,消去方程組(1)的變量或變量,分別和=0或=0聯立,就可以得出空間曲線在面或面上的投影方程。
圖1空間曲面交線圖2兩正交圓柱體相貫
1.2方程推導
根據上述空間曲線方程和空間曲線在坐標面上的投影理論,對于兩正交圓柱體,如圖2所示。其相貫線(圓柱面交線)方程為:(3)
消去變量,可得出兩正交圓柱體的相貫線在面上的投影方程組為:=(4)
從圖2中可以看出:相貫線在面和面上的因投影具有積聚性特點,判斷較易,為圓弧或整圓。兩圓柱體是正交,前后對稱,因而相貫線在面上的投影即可以看作在面上的投影,方程組(4)便可描述。通過對方程組(4)的分析可以得出,其表達式為雙曲線形式(=情況除外)。
當=時,方程組(4)簡化為:
(5)
此時為兩個相等直徑的正交圓柱體相貫,其面投影從雙曲線轉變為直線相交形式,類似于“住焙擰?
2三維輔助模型
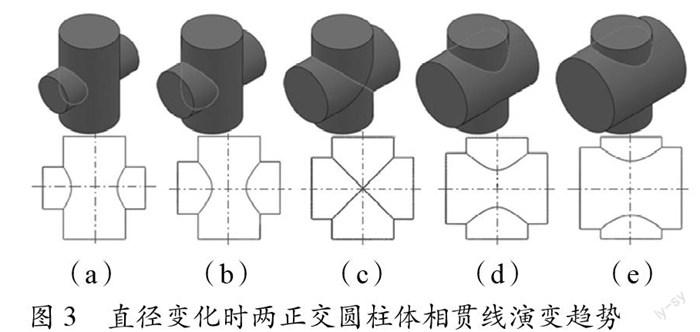
實踐教學中,學生對相貫線的形成過程和相關規律并不能理解透徹、融會貫通,原因在于學生對于三維轉換成二維的思維過程沒有徹底解放,而且相貫線相對其它形體投影又比較抽象,空間曲線的投影往往給學生造成巨大的困惑。直觀度較差是學生無法充分領會相貫線特性的重要障礙。因而,在實踐教學中,為了讓學生能從充分認知相貫性的形成過程和投影規律,利用現階段成熟的三維建模軟件,配合相關的動畫技術,建立三維模型的動態效果來幫助學生建立起空間概念是非常有必要的。常用的三維建模軟件有AutoCAD、Solidworks、Pro/E、Catia、3dmax等等,實際上在當前的機械設計過程中,三維模型造型已經滲透到設計諸多環節中,亦成為工程師繪制工程圖重要的輔助參考,可以說三維造型技術與二維繪圖已融為一體。對兩正交圓柱體相貫線投影特性,借以三維建模軟件,繪制出兩正交圓柱體相貫時,豎直圓柱直徑不變而水平圓柱直徑改變時,相貫線的變化趨勢與規律。如圖3所示。
(a)(b)(c)(d)(e)
圖3直徑變化時兩正交圓柱體相貫線演變趨勢
結合前文對兩正交圓柱體相貫線的數學方程的推導結論,通過建模軟件的三維造型功能,從圖3可以看出直徑變化時兩正交圓柱體相貫線演變趨勢為:豎直圓柱直徑不變而水平圓柱直徑改變時,當豎直圓柱直徑大于水平圓柱直徑時,相貫線在非積聚性投影面上投影為左右對稱的兩條雙曲線;當豎直圓柱直徑等于水平圓柱直徑時,相貫線在非積聚性投影面上投影為兩條直線,類似于“住焙牛壞筆痹倉本緞∮謁皆倉本妒保喙嵯咴詵腔坌醞隊懊嬪賢隊拔舷露猿頻牧教跛摺W苤礁鮒本恫煌倉逭皇保湎喙嵯咴詵腔坌醞隊懊嬪賢隊拔擼沂竅蚪閑〉腦倉宸較虬枷蟯淝?
3投影畫法
通過數學推導,我們獲得:除相貫線為直線這種特殊情況外,其余兩正交圓柱體相貫線在非積聚性的投影面上投影均為雙曲線。對于兩正交圓柱體相貫線畫法可采用表面取點法去求作,求出相貫線上的特殊點,然后再根據需求求出一般點,最后用光滑的曲線連接各點即可。這好比已經知道了該問題的答案,只不過利用表面取點法這種方法來重演這個問題,抑或說求作方法更強調的是一種過程,這里估且不去討論表面取點法來求作相貫線的投影步驟。在現實設計中,圖紙上出現兩圓柱體的相貫線情況較多,兩圓柱軸線正交相貫且直徑不相等時,在不致引起誤解的情況下,通常是采用的簡化畫法來替代取點方法求作相貫線的投影,即以相貫兩圓柱體中較大圓柱的半徑為半徑,以圓弧替代相貫線。所以說兩正交圓柱體相貫線在實際操作中更注重的是最后制圖表達的效果。兩圓柱體相貫線求解流程圖如圖4所示。
圖4兩圓柱體相貫線求解流程圖
4小結
工程制圖圓柱體相貫線的教學中要求學生重點熟悉和掌握兩正交圓柱體相貫線投影規律和作圖方法。正確理解和化抽象為具體的思路在于要深度領會兩正交圓柱體相貫線的投影形狀特征。本文是以數學推導的方式建立了相貫線的投影方程,如此可強化學生的邏輯記憶,同時也具備更強的說服力。此外,通過三維模擬技術生動再現了兩正交圓柱體相貫線的演變趨勢,這對學生從理性再到感性認識度又再次強化,如此可以將兩正交圓柱體相貫線的形狀特征深刻地固化在大腦里,在后期遇到繪制兩正交圓柱體相貫線時便可快速地作出形狀預判,結合簡化畫法,在實際操作中將更為準確、方便。
基金項目:安徽理工大學校青年基金(編號:QN201317)
參考文獻
[1] 張文利.幾種典型相貫線的數學分析[J].鎮江高專學報,2003.16(4):55-57.
[2] 李富平,左宗義,馮開平.制圖課件“相貫線"的設計與圖形制作[J].集美大學學報(自然科學版),2001 (增刊):253-255.
[3] 毛文武.基于CAD三維造型的制圖課程教學改革與探索[J].機電技術,2011(6):166-168.
[4] 林四連.Pro/ENGINEER在《工程制圖》相貫線教學中的應用[J].黎明職業大學學報,2009(2):53-55.
[5] 汪正俊.工程制圖[M].北京:人民郵電出版社,2013.

