構(gòu)造平行線 等角圖中轉(zhuǎn)

姚璐

在同一平面內(nèi)，不相交的兩條直線稱為平行線.平行線是初中平面幾何最基本的，也是非常重要的圖形.平行線具有強(qiáng)大的轉(zhuǎn)移功能，在解題時如果能根據(jù)題目需要構(gòu)造平行線實(shí)現(xiàn)角的轉(zhuǎn)移，那么能使計算證明變得簡單、流暢.

構(gòu)造平行線實(shí)現(xiàn)角的轉(zhuǎn)移的依據(jù)是：兩直線平行，同位角相等；兩直線平行，內(nèi)錯角相等；兩直線平行，同旁內(nèi)角互補(bǔ).利用平行線的的性質(zhì)，可以把相關(guān)信息轉(zhuǎn)移，實(shí)現(xiàn)已知和未知之間的聯(lián)系，從而解決問題.

下面舉例談?wù)勅绾螛?gòu)造平行線實(shí)現(xiàn)“角”的轉(zhuǎn)移，供同學(xué)們參考.

例 觀察圖1～圖5.

（1）如圖1，若AB∥CD，∠B+∠D=∠BED，你能說明為什么嗎？

反之，若∠B+∠D=∠BED，直線AB與CD有什么位置關(guān)系？請說明理由；

（2）若將點(diǎn)E移至圖2所示位置，此時∠B、∠D、∠BED之間有什么關(guān)系？請說明理由；

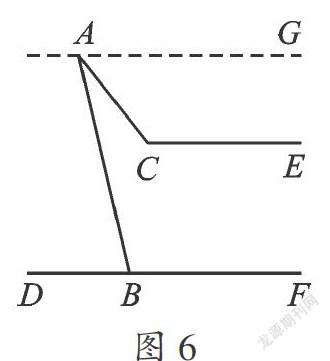
（3）若將E點(diǎn)移至圖3所示位置，情況又如何？

（4）如圖4，若AB∥CD，∠E+∠G與∠B+∠F+∠D又有何關(guān)系？

（5）如圖5，若AB∥CD，又得到什么結(jié)論？

【分析】要說明（1）的結(jié)論成立，難點(diǎn)是如何實(shí)現(xiàn)“和”，最直接的方法是將∠B、∠D轉(zhuǎn)移到一起，關(guān)鍵是如何實(shí)現(xiàn)角的轉(zhuǎn)移，就請平行線來幫忙吧.若過點(diǎn)E作EF∥AB，則由平行線的性質(zhì)即可說明；其余幾個問題也都可以按照此方法說明.

變式2 如圖7，已知直線AC∥BD，連接AB，直線AC、BD及線段AB把平面分成①、②、③、④四個部分，規(guī)定：線上各點(diǎn)不屬于任何部分.當(dāng)動點(diǎn)P落在某個部分時，連接PA、PB，構(gòu)成∠PAC、∠APB、∠PBD三個角.當(dāng)動點(diǎn)P在第③部分時，全面探究∠PAC、∠APB、∠PBD之間的關(guān)系，并寫出動點(diǎn)P的具體位置和相應(yīng)的結(jié)論.選擇其中一種結(jié)論加以證明.（提示：有公共端點(diǎn)的兩條重合的射線所組成的角是0°角）

【分析】分點(diǎn)P在射線BA的右側(cè)、在射線BA上、在射線BA的左側(cè)三種情況，過點(diǎn)P作平行線，構(gòu)造出內(nèi)錯角或同旁內(nèi)角實(shí)現(xiàn)角的轉(zhuǎn)移是解題的關(guān)鍵.

解：①當(dāng)動點(diǎn)P在射線BA的右側(cè)時（如圖8），結(jié)論是∠PBD=∠PAC+∠APB.

②當(dāng)動點(diǎn)P在射線BA上時（如圖9），結(jié)論是∠PBD=∠PAC+∠APB或∠PAC=∠PBD+∠APB或∠APB=0°，∠PAC=∠PBD（任寫一個即可）.

③當(dāng)動點(diǎn)P在射線BA的左側(cè)時（如圖10），結(jié)論是∠PAC=∠APB+∠PBD.