星圖識(shí)別的一種擴(kuò)充柵格算法

錢華明，孫 龍，蔡佳楠，黃 蔚

(哈爾濱工程大學(xué)自動(dòng)化學(xué)院，150001哈爾濱)

精確的姿態(tài)信息是航天器完成航天任務(wù)的基礎(chǔ).能夠提供姿態(tài)信息的測量器件有很多，但是精度最高應(yīng)用最廣泛的是星敏感器.星敏感器的姿態(tài)確定過程分星空成像、星點(diǎn)提取、星圖識(shí)別和姿態(tài)計(jì)算4個(gè)步驟.其中星圖識(shí)別是星敏感器姿態(tài)確定的決定性階段.對于星敏感器而言，星圖識(shí)別的實(shí)質(zhì)就是尋找觀測星圖中觀測星在導(dǎo)航星表中對應(yīng)的導(dǎo)航星［1］.

隨著星敏感器的發(fā)展，出現(xiàn)了許多的星圖識(shí)別算法.Padgett和Kreutz-Delgado等將星圖識(shí)別算法劃分為兩種類型［2］.第一種類型是子圖同構(gòu)類算法，這類算法把觀測星圖看成是全天星圖的子圖，將星點(diǎn)作為頂點(diǎn)，利用星點(diǎn)的星等和它們之間的角距等信息，以線段、三角形、多邊形等作為基本元素來進(jìn)行星圖識(shí)別［3］.其中最具代表性的有三角形算法［4］、匹配組算法［5］.另一種類型是模式識(shí)別類算法，這種算法為每顆星構(gòu)造一個(gè)獨(dú)一無二的特征“星模式”，這樣星圖識(shí)別的實(shí)質(zhì)就是在星表中尋找與觀測星模式相近的導(dǎo)航星.其中，比較有代表性的有柵格算法［2］、基于統(tǒng)計(jì)特征的識(shí)別算法［6］.

在這兩類算法中，三角形算法的應(yīng)用最廣泛.然而三角形算法容易受到噪聲的干擾，對噪聲的魯棒性較差，因此只能適用于噪聲水平較低的情況.文獻(xiàn)［7］針對各種噪聲對比了三角形算法、匹配組算法與柵格算法，結(jié)果表明柵格算法的噪聲魯棒性要遠(yuǎn)遠(yuǎn)高于三角形算法和匹配組算法.然而柵格算法要求視場中觀測星的數(shù)目不小于6顆［8］，這就限制了該算法在小視場、低星等敏感極限星敏感器中的應(yīng)用.文獻(xiàn)［9-10］中介紹了一種擴(kuò)充星圖的方法，利用陀螺的輸出和前一時(shí)刻的識(shí)別信息將星圖進(jìn)行擴(kuò)充，使得星圖中星點(diǎn)數(shù)目增加，從而達(dá)到算法要求的限度.然而擴(kuò)充星圖法在星圖識(shí)別階段采用的是三角形算法，因此無法擺脫三角形算法本身的缺陷，容易受到噪聲的影響.星敏感器本身存在著暗電流噪聲、畸變噪聲等，同時(shí)在航天器執(zhí)行任務(wù)時(shí)會(huì)不可避免地受到環(huán)境的影響從而引入一定的噪聲，在這種情況下，擴(kuò)充星圖算法的使用會(huì)受到很大的限制.

若將擴(kuò)充星圖的思想與柵格算法結(jié)合，利用擴(kuò)充星圖的方法來獲取更豐富的星點(diǎn)信息，利用柵格算法進(jìn)行星圖識(shí)別，既能夠打破柵格算法的限制，又可以利用柵格算法在星圖識(shí)別階段提高算法對噪聲的魯棒性，增加星圖識(shí)別成功率，這就是本文的擴(kuò)充柵格算法.與現(xiàn)有的擴(kuò)充星圖方法相比，擴(kuò)充柵格算法能夠繼承柵格算法優(yōu)勢，擁有更好的噪聲魯棒性，更加適用于噪聲水平較高的復(fù)雜環(huán)境.不管是擴(kuò)充星圖法還是本文的擴(kuò)充柵格法都用到了陀螺的輸出信息，因此擴(kuò)充星圖中必定存在由陀螺漂移引入的噪聲，研究這些噪聲對星圖識(shí)別的影響是十分必要的.這是原始擴(kuò)充星圖法中忽略的一項(xiàng)，在本文中對其進(jìn)行了詳細(xì)的分析并在仿真環(huán)節(jié)進(jìn)行了驗(yàn)證.

新算法用到了陀螺的輸出和前一時(shí)刻的識(shí)別結(jié)果，不屬于全天識(shí)別算法，文獻(xiàn)［11］將這種類型的算法命名為遞歸模式算法，這種模式的算法適用于星敏感器的跟蹤模式.因此，為了使得整個(gè)星圖識(shí)別過程完整地運(yùn)行，在初始姿態(tài)捕獲模式本文選用了Pyramid算法，這種算法解決了太空迷失問題(lost in space)，已經(jīng)被成功地應(yīng)用到實(shí)際飛行器中［12］.

1 算法描述

1.1 柵格算法

原始的柵格算法柵格圖像生成過程見圖1，具體執(zhí)行步驟［2，7］:1)從拍攝星圖中選取一顆星作為待識(shí)別星(參考星又叫主星)，然后將其連同其鄰域半徑pr一起移動(dòng)，使得其移動(dòng)到視場中央.2)決定近鄰星，近鄰星是在參考星鄰域半徑pr之內(nèi)，半徑br以外離參考星最近的星.3)以參考星和近鄰星連線為基準(zhǔn)，以主星為中心旋轉(zhuǎn)星圖，使得星圖的x軸穿過近鄰星.4)生成g×g柵格，得到一個(gè)有g(shù)2個(gè)元素的矢量，有伴星的網(wǎng)格為1，否則為0，從而得到一個(gè)參考星的星模式s=［a1a2…am］.

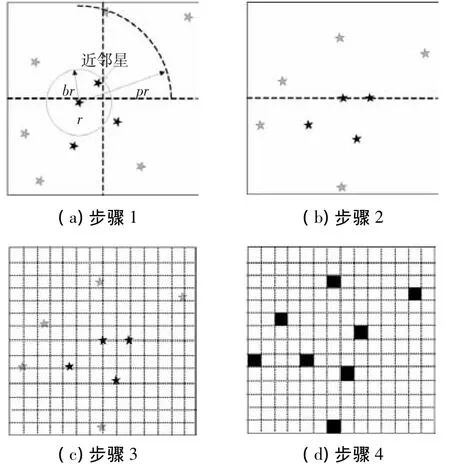
圖1 原始柵格算法

將參考星的星模式與存儲(chǔ)在數(shù)據(jù)庫中的星模式進(jìn)行對比，若與星庫中第i顆星的星模式的相同元素?cái)?shù)目超過門限值ξ，則認(rèn)為兩顆星匹配.若任意視軸下匹配星的數(shù)目超過兩顆，則認(rèn)為此次星圖識(shí)別成功.

從柵格的形成過程可以看出，近鄰星的緩沖半徑br和星圖某一坐標(biāo)軸方向上的柵格數(shù)目g控制柵格的形成過程，從而決定柵格算法的性能.若g較大，則每個(gè)柵格就較小，此時(shí)位置噪聲對算法的影響較大.但是g較大時(shí)能夠保證星圖中的星點(diǎn)充分被利用，使得一個(gè)是柵格中出現(xiàn)多顆星的概率降低，星模式有足夠多的維數(shù)進(jìn)行匹配.但是，如果g太大，柵格算法的計(jì)算量將會(huì)大大增加，更嚴(yán)重的是星點(diǎn)可能出現(xiàn)在多個(gè)柵格中，使得誤匹配的概率增加.反之g減小，則每個(gè)柵格將會(huì)變大，噪聲對算法的影響隨之減小.然而，當(dāng)g變小的時(shí)候，一個(gè)柵格中出現(xiàn)多顆星的概率將會(huì)升高.如果g過小，會(huì)使得星模式維數(shù)太低，達(dá)不到正常識(shí)別的要求.同理，br變大會(huì)使得算法對噪聲的魯棒性變強(qiáng)，但是br太大會(huì)使得近鄰星出現(xiàn)在視場之外的幾率增加，使得近鄰星的選擇成功率降低，這將會(huì)直接影響到算法的星圖識(shí)別成功率.因此，在小視場的星敏感器使用中，需要統(tǒng)計(jì)星點(diǎn)在視場中的分布情況，然后根據(jù)統(tǒng)計(jì)結(jié)果來設(shè)置柵格數(shù)目g和緩沖半徑br.

1.2 擴(kuò)充星圖法

在某些情況下為了滿足低功耗、小體積的條件，星敏感器的視場一般被設(shè)置得很小，Nano-JASMINE就是一個(gè)典型實(shí)例［13］.在這種情況下，不能保證每次都能捕獲到兩顆以上的恒星，因此星圖識(shí)別的過程就不能正常進(jìn)行，下面介紹一種利用擴(kuò)充星圖進(jìn)行星圖識(shí)別的方法［8-9］，具體步驟:1)t時(shí)刻星圖識(shí)別成功后，計(jì)算載體的姿態(tài)，利用姿態(tài)信息分析星圖中沒有被用來進(jìn)行星圖識(shí)別的星點(diǎn)，并記錄它們的位置.2)利用得到的姿態(tài)信息和陀螺輸出的測量信息估計(jì)t+1時(shí)刻步驟1中記錄的星點(diǎn)的位置，如果在t+1時(shí)刻星點(diǎn)位置不在預(yù)測星圖中，則按照圖2所示的擴(kuò)充星圖法將視場擴(kuò)充.3)當(dāng)星敏感器在t+1時(shí)刻得到拍攝星圖時(shí)，將其與步驟2預(yù)測星圖中的星利用三角形算法進(jìn)行識(shí)別，若識(shí)別成功的星點(diǎn)數(shù)目不小于2，利用識(shí)別成功的恒星計(jì)算載體姿態(tài)，否則跳到下一步.4)識(shí)別擴(kuò)充視場中的恒星，若失敗，則整個(gè)星圖識(shí)別失敗.

圖2 擴(kuò)充星圖法

1.3 擴(kuò)充柵格算法

上述擴(kuò)充星圖的方法，將星圖擴(kuò)充之后能夠得到更豐富的星點(diǎn)信息.這種方法實(shí)際上跟增大星敏感器視場起到的效果相同.因此為了更加的直觀，本文將其加以改變，變?yōu)閿U(kuò)充視場的方法，假設(shè)實(shí)際視場大小為θR×θR，擴(kuò)充后的視場大小為θE×θE，算法流程見圖3，算法步驟:1)t時(shí)刻星圖識(shí)別成功后，計(jì)算載體的姿態(tài).2)在t+1時(shí)刻利用得到的姿態(tài)和陀螺的輸出信息計(jì)算視軸的方向矢量P.利用P從星表中選擇落入視場θE×θE中的恒星，生成t+1時(shí)刻的模擬星圖A.此模擬星圖包括模擬真實(shí)星圖和擴(kuò)充星圖兩部分，如圖4所示.3)敏感器在t+1時(shí)刻拍攝到的為星圖B，將星圖A和B組合并刪除星圖A中真實(shí)模擬星圖中的星點(diǎn)，從而生成星圖C，如圖4所示.4)從星圖C中的真實(shí)視場中選擇待識(shí)別星，使用柵格算法進(jìn)行識(shí)別.

圖3 算法流程

圖4 擴(kuò)充柵格算法

從上述步驟可以看出，在星圖識(shí)別階段使用的是柵格算法，它的噪聲魯棒性要優(yōu)于現(xiàn)有擴(kuò)充星圖法中的三角形算法.同時(shí)通過將視場進(jìn)行擴(kuò)充可以得到更多的星點(diǎn)信息，從而達(dá)到柵格算法的要求.傳統(tǒng)柵格算法使用查找表進(jìn)行星模式的查找和匹配，在參考星表較大的情況下效果很好.但是擴(kuò)充柵格算法用于跟蹤模式，不需要建立參考星表，因此本文用圖5所示的方法構(gòu)造星模式:每一個(gè)柵格分配一個(gè)數(shù)字，最后記錄有伴星的柵格分配到的數(shù)字;將這些數(shù)字組成一個(gè)矢量，這個(gè)矢量就可以看作參考星的星模式.

圖5 星模式的構(gòu)造

2 陀螺噪聲分析

由于陀螺漂移的存在，使用陀螺信息生成的模擬星圖中必定引入了因陀螺漂移而產(chǎn)生的位置噪聲.研究該噪聲對星圖識(shí)別算法的影響是十分必要的.

為簡化計(jì)算，假設(shè)星敏感器與載體之間的安裝矩陣為單位陣且陀螺捷聯(lián)安裝在載體的三軸上.假設(shè)在t時(shí)刻，星點(diǎn)在像平面的位置為(xtc，.如圖 6 所示，ωx、ωy、ωz分別為載體三軸的轉(zhuǎn)動(dòng)角速度，由ωy引起的星點(diǎn)移動(dòng)速度為v1且沿x軸反方向;由ωx引起的星點(diǎn)移動(dòng)速度為v2且沿y軸方向;由ωz引起的移動(dòng)速度可分解為沿著x軸的負(fù)方向速度v3和沿著y軸的正方向速度v4.則星點(diǎn)的移動(dòng)速度可以表示為［14］

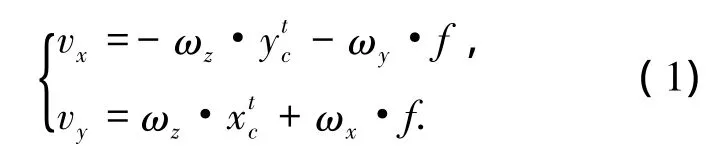
式中:f為星敏感器光學(xué)系統(tǒng)的焦距.

根據(jù)式(1)可以得到t+δt時(shí)刻星點(diǎn)的位置為

當(dāng)δt較小時(shí)，有

陀螺的測量模型可以簡化為ω=ωr+b+η，其中ωr為真實(shí)角速度;b為陀螺常值漂移;η為陀螺隨機(jī)測量噪聲，將其代入上式，則得

則由陀螺測量噪聲引起的星點(diǎn)位置誤差為

假設(shè)3個(gè)陀螺相同，bx+ηx=by+ηy=bz+ηz=b+η，那么由陀螺測量噪聲引入的總的星點(diǎn)位置誤差為

假設(shè)星敏感器誤差引起的星點(diǎn)位置噪聲為δps像素.若新方法在星點(diǎn)位置噪聲為δp+δps時(shí)仍能保證較高的星圖識(shí)別成功率，則能夠說明新算法對陀螺噪聲有較強(qiáng)的魯棒性.

圖6 星點(diǎn)移動(dòng)示意

3 仿真與分析

仿真中所用的基本星表是第谷第二星表(Tycho-2)，從中選取星等亮度大于 8.0的星42 057顆組成導(dǎo)航星表.

由于各種噪聲的存在，星敏感器不能夠完美地呈現(xiàn)星空.因此，為了模擬真實(shí)情況下的星圖識(shí)別過程，用兩種形式的高斯白噪聲對所有的噪聲進(jìn)行模擬.第 1種是星等噪聲 MN(magnitude noise)，由恒星亮度的變化引起.第2種是星點(diǎn)的位置噪聲PN(position noise)，由星敏感器噪聲和陀螺測量噪聲引起，測量單位為像素.另外，由于恒星的自行、測量誤差等因素的存在，星表中也存在噪聲.對于大視場星敏感器而言，與其他噪聲相比星表噪聲非常小，可以忽略不計(jì).然而，對于本文使用的小視場星敏感器，星表噪聲是需要考慮的一個(gè)因素，因此在本文中星表噪聲也用MN和PN來表征.圖7、8分別描述了星敏感器拍攝星圖和擴(kuò)充法中用到的模擬星圖的模擬方法.

圖7 拍攝星圖的模擬方法

圖8 模擬星圖的模擬方法

3.1 仿真條件設(shè)置

根據(jù)1.1節(jié)的敘述，需要根據(jù)星點(diǎn)在星圖中分布的統(tǒng)計(jì)結(jié)果來設(shè)置柵格數(shù)目g和緩沖半徑br.選取星敏感器視場大小為4°×4°，星等敏感極限為7.5，圖9為10 000次隨機(jī)視軸指向星點(diǎn)之間角距分布的統(tǒng)計(jì)結(jié)果.

圖9 視場中星點(diǎn)角距分布統(tǒng)計(jì)

根據(jù)統(tǒng)計(jì)結(jié)果，星點(diǎn)之間的角距在0～0.1°之間的概率為 0.17%，在 0.1～0.2°之間的概率為0.67%，在 0.2～0.3°之間的概率為 1.02%.則角距分布在 0～0.2°之間的概率為 0.17%+0.67%=0.84%，因此選取柵格大小為0.2°.選取擴(kuò)充視場大小為 8°×8°，像平面像素為 1 024×1 024，則柵格數(shù)目g=8°/0.2°=40.同理選擇緩沖半徑br=0.3°，約為40像素.其他仿真參數(shù)設(shè)置:星表星等噪聲為0.1像素，位置噪聲為0.1像素，陀螺常值漂移為 1°/h，隨機(jī)漂移為 0.5°/h.

3.2 仿真結(jié)果

本文的仿真中分為兩個(gè)部分，第1部分是在不同噪聲環(huán)境下本文的擴(kuò)充柵格算法與現(xiàn)有的擴(kuò)充星圖法的對比，第2部分是算法性能的全面驗(yàn)證.

圖10為星敏感器星等噪聲為0.2像素時(shí)擴(kuò)充柵格算法和擴(kuò)充星圖法的星圖識(shí)別成功率隨著位置噪聲變化的曲線.

圖10 識(shí)別成功率隨位置噪聲變化曲線

圖11為位置噪聲為0.3像素時(shí)擴(kuò)充柵格算法和擴(kuò)充星圖法的星圖識(shí)別成功率隨著星等噪聲變化的曲線.

圖11 識(shí)別成功率隨星等噪聲變化曲線

由圖10、11可見，隨著星等噪聲和位置噪聲的增加，現(xiàn)有的擴(kuò)充星圖法由于在星圖識(shí)別階段用的是三角形算法，所以其噪聲魯棒性較差，導(dǎo)致星圖識(shí)別成功率迅速降低.而由于擴(kuò)充柵格法用的是魯棒性較強(qiáng)的柵格算法，其識(shí)別成功率明顯優(yōu)于擴(kuò)充星圖法.

下面對擴(kuò)充柵格算法的性能進(jìn)行全面的驗(yàn)證，一般用如下3項(xiàng)指標(biāo)評(píng)價(jià)星圖識(shí)別算法的性能:1)算法在不同噪聲環(huán)境下的星圖識(shí)別成功率.2)算法平均進(jìn)行一次成功識(shí)別所用的時(shí)間.3)算法數(shù)據(jù)庫對內(nèi)存的要求.

隨著微電子技術(shù)的發(fā)展，大容量小體積的存儲(chǔ)器件不斷出現(xiàn)，內(nèi)存的需求對星圖別算法的限制越來越小，因此本文不考慮這方面的因素.由于新算法用到了陀螺信息，由式(6)可知星敏感器的更新周期會(huì)影響陀螺引入的位置噪聲.因此本文添加一項(xiàng)星敏感器更新周期對算法識(shí)別成功率的影響.首先，當(dāng)星敏感器更新周期為1 s時(shí)，在10 000次隨機(jī)視軸的仿真中，新算法星圖識(shí)別成功率與位置噪聲標(biāo)準(zhǔn)偏差之間的關(guān)系曲線見圖12.

圖12 星圖識(shí)別成功率

由圖12可見，當(dāng)位置噪聲小于1像素時(shí)，新算法的星圖識(shí)別成功率大于97.4%.同時(shí)還注意到一點(diǎn)，當(dāng)位置噪聲為0時(shí)，星圖識(shí)別成功率也達(dá)不到100%.因?yàn)橛袝r(shí)星敏感器只能捕獲到一顆或者兩顆星，這時(shí)成功識(shí)別兩顆星的概率會(huì)大大降低.在上述仿真條件下，10 000次隨機(jī)視軸仿真中，星敏感器捕獲星數(shù)目的統(tǒng)計(jì)結(jié)果見表1和圖13.星敏感器捕獲到小于兩顆星的概率為0.6%，而星圖識(shí)別過程成功的要求是至少成功匹配兩顆星.因此即使所有誤差都不存在，星圖識(shí)別的成功率也只有99.4%.但是，這并不能代表本文的算法不夠優(yōu)秀，從表中可以發(fā)現(xiàn)，星敏感器捕獲不小于6顆星的概率為79.71%，即傳統(tǒng)算法即使在所有噪聲都為零時(shí)，星圖識(shí)別成功率也只能達(dá)到79.71%，而本文算法在位置噪聲為1像素的情況下仍能夠達(dá)到97.4%.能夠取得這么高的成功率，除了視場擴(kuò)充帶來更豐富的星點(diǎn)信息之外，近鄰星選擇成功率的提高也是一個(gè)很重要的因素.傳統(tǒng)方法近鄰星的選擇成功率最高只有52.2%，而本文算法近鄰星成功率最大可達(dá)到86.7%，如圖14所示.主要原因是，新算法的參考星是從真實(shí)星圖中選擇，而真實(shí)星圖在整個(gè)擴(kuò)充后的星圖的中央，因此參考星的近鄰星不會(huì)出現(xiàn)在擴(kuò)充后星圖的邊緣，使得近鄰星出現(xiàn)在星圖外的概率大大降低.

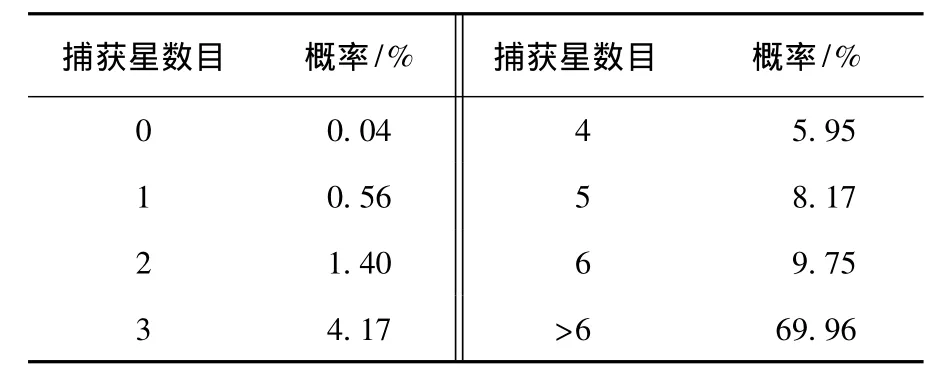
表1 星敏感器捕獲星數(shù)目統(tǒng)計(jì)

圖13 星敏感器捕獲星數(shù)目的統(tǒng)計(jì)概率

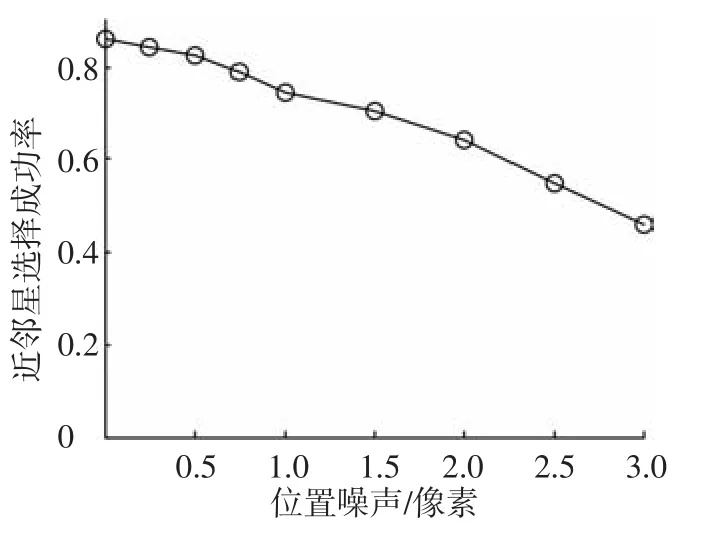
圖14 新算法近鄰星選擇成功率

假設(shè)星敏感器的更新周期為t，圖15為當(dāng)星敏感器的位置噪聲為0.3像素時(shí)，更新周期與星圖識(shí)別成功率的仿真結(jié)果.圖16為由陀螺漂移引入的位置噪聲隨更新周期變化的仿真結(jié)果.

圖15 更新周期對星圖識(shí)別成功率的影響

圖16 陀螺引入的位置噪聲與更新周期的關(guān)系曲線

由15、16可見，當(dāng)星敏感器更新周期為10 s時(shí)，由陀螺漂移引入的位置噪聲約為0.54像素，此時(shí)總的位置噪聲為0.84像素，星圖識(shí)別成功率為97.6%.而實(shí)際上星敏感器的更新頻率為1～10 Hz，即其更新周期小于1 s，因此由陀螺引入的位置噪聲小于0.05像素，這時(shí)總的位置噪聲小于0.35像素，星圖識(shí)別成功率達(dá)到98.2%.因此，考慮到柵格算法對噪聲的強(qiáng)魯棒性，由陀螺漂移產(chǎn)生的噪聲對星圖識(shí)別成功率的影響非常小，可以不予考慮.

圖17為星敏感器捕獲星數(shù)目與進(jìn)行一個(gè)星圖識(shí)別的平均識(shí)別時(shí)間之間的關(guān)系.仿真硬件:Pentium(R)CPU E5200，2.49 GHz，計(jì)算機(jī)系統(tǒng)為Windows XP，所用軟件為 MATLAB，代碼沒有經(jīng)過優(yōu)化.由圖中看出，隨著捕獲星數(shù)目的增加，星圖識(shí)別所用時(shí)間也隨之增加.但是由于小視場星敏感器一次只能捕獲幾顆星，因此平均識(shí)別時(shí)間大約為6 ms.

圖17 新方法耗時(shí)

另外，本文還將新方法應(yīng)用于低星等敏感極限的星敏感器時(shí)，進(jìn)行仿真，得到了相似的實(shí)驗(yàn)結(jié)果.綜上所述，擴(kuò)充柵格算法的噪聲魯棒性要優(yōu)于現(xiàn)有擴(kuò)充星圖法，同時(shí)能夠?qū)⒁晥鲞M(jìn)行擴(kuò)充，得到足夠的星點(diǎn)信息來進(jìn)行星圖識(shí)別，且在復(fù)雜噪聲環(huán)境中能夠達(dá)到很高的識(shí)別成功率，是一種適用于小視場或低星等敏感極限的星敏感器的星圖識(shí)別算法.

4 結(jié) 論

1)提出了一種適用于小視場或低星等敏感極限星敏感器的擴(kuò)充柵格算法.該算法是基于傳統(tǒng)高魯棒性的柵格算法而建立的，相較于現(xiàn)有擴(kuò)充星圖法擁有更強(qiáng)的噪聲魯棒性.同時(shí)新算法可以通過擴(kuò)充視場來獲得更多的星點(diǎn)信息，能夠打破原始柵格算法的限制.

2)實(shí)驗(yàn)結(jié)果表明，在星敏感器為小視場或者低星等敏感極限時(shí)，擴(kuò)充柵格法的星圖識(shí)別成功率優(yōu)于傳統(tǒng)的擴(kuò)充星圖法.擴(kuò)充柵格法的近鄰星識(shí)別成功率優(yōu)于傳統(tǒng)的柵格算法.綜合上述優(yōu)勢，該擴(kuò)充柵格算法在小視場星、低星等敏感極限星敏感器上體現(xiàn)出了較好的技術(shù)性能.

［1］LIEBE C C.Star trackers for attitude determination［J］.IEEE Trans on Aerospace and Electronic System，1995，10(6):10-16.

［2］PADGETT C，KREUTZ-DELGADO K.A grid algorithm for autonomous star identification［J］.IEEE Trans on Aerospace and Electronic System，1997，33(1):202-213.

［3］張廣軍.星圖識(shí)別［M］.北京:國防工業(yè)出版社，2011:22-29.

［4］COLE C L.Fast star pattern recognition using spherical triangles［D］.Buffalo，NY:State University of New York at Buffalo，2004.

［5］KOSIK J.Star pattern identification aboard an inertially stabilized spacecraft［J］.Journal of Guidance，Control and Dynamics，1991，14(1):230-235.

［6］ UDOMKESMALEE S，ALEXANDER J，TOLIVAR F.Stochastic star identification ［J］.Journal of Guidance，Control and Dynamics，1994，17(6):1283-1286.

［7］PADGETT C，KREUTZ-DELGADO K，UDOMKESMALEE S.Evaluation of star identification techniques［J］.Journal of Guidance，Control and Dynamics，1997，20(2)，259-267.

［8］HO K.A survey of algorithms for star identification with low-cost star trackers ［J］.Acta Astronautica，2012，73:156-163.

［9］Compact and low-cost advanced star sensor system［R］.Tokyo，Japan:Mitsubishi Electric and Electronics，2002:1-12.

［10］HO K，NAKASUKA S.Novel star identification method combining two star trackers with extended FOVs［C］//AIAA Guidance，Navigation，and Control Conference.Toronto，Ontario，Canada:IEEE，2010:1-15.

［11］SAMAAN M A，MORTARI D，JUNKINS J L.Recursive mode star identification algorithms［J］.IEEE Trans on Aerospace and Electronic System，2005，41(4):1246-1254.

［12］MORTARI D，JUNKINS L J，SAMAAN M A.Lost-inspace pyramid algorithm for robust star pattern recognition［C］//Proceeding of Guidance and Control 2001.Colorado:Elsevier，2001:1-23.

［13］Scholarpedia.Nano-JASMINE［EB/OL］.http://www.space.t.u-tokyo.ac.jp/nanojasmine/Index-e.htm.

［14］XING Fei，CHEN Nan，YOU Zheng，et al.A novel approach based on MEMS-Gyro’s data deep coupling for determining the centroid of star spot［J］.Mathematical Problems in Engineering，2012，2012:403584.