斷續電流型開關電感Buck-Boost變換器的分岔現象

孫立山，楊 爽，劉洪臣

(哈爾濱工業大學電氣工程及自動化學院，150001哈爾濱)

DC-DC變換器屬于強非線性系統，當電路參數發生變化時，系統將產生分岔現象并最終進入混沌狀態，從而導致系統的運行狀態無法預測，甚至造成系統故障.因此，深入研究DC-DC變換器的非線性行為，分析電路參數對系統動態特性的影響，對于開關變換器系統的設計具有十分重要的理論意義和應用價值.

開關電感結構是近年來提出的一種新型拓撲，具有升壓模式和降壓模式兩種結構，可以分別嵌入到傳統DC-DC變換器中，以提高系統的升壓或降壓能力［1-2］，因而得到國內外學者的廣泛關注.

目前，國內外學者對傳統DC-DC變換器中非線性行為的研究已經比較深入［3-15］，人們利用數值模擬和非線性動力學理論等方法，深入分析了系統的分岔和混沌現象.以Buck-Boost變換器為例:文獻［13-15］證實了傳統Buck-Boost變換器中存在邊界碰撞分岔、倍周期分岔和陣發混沌等多種復雜的非線性動力學行為.然而，上述成果的研究對象均為傳統Buck-Boost變換器，而對基于開關電感結構的Buck-Boost變換器(下面簡稱開關電感Buck-Boost變換器)中非線性行為的研究結果卻未見報道.并且目前對于DC-DC變換器中非線性現象的研究主要集中于連續電流模式(CCM)，對斷續電流模式(DCM)的情況則研究較少.實際上，對DCM模式下系統的非線性動力學行為進行研究具有更為廣泛的意義.

因此，本文首次以開關電感Buck-Boost變換器為研究對象，深入分析了系統在DCM模式下的分岔和混沌現象.首先，從狀態方程出發，建立了DCM模式下系統的離散時間映射模型，并基于此模型，繪制了不同參數范圍內系統的分岔圖，分析了電路參數對系統動態特性的影響;然后，采用Runge-Kutta算法直接對狀態方程進行求解，得到了系統的龐加萊截面，更加直觀地反映了系統的運行狀態;接下來，根據系統不動點鄰域內Jacobian矩陣特征值的變化趨勢確定系統首次分岔點的位置;最后，應用PSIM軟件搭建符合實際運行條件的仿真模型，通過時域波形圖和相軌圖觀察變換器豐富的動力學演化過程，驗證了離散時間模型的正確性.

1 變換器的工作原理與建模

1.1 工作原理與狀態方程的求解

開關電感Buck-Boost變換器是運用開關電感結構代替傳統Buck-Boost變換器中原有的儲能電感而形成的，電流模式控制下系統的電路原理圖如圖1所示.由圖1可知，該系統是由兩個電感和一個電容組成的三階電路.電路的工作原理如下:將電感L1的電流iL1與參考電流Ⅰref比較的結果作為RS觸發器R端的輸入，時鐘信號通過觸發器的S端輸入，觸發器的Q端控制開關管S的通斷.當變換器工作于DCM模式時，電路有以下3種模態，如圖2所示.

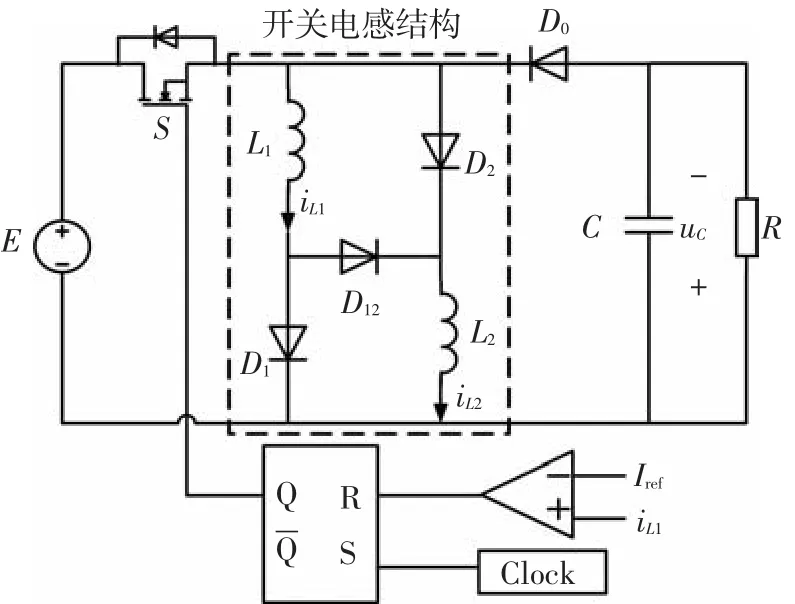
圖1 電流模式控制下的開關電感Buck-Boost變換器

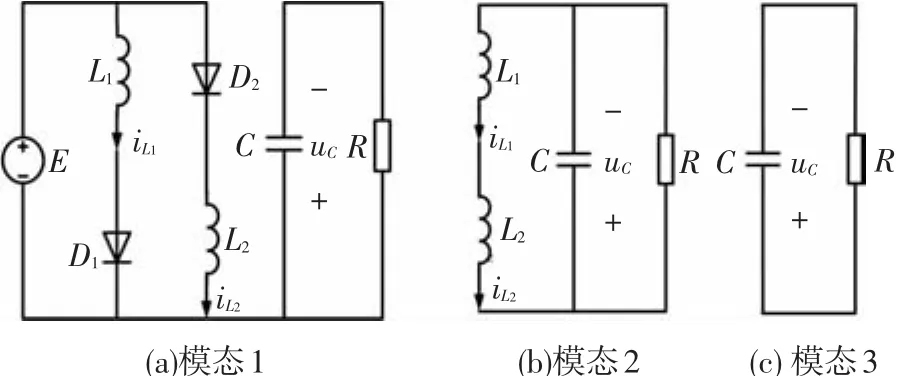
圖2 DCM運行時的模態

模態1.開關管S導通，二極管D0、D12截止，D1、D2導通，電感L1、L2并聯充電，電容C向負載提供能量，其等效電路如圖2(a)所示，此時有

模態2.開關管S截止，二極管D0、D12導通，D1、D2截止，電感L1、L2串聯為電容C充電，并向負載提供能量，其等效電路如圖2(b)所示，此時有

模態 3.開關管S、二極管D0、D1、D2、D12均截止，只有電容C向負載提供能量，其等效電路如圖2(c)所示，此時有

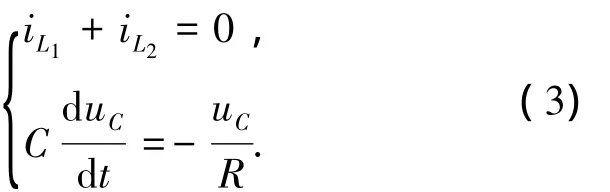
為便于分析，本文取L1=L2，則在上述3種模態中，可近似認為iL1=iL2，系統可簡化為二階模型，以電感電流iL1和電容電壓uC為分析對象，則對于模態1，有

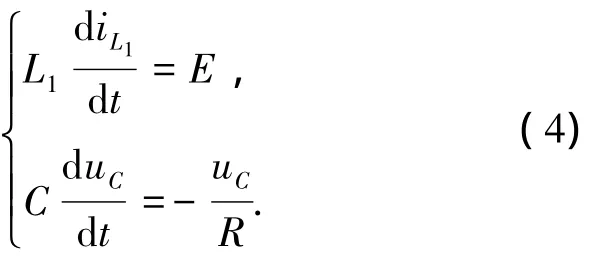
設電感電流iL1和電容電壓uC的初值分別為iL1，n和uC，n，則上述方程的時域解為

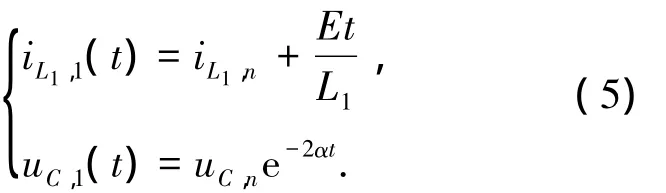
設變換器工作于模態1的時間為t1，則由式(5)得

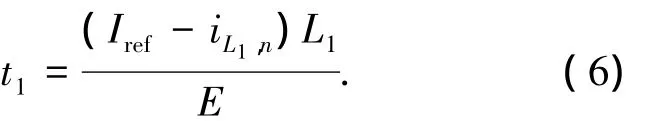
同理，模態2的微分方程可以簡化為

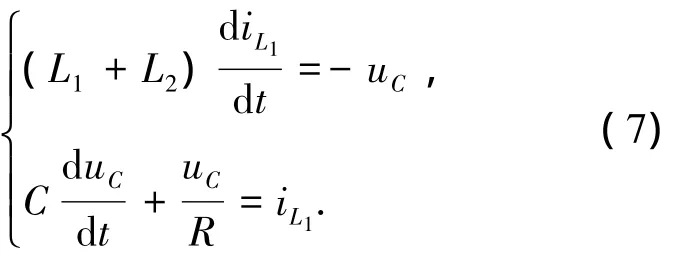
由式(5)可以解得

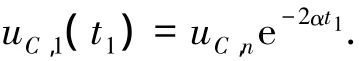
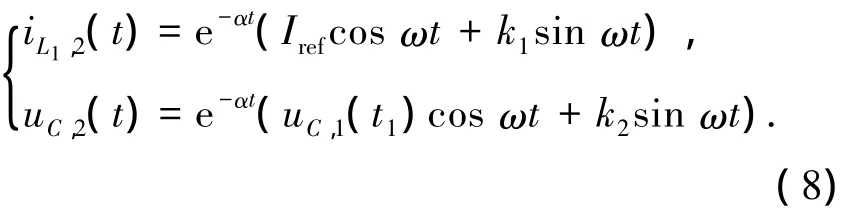
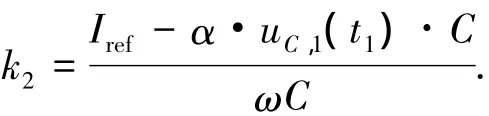
設變換器工作于模態 2的時間為t2，則iL1，2(t2)=0，由(8)式可得

當變換器工作于模態3時，簡化的微分方程為

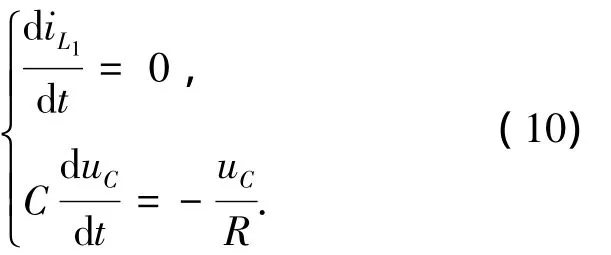
狀態方程(10)的解可表示為

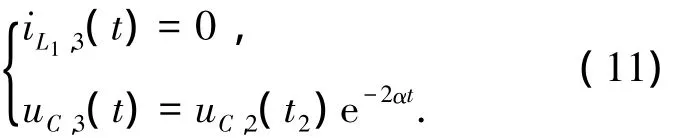
其中:uC，2(t2)=e-αt2(uC，1(t1)cos ωt2+k2sin ωt2)．

1.2 離散時間映射模型

本文采用頻閃映射的方法，設數據采樣周期為T，則在相鄰的采樣時刻內，DCM模式下的開關電感Buck-Boost變換器有以下3種運行軌道.

當t1≥T時，在1個采樣周期內，變換器只工作于模態1，則在第n個采樣周期結束時，簡化的微分方程對應的離散映射模型為

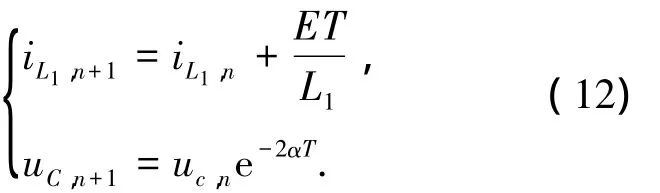
當t1＜T，但t1+t2≥T時，在1個采樣周期內，變換器工作于模態1和模態2，則在第n個采樣周期結束時，簡化的微分方程對應的離散映射模型為

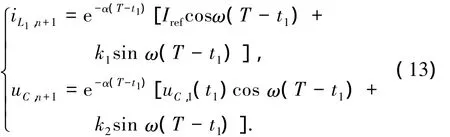
當t1＜T，且t1+t2＜T時，在1個采樣周期內，變換器工作于3種工作模態，則在第n個采樣周期結束時，簡化的微分方程對應的離散映射模型為

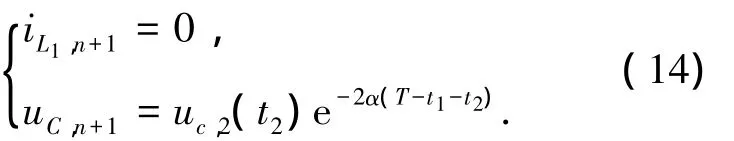
式(12)～(14)即為DCM模式下，開關電感Buck-Boost變換器的離散時間映射模型.

2 變換器的動力學行為分析

2.1 分岔圖

在動力學系統中，當系統參數的變化超過某臨界值時，系統的定性形態會突然發生變化，這種現象叫做分岔，臨界值即為分岔點.通過分岔圖可以清楚地知道系統在不同參數下的穩定性，因此，分岔理論是研究系統穩定性的有力工具.

在繪制分岔圖前，首先給出電感電流邊界的定義.當開關電感Buck-Boost變換器工作于DCM模式時，在狀態空間中存在兩個電流邊界，設第1個電流邊界為Ⅰb1，它滿足如下關系:以Ⅰb1為電流初值，經1個開關周期T后電感電流iL1恰好到達參考電流Ⅰref;設第2個電流邊界為Ⅰb2，它滿足:以Ⅰb2為電流初值，經1個開關周期T后電感電流iL1恰好為0，則此階段電感電流iL1到達參考電流Ⅰref的時間為T-t2，則由式(5)可知，DCM模式下開關電感Buck-Boost變換器的兩個電感電流邊界可分別表示為

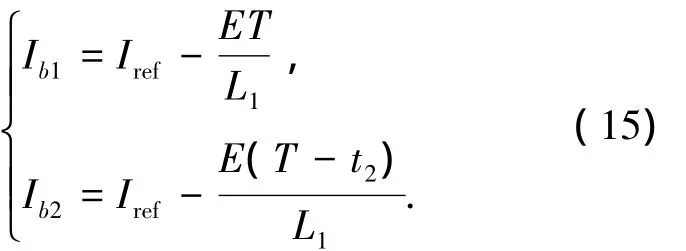
選取電路參數為C=10 μF，R=10 Ω，T=100 μs和L1=L2=0.1 mH，固定E=6 V，以參考電流Ⅰref為分岔參數，基于1.2節所導出的離散映射模型，對系統進行數值模擬，得到電感iL1隨參考電流變化的分岔圖，如圖3所示，其中紅色的點劃線表示第1個電感電流邊界Ⅰb1，綠色的點劃線表示第2個電感電流邊界Ⅰb2．由圖3可知，當參考電流Ⅰref達到2.5 A左右時，分岔軌線與邊界Ⅰb2發生碰撞，系統的工作狀態由周期1經邊界碰撞分岔變為周期2，隨著參考電流的進一步增大，電感電流并非完全工作在不連續狀態，而是在某些時鐘周期內有不連續現象;當Ⅰref為7.5 A左右時，系統再次發生邊界碰撞分岔變為周期4，而后激變進入混沌狀態．然而，這個混沌狀態并沒有被保持，當Ⅰref＞9.5 A時，混沌態和周期態交替出現，系統發生了DCM陣發混沌，陣發混沌前的分岔為切分岔.

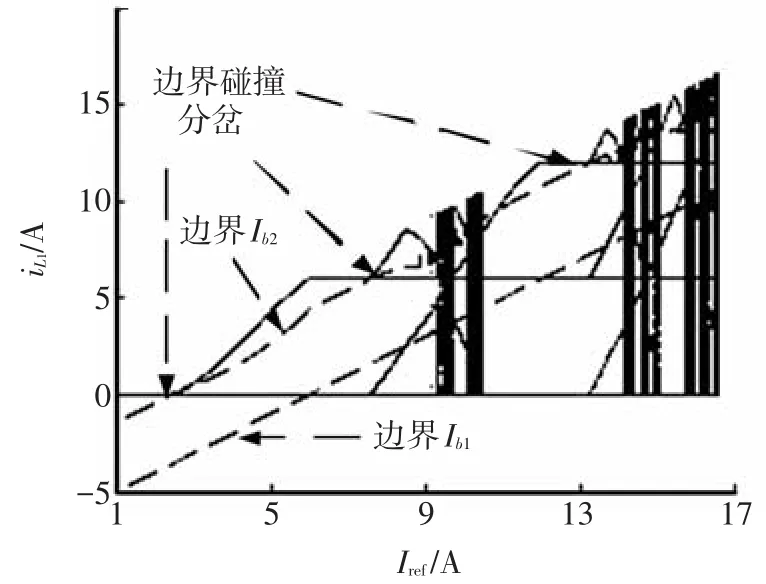
圖3 Ⅰref為參數的分岔

固定Ⅰref=2 A，其他電路參數與前者相同，以輸入電壓E為分岔參數，通過數值模擬得到的分岔圖如圖4所示．由圖4可知，隨著輸入電壓E的減小，系統的工作狀態也是由周期1經邊界碰撞分岔變為周期2，再到周期4，然后進入DCM陣發混沌區，并存在明顯的周期窗口.可見，其通往混沌的道路與參考電流變化時相同，但參數變化的方向相反.

值得注意的是，邊界碰撞分岔雖然也能引發倍周期現象，但與倍周期分岔有本質的區別.發生倍周期分岔時，分岔點附近的倍周期軌道與分岔發生之前的周期軌道是近似垂直的;而在邊界碰撞分岔中，二者并不垂直.并且由圖3和圖4還可以看出，當變換器工作于DCM模式時，引發系統不穩定的因素主要是電流邊界Ⅰb2，當系統軌線與Ⅰb2發生碰撞時，隨即產生分岔現象，并最終進入混沌狀態;然而，當系統軌線與Ⅰb1發生碰撞時，并未出現分岔，而僅僅改變了軌線的路徑，故Ⅰb1對系統的穩定性影響相對較小．

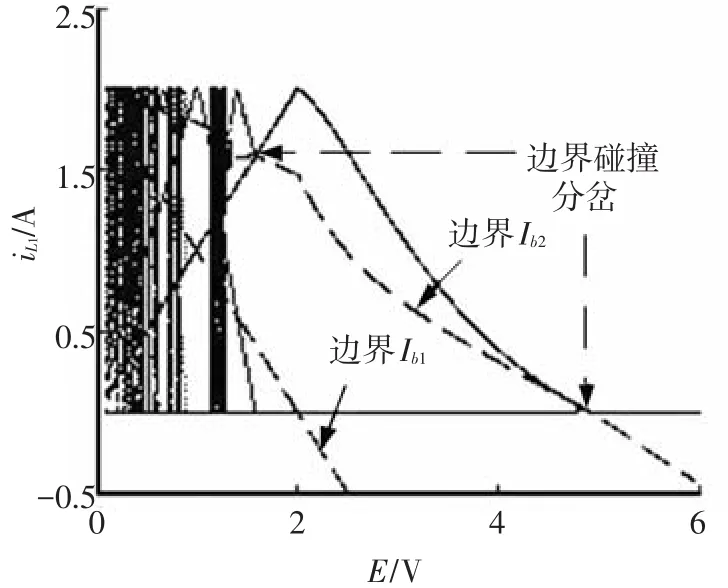
圖4 E為參數的分岔

2.2 龐加萊截面

在相空間中選取1個既不與軌線相切，又不包含軌線的截面，即龐加萊截面，軌線與龐加萊截面的交點稱為截點.由非線性動力學理論可知，通過觀察截點的情況便可以判斷是否發生混沌:當截面上只有1個點或少數離散點時，運動是周期的，點的個數代表狀態的周期數;當截點形成1條閉合的曲線時，運動是準周期的;當截點連成片或具有分形結構時，系統便處于混沌狀態.

為證明隨著參考電流Ⅰref的增大，變換器確實存在圖3分岔圖所體現的豐富的非線性行為，本節從不同工作模態下的狀態方程出發，采用Runge-Kutta算法直接對每個開關周期內的微分方程進行求解，得到開關電感Buck-Boost變換器在典型參考電流值下的龐加萊截面，其結果如圖5所示.

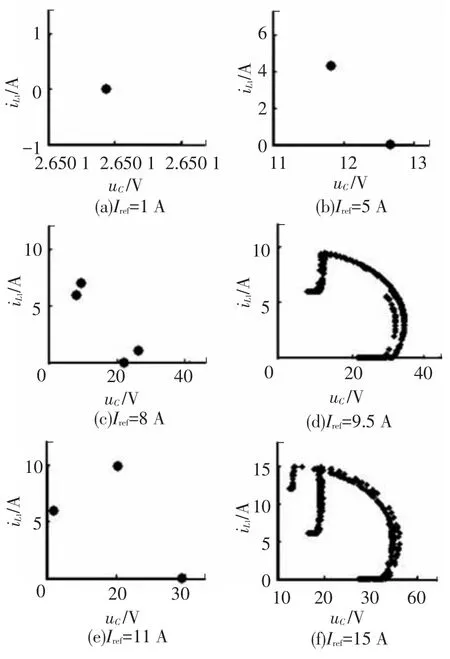
圖5 不同參考電流下的龐加萊截面

由圖5(a)～5(c)可以清楚的知道，當參考電流分別為1、5、8 A時，龐加萊截面上的點是離散的，根據點的個數可知，變換器先后工作于周期1、周期2和周期4;圖5(d)和5(f)中的截點在某些區域已經連成片，說明當參考電流為9.5、15 A時，變換器工作于混沌狀態;圖5(e)體現了當參考電流為11 A時，即在陣發混沌中，存在明顯的周期3窗口.上述結果與圖3所示分岔圖中各點呈現的狀態一致，驗證了離散映射模型的正確性，并且更加直觀地反映了參考電流取不同值時變換器所處的工作狀態.

3 基于離散時間模型的穩定性分析

3.1 不動點及Jacobian矩陣

令xn+1=xn=x*可求出系統的不動點x*，開關電感Buck-Boost變換器基于簡化狀態方程的離散時間模型在不動點鄰域內的Jacobian矩陣可表示為

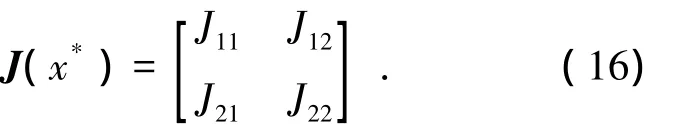
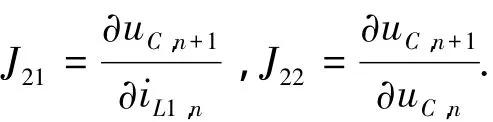
式(16)的特征方程為

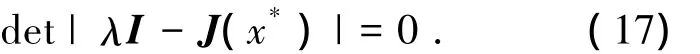
根據1.2節可知，在相鄰的采樣時刻nT和(n+1)T內，DCM模式下的開關電感Buck-Boost變換器有3種運行軌道，可分別對其穩定性進行分析.

當t1≥T時，式(12)所表示的離散系統不存在不動點，其Jacobian矩陣的元素分別為

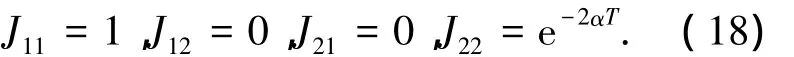
其特征多項式為

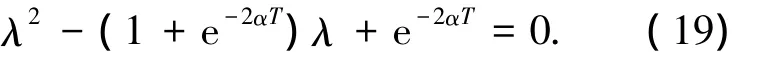
解得 λ1=1，λ2=e-2αT，此時離散系統Jacobian矩陣的特征值有兩個正實根，并且其中一個為1.

當t1＜T，但t1+t2≥T時，將xn+1=xn=x*代入式(13)，可求得系統的不動點，且由式(13)可求得其Jacobian矩陣的元素分別為

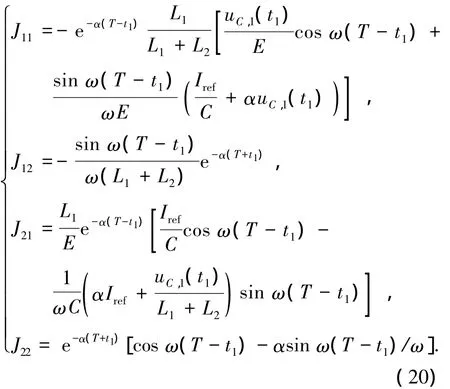
其特征多項式為

解得

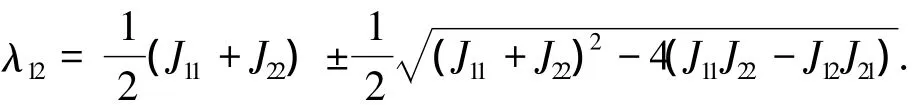
此時離散系統的Jacobian矩陣有兩個非零特征根.

當t1＜T，且t1+t2＜T時，式(14)所表示的離散系統僅存在1個不動點，由式(14)求得其Jacobian矩陣的元素分別為

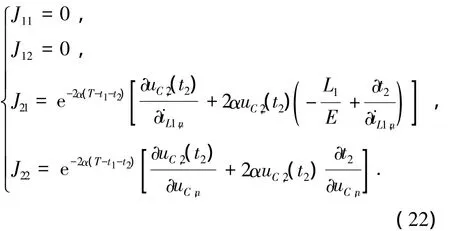
其中:

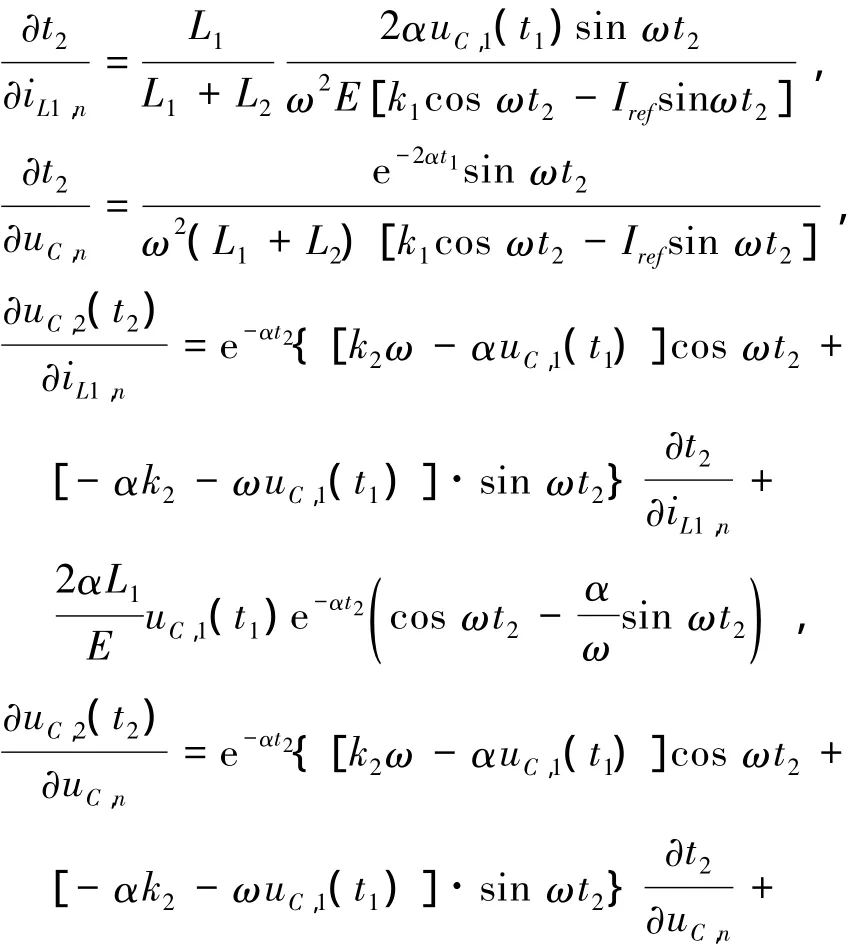
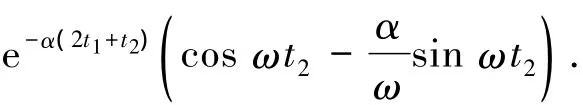
其特征多項式為

解得 λ1=J22，λ2=0，此時離散系統的Jacobian矩陣總有1個零特征根和1個非零特征根.

3.2 Jacobian矩陣的特征乘子

根據以上分析，本節計算了發生分岔前后離散映射模型在不動點鄰域內的Jacobian矩陣的特征值.表1、2分別給出了不同參考電流和不同輸入電壓下系統Jacobian矩陣特征值的變化情況.由表1可知，參考電流在(2.44 A，2.505 A)時，隨著參考電流的增大，周期1軌道的特征值由(-0.022 6，0)躍變為(-1.003 8，0.173 0).由表2可知，輸入電壓在(4.8 V，4.95 V)時，隨著輸入電壓的減小，周期1軌道的特征值由(-0.026 6，0)躍變為(-1.000 1，0.172 5).由此可知，系統發生了邊界碰撞分岔，且首次分岔的位置分別在Ⅰref=2.505 A和E=4.8 V處，這與圖3、4所示的分岔圖結果相一致.

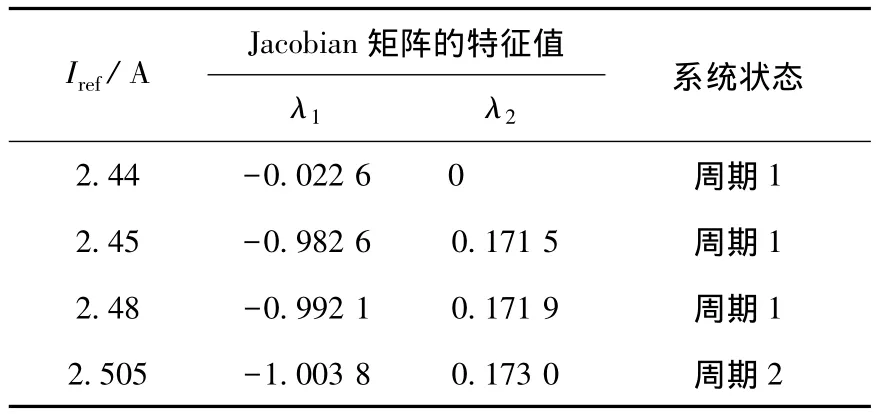
表1 不同參考電流下系統Jacobian矩陣的特征值

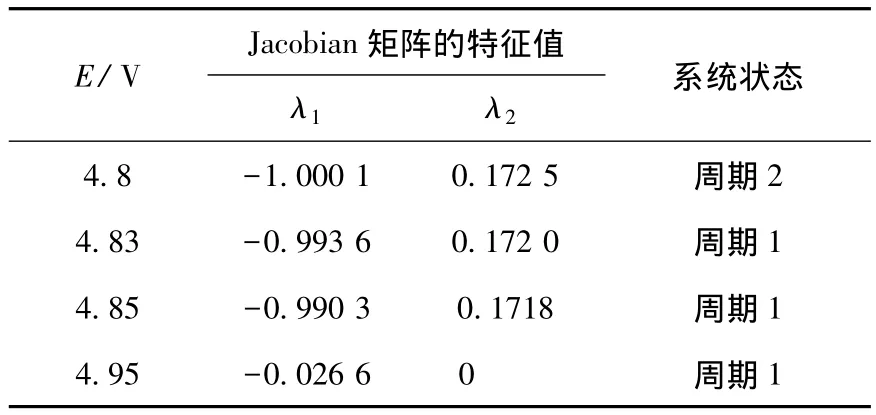
表2 不同輸入電壓下系統Jacobian矩陣的特征值

4 PSIM驗證

PSIM軟件是一款針對電力電子和電機控制的仿真軟件［13］，因仿真速度快、操作簡單而得到了廣泛的應用.為進一步驗證離散模型的正確性，本章根據圖1所示原理圖，在PSIM軟件中搭建了系統的仿真模型.選取參考電流Ⅰref為變量，其他電路參數與繪制圖3所示分岔圖時所選取的參數一致，典型參考電流值下的仿真結果如圖6～9所示.

由圖6～8可知，當參考電流分別為1、5、8 A時，變換器分別工作于周期1、周期2和周期4，時域波形表現為相應的周期性，相軌圖則由有限個數的封閉曲線組成，且由iL1的時域波形圖可以看出，在上述電路參數下，變換器確實工作于DCM模式.圖9給出了參考電流為9.5 A時的時域波形圖和相軌圖，此時變換器工作于混沌狀態，時域波形因失去周期性而顯得雜亂無章，各個開關周期下的幅值跳躍較大，表明混沌狀態是不穩定的，有害的;相軌圖則由一定區域內隨機分布的軌線組成.由仿真結果不難看出，通過PSIM仿真平臺得到的時域波形圖和相軌圖所觀察到的現象與基于離散映射模型繪制的分岔圖所描述的運行狀態完全一致的，證實了離散模型的正確性.

圖6 Ⅰref＝1 A時iL1的時域波形圖和相軌圖

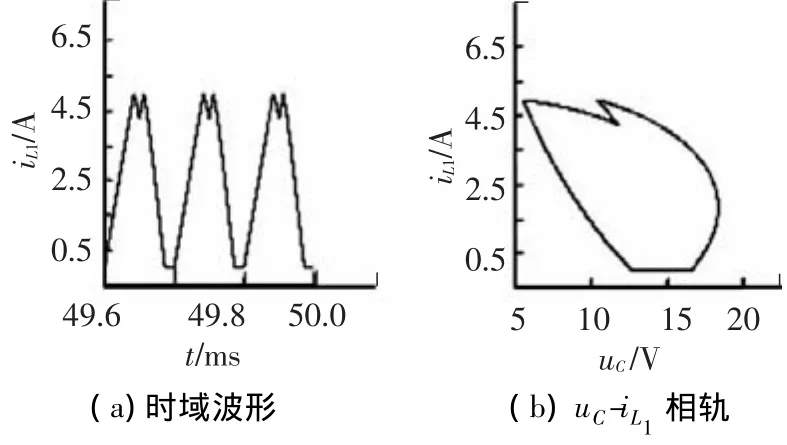
圖7 Ⅰref＝5 A時iL1的時域波形圖和相軌圖

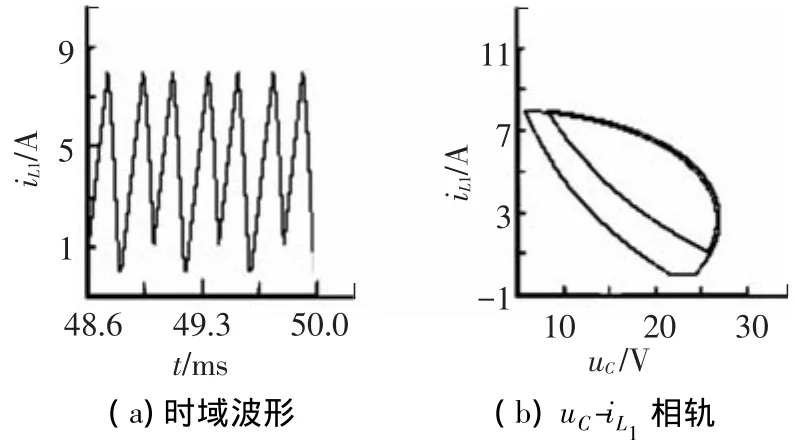
圖8 Ⅰref＝8 A時iL的時域波形圖和相軌圖

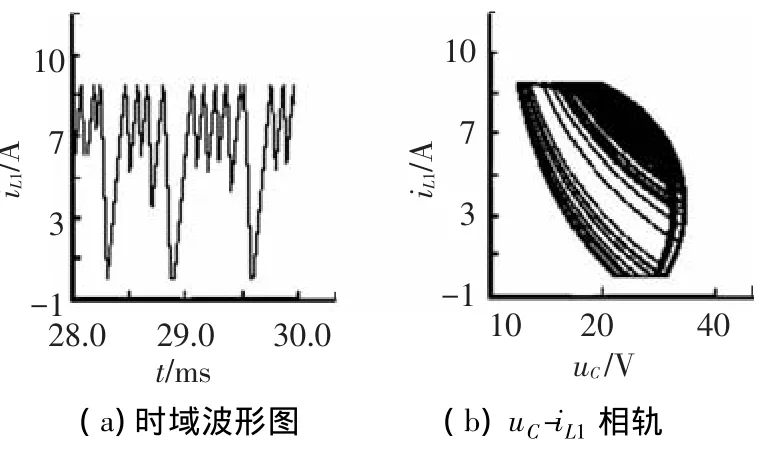
圖9 Ⅰref＝9.5 A時iL1的時域波形圖和相軌圖

5 結 論

1)基于開關電感結構的Buck-Boost變換器雖然在一定程度上提高了傳統Buck-Boost變換器的升/降壓能力，但卻增加了電路的階數，使變換器的運行狀態更容易受到電路參數變化的影響.

2)研究了此新型拓撲結構的變換器在DCM模式下的非線性行為，在分析電路工作原理的基礎上，建立了系統的離散映射模型，并基于此模型繪制了不同參數變化下的分岔圖，發現隨著電路參數的變化，系統經邊界碰撞分岔最終進入DCM陣發混沌狀態.然后通過龐加萊截面更加直觀地反映了不同電路參數下系統的周期態與混沌態，并采用Jacobian矩陣特征乘子的方法確定了首次分岔點的位置和分岔的類型.最后，在PSIM平臺下搭建了符合實際運行條件的仿真模型，通過時域圖和相軌圖觀察變換器在不同參數變化下豐富的動力學演化過程，進一步證明了離散映射模型的正確性.

3)由分岔圖得出當開關電感Buck-Boost變換器工作于DCM模式下時，其工作狀態主要受電流邊界Ⅰb2的影響，電流邊界Ⅰb1對系統穩定性的影響相對較小．

4)基于開關電感結構的Buck-Boost變換器屬于強非線性系統，在設計過程中應選取合適的參數，以確保電路運行在穩定狀態.

［1］AXELROD B，BERKOVICH Y，IOINOVICI A.Switchedcapacitor/switched-inductor structures for getting transformerless hybrid DC-DC PWM converters［J］.IEEE Transactions on Circuits and Systems I，2008，55(2):687-696.

［2］AXELROD B，BERKOVICH Y，IOINOVICI A.Switchedcapacitor(SC)switched-inductor(SL)structures for getting hybrid step-down Cuk/Zeta/Sepic converters［C］//Proceedings of the International Symposium on Circuits and Systems(ISCS).Kos Island，Greece:IEEE，2006:5063-5066.

［3］王詩兵，周宇飛，陳軍寧，等.高階開關功率變換器中的間歇現象［J］.中國電機工程學報，2008，28(12):26-31.

［4］LIU Fang.Intermittency and bifurcation in SEPICs under voltage-mode control［J］.Chinese Physics B，2010，19(8):205-215.

［5］LIU Fang.Fast-scale border collision bifurcation in SEPIC power factor pre-regulators［J］.Chinese Physics B，2008，17(7):2394-2404.

［6］IU H H C，TSE C K.A study of synchronization in chaotic autonomous Cuk DC/DC converter［J］.IEEE Transactions on Circuits and Systems I，2000，47(6):913-918.

［7］劉芳，張浩，馬西奎.電流型單端初級電感變換器中分岔行為與穩定性［J］.電工技術學報，2007，22(9):86-92.

［8］李冠林，李春陽，陳希有，等.電流模式SEPIC變換器倍周期分岔現象研究［J］.物理學報，2012，61(17):170506.

［9］AROUDI A E，LEYVA R.Quasi-periodic route to chaos in PWM voltage-controlled DC-DC boost converter［J］.IEEE Transactions on Circuits and Systems I，2001，48(8):967-978.

［10］CHEN Yanfeng，TSE C K，QIU Shuisheng，et al.Coexisting fast-scale and slow-scale instability in current-mode controlled DC/DC converters:analysis，simulation and experimental results ［J］. IEEE Transactions on Circuits and Systems I，2008，55(10):3335-3348.

［11］BASAK B，PARUI S.Exploration of bifurcation and chaos in buck converter supplied from a rectifier［J］.IEEE Transactions on Power Electronics，2010，25(6):1556-1564.

［12］MAITY S，TRIPATHY D，BHATTACHARYA T K，et al.Bifurcation analysis of PWM-1 voltage-modecontrolled buck converter using the exact discrete model［J］.IEEE Transactions on Circuits and Systems I，2007，54(5):1120-1130.

［13］BAO Bocheng，XU Jianping，LIU Zhong.Mode shift and stability control of a current mode controlled buckboost converter operating in discontinuous conduction mode with ramp compensation ［J］.Chinese Physics B，2009，18(11):4742-4747.

［14］WU Jie， LIU Mingjian， YANG Ping.Study of bifurcation and chaos in the current-mode controlled buck-boostDC-DC converter(I):modelingand simulation［J］.Control Theory and Applications，2002，19(3):387-394.

［15］包伯成，楊平，馬正華，等.電路寬范圍變化時電流控制開關變換器的動力學研究［J］.物理學報，2012，61(22):220502.