氣體擠壓膜邊界影響分析

鄭東桂，馬希直

(南京航空航天大學 機電學院，江蘇 南京 210016)

氣體擠壓膜邊界影響分析

鄭東桂，馬希直

(南京航空航天大學 機電學院，江蘇 南京 210016)

氣體擠壓膜軸承是一種新型的非接觸式氣體支承方式，該支承方式的支承性能主要由間隙內的氣膜壓力分布決定，而氣膜壓力的分布需要通過求解氣體雷諾方程得到。邊界條件對氣體擠壓膜的壓力分布的求解有著顯著影響，因此，確定一個與實際條件接近的邊界條件非常必要。通過流體動力分析方法分析兩種不同邊界區域邊界壓力的變化，給出了新邊界條件下間隙內的壓力和速度分布，結果表明新邊界條件作用時，間隙內氣體與外界環境氣體交換時壓力與速度的變化是連續的。

氣體擠壓膜；邊界條件；壓力；速度

現代工業的發展要求支承方式能夠滿足高速運行的場合，且支承運動的結構精度高，這使得傳統接觸支承方式、氣體靜壓及氣體動壓支承難以滿足要求，因此，研究一種新的滿足要求的非接觸型支承方式顯得非常重要[1]。氣體擠壓膜軸承支承方式是一種非常理想的選擇，它具有工作環境潔凈、摩擦小、磨損低甚至無磨損等優點，具有一定承載能力[2]。

氣體擠壓膜理論分析研究中，根據實際場合不同，采用邊界條件不盡相同。考慮慣性作用時，對擠壓膜的擠壓和擴張兩個過程采用不同的邊界條件，此時邊界效應受擠壓數影響大[3]。對于柔性體，擠壓膜作用時要考慮柔性邊界的作用[4]。研究MEMS裝置擠壓膜效應時，處理邊界效應問題通過增加尺寸，同時考慮邊界條件以匹配數值模擬[5]。考慮氣體擠壓膜的氣體稀薄效應時，對氣體擠壓膜分析要采用滑移速度邊界條件[6-7]。

文中主要探討氣體擠壓膜雷諾方程求解采用的邊界條件的確定，通過對兩種不同邊界條件的分析，選取理想的邊界條件，并分析在該條件下的壓力與速度分布情況。

1 控制方程求解

圖1所示模型在極坐標下，兩平行圓盤氣體擠壓膜支承的控制方程的無量綱形式可表示成[8]：

(1)

圖1 對稱圓盤氣體擠壓膜模型

假定懸浮體固定，則膜厚方程為：

h=ha+e·sin(ωt)

(2)

式中:e為激振板振動振幅。

在數值求解中，通常采用如下邊界條件[9]：

2) 邊緣b1-e1處壓力與大氣壓相等：P(R=1,T)=1；

3) 初始狀態間隙內氣壓為大氣壓：P(R,T=0)=1。

采用上述邊界條件求解得到一個振動周期的壓力分布如圖2，壓力沿半徑方向基本保持不變，邊緣處變化較大。

圖2 氣膜壓力分布圖

2 邊界區域確定及壓力與速度分布

2.1 邊界條件范圍確定

圖1所示的模型中給出了兩種區域邊界條件，模型中上壁面保持靜止。此時A區域的邊界可表示為：u|a-f=u|a-b1=u|e1-f=0，v|a-f=v|a-b1=0，v|e1-f=ωe·sin(ωt)，邊界處b1-e1的壓力被束縛且為大氣壓。B區域的邊界可表示為：u|a-f=u|a-b1=u|e1-f=0，v|a-f=v|a-b1=0，v|e1-f=ωe·sin(ωt)，u|b1-b2=u|b2-c2=u|c2-d2=u|d2-e2=u|e1-e2=0，v|b1-b2=v|b2-c2=v|c2-d2=v|d2-e2=v|e1-e2=0，p|b1-b2=p|b2-c2=p|c2-d2=p|d2-e2=p|e1-e2=pa，pa為大氣壓。與A區域邊界相比，B區域邊界的氣流的速度和壓力均可以得到充分發展，即遠場邊界條件使得擠壓膜間隙內的氣流可充分發展。

現采用ANSYS軟件進行分析。模型中氣膜厚度很小，只有幾十微米，而圓盤半徑遠大于膜厚尺寸，為25mm；區域B采用遠場邊界條件確定尺寸。由分析發現，在邊界處兩種區域邊界的氣體壓力都發展的比較充分，非常接近大氣壓，但是區域A氣流的速度沒有得到充分發展，而區域B得到充分發展，基于這點，采用區域B做邊界條件是更合適的，如圖3和圖4所示。

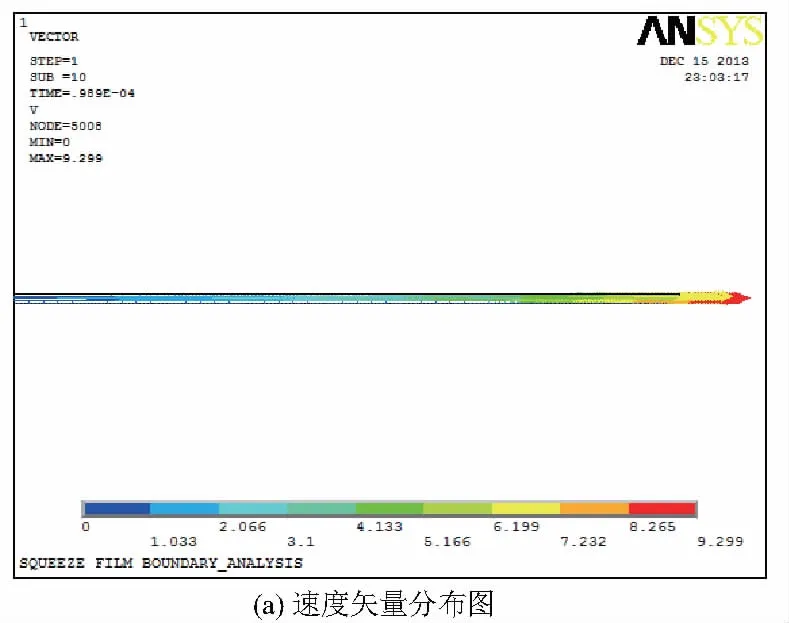
圖3 e=1μm，σ=418.28區域A速度與壓力分布

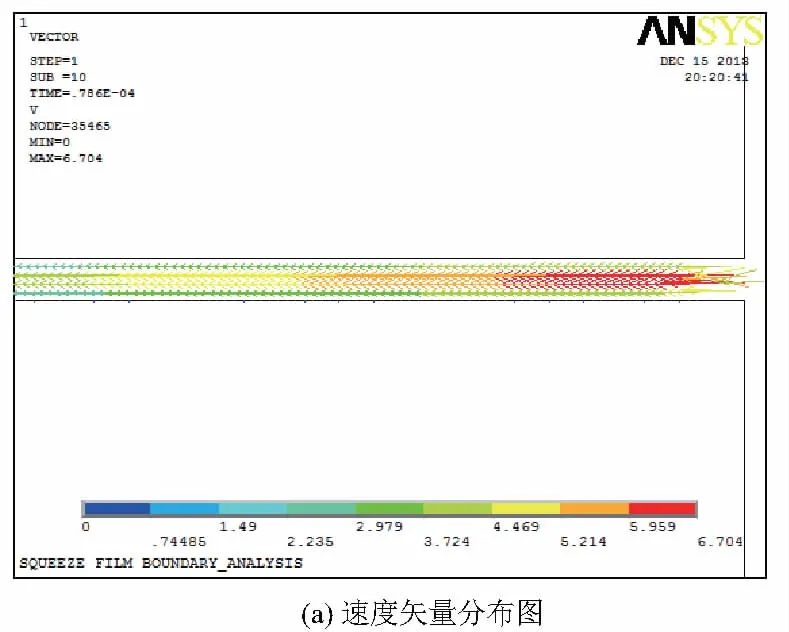
圖4 e=1μm，σ=418.28區域B速度與壓力分布

2.2 區域B邊界壓力與速度分布

經上述分析可確定區域B所示邊界條件更為接近實際情況，在該邊界條件作用下，間隙內的氣體沿膜厚方向的速度分布呈拋物線形分布，且大部分的氣體處于中低速狀態，即遠小于邊界b1-e1上的速度值，如圖4(a)。間隙內大部分區域，除邊緣附近小部分區域外，氣體的壓力與中心壓力基本相同，如圖5。這說明擠壓膜在高頻振動時，間隙內大部分氣體的流動不能立刻得到響應，有一個延遲階段。區域A間隙內的氣體與外部環境氣體交換時，在邊界b1-e1上氣體壓力和速度變化是突變過程，不連續；區域B的氣體從間隙流入外部環境時壓力和速度是連續變化的。

圖5 間隙氣體壓力分布情況壓力

3 結語

1) 與傳統邊界條件相比，遠場邊界條件更接近實際情況。

2) 傳統邊界條件作用下，間隙內的氣體與外界環境大氣交換時，氣體壓力和速度在邊界b1-e1上突變為環境氣體的壓力和速度，使得壓力和速度變化不連續，與實際情況有較大差異；采用遠場邊界條件時，間隙內氣體的速度和壓力的變化是連續性的，且逐漸變化為環境氣體壓力和速度。

[1] Stolarski T.A., Chai Wei. Load-carrying capacity generation in squeeze film action. Int J Mech Sci, 2006,48(3):736-741.

[2] 王勝光, 馬希直. 氣體擠壓膜承載能力的實驗研究[J]. 機械制造與自動化，2013, 41(1)：20-21,47.

[3] Jin Li, Wenwu Cao al. et. Influence of gas inertia and edge effect on squeeze film in near field acoustic levitation. Applied Physics Letters, 2010,96:243507-1-243507-3.

[4] Jin Li, Jing Wu and Jiaqi Ren. High order numerical study of gas squeeze film with flexural boundary. Applied Mechanics and Materials, 2012,(152/154):462-467.

[5] Satish Vemuri, Gary K. Fedder and Tamal Mukherjee. Low-order squeeze film model for simulation of MEMS devices. In Proceedings of the 2000 Int. Conf. on Modeling and Simulation of Microsystems Semiconductors, Sensors and Actuators, San Diego, CA, 2000:205-208.

[6] Lin Wu. A slip model for rarefied gas flows at arbitrary Knudsen number. Applied Physics Letters, 2008,93:253103-1-253103-3.

[7] Daniel D.Joseph. Boundary conditions for thin lubrication layers. Phys. Fluids, 1980,23(12):2356-2358.

[8] E.O.J.Salbu. Compressible squeeze films and squeeze bearings. ASME Journal of Basic Engineering, 1964:355-364.

[9] A. Minikes, I. Bucher. Coupled dynamics of a squeeze-film levitated mass and a vibrating piezoelectric disc: numerical analysis and experimental study. Journal of Sound and Vibration, 2003,263:241-268.

Analysis of Boundary Effect of Gas Squeeze Film

ZHENG Donggui, MA Xizhi

(School of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Gas squeeze film bearing is a new non-contact gas bearing, its supporting performance deperds on the film pressure in the gas squeeze film gap. The distribution of pressure is obtained by solving the Reynolds equation with squeeze term. Because the boundary condition has influence on its pressure distribution greatly, it is important to defermine it. This paper analyzes the variation of two different boundaries by fluid dynamic analysis method and obtains the distribution of the pressure and velocity in the gap of the new boundary. The result shows that, the pressure and velocity vary continuously in exchange of the gap and external gas in the new boundary.

gas squeeze film; boundary condition; pressure; velocity

鄭東桂(1987-)，男，江西贛州人，碩士研究生，主要研究方向為流體潤滑理論。

TH123+.4

B

1671-5276(2015)05-0029-02

2015-03-02