Weibull 壽命型產品可靠性序貫驗證試驗方法

王 琳，吳海橋，宗茜茜

(南京航空航天大學民航學院，南京 211106)

可靠性試驗是為了解、評價、分析提高產品可靠性而進行的試驗的總稱，通常包括環境應力試驗、可靠性增長試驗、可靠性鑒定試驗和驗證試驗［1］。可靠性驗證試驗用于驗證產品的可靠性是否達到規定標準，通過度量并給出試驗驗證值，可為研制階段的產品提供設計改進措施，以及對產品的驗收過程提供合理的判決依據。其中，通常定時截尾試驗由于便于控制試驗的進程而得到采用，但試驗需要的樣本量較大，而定數截尾方式適用于小樣本下的可靠性驗證［2］。而序貫抽樣試驗方法能利用試驗中產生的過程信息不斷做出判斷，而無需等到將試驗進行到規定的截止時間或失效數為止時再進行判斷，在最大程度上利用了試驗的有效數據。因此，一般情況下，與定時或定數截尾等一次抽樣試驗方法相比，序貫抽樣試驗方法做出判斷所用的平均累積試驗時間較短、平均失效數較小，可縮短試驗時間和節省試驗費用。周桃庚等［3］討論了Weibull 分布下的貝葉斯可靠性序貫驗證試驗方法，并以某光電儀器為例，制定了以平均壽命為指標的序貫驗證試驗方案，該方法可節省試驗時間、降低試驗成本，提高試驗數據利用率及試驗效率，但要求了解參數的先驗信息，再利用這些信息來估計出先驗分布中的參數，進而制定貝葉斯可靠性序貫驗證試驗方案。鄧清等［4］討論當產品的壽命為對數正態分布時，在給定對數標準差的前提下的截尾序貫驗證試驗方案。

此外，目前國內外文獻所提出的序貫抽樣試驗方法均基于產品壽命服從指數分布假設［5-6］，具有一定的局限性，給出的試驗標準對大多數機電產品并不適用。基于此，陳文華［7］等通過將Weibull 分布轉化為指數分布的形式，根據指數分布序貫驗證試驗理論，推導出了適用Weibull 分布產品的可靠性序貫抽樣驗證試驗方法，但該方法在樣本數較少的試驗中不能做出有效判決。Tzong-Ru Tsai［8］基于形狀參數已知、尺度參數為隨機變量的基礎假設，建立了在試驗設備有限的條件下Weibull 壽命型產品的抽樣試驗方案，并通過計算驗證了其合理性。Daryl J. Hauck［9］等依據標準中的序貫驗證方案只適用于指數分布而不適用于Weibull 分布，指出了Weibull 壽命型序貫驗證試驗中將Weibull 分布轉化為指數分布時其形狀參數并不是已知的，而是未知的，需要進行準確估計。樓洪梁［10］等在Daryl J.Hauck 等的基礎上，以滾動軸承的序貫抽樣試驗為研究背景，根據Weibull 壽命型產品的序貫驗證試驗理論，研究了Weibull 分布形狀參數的變化對產品接收和拒收概率的影響，并通過模擬試驗定量分析了形狀參數變化時產品接收和拒收概率的變化情況。

本文在現有研究基礎上，針對多數非電子產品的故障前平均工作時間(MTBF)服從或近似服從Weibull 分布，而不服從指數分布的實際情況［11］，研究分析了Weibull 壽命型產品的序貫驗證試驗方案，并實例說明了選擇合理的試驗方案能夠一定程度提高可靠性驗證試驗的效率及其有效性。

1 Weibull 分布下可靠性序貫驗證試驗

1.1 轉化為指數分布形式的Weibull 分布序貫概率比試驗方案

雙參數Weibull 分布的概率密度函數f(t)和分布函數F(t)分別為

其中:m 為形狀參數;η 為尺度參數。

設隨機變量X 服從雙參數Weibull 分布，記概率密度函數為f(x，θ)(θ 為壽命參數)。假設其MTBF 檢驗上限為θ0，檢驗下限為θ1，則樣本總體為f(x，θ)的樣本(x1，x2，…，xn)，其隨機變量X1，X2，…，Xn的聯合概率密度函數為:

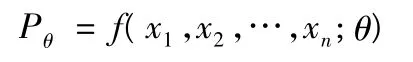
若θ=θ0，則Pθ0=f(x1，x2，…，xn;θ0)=1 -α;

若θ=θ1，則Pθ1=f(x1，x2，…，xn;θ1)=β。

其中:α 為生產方風險;β 為使用方風險。

定義概率比為Pθ0/Pθ1。按序貫抽樣試驗規則，預先選取兩個常數A 和B 作為判斷界限。Wald 提出的序貫試驗判斷界限為［8］:令

若Pθ0/Pθ1≤B，則θ =θ0，接收(Pθ0大，高概率接收); 若Pθ0/Pθ1≥A，則θ=θ1，拒收(Pθ1大，高概率拒收);若B ＜Pθ0/Pθ1＜A，則無法做出判斷，需繼續試驗。

GJB 899A—2009(《可靠性鑒定和驗收試驗》)中，將雙參數Weibull 分布轉化為單參數的指數分布［7］，推導出Weibull 分布的序貫試驗方案，給出了指數分布序貫驗證試驗的判斷準則。由

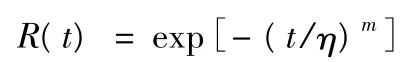
可得θ=ηm= -［t(R)］m/InR(R 為給定的可靠度)。

式(2)可寫成如下積分的形式

令y=xm，θ=ηm，則

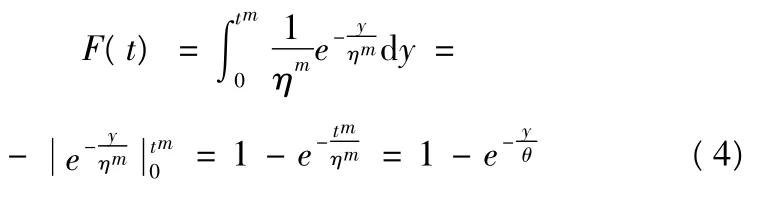
此時，y 服從指數分布。按此方法，Weibull 分布轉化成了指數分布。若N 個樣品進行非替換序貫試驗，在t 時刻前有r 個樣品失效，記t(i)為第i 個樣品失效時間，則t(1)，t(2)，…，t(r)的聯合概率密度為

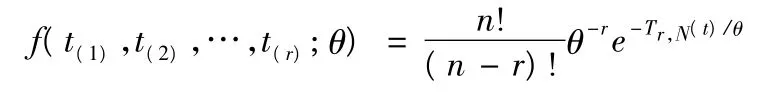
Weibull 壽命型非替換序貫驗證方案如下:

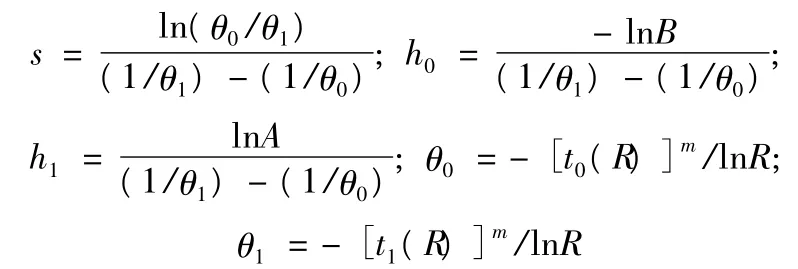
1.2 非電子產品序貫概率比驗證試驗方案

［13］給出了通常情況下非電子產品的序貫概率比驗證試驗方案:

接收方程為

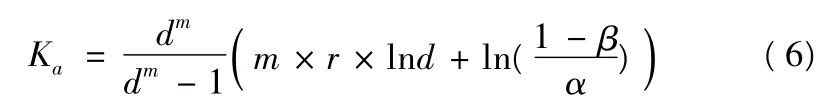
拒收方程為

將產品逐個投入試驗，每出現一個故障，即與接收、拒收判據比較，或在試驗中跟蹤描點，直至做出接收或拒收判決。

1.3 非電子產品序貫概率比驗證試驗方案的快速判決

參考文獻［13］給出了在小樣本情況下，非電子產品序貫概率比驗證試驗方案的快速判決方法。若式(8)成立，則接收，認為θ=θ0;

若式(9)成立，則接收，認為θ=θ1。

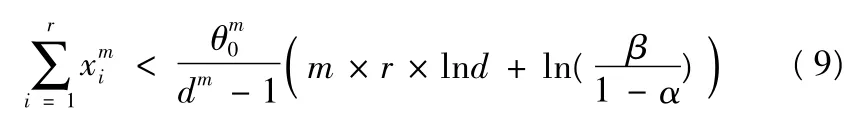
2 不同序貫驗證試驗方案的判決情況對比

某型機械設備故障服從Weibull 分布，且m =2［11］，α =β=0.20，θ0=270 h，θ1=135 h。選取3 臺設備進行試驗，數據如表1 所示。可獲得產品樣本數較少，用以下不同的試驗方案做出判決。

表1 某型機械設備故障時間

1)采用1.1 的試驗方案，但合同中沒有給出R 的取值，因此推導出的Weibull 分布可靠性序貫驗證試驗方案具有局限性。若令R=0.9，則t0(R)=270 h，t1(R)=135 h，轉化后的θ1= -［t1(R)］m/lnR =1.729 8 ×105，θ0= -［t0(R)］m/lnR=6.919 1 ×105=4θ1。由α = β =0.20，m =2，d =2 查GJB 899A—2009，根據圖A.23 試驗統計方案，得出對應的定數截尾驗證試驗方案的截尾故障數為6。取該截尾數的3 倍作為同等要求下的定數截尾序貫驗證試驗的截尾數［14］，則該實例中截尾數r=18。但由于試驗經費和時間限制，該實例只投入了3 個試驗樣品，遠達不到所需的18 個試驗樣品的要求，因而不能做出判決。

2)采用1.2 的試驗方案，由式(6)和式(7)計算故障數r與K 之間的關系如下:

(1，K)=(1，1.075 4)，(2，K)=(2，3.978 1)，(3，K)=(3，10.699 6)。在Matlab 中繪制函數圖像并描點，如圖1 所示，在K=10.699 6 處得到接收判決。

3)采用1.3 的試驗方案，將前兩個故障時間分別代入式(8)、(9)，既不能得到接受判決也不能得到拒收判決，故繼續試驗，試驗進行到第3 個設備故障時，有:

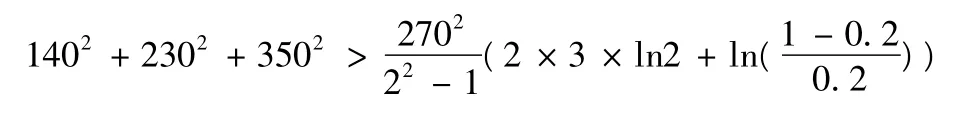
即:195 000 ＞134 747.81，因此可以做出接收判決，總試驗時間為720 h。

4)采用GJB 899A—2009 中的標準試驗方案，直接用指數分布下的序貫驗證方法，計算得試驗時間t 與故障數r 之間繼續試驗方程為

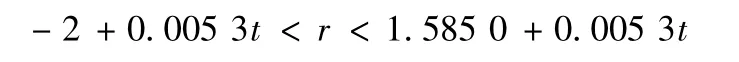
分別以故障數r(縱坐標)與總試驗時間t(橫坐標，θ1的倍數)描點，在Matlab 中繪制的圖形如圖2 所示。不同方案下的判決情況如表2 所示。

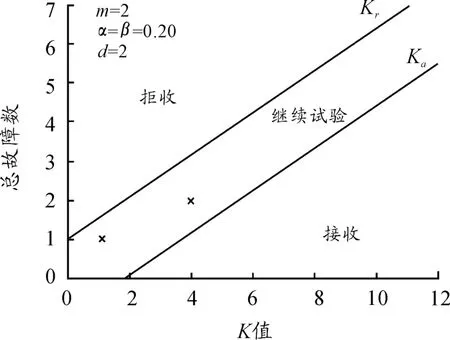
圖1 采用1.2 方案序貫試驗結果示意圖

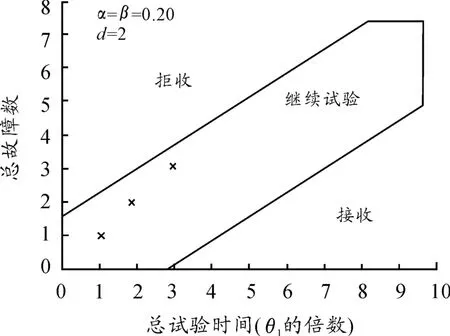
圖2 采用GJB 899A—2009 序貫試驗方案結果示意圖

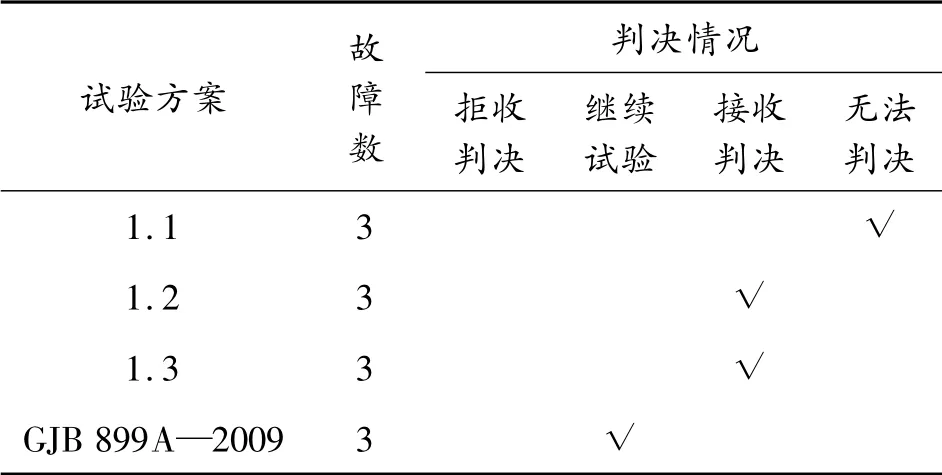
表2 不同序貫驗證試驗方案的判決情況對比

從上述試驗方案的設計和分析結果可以看出，不同驗證試驗方案的選取對結果的影響較大:采用1.1 的試驗方案，需要樣本數較多，但由于樣本數和總試驗時間的限制，不能做出有效判決;采用1.2 的試驗方案，可以直觀地通過圖像看出故障數與試驗時間相對應的點落入的范圍，從而做出正確判決;對于小樣本試驗，采用1.3 的試驗方案可以快速做出判決，但對于較大的樣本計算量也將偏大; 基于故障服從指數分布的假設，直接采用GJB 899A—2009 中的試驗方案，做出的判決為繼續試驗，而該設備故障實際服從威布爾分布，該基本假設不正確，從而導致判決結果不準確。

3 結束語

針對多數非電子產品的故障前平均工作時間(MTBF)服從或近似服從Weibull 分布，而不服從指數分布的實際情況，以及國內外文獻給出的試驗標準對大多數非電子產品并不適用這一問題，本文根據非電子產品的序貫抽樣試驗和指數分布的序貫試驗理論，研究分析了Weibull 壽命型產品的可靠性序貫驗證試驗方案，著重比較論述不同方案下的試驗結果及其差異，并實例說明了選擇合理的試驗方案能夠一定程度提高可靠性驗證試驗的效率及其有效性。在進行壽命服從或近似服從Weibull 分布的產品可靠性序貫驗證試驗時，應根據實際樣本容量及其他實際因素來確定試驗方案的參數，有根據地選取試驗方案，從而更有效地根據試驗結果做出相應的正確判決。如何根據序貫試驗理論制定更為簡便有效的Weibull 壽命型產品的驗證試驗方案將是下一階段的研究重點。

參考文獻:

［1］GJB 450A—2004，裝備可靠性工作通用要求［S］.

［2］陳文華，柴新，盛軍鑫，等.Weibull 壽命型產品可靠性定數截尾驗證試驗方法［J］.浙江大學學報，2001，35(2):128-130.

［3］周桃庚，沙定國.貝葉斯可靠性序貫驗證試驗方法［J］.儀器儀表學報，2011，22(4):373-374.

［4］鄧清，袁宏杰.對數正態分布壽命型序貫驗證試驗方法［J］.北京航空航天大學學報，2012，38(12):1653-1656.

［5］MIL—STD—781D.Military Standard Reliability Testing for Engineering Development，Qualification，and Production［S］.

［6］陳文華，柴新，石永剛.Weibull 壽命型產品可靠性序貫驗證試驗方法［J］. 儀器儀表學報，1999，20(5):493-496.

［7］Tzong-Ru Tsai，Yu-Ting Lu，Shuo-Jye Wu.Reliability sampling plans for Weibull distribution with limited capacity of test facility［J］.Computers ＆ Industrial Engineering，2008(55):721-728.

［8］Daryl J，Hauck J，Bert Keats.Robustness of the exponential sequential probability ratio test (SPRT)when Weibull distributed failures are transformed using a“known”shape parameter［J］. Microelectronics Reliability，1997，37(12):1835-1840.

［9］樓洪梁，李興林.Weibull 分布形狀參數對軸承序貫驗證試驗的影響［J］.軸承，2011(4):34-36.

［10］李鑫，蔡景，周月.Weibull 分布可靠性序貫驗證試驗方案選擇及分析［J］.工程與試驗，2013，53(2):4-7.

［11］姜同敏，王曉紅.可靠性試驗技術［M］.北京:北京航空航天大學出版社，2012.

［12］曾天翔.可靠性及維修性工程手冊(下冊)［M］.北京:國防工業出版社，1995.

［13］李根成，姜同敏.定時截尾可靠性鑒定試驗方案的參數選擇及分析［J］.航空學報，2006，27(2):272-274.