數形結合方法在高中數學教學中的應用

徐兵

【摘 要】我國的教育正處在深化改革階段，而高中數學在學生的學習生活中比較重要，所以加強高中數學的教學有效性就顯得格外重要。數形結合方法是一種比較應用廣泛的教學方法，能對高中數學教學起到促進作用。本文主要就高中數學教學中數形結合方法的實際應用進行詳細探究，希望此次的理論研究對實際教學有所裨益。

【關鍵詞】數形結合 ? 高中數學 ? ? 應用

一、引言

數學是研究空間形式及數量關系的一門科學，學習數學的主要目的之一是解決實際生活中的問題，數學思想方法在整個高中的數學課程中都有體現，是數學教學不可缺少的內容。在諸多的數學教學方法中，最為重要的就是數形結合這一教學方法，其能夠從不同的角度將實際的數學知識呈現出來，并能夠靈活地解決實際問題。

二、數形結合思想類型及主要作用分析

1.數形結合思想方法分析

數形結合思想類型多樣，其中有由形思數及一方面是借助形的生動性及直觀性闡釋與數之間的關系，最為顯著的就是對函數圖象的應用來說明函數性質;另一方面則是在數的精確性及嚴密性特點下對形的直觀性進行闡釋，最為顯著的就是通過曲線方程對曲線幾何的性質進行精確闡釋。這一方法的應用往往能夠將比較復雜的問題直觀化，拓展解題思路。數形結合思想方法可分為由數思形、由形思數、數形互化三類。

2.數形結合方法的主要作用分析

數形結合方法對高中數學教學有著重要作用，它能夠促使學生形成和諧完整的數學概念。數學概念是數學邏輯起點，這也就構成了學生的認知基礎，采取數形結合的思想方法能夠將兩種形式表述概念中的數形得到有機結合，進而揭示實質性的內容。不僅如此，還能夠促進學生數學思維能力的發展。高中數學教學注重數形結合思想，促使學生抓住數學問題的實質，加強對其的認識，對其創造性的思維形成有著重要的促進作用，有助于學生掌握、理解所學的知識。

三、高中數學教學中數形結合方法

1.高中數學教學中數學結合方法應用原則

高中數學教學中數形結合法的應用要遵循相應的原則，如此才能充分發揮其作用。需要遵循的原則主要有雙向性原則、等價性原則、直觀性原則、簡潔性原則、實踐創新原則。雙向性原則主要是對代數進行抽象探究的同時也對幾何圖形加以直觀性分析。等價性原則主要就是數與形性質轉換應當是等價的，也就是針對問題的圖象表示有數反映的數量關系要一致。簡潔性原則是數形轉換要盡可能地使得構圖簡單合理，避免復雜煩瑣的運算，從而實現化難為易的目的。還有就是實踐創新原則，這個原則比較重要，由于數學思想方法要比具體的知識抽象，所以要能夠結合實際進行應用，要提出符合學生數學認知水平及規律的問題，提升學生的空間想象能力。

2.高中數學教學中數形結合方法的實際應用

數形結合方法在高中數學教學中應用很廣泛。其中在同角三角函數關系教學當中的應用就體現得比較充分，同角三角函數關系的推導中，采取數形兩個角度進行推導平方關系及商數關系。

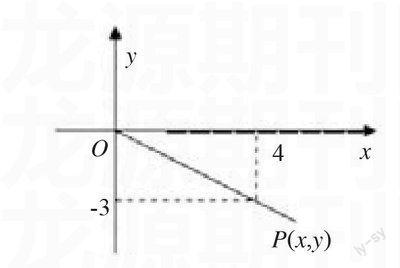
例如：已知tanα=-3/4，并且α是第四象限角，求sinα和cosα。根據這一題目的要求，可以用兩種方法對其進行解決，首先就是運用圖形解決問題：

結合相關的定義以及上圖可知，在角α終邊上的點就是（4，-3），|OP|=5，這樣就能夠得知cosα=4/5，而sinα=-3/5。本題的解題思路主要就是通過題目中的已知條件畫出相應的圖象，這樣就能夠直觀性地對題目的要求有了了解，不用通過復雜的方程進行求解，比較簡單。如果是通過三角函數的基本關系進行求解就會比較復雜，sinα/cosα=-3/4，sin2α+ cos2α=1。這樣就能夠求得sinα=-3/5，cosα=4/5。相比之下還是圖形解法較為簡單直觀。

另外，還可以將數形結合的方法應用于圓錐曲線及直線的教學當中。解析幾何研究幾何的主要方法是坐標法，在直線和圓錐曲線當中，以數和圖形為工具，用數形結合的代數方法也能夠解決實際問題。在直線和圓的教學，應用數形結合也能夠起到很好的作用，從不同角度刻畫直線傾斜角度，能夠在實際的教學中直觀地體現出來，從而讓學生更方便了解。

四、結語

總而言之，高中的數學教學比較重要，采取有效的教學方法能夠減輕學生的學習壓力，使得學生更快速地掌握數學知識，開拓了解題思維。數形結合的方法有效地解決了實際教學中的難題，對學生的學習成績提升有著重要促進作用，同時也能提升高中的數學教學質量。

【參考文獻】

[1]楊渭清.談中學數學思想方法的教學[J].青海教育，2014（04）.

[2]張子民.如何把數學思想方法滲透于教學始終[J].遼寧師專學報（自然科學版），2013（01）.

[3]王向秀.滲透數學思想 強化思維訓練[J].紹興文理學院學報，2014（01）.