約束自適應桁架優(yōu)化設計方法

肖阿陽， 王本利， 金耀初

1. 哈爾濱工業(yè)大學 衛(wèi)星技術研究所，哈爾濱 150001； 2. 薩里大學 計算科學系，吉爾福德 GU2 7XH)

?

約束自適應桁架優(yōu)化設計方法

肖阿陽1， 王本利1， 金耀初2

1. 哈爾濱工業(yè)大學 衛(wèi)星技術研究所，哈爾濱 150001； 2. 薩里大學 計算科學系，吉爾福德 GU2 7XH)

為求解多峰值、高度非線性桁架尺寸及形狀優(yōu)化問題，減少算法參數設置的盲目性，將Oracle罰函數與啟發(fā)式算法相結合，提出可自適應處理約束列式的優(yōu)化算法Ω-CMA-ES。該算法在處理各類復雜桁架優(yōu)化問題時僅需設置一個參數Ω。測試算例表明，該算法對參數Ω具有良好的魯棒性，可有效處理各類動態(tài)約束；且在探索全局最優(yōu)解時體現出較高潛力，優(yōu)化質量及收斂速度優(yōu)于既有結果。

桁架優(yōu)化；Oracle罰函數；啟發(fā)式算法；約束優(yōu)化問題；Ω-CMA-ES

結構優(yōu)化設計因經濟效益顯著一直是工程領域熱點問題。桁架尺寸優(yōu)化設計是最先被研究的結構優(yōu)化課題之一。在桁架尺寸優(yōu)化設計中，桿件截面積及截面形狀參數均可作為設計變量，而桿件長度、桁架包絡、節(jié)點數及節(jié)點連接方式均已固定。桁架形狀優(yōu)化設計則致力于對桁架節(jié)點坐標的優(yōu)化，而桁架本身拓撲不變。常認為優(yōu)化桁架形狀較桁架尺寸更具效率[1]。

因工程需要，桁架尺寸、形狀同步優(yōu)化設計[2-4]常被設定含約束的混合整數非線性規(guī)劃問題(MINLPc)。同時引入尺寸、形狀變量會增加桁架優(yōu)化問題難度，計算量增大。受制于計算機硬件性能及優(yōu)化算法性能，相關研究主要采用分層優(yōu)化法；但因桁架尺寸、形狀變量在優(yōu)化進程中具有強耦合性，分層優(yōu)化法易丟失有價值的可行解，且會陷入局部最優(yōu)，故諸多研究致力于應用啟發(fā)式算法，通過單層優(yōu)化實現桁架尺寸及形狀優(yōu)化設計。

對桁架約束優(yōu)化問題而言，約束列式處理非常重要。目前廣泛采用的包括靜態(tài)罰函數法、動態(tài)罰函數法及自適應罰函數法等。而所有罰函數法均應正確權衡目標函數及約束違反程度[5-6]。罰函數過大或過小時設計向量間僅基于罰函數或目標函數，會影響算法的尋優(yōu)廣度或深度。桁架優(yōu)化問題中混合變量、復雜力學約束的存在使罰函數設置尤其關鍵。在桁架優(yōu)化中采用靜態(tài)罰函數會致全局最優(yōu)解丟失概率增大，甚至得不到可行解。

本文試圖從約束自適應處理及優(yōu)化算法性能提升角度，構造高效率、自適應桁架優(yōu)化設計方法。通過3個典型優(yōu)化算例顯示，所提Ω-CMA-ES算法對復雜約束的桁架尺寸、形狀優(yōu)化問題適應性較廣。

1 桁架尺寸及形狀優(yōu)化模型

結構優(yōu)化宗旨即實現滿足約束條件的結構輕量化設計。就桁架尺寸、形狀優(yōu)化而言，其設計變量主要包括桿件截面積(尺寸變量)及節(jié)點坐標(形狀變量)。結構重量極小化桁架尺寸及形狀優(yōu)化問題可描述為

(1)

(2)

(3)

XA={A1A2…Ai…Ane}T∈ΔA

(4)

XG={G1G2…Gj…Gnj}T∈ΔG

(5)

X={XA,XG}T

(6)

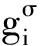
2 Ω-CMA-ES算法

含應力或多階頻率約束，同時考慮尺寸、形狀變量桁架優(yōu)化設計為高度非線性非凸優(yōu)化問題[7-8]。全局優(yōu)化算法如啟發(fā)式算法應用為解決此類問題的關鍵。自適應協(xié)方差矩陣進化策略(CMA-ES)作為新型啟發(fā)式算法，其出色的全局尋優(yōu)性能已獲廣泛認可。而標準CMA-ES為無約束優(yōu)化問題而設計，因此本文運用Oracle罰函數法[9]將含動態(tài)約束桁架尺寸、形狀優(yōu)化問題轉化為無約束優(yōu)化問題。

2.1 Oracle罰函數

罰函數法核心即將約束優(yōu)化問題改造為無約束優(yōu)化問題。改造后的目標函數F(X,C)由初始目標函數f(X)、懲罰因子C及約束函數V(X)組成，即

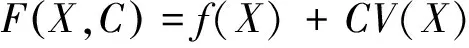
(7)

有研究認為，合理確定懲罰因子C的數值尺度為罰函數法難點。一般而言，在靜態(tài)罰函數中C為固定值；在動態(tài)罰函數中C為關于優(yōu)化迭代次數的函數；在自適應罰函數中C則為特殊設計的自適應懲罰因子，可自適應地調整自身數值尺度。為確保搜索廣度，啟發(fā)式算法的初始種群隨機生成。因此，在優(yōu)化過程起始階段，種群中可行解比重較小，此時賦予非可行解較大懲罰因子C利于引導算法快速搜索到可行解。隨可行解在種群中的比重逐步提升，懲罰因子C應隨之減小，從而利于算法對問題可行域進行深度搜索。

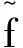
(8)

Subjectto:g0(X)=f(X)-Ω=0

(9)

gj(X)=0, (j=1,2,…,me)

(10)

gj(X)≥0,(j=me+1,…,m)

(11)

式中：Ω為Oracle參數；me為等式約束個數；m為所有約束個數。

優(yōu)化進程中，Ω采用更新機制以追蹤目標函數值的變化情況，即

(12)

式中：i為第i次優(yōu)化迭代；res為剩余函數，代表設計向量約束違反程度。當且僅當res(X)=0時X為可行解。

Oracle罰函數的剩余函數res(X)、罰函數方程p(X)及自適應系數α分別為

(13)

(14)

(15)

式(14)為改造后的無約束優(yōu)化問題目標函數。在初始目標函數f(X)及剩余函數res(X)數值尺度差異未知情況下，Oracle罰函數法只需保證Ω的初始值為一較大值。隨機優(yōu)化初始階段，若Ω初始值足夠大，附加約束g0(X)≤0，由式(15)可知，自適應系數α=0。此時，式(14)中目標函數p(X)的取值等同于剩余函數res(X)，即設計向量之間的比較僅基于約束違反程度。優(yōu)化算法首次搜索到的可行解必為最優(yōu)解。此后優(yōu)化進程中，式(12)可保證g0(X)始終為一小量。基于式(9)對初始目標函數轉化，式(14)、(15)可實現在同一數值尺度上動態(tài)權衡設計向量的初始目標函數值f(X)及約束違反程度res(X)。

2.2 自適應協(xié)方差矩陣進化策略

CMA-ES為在進化策略(ES)基礎上產生的高效率全局優(yōu)化算法[10]。其以符合正態(tài)分布N(X,σ)的個體突變?yōu)橹饕阕印Ｆ渲胁介Lσ為個體x的突變強度。在此基礎上ES引入旋轉角α以調整x突變方向。ES中旋轉角設定常取固定值并施以隨機擾動，但其中所含無效突變會提高整體計算成本。

λ=4+floor(3log(N))

(16)

CMA-ES[11]基于歷史搜索路徑信息及相鄰兩代中μ個最佳個體(μ=floor(λ/2))間向量差更新協(xié)方差矩陣C，從而調整群體的突變方向。CMA-ES算法所有參數均無需用戶調節(jié)，其自適應機制可改進算法收斂速度、提高算法的全局搜索能力。該算法已被證明在全局優(yōu)化方面均具有高可靠性及競爭力。

2.3 Ω-CMA-ES算法框架

由于桁架尺寸、形狀優(yōu)化問題中不含等式約束，且相關不等式約束形式均為gj(x)≤0。剩余函數res(X)可由式(13)轉化為

res(x)=

(17)

綜合Oracle罰函數及CMA-ES算法的內在機制，適用于桁架尺寸、形狀優(yōu)化問題的Ω-CMA-ES的算法框架設計如下：

步驟1：設置優(yōu)化問題終止條件，初始化Oracle罰函數參數Ω；

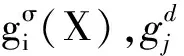
步驟3：找出當前種群中剩余函數值res(X)=0的子種群，選取最優(yōu)個體，記錄目標函數值f(X)為fi。設迭代次數i=i+1；

步驟4：據式(12)更新罰函數參數Ω；

步驟5：利用CMA-ES算法機制產生新種群；

步驟6：重復執(zhí)行步驟3～5，直到滿足迭代終止條件，輸出最優(yōu)設計向量及目標函數值。

3 優(yōu)化算例

用含平面、空間桁架的3個經典算例測試Ω-CMA-ES的普適性及優(yōu)化效率。所用結構力學分析方法為有限元法。Ω-CMA-ES種群規(guī)模由式(16)確定。在測試算例中，參數Ω均采用106，109兩種初始值。

3.1 15桿平面桁架(算例1)

15桿平面桁架初始結構見圖1。桿單元許用應力區(qū)間為[-172.369,172.369]MPa，垂直方向載荷作用于節(jié)點8，含23個設計變量，即尺寸變量Ai,(i=1,2,…,15)；形狀變量x2=x6;x3=x7，y2，y3，y4，y6，y7，y8。材料參數、相關設計約束見文獻[2]。

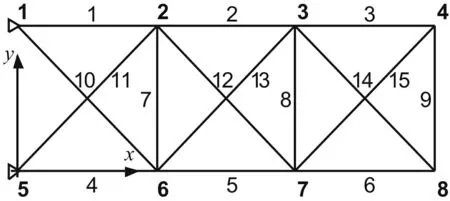
圖1 十五桿平面桁架初始結構Fig.1 Schematic of the planar 15-bar truss

有限元分析最大次數設為4 000。在兩種Ω參數初始值設置情況下，所得最優(yōu)設計見圖2。Ω參數自適應變化曲線見圖3。由圖3看出，因第一代種群中已有可行解，Ω1取值迅速回到1 000以內。本文方法與其它最優(yōu)解比較見表1。由表1看出，Ω-CMA-ES算法在約束控制上有不俗表現，優(yōu)化所得結構質量最優(yōu)，且結構重分析次數最小。

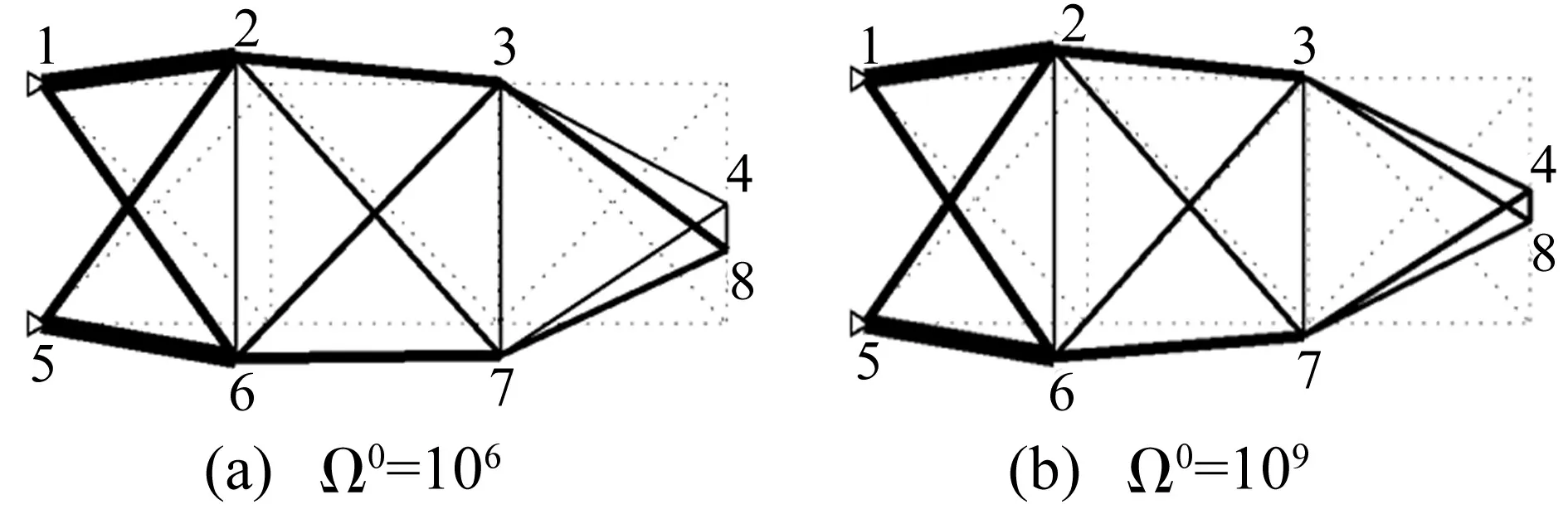
圖2 兩參數初始值設置下15桿平面桁架最優(yōu)布局設計Fig.2 Best solutions of the planar 15-bar truss layout under two different cases of parameter initial value

圖3 Ω參數變化曲線Fig.3 Variation curves of parameter Ω

表1 十五桿平面桁架的布局優(yōu)化結果對比

Tab.1 Comparison of optimized designs found for the planar 15-bar cantilever

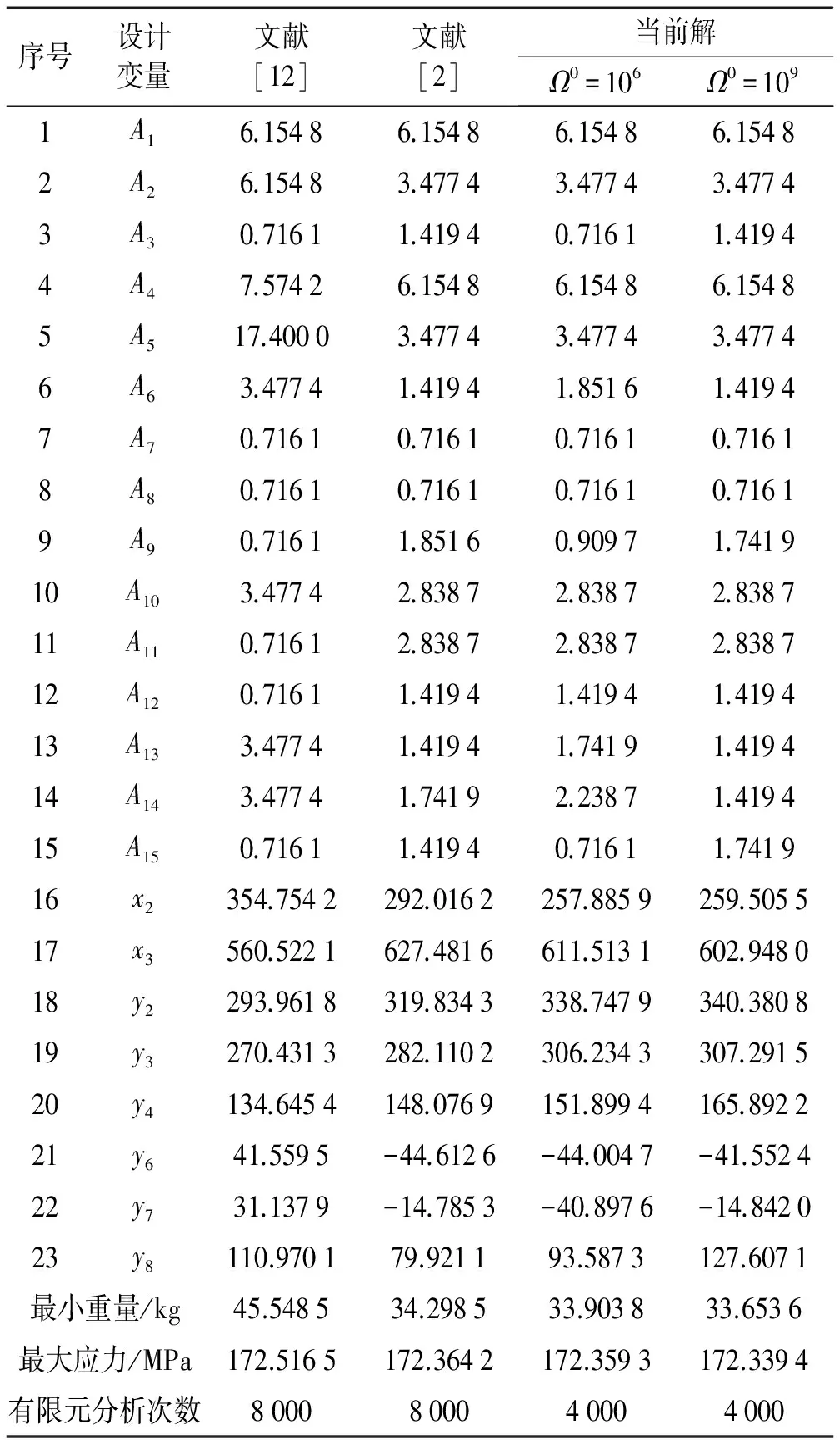
序號設計變量文獻[12]文獻[2]當前解Ω0=106Ω0=1091A16．15486．15486．15486．15482A26．15483．47743．47743．47743A30．71611．41940．71611．41944A47．57426．15486．15486．15485A517．40003．47743．47743．47746A63．47741．41941．85161．41947A70．71610．71610．71610．71618A80．71610．71610．71610．71619A90．71611．85160．90971．741910A103．47742．83872．83872．838711A110．71612．83872．83872．838712A120．71611．41941．41941．419413A133．47741．41941．74191．419414A143．47741．74192．23871．419415A150．71611．41940．71611．741916x2354．7542292．0162257．8859259．505517x3560．5221627．4816611．5131602．948018y2293．9618319．8343338．7479340．380819y3270．4313282．1102306．2343307．291520y4134．6454148．0769151．8994165．892221y641．5595-44．6126-44．0047-41．552422y731．1379-14．7853-40．8976-14．842023y8110．970179．921193．5873127．6071最小重量/kg45．548534．298533．903833．6536最大應力/MPa172．5165172．3642172．3593172．3394有限元分析次數8000800040004000

注：設計變量單位分別為A/cm2，x/cm，y/cm。

3.2 37桿平面桁架

37桿平面桁架初始結構見圖4。下弦自由節(jié)點均設有10 kg非結構質量。結構前三階頻率約束為：f1≥20 Hz;f2≥40 Hz;f3≥60 Hz。為保持結構對稱性，該問題含19個設計變量，即尺寸變量A1=A27，A2=A26，A3=A24，A4=A25，A5=A23，A6=A21，A7=A22，A8=A20，A9=A18，A10=A19，A11=A17，A12=A15，A13=A16，A14；形狀變量y3=y19，y5=y17，y7=y15，y9=y13，y11。材料參數、尺寸、截面設計約束見文獻[3]。

圖4 三十七桿平面桁架初始結構Fig.4 Schematic of the planar 37-bar truss

有限元分析最大次數設為8 000次。本文所得最優(yōu)設計見圖5。Ω參數自適應變化曲線見圖6。圖6顯示，在兩種參數設置下算法分別于第15代、第26代首次搜索到可行解。表明該算例為高難度優(yōu)化問題。本文方法與其它最優(yōu)解對比見表2。由表2看出，本文算法設計質量最優(yōu)、計算代價最小。

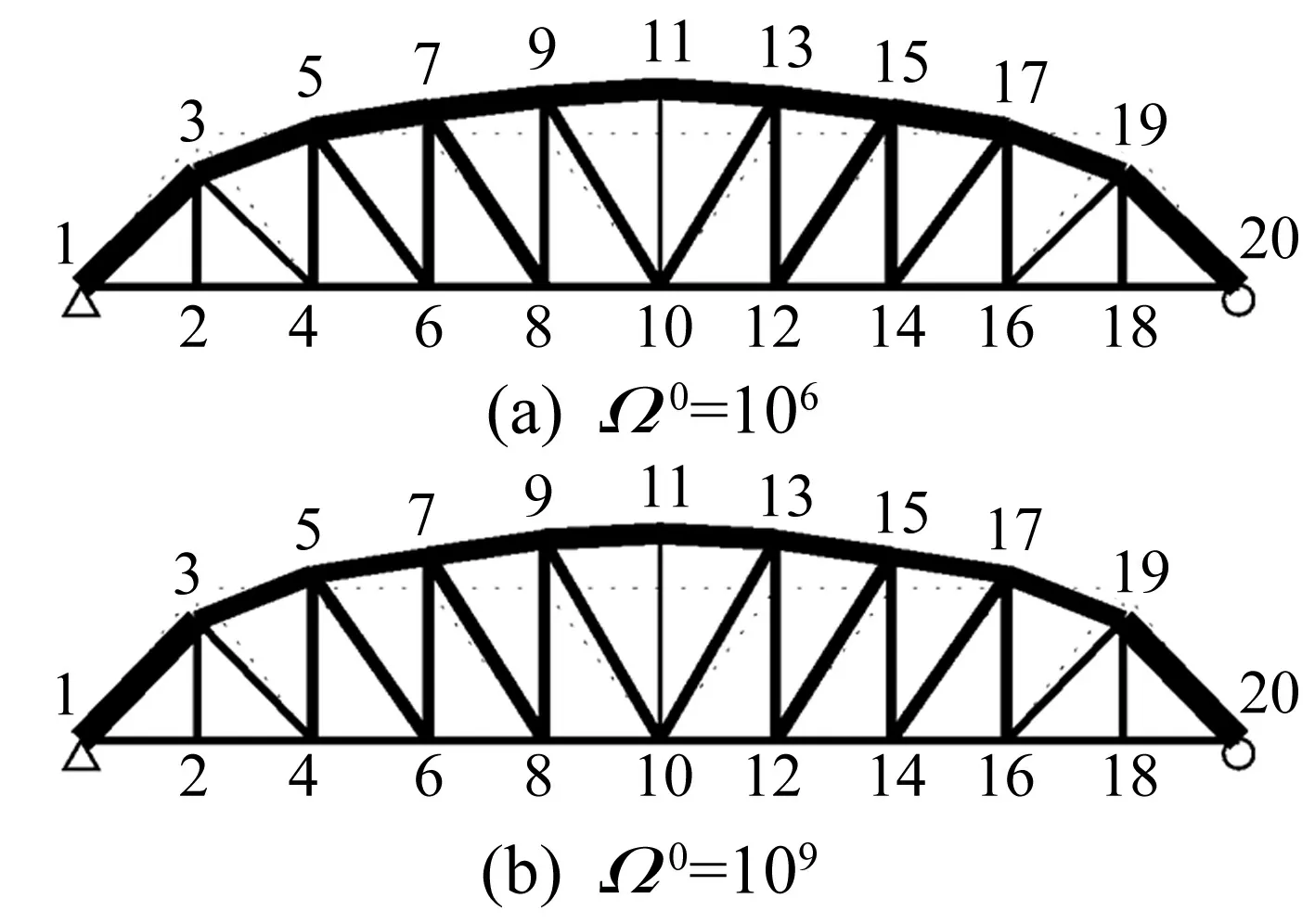
圖5 兩種參數初始值設置下37桿平面桁架最優(yōu)布局設計Fig.5 Best solutions of the planar 37-bar truss layout under two different cases of parameter initial value

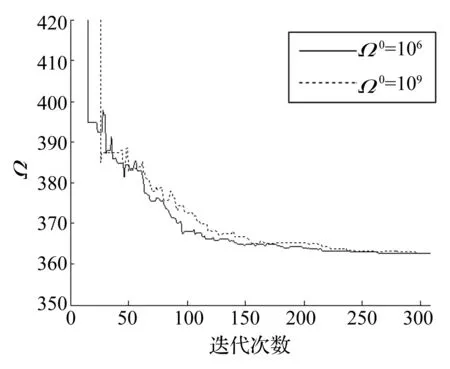
圖6 Ω參數變化曲線Fig.6 Variation curves of parameter Ω

3.3 72桿空間桁架

72桿空間桁架初始結構見圖7。桿單元許用應力區(qū)間[-172.369,172.369]MPa，節(jié)點許可位移區(qū)間[-0.6350,0.6350]cm。兩種工況下載荷分別作用于節(jié)點17與節(jié)點17、18、19、20。本文對經典算例進行拓展，分別采用兩種優(yōu)化方式處理，即僅考慮桿件截面、變量尺寸優(yōu)化問題及同時考慮兩類設計變量尺寸、形狀同步優(yōu)化問題。為保持結構對稱性，該問題含19個設計變量，即尺寸變量A1～A4，A5～A12，A13～A16，A17～A18，A19～A22，A23～A30，A31～A34，A35～A36，A37～A40，A41～A48，A49～A52，A53～A54，A55～A58，A59～A66，A67～A70，A71～A72；形狀變量y5～y8，y9～y12，y13～y16。材料參數及相關設計約束見文獻[4]。

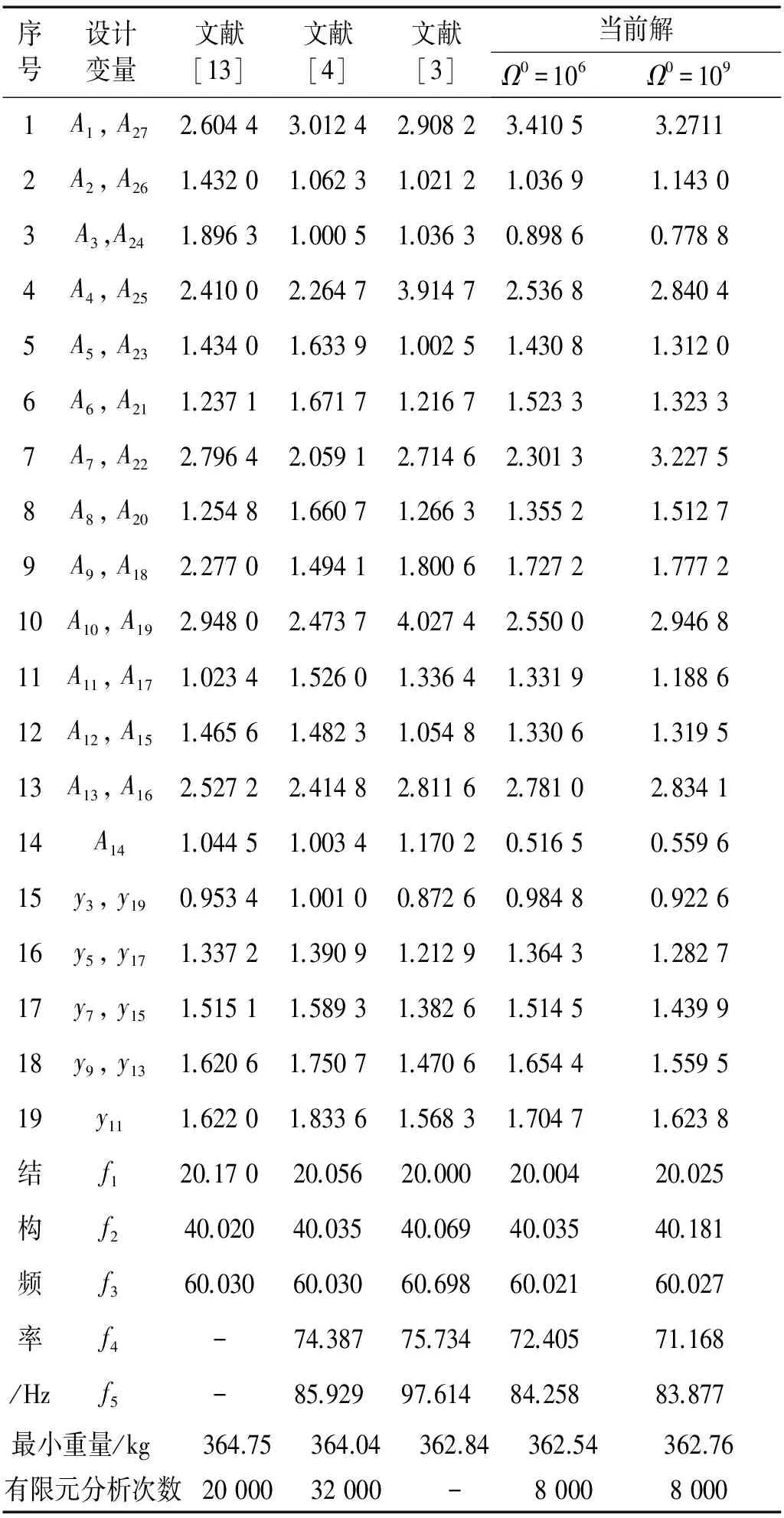
表2 37桿平面桁架布局優(yōu)化結果對比

注：設計變量單位為A/cm2、y/m。

有限元分析最大次數設為8 000次。在兩種Ω參數初始值設置情況下，分別求解尺寸優(yōu)化、尺寸與形狀同步優(yōu)化時，Ω參數的自適應變化曲線見圖8、圖9。本文方法與其它最優(yōu)解比較見表3。由表3看出，無論求解尺寸優(yōu)化或尺寸與形狀同步優(yōu)化問題，Ω-CMA-ES算法在獲得更優(yōu)設計的同時，均能極大減少結構重分析次數。

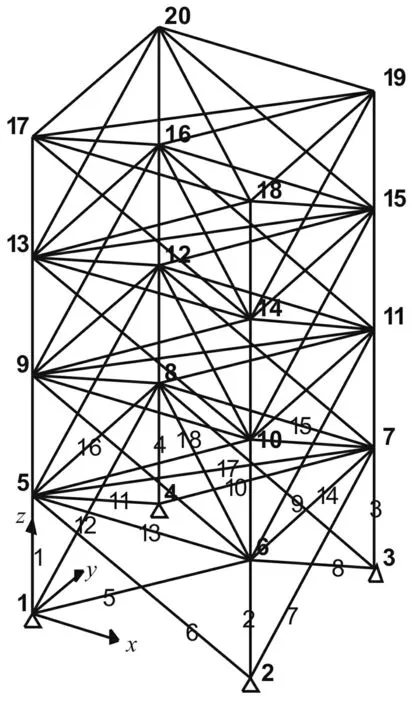
圖7 72桿空間桁架初始結構及桿節(jié)點編號Fig.7 Geometry and element definitions of the spatial 72-bar truss: node numbering scheme and element numbering pattern

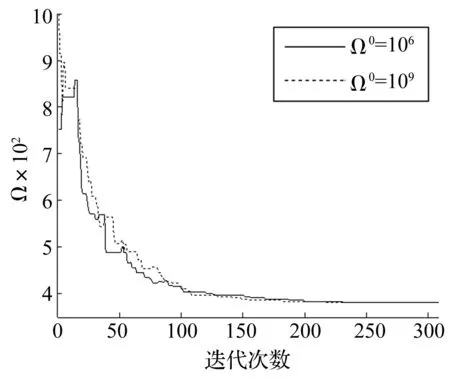
圖8 Ω參數變化曲線Fig.8 Variation curves of parameter Ω

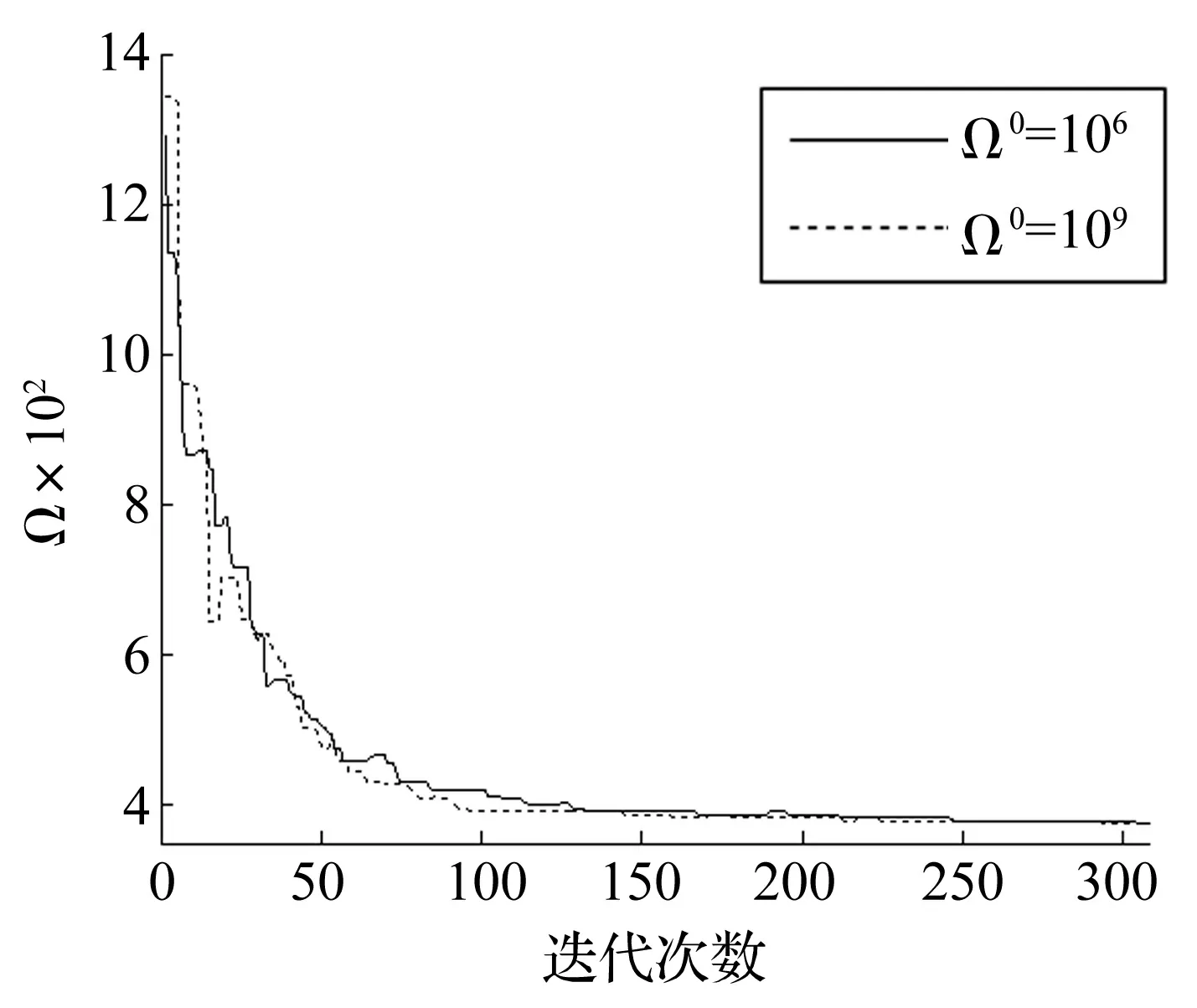
圖9 Ω參數變化曲線Fig.9 Variation curves of parameter Ω

表3 七十二桿空間桁架的優(yōu)化結果對比

Tab.3 Comparison of optimized designs found for the spatial 72-bar cantilever

序號設計變量文獻[14]文獻[15]文獻[16]文獻[4]當前解當前解Ω0=106Ω0=109Ω0=106Ω0=109尺寸優(yōu)化尺寸與形狀優(yōu)化1A1-A411．812011．693011．985011．848011．929012．736012．566012．75902A5-A123．23683．24973．26393．23933．41293．27813．16583．11683A13-A160．65610．64520．64520．64520．64580．64520．64520．64524A17-A180．66970．64520．64520．64770．64520．64520．64580．64585A19-A227．85038．73938．04908．07877．86268．21938．68268．83106A23-A302．73163．28323．39933．24773．31683．26393．21483．19297A31-A340．65480．64520．64520．64650．64520．64520．64650．64528A35-A360．64900．64520．65290．64650．64520．64520．64710．64589A37-A403．89293．46643．36063．69683．27423．27424．76004．736110A41-A483．54193．30523．33683．54773．42193．29683．21233．223211A49-A520．68320．64520．64770．64840．64520．64520．64580．645212A53-A540．64580．64520．64840．64580．64580．64580．65810．658713A55-A580．99941．00711．00971．01681．01101．01160．64520．645214A59-A664．17223．56713．55293．36903．53873．49873．56133．696115A67-A702．71482．75482．53032．81032．62062．53352．86582．786416A71-A723．90003．66643．82063．85293．50193．91553．73743．072317y5-y8------130．5588136．838918y9-y12------262．8435272．993919y13-y16------408．0970409．5308最大應力/MPa168．9747172．2663172．1339171．4092172．3669172．3538172．3387172．3580最大位移/cm0．63500．63470．63500．63470．63500．63500．63500．6350最小重量/kg174．7253172．5334172．4475172．7279172．4448172．4415169．6467169．6504有限元分析次數150004000019621190848000800080008000

注：設計變量單位分別為A/cm2，y/cm。

4 結 論

由于桁架優(yōu)化問題數值尺度及約束類型的多樣性，對每個問題尋找最合理算法參數值會得不償失，不具備實際工程意義。本文所提Ω-CMA-ES算法具有的兩特點為：

(1) 該算法僅一個Ω參數需人工設置。人工參數設置少并不等同于算法的可變參數少，而是算法能自動識別問題尺度，可在優(yōu)化進程中自適應調整相關算法參數，避免經驗參數設置的盲目性。

(2) 該算法具有較強的全局尋優(yōu)能力，且對Ω參數具備魯棒性。含平面桁架及空間桁架的3測試算例表明，Ω-CMA-ES算法可顯著降低有限元分析次數、有效提高設計質量，兩種Ω參數設置下最終優(yōu)化指標接近，且均優(yōu)于已有結果。

[1] 王棟. 結構優(yōu)化設計-探索與進展[M]. 北京: 國防工業(yè)出版社, 2013.

[2] Miguel L F F, Lopez R H, Miguel L F F. Multimodal size, shape, and topology optimisation of truss structures using the Firefly algorithm[J]. Advances in Engineering Software, Elsevier, 2013, 56: 23-37.

[3] Kaveh A, Zolghadr A. Shape and size optimization of truss structures with frequency constraints using enhanced charged system search algorithm[J]. Asian Journal of Civil Engineering (Building and Housing), 2011, 12(4):487-509.

[4] Kaveh A, Khayatazad M. Ray optimization for size and shape optimization of truss structures[J]. Computers & Structures, 2013, 117: 82-94.

[5] Runarsson T P, Yao X. Stochastic ranking for constrained evolutionary optimization[J]. Evolutionary Computation, IEEE Transactions on, 2000, 4(3): 284-294.

[6] Coello C A. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: a survey of the state of the art[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(11): 1245-1287.

[7] Bendsoe M P, Sigmund O. Topology optimization: theory, methods and applications [M]. Berlin:Springer, 2003.

[8] 程耿東, 顧元憲. 序列二次規(guī)劃在結構動力優(yōu)化中的應用[J]. 振動與沖擊, 1986, 5(1): 12-20. CHENG Geng-dong, GU Yuan-xian. Applications of SAP to structural dynamic optimization[J]. Journal of Vibration and Shock, 1986, 5(1): 12-20.

[9] Schlüter M, Gerdts M. The oracle penalty method [J]. Journal of Global Optimization, 2010, 47(2): 293-325.

[10] Jin Y, Olhofer M, Sendhoff B. A framework for evolutionary optimization with approximate fitness functions[J]. Evolutionary Computation, IEEE Transactions on, 2002,6(5):481-494.

[11] Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies[J]. Evolutionary Computation, 2001, 9(2): 159-195.

[12] 唐文艷, 袁清珂. 改進的遺傳算法求解桁架的形狀優(yōu)化[J]. 力學學報, 2006, 38(6): 843-849. TANG Wen-yan, YUAN Qing-ke. Improved genetic algorithm for shape optimization of truss structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(6): 843-849.

[13] 薛運虎,韋凌云,趙玫,等. 基于演化算法的帶頻率約束的桁架結構形狀和尺寸優(yōu)化[J]. 振動與沖擊,2010,29(12):13-17. XUE Yun-hu, WEI Ling-yun, ZHAO Mei, et al. Truss optimization on shape and sizing with frequency constraints based on evolutionary algorithms[J]. Journal of Vibration and Shock, 2010, 29(12): 13-17.

[14] 孟艷,趙洪波,茹忠亮,等. GEP在桁架結構優(yōu)化中的應用[J]. 工程力學, 2013, 30(1): 236-241. MENG Yan, ZHAO Hong-bo, RU Zhong-liang, et al. The application of GEP in truss structure optimization[J]. Engineering Mechanics, 2013, 30(1): 236-241.

[15] 李峰,唐和生,許銳,等. 桁架結構優(yōu)化設計的免疫克隆選擇算法[J]. 同濟大學學報:自然科學版,2010,38(9):1261-1265. LI Feng, TANG He-sheng, XU Rui, et al. Immune clonal selection algorithm for truss structure optimal design[J]. Journal of Tongji University:Natural Science, 2010,38(9): 1261-1265.

[16] Camp C V. Design of space trusses using big bang-big crunch optimization[J]. Journal of Structural Engineering, 2007, 133(7): 999-1008.

Novel constraint adaptive truss optimization approach

XIAO A-yang1, WANG Ben-li1, JIN Yao-chu2

1. Research Centre of Satellite Technology, Harbin Institute of Technology, Harbin 150001, China；2. Department of Computing, University of Surrey, Guildford GU2 7XH, United Kingdom)

A novel optimization algorithm by name Ω-CMA-ES, combining Oracle penalty function and metaheurastic algorithm was proposed to solve a typical multi-modal and highly non-linear problem, that is, the truss size and shape optimization. The algorithm can alleviate the cumbersome burden of parameters setting, and thus adaptively handle the constraints in truss design. Only one parameter Ω needs to be set manually while this algorithm is applied to handle various complex truss optimization problems. Numerical examples show the robustness of the proposed algorithm with respect to parameter Ω, for the algorithm can effectively handle various types of dynamic constrains, and the potential of the proposed algorithm in finding global optimal solution, for the relevant performance indicators are better than the results published in the literature.

truss optimization; Oracle penalty function; metaheurastic; constrained optimization; Ω-CMA-ES

2014-05-15 修改稿收到日期：2014-08-29

肖阿陽 男，博士生，1986年生

王本利 男，教授，1944年生

V414.19；TU323.4

A

10.13465/j.cnki.jvs.2015.14.033