基于迭代更新策略的快速高精度頻率估計方法

高志峰, 彭喜元， 彭 宇

1.哈爾濱工業大學 自動化測試與控制研究所，哈爾濱 150080；2. 山東大學 機電與信息工程學院，山東 威海 264209)

?

基于迭代更新策略的快速高精度頻率估計方法

高志峰1,2, 彭喜元1， 彭 宇1

1.哈爾濱工業大學 自動化測試與控制研究所，哈爾濱 150080；2. 山東大學 機電與信息工程學院，山東 威海 264209)

基于濾波器組的譜估計方法用于信號頻率估計頻率雖分辨率高,但濾波器組中心頻率格點劃分缺乏先驗知識，譜峰搜索過程存在計算復雜、信號不匹配問題。基于MVDR(Minimum Variance Distortionless Response)譜構造指標函數，將譜峰搜索問題等價為標量指標函數局部極小值問題求解，通過構造一組最速下降方向及自適應步長對極值頻率迭代更新，實現對信號頻率的直接估計。新算法不僅回避中心頻率點組劃分及傳統的譜峰搜索，且有效緩解信號不匹配，估計精度、計算效率更高。對單成分信號頻率估計精度與計算量進行新算法與現有算法的性能比較，并用于多成分信號頻率估計。

頻率估計；迭代算法；自適應步長；MVDR

信號頻率估計在機械振動信號監測及故障特征參數提取、電網狀態監測、雷達、通訊、語音信號識別等眾多領域占據重要地位[1-8]。頻率估計方法主要有參數化法及非參數法兩類。參數化方法假設信號滿足特定的數學模型，頻率分辨率更高，但模型失配時性能不佳且數學模型對相關參數初始值有諸多限制；而非參數化法無需建模應用更靈活，且可同時獲取頻率、幅值及相位等特征信息，但大多通過頻域譜峰搜索實現頻率估計，普遍存在計算量與估計精度的矛盾。如何快速、準確得到信號成分的頻率估計具有重要研究、應用價值。

最大似然估計(Maximum Likehood, ML)方法及非線性最小二乘(Nonlinear Least Square,NLS)方法可獲得最優信號頻率估計，但計算量巨大，且提高頻率分辨率需較長采樣序列。基于頻域的改進算法大多包含兩步，即采取快速離散傅里葉頻譜粗搜索提高計算效率，進而采取相位差法(Phase Different,PD)或迭代頻域細化搜索或頻域插值(frequency-domain interpolation)[9-10]法提高估計精度。在時域中通過信號建模可提高計算效率，包括基于線性預測(Linear Prediction,LP)模型及相位平均(Phase Average,PA)[11-14]。基于采樣數據自相關函數(autocorrelation-based)方法與基于迭代自回歸滑動(Autoregressive Moving Average，ARMA)模型[15]方法等。信號建模頻率分辨率較高，但大多屬于次優估計，在低信噪比時頻率估計性能不佳且存在模型失配問題。以上算法多適用于單頻率信號。

將短采樣數據上具有高分辨率的功率譜估計方法用于多頻率成分信號頻率估計[16-20]。基于協方差矩陣子空間分解的多重信號分類(Multiple Signal Classification, MUSIC)[16]及旋轉不變信號參數估計(Estimation of Signal Parameters via Rotational Invariance Technique,ESPRIT)[17]方法具有噪聲抑制能力，但其特征空間分解缺乏先驗知識，易造成空間維數判別失衡而得到有偏估計。基于匹配濾波組理論[18]的譜估計方法，利用一組均勻分割的頻率格點進行功率譜估計，并通過譜峰搜索實現。而預劃分頻率格點數目有限難以與信號頻率成分完全匹配，存在固有信號不匹配(Signal Mismatch Problem,SMP)問題[19]，包括最小方差無失真響應 (Minimum Variance Distortionless Response,MVDR)[20]及幅值與相位估計(Amplitude and Phase Estimation,APES)[21]等方法。理論表明傅里葉譜估計器也屬于匹配濾波器組譜估計方法[22]。基于預劃分均勻頻率格點的譜峰搜索，計算量與估計精度間存在固有矛盾關系。采取兩步式搜索實現頻率估計[23]：進行譜峰頻率粗搜索，采取二分法迭代搜索以提高估計精度緩解計算量，但粗搜索步驟所需計算量不可忽視。

本文提出基于迭代策略的譜峰頻率搜索算法，以回避傳統的譜峰搜索方式，在提高估計精度的同時降低計算量。基于MVDR譜定義標量指標函數，由指標函數極小值估計MVDR譜峰頻率。新算法基于最速下降法，由標量梯度函數構造一組迭代方向并計算最優更新步長，且迭代更新過程收斂到指標函數局部極小值。因無需預先劃分頻率格點，可緩解信號不匹配，且在頻率估計精度提高的同時降低計算量。新算法適用于單頻率信號，若結合初始頻率選擇策略，可直接推廣到多頻率信號頻率估計。在仿真、試驗中從精度、計算量角度對算法性能進行分析比較。

1 基于MVDR譜的頻率估計

含噪聲的時域采樣信號可近似為多成分正弦信號組合，即

(1)

式中：Ai,fi,φi分別為頻率成分幅值、頻率、初始相位；Ts為采樣周期；v(n)為加性高斯白噪聲。

則問題等價為通過MVDR譜峰角頻率ωi得到對信號時頻率fi的估計值fi=ωi/(2πTs)。

長度為N的采樣信號通過Hilbert變換轉換為復信號進行功率譜估計，其MVDR譜估計記為

(2)

式中：上標H表示共軛轉置；R為L維協方差矩陣；f(ω)為定義在角頻率ω∈[0,2π)的L維搜索向量，即

f(ω)=[1 e-jω… e-j(L-1)ω]T

(3)

式中：上標T表示矩陣及向量轉置運算。

若搜索向量f(ω)與信號x(n)頻率相同，則對應MVDR譜中的尖銳譜峰(局部極大值)。取式(2)分母作為指標函數，即

g(ω)=fH(ω)R-1f(ω)

(4)

則所有的MVDR譜峰均對應指標函數g(ω)的局部極小值點。本文采取最速下降方法構造g(ω)局部極小值頻率迭代式為

ωk=ωk-1-μkωg(ωk-1)

(5)

式中：μk為第k次迭代中正實數值步長；ωg(ωk-1)為指標函數g(ω)在角頻率ωk-1處標量梯度函數。

2 迭代頻率估計算法

2.1 梯度函數及自適應步長

搜索向量f(ω)關于角頻率ω的梯度函數定義為

[0 … -j(L-1)e-j(L-1)ω]T=-jJf(ω)

(6)

式中：J=diag([0,1,…,L-1])為常系數對角矩陣。

指標函數g(ω)關于角頻率ω的梯度函數定義為

jfH(ω)JR-1f(ω)-jfH(ω)R-1Jf(ω)

(7)

由jfH(ω)JR-1f(ω)=[-jfH(ω)R-1Jf(ω)]H簡化為

ωg(ω)=-2Im[fH(ω)JR-1f(ω)]

(8)

則頻率ωk上的梯度函數ωg(ωk)為實數值標量函數，且在局部極小值頻率上滿足)=0。

由式(4)、(5)知，最優迭代步長μk對應最小化問題

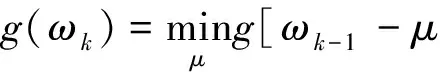
(9)

隨角頻率變量ωk迭代更新，函數g(ω)單調下降并收斂到局部極小值點。為獲得指標函數g(ω)閉式表達式，將指數函數ejmωk進行一階泰勒展開并線性化處理

e-jmωk≈e-jmωk-1-jme-jmωk-1(ωk-ωk-1)≈

e-jmωk-1[1+jmμkωg(ωk-1)]

代入式(3)得f(ωk)關于f(ωk-1)的近似表達式為

f(ωk)=(I+jμkωg(ωk-1)J)f(ωk-1)

(10)

式中：I為L維的單位對角陣。

將式(10)代入式(4)，得函數g(ωk)閉式表達式為

g(ωk)=fH(ωk-1)R-1f(ωk-1)-

jμkωg(ωk-1)fH(ωk-1)JR-1f(ωk-1)+

jμkωg(ωk-1)fH(ωk-1)R-1Jf(ωk-1)+

(11)

對步長μk求偏導，得梯度函數表達式為

μg(ωk)=-jωg(ωk-1)fH(ωk-1)JR-1f(ωk-1)+

jωg(ωk-1)fH(ωk-1)R-1Jf(ωk-1)+

(12)

將式(7)代入式(12)，得

(13)

由于Jf(ωk-1)為非零向量及逆矩陣R-1存在，則迭代步長μk均為正實數標量。

2.2 迭代算法和收斂性分析

由式(5)、(7)、(13)獲得指標函數局部極值的迭代求解算法(Single local minimum Iterative algorithm，SITER )，主要步驟為

步驟1: 起始角頻率ω0，Q=JR-1,U=JR-1J，k=1

步驟2: 由式(7)計算頻率點ωk-1對應的梯度函數

ωg(ωk-1)=-2Im[fH(ωk-1)Qf(ωk-1)]

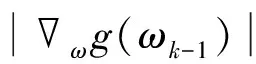
步驟3: 由式(13)計算迭代步長μk

μk=1/[2fH(ωk-1)Uf(ωk-1)]

步驟4: 更新頻率變量ωk=ωk-1-μkωg(ωk-1)，k=k+1，跳轉到Step2繼續執行。

證明：由式(5)及迭代步長μk>0，性質1自然成立。

證明：由式(4)，對可逆矩陣R, 指標函數g(ω)≥0為正值標量函數，存在下界。由式(9)獲得自適應步長滿足g(ωk)≤g(ωk-1)，即指標函數值單調下降。由式(11)得，當且僅當ωg(ωk-1)=0時等式成立g(ωk)=g(ωk-1)，即得到局部極小值點。

2.3 頻率估計解析解法

若信號中除噪聲外僅含單頻率成分，取矩陣維數L=2即可區分。由于此時指標函數g(ω)僅存在一個極小值點，可推導獲得頻率估計得解析表達式。記L=2維滿秩酉對稱協方差矩陣R及逆矩陣R-1分別為

(14)

式中：a22>0為正實數；a12=-r12/det(R),det(R)>0為矩陣R的行列式。

式(7)進一步簡化為

ωg(ω)=-2Im(fH(ω)JR-1f(ω))=

-2Im(a12e-jω+a22)=

-2{cosωIm(a12)-Re(a12)sin(ω)}

(15)

(16)

由a12=-r12/det(R), 可回避矩陣求逆運算，得

(17)

則單成分信號頻率可由式(17)直接求得，計算時間幾乎可忽略。式(17)為SITER算法在L=2的特例，不采取迭代過程，直接由(17)式獲得信號成分頻率估計 (Direct solution of the Iterative algorithm，DITER)。該算法僅適用于單頻率成分信號頻率估計，簡單易行，其頻率估計值常作為單成分信號時SITER算法迭代頻率初始值。

3 仿真實驗

3.1 單頻率成分信號的頻率估計

式(1)中頻率f=203.1 Hz，A=1，采樣長度32，采樣頻率fs=1 500 Hz，采樣周期Ts=1/fs。

DITER算法與Rife-ML方法及未加窗的線性預測(Kay-ULP)、相位平均(Kay-UPA)方法的均方誤差(Mean Square Error, MSE)隨輸入信噪比(Signal Noise Ratio, SNR)變化，并與Cramer-Rao Lower Bound (CRLB)比較見圖1。由圖1看出，Rife-ML方法基于周期圖譜峰搜索實現，驗證ML估計的最優性，但計算量繁重。而DITER、Kay-ULP、Kay-UPA算法性能接近，與CRLB存在約6 dB閾值，因數據截取時均未加窗導致頻譜泄漏，可加窗修正。DITER算法計算量少為優點所在。

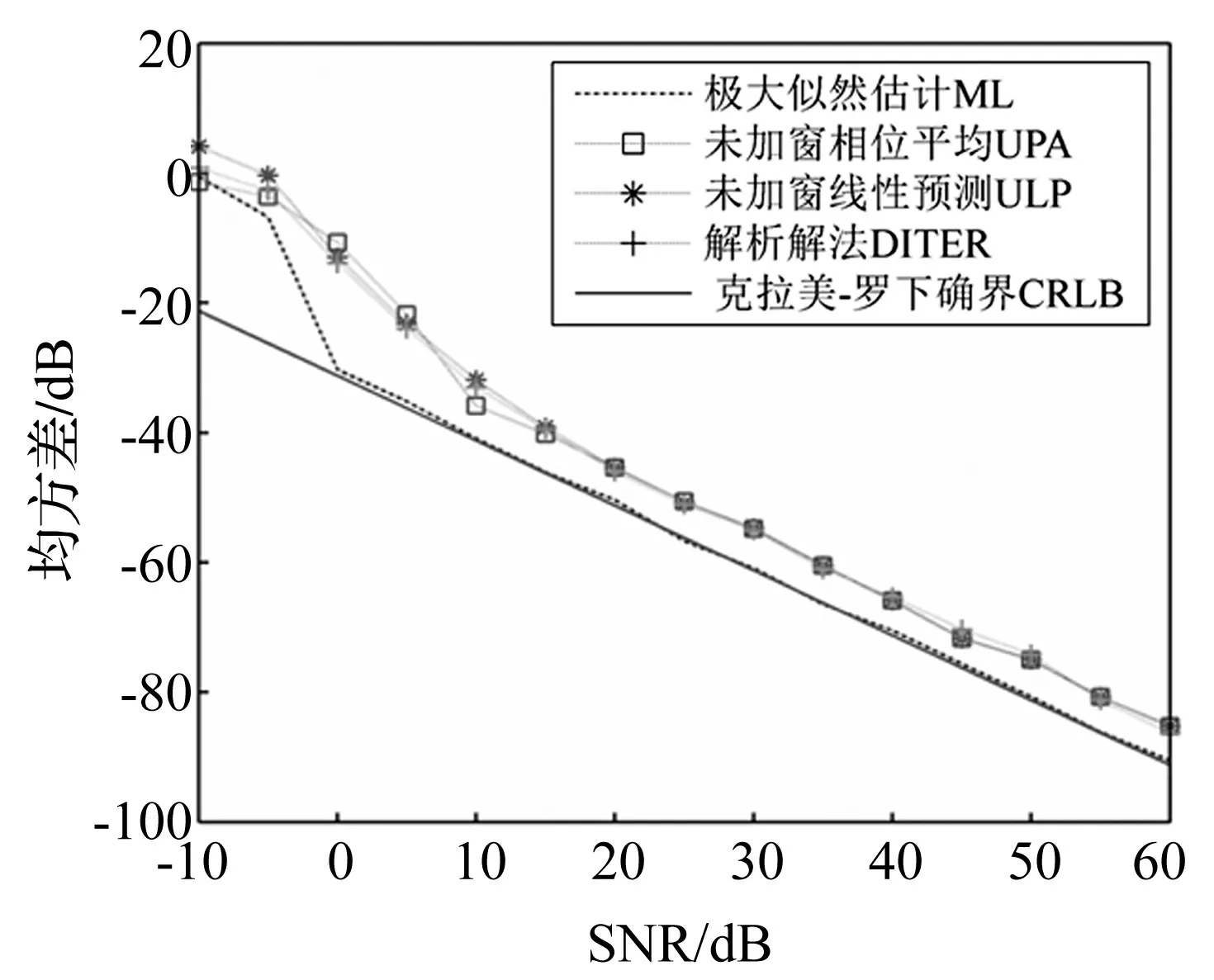
圖1 不同信噪比對應的均方誤差Fig.1 Mean square error versus different SNR

取L=2, SNR=40 dB，在K=200，2 000，3 000頻率格點的MVDR譜估計結果見圖2。由圖2看出，K越大頻率間隔越小，頻率估計精度越高，但計算量呈級數增加。圖2(d)為由式(17)直接所得DITER算法的頻率估計值，并由式(2)計算對應MVDR譜估計，其頻率估計最接近真實頻率203.1 Hz。

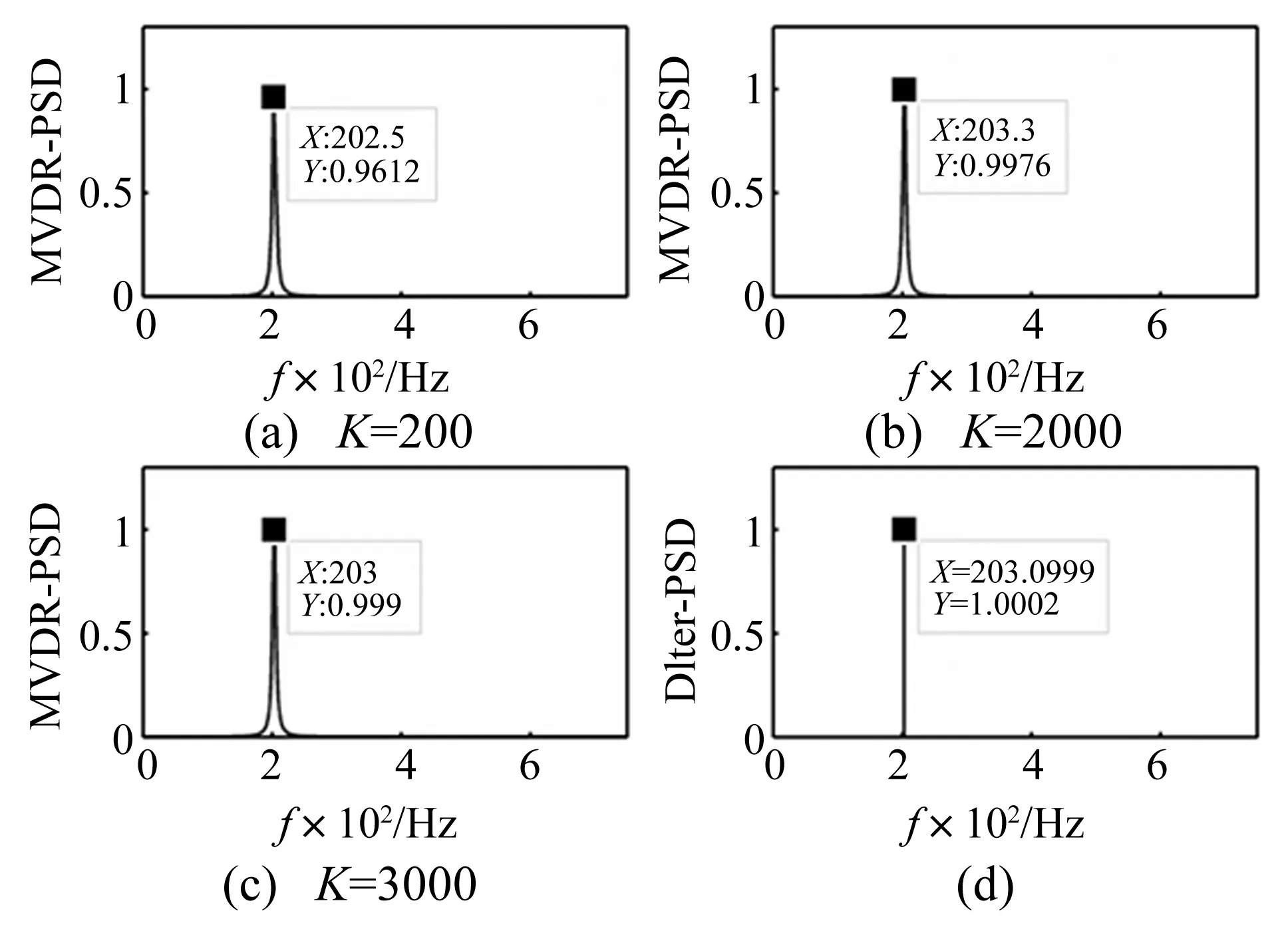
圖2 高信噪比時單頻率估計結果Fig.2 The frequency estimation with high SNR

不同信噪比及最大迭代次數對應的均方誤差見圖3。將矩陣維數增大L=8以獲取更高頻率分辨率及更窄匹配濾波器主瓣，提高估計精度。以DITER算法(L=2)的頻率估計值作為初始頻率, 用SITER算法進行迭代頻率更新。由圖3看出，隨SITER算法迭代次數增大(分別為3,5,10,100,200)，其估計值的均方誤差MSE越接近CLRB，頻率估計精度提高。

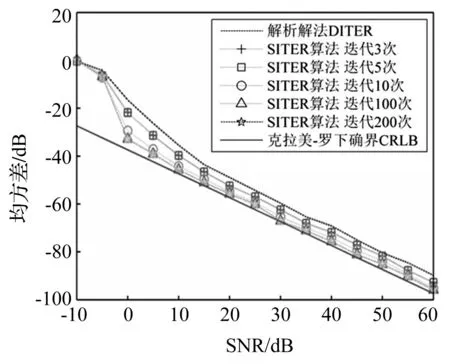
圖3 不同信噪比、最大迭代次數對應的均方誤差Fig.3 Mean square error versus different SNR and different maximum iterations

圖4為L=8及SNR=20 dB時，SITER算法不同迭代次數對應的計算量與MSE值，并與DITER算法(L=2)、標準MVDR算法(頻率格點數K=200, 2 000,3 000)進行比較(所有結果均為運行1 000次的平均值)。圖4(a)中SITER算法耗時與DITER算法相當，略少于K=200點的MVDR算法進行頻率估計及譜峰搜索所需時間；但圖4(b)中SITER算法的MSE遠小于其它結果，對應高估計精度。SITER算法打破了估計精度及復雜計算量間固有矛盾關系。

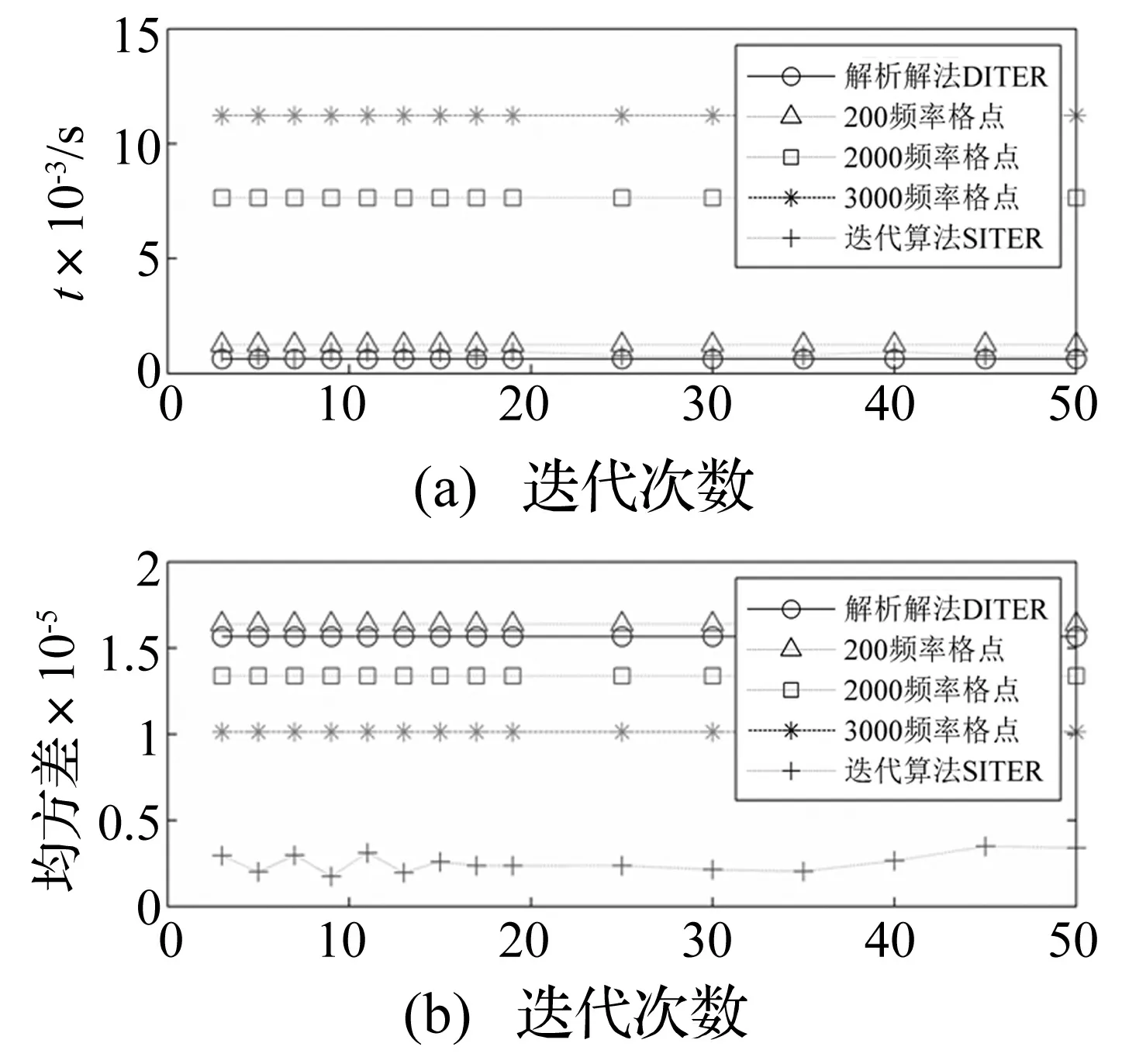
圖4 不同迭代次數對應的時間和均方誤差Fig.4 Time and mean square error versus iteration number

3.2 多頻率成分信號頻率估計

對含隨機噪聲的多正弦成分信號，有

式中：fi分別為各成分頻率{100,254,312,410,503}Hz；信噪比取20 dB, 連續采樣256點(采樣頻率1 500 Hz)，初始相位隨機φi∈[0,2π)，取協方差矩陣維數L=30。

MVDR譜分別在100，500，4 000個頻率格點的計算見圖5(a)、(b)、(c)。圖5(d)中共需獨立5次SITER算法以獲得5個信號頻率成分，對應的初始角頻率可采取傅里葉頻譜譜峰粗搜索獲得，或用MVDR算法在K=100頻率點上進行譜峰粗搜索獲得。

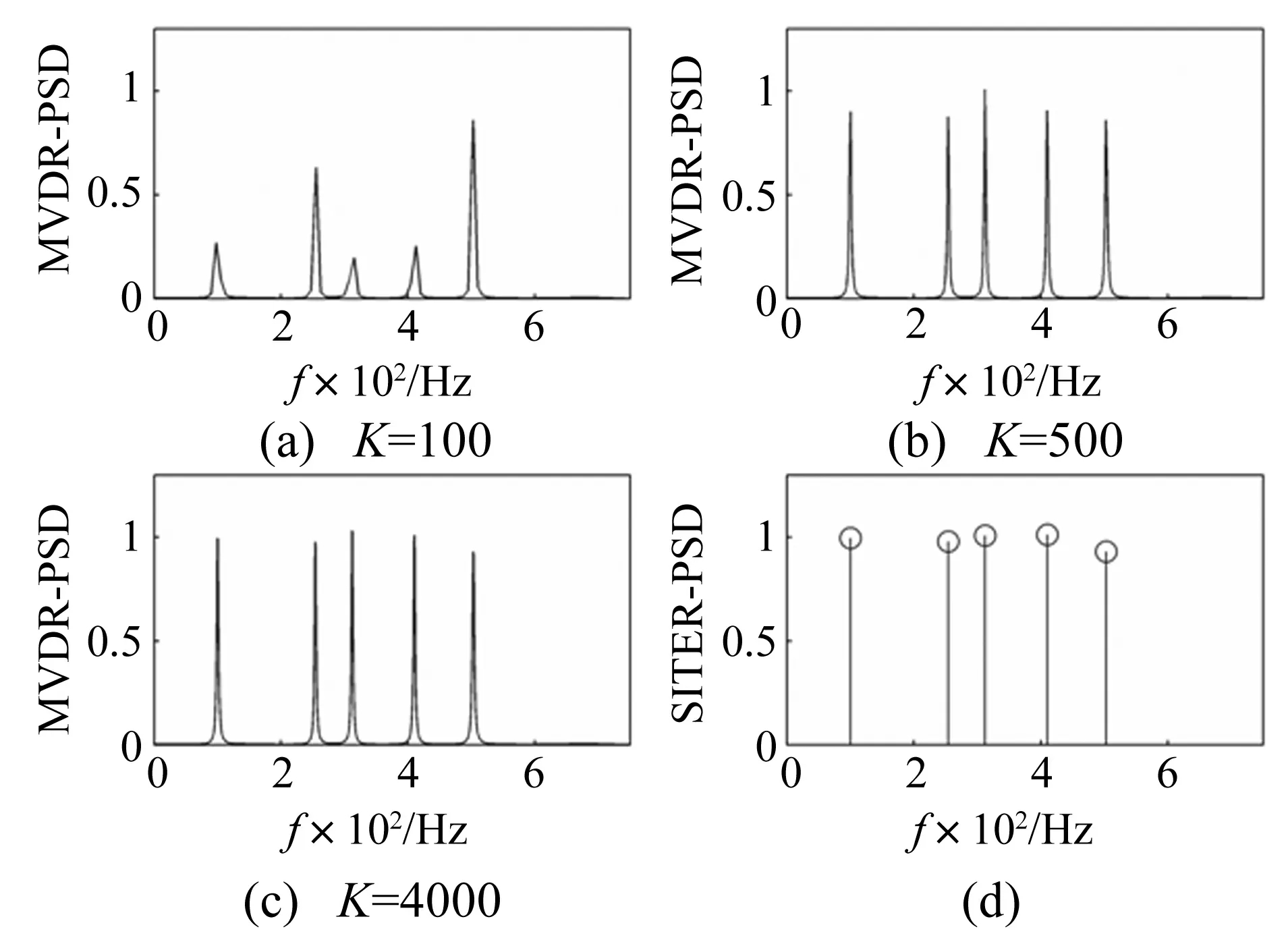
圖5 MVDR與SIter算法頻率估計Fig.5 The frequency estimations of MVDR and SITER algorithm

不同算法對應的頻率估計結果見表1。由表1看出，由SITER算法所得頻率估計精度優于MVDR算法在4 000個頻率點上所得頻率估計結果。

表1 不同算法對應的頻率估計結果

4 結 論

(1) 相對于低分辨率的傅里葉頻譜，匹配濾波器組譜估計方法在較短采樣數據上具有高分辨率。由于信號頻率成分數目、位置未知，傳統譜峰搜索方法普遍存在譜線不匹配(SMP)問題，估計精度及復雜計算量之間存在固有矛盾關系，影響估計精度的提升。

(2) 為提高頻率估計精度、降低計算量，提高計算效率，本文將譜峰搜索問題轉化為標量指標函數的局部極值計算問題，獲得局部極小值迭代算法SITER。最速下降搜索方向及最優步長的選取滿足指標函數單調下降，收斂到局部極小值點。針對單成分信號頻率估計，SITER算法簡化為解析算法DITER，無需迭代而直接計算信號頻率估計值。SITER算法推廣到多成分信號頻率估計應用中，可對多成分信號頻率估計算法有效補充。

(3) 在SITER算法中采取最速下降法，主要考慮其迭代收斂過程中指標函數值及頻率更新的單調性，但該方法收斂速度較慢，尤其在極值點附近。

[1] Stoica P, Moses R L.Spectral analysis of signals[M]. Pearson Prentice Hall, 2005.

[2] Li J, Stoica P. Roubust adaptive beamforming[M]. New York:Wiley, 2005.

[3] 胡愛軍,朱瑜.基于改進峰值搜索法的旋轉機械瞬時頻率估計[J].振動與沖擊,2013,32(7):113-117. HU Ai-jun, ZHU Yu. Instantaneous frequency estimation of a rotating machinery based on an improved peak search method [J]. Journal of Vibration and Shock,2013, 32(7):113-117.

[4] 沈廷鰲,涂亞慶,張海濤,等.一種改進的自適應格型陷波頻率估計算法及其收斂性分析[J].振動與沖擊,2013, 32(24): 28-32. SHEN Ting-ao,TU Ya-qing, ZHANG Hai-tao, et al.A modified frequency estimation method of adaptive lattice notch filter and its convergence analysis[J].Journal of Vibration and Shock,2013, 32(24):28-32.

[5] Rife C D, Boorstyn R R. Single-tone parameter estimation from discrete-time observations[J]. IEEE Trans. On Information Theory, 1974,20(5): 591-598.

[6] Stoica P, Nehoral A.Statistical analysis of two non-linear least squares estimators of sine waves parameters in the colored noise [J]. Proceddings of the ICASSP, 1998, 4:2408-2411.

[7] 胡文彪,夏立,向東陽,等. 一種改進的基于相位差法的頻譜校正方法[J]. 振動與沖擊,2012, 31(1): 162-166. HU Wen-biao, XIA Li, XIANG Dong-yang, et al. An improved frequency spectrum correction method based on phase difference correction method[J]. Journal of Vibration and Shock, 2012, 31(1): 162-166.

[8] Lin H, Ding K. Energy based signal parameter estimation method and a comparative study of different frequency estimators [J]. Mechanical Systems and Signal Processing, 2011, 25:452-464.

[9] Fu H, Kam P. Sample autocorrelation function based frequency estimation of a single sinusoid in AWGN[C]// Vehicular Technology Conference, IEEE 75th, 2012:1-5.

[10] Aboutanios E, Mulgrew B. Iterative frequency estimation by interpolation on Fourier coefficients[J].IEEE Trans. Signal Processing, 2005, 53:1237-1242.

[11] Jackson L, Tufts D, Soong F, et al. Frequency estimation by linear prediction[J].IEEE International Coference on Acoustics,Speech and Signal Processing,1978, 3:352-356.

[12] Kay S. A fast and accurate single frequency estimator[J]. IEEE Transaction on Acoustics,Speech and Signal Processing, 1989,37(12):1987-1990.

[13] Lui K, So K. Two-stage autocorrelation approach for accurate-single sinusoidal frequency estimation[J]. Signal Processing, 2008, 88(7):1852-1857.

[14] Cao Y,Wei G, Chen F. A closed-form expanded autocorrelation method for frequency estimation of a sinusoid[J]. Signal Processing, 2012, 92:885-892.

[15] Quinn B G, Fernandes J M. A fast efficient technique for the estimation of frequency[J]. Biometrika, 1991,78(3): 489-497.

[16] Schmidt R. Multiple emitter location and signal parameter estimation[C]// Proc. RADC spectrum estimation Workshop, 1979:243-258.

[17] Roy R,Kailath T. Esprit-estimation of signal parameters via rotational invariance techniques[J]. IEEE Trans. Acoust. Speech Signal Process., 1989, 37: 988-995.

[18] Stoica P, Jakobsson A, Li J. Matched-filter bank interpretation of some spectral estimators[J]. IEEE Trans. Signal Processing, 1998,66: 45-59.

[19] Cox H. Resolving power and sensitivity to mismatch of optimum array processors[J]. Journal of the Acoustic Society of America,1973, 54: 771-785.

[20] Benesty J, Chen J, Huang Y. A generalized MVDR spectrum [J]. IEEE Signal Process, 2005, 12(12): 827-830.

[21] Stocia P, Li H, Li J.A new derivation of the APES filter[J]. IEEE Signal Process, 1999, 6(8):205-206.

[22] Zheng C, Zhou M, Li X. On the relationship of non-parametric methods for coherence function estimation[J]. Signal Processing, 2008, 88:2863-2867.

[23] Peng Y, Gao Z, Peng X. MVDR spectral estimation by spectral peak dichotomous search[C]//I2MTC, 2012:1692-1696.

Fast and accurate frequency estimation with a gradient-based iterative algorithm

GAO Zhi-feng1, 2, PENG Xi-yuan1, PENG Yu1

1.Harbin Institute of Technology, Automatic Test and Control Institute, Harbin 150001, China;2.Shandong University, School of Mechanical, Electrical and Information, Weihai 264209, China)

Nonparametric spectral estimation algorithms were applied to frequency estimation for their significant performance. To avoid the signal mismatch problem and to improve the frequency estimation accuracy, a new iterative algorithm was presented based on the minimum variance distortionless response (MVDR) spectrum. With given initial frequency, searching directions and adaptive steps were derived to update the frequency sequence, which converges to a local spectral peak as the scalar gradient function goes to zero. Without the spectral peak searching on predefined analysis frequency grids, the computation is saved. The proposed algorithm was also applied to multiple component frequency estimation with carefully selected initial frequencies.

frequency estimation; iterative algorithm; adaptive step; MVDR

國家自然科學基金(61304142，61305130)

2014-04-17 修改稿收到日期：2014-06-03

高志峰 男，講師，1979年5月生

彭喜元 男，教授，1961年12月生

TP202.4

A

10.13465/j.cnki.jvs.2015.14.004