基于小波變換與Lipschitz指數的橋梁損傷識別研究

余 竹, 夏 禾, 殷永高， 孫敦華

1.北京交通大學 土木建筑工程學院，北京 100044; 2. 安徽省交通控股集團有限公司，合肥 230088)

?

基于小波變換與Lipschitz指數的橋梁損傷識別研究

余 竹1,2, 夏 禾1, 殷永高2， 孫敦華2

1.北京交通大學 土木建筑工程學院，北京 100044; 2. 安徽省交通控股集團有限公司，合肥 230088)

針對連續小波變換與Lipschitz指數在識別信號奇異性上的優越性，以裂縫模擬橋梁損傷，提出基于小波變換與Lipschitz指數的損傷識別方法。對損傷結構位移模態進行小波變換，用小波系數灰度圖及模極大值軌跡圖進行損傷定位，并用Lipschitz指數評價損傷程度。理論推導裂縫梁的Lipschitz指數范圍，并數值計算驗證該方法識別結構裂縫損傷的有效性。考察Euler梁及Timoshenko梁、不同程度損傷、多位置損傷、稀疏測點布置及噪聲測試等多種因素對損傷識別效果影響。

小波變換；Lipschitz指數；奇異性；損傷識別；位移模態

基于模態參數如自振頻率、振型的結構損傷識別方法頗受關注，皆因模態參數較易獲得并能較好刻畫結構整體性能。而從模態參數中提取局部信息如細微的缺陷卻并不容易。已有的基于模態參數損傷檢測方法均試圖尋找損傷與模態參數之關系。如Pandey等[1]用結構位移模態有限差分所得曲率信息識別損傷，將曲率模態用于梁式結構損傷檢測。Maia等[2]從位移頻響函數中推導出曲率頻響函數進而識別損傷。

小波變換在識別信號奇異性上優越性強[3]，損傷定位特性好且無需對測試數據微分。如Liew等[4-6]初步證實基于小波變換的結構損傷識別方法適用性。邱穎等[7]對結構健康、損傷狀態的模態曲率差進行小波變換,識別懸臂梁損傷，但該方法需結構未損傷信息。管德清等[8-9]對結構轉角模態或應變模態進行小波變換，用小波系數對彈性地基梁及框架結構進行損傷識別。趙俊等[10]利用移動荷載作用下簡支梁響應的小波系數識別出裂縫損傷位置。然而直接用小波系數識別小程度損傷較困難，且易受噪聲影響；而對損傷程度缺乏進一步評價。Hong等[11]用Lipschitz指數評價結構單損傷時損傷程度并進行實驗驗證。任宜春等[12]研究梁損傷位置與測點距離對Lipschitz指數影響。以上研究均未考慮多位置損傷工況及梁高深淺、測點疏密以及噪聲等因素對Lipschitz指數影響。而單純用某個尺度小波系數定位損傷存在缺陷，不易直觀研究各尺度的小波系數從而對損傷產生誤判。

為此，本文提出用含各尺度的小波系數灰度圖及小波系數模極大值軌跡圖對裂縫損傷進行直觀定位，并用Lipschitz指數評價損傷程度。考察Euler梁及Timoshenko梁的不同程度損傷、多位置損傷、稀疏測點及噪聲等因素對識別結果影響，并通過數值算例驗證該方法的適用性。

1 小波變換與Lipschitz指數

信號f(x)的連續小波變換可表示為

(1)

式中：ψ(x)為小波函數；ψ*(x)為復共軛；s，u分別為尺度、平移因子。

ψ(x)滿足容許條件為

(2)

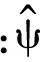
(3)

若小波函數ψ(x)滿足式(3)，則稱其具有n階消失矩。用連續小波變換計算的Lipschitz指數可用于評價信號的奇異性，Lipschitz指數定義如下：

信號f(x)在v處為Lipschitzα≥0當且僅當存在常數K>0及m次多項式pv(x)(m為小于α的最大整數)時，有

(4)

設n≥α，對式(4)第一式進行連續小波變換，并由消失矩定義考慮W[pv(u,s)]=0，得

W[f(u,s)]=W[ξv(u,s)]

(5)

Jaffard[13]已證明，如果平方可積函數f(x)在v處為Lipschitzα≤n, 則有

(6)

在x=v鄰域內，上式變為

(7)

其幾何意義為：小波系數的極大值位于沿尺度方向影響錐內。上式可化為對數形式，即

(8)

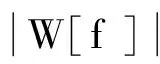
(9)

由Lipschitz指數定義不難看出，信號越不光滑奇異性越高，Lipschitz指數值越小。

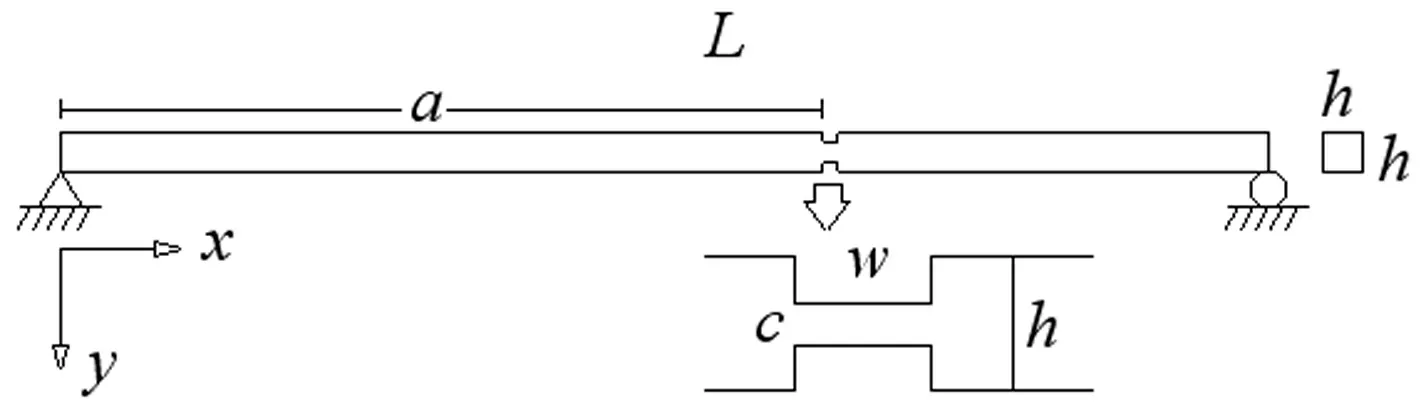
圖1 裂縫梁示意圖Fig.1 Sketch of a cracked beam

由圖1，對梁裂縫a處變形及內力(豎向位移、轉角、彎矩、剪力)平衡條件為

(10)

可見，裂縫梁位移模態在裂縫處存在一階導數但不連續。據分析，其Lipschitz指數范圍應為

1<α<2

(11)

本文選滿足消失矩條件的墨西哥帽小波(Mexican Hat Wavelet)作為母小波函數，表達式為

(12)

2 基于小波變換與Lipschitz指數的結構損傷識別

2.1 單一位置損傷識別

圖1中梁長L=1 200 mm,，彈性模量E=70 GPa，密度ρ=2 700 kg/m3，單元長度0.5 mm，共2 400單元；梁高h=20 mm，損傷位置梁高c=6 mm，c/h=0.3，損傷單元寬度w=0.5 mm，損傷位置距梁左端a=800 mm；采用梁單元用ANSYS進行有限元分析。裂縫處因截面高度h降低導致慣性矩I(矩形截面I=bh3/ 12)降低，故用抗彎剛度EI降低模擬裂縫損傷。以一階模態為研究對象，無、有損傷下梁的歸一化一階位移模態見圖2。由圖2可見，僅從位移模態幾乎看不出損傷位置有任何突變。

對損傷梁的位移模態進行小波變換(尺度s為64)后，所得各尺度的小波系數灰度見圖3，其中顏色越亮數值越大。由圖3看出，在損傷(800 mm)處有一條錐形亮條紋，小波系數在各尺度的模極大值位于此條紋內，由此式(7)獲得印證。

小波系數模極大值軌跡見圖4。由圖4看出，所有尺度的模極大值均指向800 mm損傷位置附近，對識別損傷位置非常有效。

小波系數模極大值與尺度的對數關系見圖5。由圖5可見，對數關系呈線性，從而式(8)獲得印證。用線性回歸方法計算擬合直線斜率并按式(9)求出Lipschitz指數為α=1.494 7，與式(11)吻合。

2.2 不同損傷程度識別

考察c/h=0.1、0.2、0.3、0.4、0.5、0.6、0.7七種不同損傷程度。對各工況的一階位移模態進行小波分析，其中c/h=0.1、0.3、0.5、0.7四種工況的小波系數灰度見圖6。由圖6看出，隨c/h增大損傷程度變小，損傷處錐形條紋由明變暗，因次可用錐形條紋明暗比較裂縫的損傷程度。

圖6 小波系數灰度圖Fig. 6 The contour plot of

對c/h=0.7工況，800 mm處損傷較難反映，考察各尺度的小波系數模極大值軌跡見圖7。由圖7看出，在前十幾個尺度上均能識別出損傷位置，但高尺度損傷信息被遮掩。

為研究其原因，以第6尺度為例，對比c/h=0.3及c/h=0.7兩種工況下小波系數，見圖8。由圖8可見，兩種工況的800 mm處峰值突變均指示出損傷位置。c/h=0.3工況因損傷較大，損傷處峰值既為極大值，亦為小段長距離內最大值，故而識別效果較好；但c/h=0.7工況因損傷較小，損傷處峰值僅為極大值，而非小段長距離內最大值，故而在灰度圖上亮度較周邊不明顯。盡管如此，對小損傷的c/h=0.7，就前十幾個尺度的結果而言，曲線在損傷位置仍有明顯峰值，說明該損傷識別方法有效。

計算各工況下Lipschitz指數見圖9。由圖9看出，隨c/h不斷增加Lipschitz指數不斷變大，符合Lipschitz指數檢測信號奇異性，因損傷越大信號越奇異，Lipschitz指數越小。

2.3 Timoshenko梁影響

算例梁高h=20 mm，高跨比1/60，屬于Euler梁。而Timoshenko梁的高跨比相對較高。為比較兩種不同高跨比簡支梁計算結果，將梁高增到h=240 mm, 即高跨比為1/5，寬度由20 mm增為100 mm。以c/h=0.3為例，損傷位置仍為800 mm，所得小波系數灰度見圖10。對比圖3的Euler梁計算結果看出，二者幾乎無差別，均識別出損傷裂縫位置。

分別計算Timoshenko梁在c/h=0.1～0.7幾種工況下Lipschitz指數，并與Euler梁計算結果比較，見圖11。由圖11看出，兩種梁損傷工況相同時Lipschitz指數基本相同，說明梁高的深淺對損傷裂縫處Lipschitz指數幾乎無影響，故可用于評價裂縫深淺。

2.4 多損傷位置的識別

仍以Euler梁為例(下同)，設梁在250 mm、500 mm、800 mm處單元損傷分別為c/h=0.5、0.6、0.3。小波系數灰度見圖12。由圖12看出，在每個損傷位置均出現亮條紋，且800 mm處損傷程度更大，條紋更亮。說明該方法對識別多位置損傷亦非常有效。

以第6尺度為例，其上小波系數見圖13。可見圖中每個損傷處的小波系數均出現極大值，且800 mm處峰值最大。

計算的小波系數模極大值軌跡見圖14。由圖14可見，對c/h=0.6 @500 mm及c/h=0.3 @800 mm處損傷, 小波系數模極大值識別出各損傷位置，而對c/h=0.5 @250 mm，雖尺度較大時識別結果發生偏移，但在前17個尺度上亦可正確識別出損傷位置。由于500 mm處損傷較250 mm處略小，故500 mm處損傷識別效果更好，因該處距跨中更近，對結構特性影響更大。

小波系數模極大值與尺度對數關系見圖15。分別計算各損傷位置的Lipschitz指數為

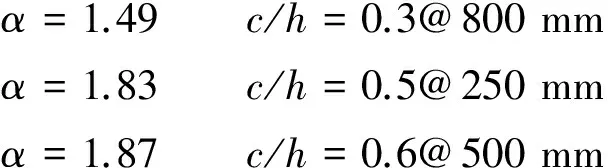
(13)

比較三處損傷的Lipschitz指數看出，在多損傷工況中亦能反映出損傷程度越小Lipschitz指數越大的規律，損傷也被有效識別。

2.5 測點稀疏布置影響

實測中因條件限制只能布置少量測點。而測點稀疏可能會影響結果。因此進行測點稀疏布置研究非常必要。

單損傷工況計算模型中，損傷區域寬度w=0.5 mm，測點間距d=w。在此基礎上加大測點間距，考察w/d=1/5及w/d==1/10兩種稀疏測點布置方式，在800 mm處單元損傷程度分別為c/h=0.1,0.2,…,0.7，取一階模態分析，小波變換尺度為64，所得不同測點間距的Lipschitz指數與損傷程度關系曲線見圖16。由圖16看出，隨測點間距增大Lipschitz指數不斷變大，因不充分的測點會漏失測點間某些奇異性損傷信息，使信號奇異性有所降低。

以c/h=0.3@800 mm為例，三種測點間距下小波系數灰度見圖17。由圖17看出，隨測點間距增加損傷處亮條紋逐漸模糊，且在較高尺度的損傷信息更易被掩蓋，但較低分解尺度上仍清晰可見。故該損傷識別方法對較稀疏測點布置仍有效。

算例中w/d分別為1, 1/5, 1/10，但損傷裂縫寬度較小(0.5 mm)，即使w/d=1/10, 也有241個測點。考察另一稀疏測點損傷，將損傷寬度增大為30 mm，此時w/d=1, 僅測量41個測點。將算例梁分為40個單元、41個節點，每個單元30 mm，損傷處位于第28單元(810～840 mm)，損傷程度為c/h=0.5。此時小波分解尺度為8，所得小波系數灰度見圖18，每個尺度上的小波系數極大值用黑點標示。由圖18看出，因測點稀疏，在灰度圖中形成諸多方塊。前幾個尺度上的小波系數極大值均位于810～840 mm范圍內，仍能識別出損傷位置。

計算出該工況下損傷處的Lipschitz指數為

α=1.47

(14)

2.6 噪聲影響

實測中需考慮測試噪聲影響。在前節稀疏測點模型基礎上，對一階模態添加信噪比SNR=25的Gauss白噪聲，見圖19。

噪聲存在時小波系數灰度圖、模極大值軌跡圖、模極大值與尺度對數關系分別見圖20～圖22，其中圖21、圖22為與無噪聲時的對比。計算出有噪聲時損傷處的Lipschitz指數為

αnoise=1.14

(15)

由圖20、圖21可見，即使存在噪聲，結構損傷仍可被識別，有無噪聲對損傷位置識別影響不大，二者都均在前4個尺度上識別出810～840 mm處損傷，說明該方法具有一定抗噪性。對比式(15)、(16)看出，添加噪聲的Lipschitz指數變小，此因噪聲本身有較大奇異性，能增大原信號的奇異性，從而使含噪信號Lipschitz指數降低；圖22中反映為含噪信號對應曲線斜率較小。

3 結 論

用本文所提方法對橋梁結構位移模態進行連續小波變換，用小波系數灰度圖及模極大值軌跡圖進行損傷定位，并通過Lipschitz指數評價損傷程度。考察Euler及Timoshenko梁、不同程度損傷、多位置損傷、稀疏測點及噪聲等多種因素影響，結論如下：

(1) 基于小波變換與Lipschitz指數方法可有效識別結構損傷；小波系數灰度圖、模極大值軌跡圖可直觀反映損傷位置，損傷程度可通過Lipschitz指數評價；裂縫損傷處的Lipschitz指數范圍1～2。

(2) 其它條件相同時，Lipschitz指數越小損傷程度越大；梁高深淺對損傷處Lipschitz指數幾乎無影響；增大測點間距，仍能夠準確識別損傷，且測點間距越大Lipschitz指數越大。

(3) 該方法具有一定抗噪性，且噪聲存在會使Lipschitz指數變小。

[1] Pandey A K, Biswas M, Samman M M. Damage detection from changes in curvature mode shapes[J]. Journal of Sound and Vibration, 1991, 145(2):321-332.

[2] Maia M M M, Silva J M M, Sampaio R P C. Localization of damage using curvature of the frequency response functions[J]. Proceedings of IMAC, 1997, 15(2):942-946.

[3] Sun Q, Tang Y. Singularity analysis using continuous wavelet transform for bearing fault diagnois[J]. Mechanical Systems and Signal Proceeding, 2002, 16(6): 1025-1041.

[4] Liew K M, Wang Q. Application of wavelet theory for crack identification in structures[J]. Journal of Engineering Mechanics, 1998, 124(2):152-157.

[5] Deng X, Wang Q. Crack detection using spatial measurements and wavelet analysis[J]. International Journal of Fracture, 1998, 91(2):23-28.

[6] Hou Z, Noori M, St. Amand R. Wavelet-based approach for structural damage detection [J]. Eng. Mech. Div., ASCE, 2000,126(7):677-683.

[7] 邱穎,任青文,朱建華. 基于小波奇異性的梁結構損傷診斷[J]. 工程力學, 2005, 22(S):146-151. QIU Ying, REN Qing-wen, ZHU Jian-hua. A beam damage diagnosis based on wavelet singularity[J]. Engineering Mechanics, 2005, 22(S):146-151.

[8] 管德清,黃燕. 基于轉角模態小波分析的彈性地基梁損傷識別研究[J]. 振動與沖擊, 2008, 27(5):44-47. GUAN De-qing, HUANG Yan. Damage identification of elastic foundation beams based on Wavelet Transform of rotating angle modes[J]. Journal of Vibration and Shock, 2008, 27(5):44-47.

[9] 管德清,黃燕. 基于應變小波變換的框架結構損傷識別研究[J]. 計算力學學報, 2010, 27(2):325-329. GUAN De-qing, HUANG Yan. Damage identification of frame structure by means of wavelet analysis of strain mode[J]. Chinese Journal of Computational Mechanics, 2010,27(2):325-329.

[10] 趙俊,張偉偉,馬宏偉.移動荷載作用下簡支梁的動態響應及裂紋損傷識別研究[J].振動與沖擊,2011,30(6):97-103. ZHAO Jun, ZHANG Wei-wei, MA Hong-wei. Dynamic response and crack detection of simply supported beam under moving loads[J]. Journal of Vibration and Shock, 2011,30(6):97-103.

[11] Hong J C, Kim Y Y, Lee H C, et al. Damage detection using Lipschitz exponent estimated by the wavelet transform: applications to vibration modes of a beam[J]. International Journal of Solids and Structrues, 2002, 39: 1803-1816.

[12] 任宜春,易偉建. 基于小波分析的梁裂縫識別研究[J]. 計算力學學報, 2005, 22(4):399-404. REN Yi-chun, YI Wei-jian. Crack identification by means of the wavelet analysis[J].Chinese Journal of Computational Mechanics, 2005, 22(4):399-404.

[13] Jaffard S. Pointwise smoothness, two-microlocalization and wavelet coefficients[J]. Publications Matemmatiques, 1991,35:155-168.

Bridge damage identification based on wavelet transform and Lipschitz exponent

YU Zhu1,2, XIA He1, YIN Yong-gao2, SUN Dun-hua2

1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044，China;2. Anhui Transportation Holding Group Co., Ltd, Hefei 230088, China)

The continuous wavelet transform and Lipschitz exponent perform well in detecting signal singularity. With the bridge damage modeled as a crack failure a damage identification method based on wavelet transform and Lipschitz exponent was proposed. With the wavelet transform applied to structural modal displacement, the damage can be located in the light of the contour plot and the locus of maximum modulus of wavelet coefficients. The range of Lipschitz exponent of cracked beams was derived theoretically. Some numerical examples show that the method can identify the damage effectively. Furthermore, some influential factors such as the effect of Euler or Timoshenko beam, different damage extent, multiple damage, sparse measuring points arrangement and test noise were studied.

wavelet transform; Lipschitz exponent; singularity; damage identification; displacement mode

國家自然科學基金(51178025)；國家重點基礎研究計劃973項目(2013CB036203)

2014-01-22 修改稿收到日期：2014-06-27

余竹 男，博士，1985年生

夏禾 男，教授，博士生導師，1951年生

O327

A

10.13465/j.cnki.jvs.2015.14.012