剖析試題背景 回歸問題本質

張軍

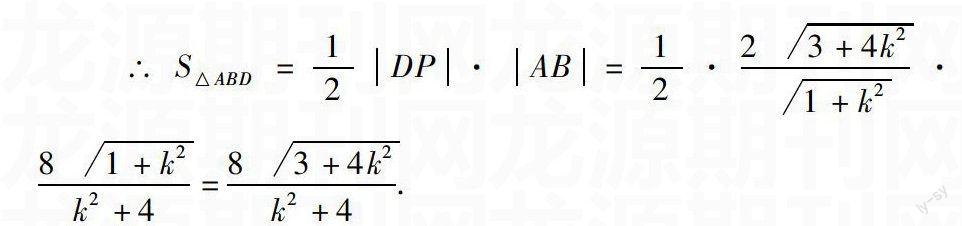
【摘要】在高三數學復習中，解析幾何題被認為是“一根很難啃的硬骨頭”，如何使得這根“硬骨頭”變得容易“啃”，而且要使學生“啃”得津津有味，甚至變成一道“美味佳肴”，這當然是我們高三復習要努力追求的.本文以2013年浙江高考理科數學卷21題為題源，通過對它的分析、設疑、求解、變式、拓展等教學環節進一步體現高考題這一寶貴的教學資源在教學中的潛在價值.

【關鍵詞】解析幾何；課堂教學；問題本質；思想方法

一、問題背景

經常會有學生反映：“老師，復習了那么長時間的解析幾何，做了那么多解析幾何試題，但是我現在還是很恐懼解析幾何，模擬卷的解析幾何題我都逼著自己嘗試著做，有時會做，有時一點思路都沒有，我該怎么辦呢？”在解析幾何的復習過程中，教師該如何帶領學生在制高點獲得突破？讓我們首先來看一例：

引例 （2013浙江理21）如圖，點P（0，-1）是橢圓C1：x2[]a2+y2[]b2=1（a>b>0）的一個頂點，C1的長軸是圓C2：x2+y2=4的直徑.l1，l2是過點P且互相垂直的兩條直線，其中l1交圓C2于A，B兩點，l2交橢圓C1于另一點D.

（Ⅰ）求橢圓C1的方程；

（Ⅱ）求△ABD面積取得最大值時直線l1的方程.

本題涉及橢圓的標準方程及簡單幾何性質，圓的標準方程及簡單幾何性質，直線方程，直線與圓相交弦長的計算，直線與橢圓相交弦長的計算，三角形面積的計算等，涉及內容豐富.第（Ⅱ）小題建立在第（Ⅰ）小題的基礎上，起點低，入口寬，層次遞進，由易到難，突出主干知識，緊扣考試說明.但是據統計，第（Ⅱ）小題得分并不高，究其原因，主要是解題方法選擇不當，運算能力不夠，最值求取存在問題，缺少知識的融會貫通和靈活運用.

那么如何高效地開展復習課教學，使學生學以致用呢？

二、案例操作

1.試題剖析

我們首先明確要求什么.題目要求我們求得三角形面積最大值時的直線方程，那么必須要得到三角形面積的表示.根據題意，我們能很快得到三角形的面積可以表示為S=12|DP|·|AB|.

那么怎么求呢？根據解析幾何的基本思想，利用代數來研究幾何，我們設法求出兩條弦長的代數式，涉及求解這個問題的三個關鍵點：直線方程、面積表示、面積的最大值.故可確定本題的解決方式大致如下：參數設定→方程及相關計算→等價轉化.

2.過程探究

萬事開頭難，教學中針對學生解題的薄弱之處——如何尋找解題的突破口，本題的分析過程從讀題、審題入手，重視對有效信息的提取、翻譯、加工、應用等環節的體現.通過幾個問題，將題目層層剖析，讓學生親歷問題分析的過程.

（Ⅰ）由已知得到b=1，且2a=4，∴a=2，所以橢圓的方程是x2[]4+y2=1.

（Ⅱ）（1）如何選取參數？

我們發現直線l1的位置一旦確定，整個圖像就確定了，而用代數來控制直線l1的就是它的斜率.因為直線l1⊥l2，且都過點P（0，-1），由題可得直線l1的斜率一定存在.這一步驟中借助圖形的幾何性質合理地分析出兩條直線的假設方式，既避免了分類討論，又沒有任何遺漏.考查了直線方程相關基礎知識，也通過這樣的步驟合理地設定了本題的參數.所以設直線l1：y=kx-1kx-y-1=0，則直線l2的方程為x+ky+k=0，目標量為S=12|DP|·|AB|，難度為分別求弦長AB和DP.

（2）題目中羅列的條件有哪些？

①l1交圓C2于A，B兩點；②l2交橢圓C1于另一點D.

（3）如何用代數的方法進行翻譯刻畫呢？

在合理假設直線方程的前提下，通過聯立方程，利用代數法可求得弦DP的長度，以及在圓中利用幾何法可求得弦AB的長度，這樣就可以順利寫出三角形ABD的面積表示.這里涉及解析幾何大題中的一些基本方法，如聯立方程、韋達定理、弦長等.

弦長AB根據直線與圓相交，利用垂徑定理求取得到關于斜率的一個函數d=1[]1+k2，AB=24-d2=23+4k21+k2.

DP則根據直線與橢圓相交，通過聯立方程組和弦長公式求得.由x+ky+k=0，

3.回歸本質

這個題思路簡單，采取的方法是通性通法.其實仔細分析每年高考題，我們會發現解析幾何的題具有很強的規律性，在每一題中總是若隱若現地出現那種看似無形卻有形、猶抱琵琶半遮面的情景，表達的精髓無非是坐標與方程，方程的核心則是直線方程，曲線方程往往是已知的.對直線方程，我們要有效地假設未知的信息，譬如引進斜率作為變量，通過直線與曲線方程聯立，結合韋達定理用設而不求的方式求解.總之，直線及其位置關系只有通過方程才能展開運算，只有運算才能對幾何關系進行有效的表達.

一堂課的內容是有限的，但對問題的研究是無止境的.在課堂講評之后，做以下變式，留作學生課后探究：

變式1：把橢圓改成拋物線y=2x2-6，點P（0，-2），l1，l2是過點P且互相垂直的兩條直線，l1交拋物線于A，B兩點，l2交圓于另一點D，求△ABD面積取最大值時直線l1的方程.

變式2：橢圓C1：x2a2+y2b2=1a>b>0和圓C2：x2+y2=b2，已知圓C2將橢圓C1的長軸三等分，且圓C2的面積為π，橢圓C1的下頂點為E，過坐標原點O且與坐標軸不重合的任意直線l與圓C2相交于點A，B，直線EA，EB與橢圓C1的另一個交點分別為P，N.

1.求橢圓C1的方程.

2.（1）設PM的斜率為t，直線l的斜率為k1，求k1t的值；

（2）求三角形EPM面積最大時直線l的方程.

三、教學反思

解析幾何是一門“方法論”色彩濃厚的學科，應當以“用坐標法研究問題”為主線，在教學過程中，向學生滲透函數與方程思想、數形結合思想、分類討論思想、等價轉化思想及運動變換思想.

（1）課堂教學應當“把時間還給學生，把方法教給學生”；

（2）課堂教學應當使學生的思維由“表層結構”向“深層結構”發展.

【參考文獻】

[1]洪昌強，胡小莉.回眸新課標下的浙江高考解析幾何解答題[J].數學通報，2014（4）：52.

[2]王連壩.5年高考3年模擬——高考理數[M].首都師范大學出版社，2014.

[3]晏良江.一道高考題的求解歷程[J].數學通訊，2012（11）.