淺析初中數(shù)學(xué)“證明直線是圓的切線”

陸浩杰

在初中數(shù)學(xué)教學(xué)中，相切是直線和圓的位置關(guān)系內(nèi)容的重中之重. 判定直線與圓是否相切是學(xué)習(xí)圓時經(jīng)常遇到的問題. 怎樣證明一條直線是圓的切線呢？現(xiàn)在我將介紹兩種常用的思路與方法：一是“連半徑，證垂直”，二是“作垂直，證半徑”.

一、“連半徑，證垂直”

當(dāng)直線與圓有明確的公共點時，連接該點和圓心，證明直線垂直于經(jīng)過這點的半徑.

例1 如圖1，已知AB為⊙O的直徑，點D在AB的延長線上，BD = OB，點C在圓上，∠CAB = 30°. 求證：DC是⊙O的切線.

思路 要想證明DC是⊙O的切線，只要我們連接OC，證明∠OCD = 90°即可.

【評析】 一定要分清圓的切線的判定定理的條件與結(jié)論，特別要注意“經(jīng)過半徑的外端”和“垂直于這條半徑”這兩個條件缺一不可，否則直線就不是圓的切線.

二、“作垂直，證半徑”

當(dāng)不能確定直線與圓有公共點時，則作圓心到直線的垂線段，證明圓心到直線的距離等于半徑長.

例2 如圖2，已知OC平分∠AOB，D是OC上任意一點，⊙D與OA相切于點E. 求證：OB與⊙D相切.

思路 連接DE，過D作DF⊥OB于點F，證明DE = DF即可. 這可由角平分線上的點到角兩邊的距離相等證得.

【評析】 一定要防止出現(xiàn)錯將圓上的一點當(dāng)作公共點而連接出半徑. 同學(xué)們一定要認(rèn)真體會證明切線時常用的這兩種方法，作輔助線時一定要注意表述的正確性.

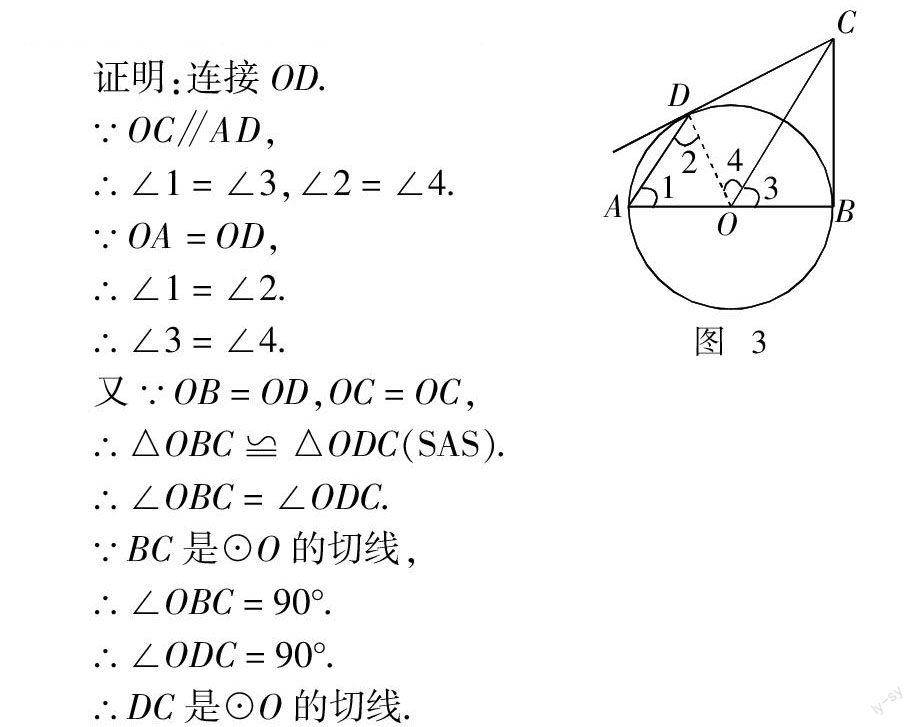
例3 如圖3，已知AB為⊙O的直徑，過點B作⊙O的切線BC，連接OC，弦AD∥OC. 求證：CD是⊙O的切線.

思路 本題中既有圓的切線是已知條件，又證明另一條直線是圓的切線. 也就是既要注意運用圓的切線的性質(zhì)定理，又要運用圓的切線的判定定理. 欲證明CD是⊙O的切線，只要證明∠ODC=90°即可.

【評析】 本題綜合運用了圓的切線的性質(zhì)與判定定理，一定要注意區(qū)分這兩個定理的題設(shè)與結(jié)論，注意在什么情況下可以用切線的性質(zhì)定理，在什么情況下可以用切線的判定定理. 希望同學(xué)們通過本題對這兩個定理有進(jìn)一步的認(rèn)識. 本題若作OD⊥CD，就判斷出了CD與⊙O相切，這是不對的， 這樣做相當(dāng)于還未探究、判斷，就已經(jīng)得出了結(jié)論，顯然是錯誤的.

綜上所述，我們可以看出，在證明一條直線是圓的切線時，往往需要添加適當(dāng)?shù)妮o助線. 添加輔助線的一般規(guī)律是：無點作垂線，有點連圓心.