中考一次函數經典易錯題型點撥

葉志華

【摘要】 一次函數及其圖像是初中代數的重要內容，也是高中解析幾何的基石，更是中考的重點考查內容. 其中有一些經典題型大家經常易犯錯的，因此筆者認為很有必要將一些關于一次函數常見錯誤的題型呈現出來.

【關鍵詞】 一次函數；圖像

首先總結一下一次函數的知識點.

1. 一次函數的定義

一般地，形如y = kx +b（k，b是常數，且k ≠ 0）的函數，叫作一次函數，其中x是自變量. ① k不為零，② x指數為1， ③ b取任意實數.當b = 0時，一次函數y = kx，又叫作正比例函數. 正比例函數是特殊的一次函數.

2. 一次函數的性質

簡單說，k是定向，b是定點.

k定向（定直線的方向），即k決定了直線y = kx + b與x軸正方向的夾角.

k > 0時，直線與x軸正方向的夾角是銳角，直線從左往右看呈上升趨勢，y隨x的增大而增大；

k < 0，直線與x軸正方向的夾角是鈍角，直線從左往右看呈下降趨勢，y隨x的增大而減小；

兩條直線k相同，則說明這兩條直線平行.

b定點，當x = 0時，y = b，因此一次函數y = kx + b的圖像經過（0，b），這個點恰好是圖像與y軸的交點. 常數項b就是直線y = kx +b與y軸交點的縱坐標.

3. 直線y = k1x + b1（k1 ≠ 0）與y = k2x + b2（k2 ≠ 0）的位置關系

4. 易錯題型分析

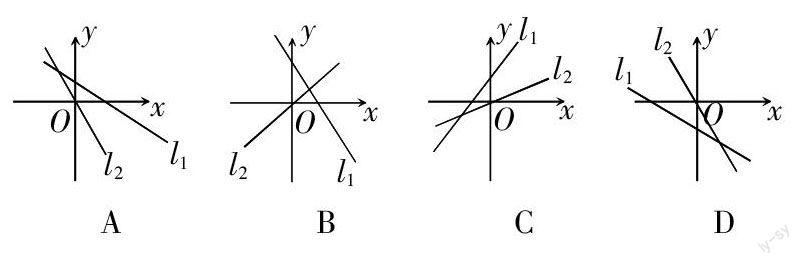
誤選A，不知道從何入手，本題可先分兩種情況考慮，可分為：① 當k > 2時，正比例函數圖像從左往右呈上升趨勢 ；一次函數的圖像從左往右呈上升趨勢，且與y軸交于正半軸，如選項C所示. ② 當0 < k < 2時，正比例函數圖像從左往右呈上升趨勢，一次函數圖像從左往右呈下降趨勢，且與y軸交于負半軸. ③ 當k < 0時，正比例函數從左往右呈下降趨勢，一次函數從左往右呈下降趨勢，且與y軸交于負半軸. 故正確答案為：C.

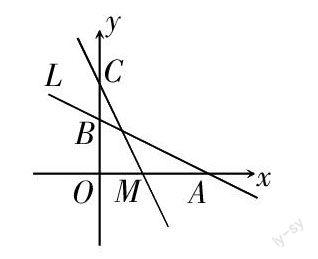
例9 如圖，直線L與x軸、y軸分別交于A，B兩點，在y軸上有一點C（0，4），動點M從A點以每秒1個單位的速度沿x軸向左移動.

（1）求A，B兩點的坐標；

（2）求△COM的面積S與M的移動時間t之間的函數關系式；

（3）當t為何值時△COM≌△AOB，并求此時M點的坐標？

分析：本題是動點問題，關鍵是抓住不變的等量關系.

（1）可先令x = 0，求出y = 2，從而得到B點坐標（0，2）. 再令y = 0，求出x = 4， 從而得到A點坐標（4，0）.

（2）∵ C（0，4），A（4，0），∴ OC = OA = 4，∴ OM = OA - AM = 4 - t.

∴由直角三角形面積得：S△OCM = 12OM × OC = 12|4 - t| × 4 = 2|4 - t|.

（3）分為兩種情況：

① 當M在OA上時，OB = OM = 2，△COM ≌ △AOB.

∴ AM = OA - OM = 4 - 2 = 2.

∴ 動點M從A點以每秒1個單位的速度沿x軸向左移動2個單位，所需要的時間是2秒鐘，M（2，0）.

② 當M在AO的延長線上時，OM = OB = 2，則M（-2，0），即M點的坐標是（2，0）或（-2，0）.

【參考文獻】

鮑敬誼.一次函數易錯題專講[ J].中學生數理化，2010（10）：28-29.