創設問題情境 激發學習興趣

林靜

現代認知心理學的研究表明，學生對學習內容的認知和學習效果的好壞，與其發生的情境有著密切的聯系，數學課堂教學中創設恰當的問題情境可以使學生與問題之間架設起一座“橋梁”，能喚醒學生強烈的求知欲望，增加學生學習數學的興趣，引導學生分析問題和探索問題，產生解決問題的動力和方法，促進學生全面地獲得數學知識.

那么如何創設問題情境，激發學習興趣呢？下面就如何創設問題情境，激發學習興趣談談個人的幾點感受.

一、直觀操作創設問題情境

美國教育家布魯納認為：“知識的獲取是一個主動的過程，學習者不應該是信息的被動接受者，而應是知識獲取的主動參與者.”新課程理念強調學生動手實踐、自主探究，讓學生親身經歷和體驗數學發現和創造的過程，發展學生的創新意識.

例如：在“分式方程”第二課時的教學中，我是這樣給學生創設情境的：

（一）解方程

（二）合作探究

為什么練習（2）中x = 2不是原方程的根？

1. 試比較練習（1）與練習（2），從解題步驟上來看，它們有差異嗎？

2. 你能說為什么用同樣的方法解分式方程，練習（1）有解，練習（2）無解？

（三）交流展示

1. 你認為在解方程中，哪一步的變形可能會產生增根？

2. 你能用較簡捷的方法檢驗求出的根是否為增根嗎？

這樣自然地讓學生理解解分式方程時為什么會出現增根，解分式方程時為什么要檢驗以及如何檢驗這些問題.

數學教學是學生數學活動的教學，通過學生的實驗操作等活動，學生可以加深對知識的理解、體會知識發展的來龍去脈、增強動手能力、提高思維水平.

二、巧用懸念創設問題情境

懸念情境能激發學生的好奇心，使學生欲罷不能，從而促使學生積極思考，主動探究.

懸念設置于課頭，可以一開始就激發學生強烈的求知欲. 例如：在學習“探索三角形全等的條件”時，我先讓學生學生思考如下兩個問題：

1. 調皮的小明用紙板擋住了兩個三角形的一部分，你能畫出這兩個三角形嗎？每個人畫出的三角形都全等嗎？

2. 粗心的小明不小心將一塊三角形模具打碎了，他是否可以只帶其中的一塊碎片到商店去，就能配一塊與原來一樣的三角形模具呢？如果可以，帶哪塊去合適？

教師因勢利導，引出要解決這兩個問題就必須認真學好這節課，這樣很自然地引入了新課，使學生在第一時間進入學習狀態.

懸念若設置于課尾，則有章回小說的效果. 例如在講了矩形的定義及性質一課后，可以給學生布置一道思考題：你要到玻璃店去劃一塊玻璃，只帶卷尺去，請問你怎么去檢驗這塊矩形玻璃是否標準？這就引出了下一課的矩形判定內容. 這樣就對學生的課外預習起了指導作用.

三、利用學生已有的舊知識來創設問題情境

心理學認為：學生在學習新知識之前，頭腦已經具有了某種認知結構，他總是試圖以這種原有認知結構來同化新知識. 因此在數學教學中，教師要從學生已有的知識出發，挖掘新舊知識的聯系點，創設問題情境.

如：探討“一元二次方程的概念”時，可以首先回憶舊知識“什么是一元一次方程”，然后提出問題，參照一元一次方程的概念，你能否講出一元二次方程的概念？并請學生舉例說明. 通過新舊知識對比，學生很容易地掌握了一元二次方程的概念.

又如：在學習分式的加減時可以先復習分數的加減，然后類比分數的加減法則得到分式的加減法則，建立起新舊知識之間的聯系，鞏固了舊知識的同時又掌握了新知識，增強了學生學習的信心.

四、利用直觀性圖形創設問題情境

數學之所以讓學生感到困難，主要原因就是數學的問題往往都比較抽象，如果能使抽象的問題具體直觀，就可以大大降低難度了. 所以在解決數學有關問題時，我們可以采用數形結合的方法，通過數形結合，使學生對問題有更深刻的理解和認識. 如：在解決函數的問題，特別是和函數的性質有關的問題時，我們一定要畫出函數的圖像，然后利用圖像來研究性質.

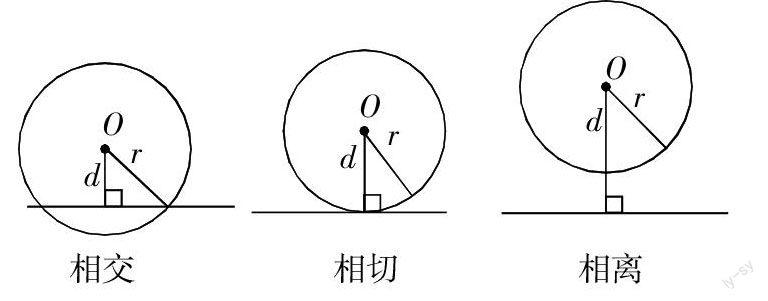
又如：在學習直線和圓的位置關系時，如果憑空說道理，學生是難以明白的，如果創設直觀性圖形情境，給出下圖：（其中d是圓心到直線的距離，r是圓的半徑）

五、利用多媒體教學技術創設問題情境

通過計算機多媒體創設問題情境，可以變靜態為動態，化抽象為直觀，充分調動學生感觀，使學生積極地參與教學過程. 如在學習一次函數的圖像和性質時，我設計用幾何畫板演示：當k值發生變化時，函數圖像的位置和函數的單調性會發生什么樣的變化？學生經過觀察，就能發現：當k > 0時，函數必過一、三象限，函數值隨自變量的增大而增大；當k < 0時，函數必過二、四象限，函數值隨自變量的增大而減小.

在幾何教學中，特別是幾何圖形運動的講授中，比如研究旋轉的性質時，就可用動畫演示：一條圖形繞一個定點（定點和圖形之間的位置分三種情況，即定點在已知圖形上、定點在已知圖形內、定點在已知圖形外）旋轉一定的角度，旋轉后得到的圖形和原圖形有什么關系？學生弄清了這個情境之后，就可以自己總結出旋轉的性質了.

總而言之，數學課堂教學是一個復雜的過程，最終目的是培養學生學習數學和運用數學知識解決問題的能力，創設問題情境只是一個教學的手段. 創設問題情境的方法也絕不止只是這幾種，只要我們掌握方法，注重情境創設的實效性和趣味性的有機結合，就能夠充分發掘學生的興趣點，調動學生學習的主動性和積極性，長期堅持下去，一定能達到學生想學數學，會學數學，并且能用數學的思維和方法看待問題和解決問題的能力的.