淺談課堂教學中學生數學思維培養取得點滴經驗

樸永梅

我國正在全面實施課程改革，課程改革是基礎教育的中心任務，是黨和國家的戰略部署，是實現高質量基礎教育的必經之路，是全面推進素質教育的核心內容，是牽動整個基礎教育改革與發展的系統工程. 數學作為重要的基礎課程對教育改革起著重要作用. 那么數學教育的改革最重要的是數學能力的培養. 數學能力的組成成分為：數學觀察力、數學記憶力、空間想象力、數學思維力、數學化能力，其中數學思維能力是數學能力的核心. 本文我將對中學生數學思維培養談談經驗和體會.

1. 重視問題解決

重視問題解決是各國和各地區數學課程目標的一個顯著特點. “具有解決數學問題的能力”是“數學素養”的一個重要標志. 數學解決問題的方式是先將問題可以用數或圖形呈現的形式，作出一些個案，然后以歸納的方式或演繹的方式，把個案的解法形成一個數學模式.

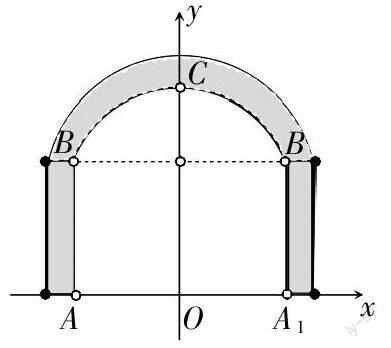
例如：如圖所示，是一條高速公路的隧道口在平面直角坐標系上的示意圖，點A 和A1、點B和B1分別關于y軸對稱，隧道拱部分BCB1為一條拋物線，最高點C離路面AA1的距離為8米，點B離路面為6米，隧道的寬度AA1為16米.

（1）求隧道拱拋物線BCB1的函數解析式；

（2）現有一大型運貨汽車，裝載某大型設備后，其寬度為4米，車載大型設備的頂部與路面的距離均為7米，它能否通過這個隧道？請說明理由.

2. 注重數學應用

注重數學應用是各國和各地區數學課程目標的一個突出特點，重視培養學生數學應用的能力，強調數學教學要與實際應用緊密聯系，教師幫助學生理解如何應用所學的概念與技能去解決問題，并形成系統的體系. 通過處理問題以及運用物質材料獲得數學知識和技能，提高理解能力，應用數學解決各種現實問題，易可從其他學科中提出數學問題，探索數學內容之間的聯系以及數學與其他學科之間的聯系.

例如：某女式鞋店的老板對去年一年的鞋的銷售量做了一個統計，發現女式鞋中，37、38號鞋賣的最好，34、40號鞋賣的最少，35、36、39號鞋賣的一般，并統計一下這些鞋不同鞋號銷售的百分比，通過上述統計，如果你是老板你在進貨的過程中將如何協調各鞋號之間的比例關系？問題處理的過程中，如果每個鞋號進貨量相同時可能會存在有的號脫銷，而有的號卻賣不了，要善于利用數據進行決策，處理生活中的問題.

3. 注重數學交流

數學在當今各學科中的用途急劇增加，究其原因重要的一個就是數學能簡明地表達和交流思想. 研究案例中以問答形式，通過討論分析，引導學生正確思維，培養學生分析問題和解決問題的能力.操作過程中也要根據學生的具體情況，采取多變的方式.學生配合得好，就以學生為主，學生回答問題不盡如人意時，教師就在提高語言、方式等方面多做文章，或以教師的講授為主. 交流有助于強化數學的思維，有效地組織思維活動，同時通過向教師和同學表達數學想法，并傾聽他人的數學表達，可以拓寬和豐富自己的數學知識. 有關數學概念和學習經驗、解決問題心得的交流，學生在經過整理和思考的基礎上，選擇恰當的描述和表達方式，呈現自己解決問題的思路、方法和結果的過程，包括反思與評價，是數學思想方法的交流.

4. 注重數學思想方法

受到數學思想的熏陶與啟迪，以此去解決所面臨的實際問題. 通過純數學知識的學習，使學生掌握數學的思想和方法，特別是一些具體的、技巧性較強的方法，如換元法、因式分解法、公式法等，通過解決實際問題使學生在掌握所要求的數學內容的同時，形成那些對人的素質有促進作用的基本思想方法，如試驗、猜測、模型化、合情推理、系統分析等. 研究案例中例2討論排列中常見的相鄰排列和分離排列問題，以及排除法、插空法等解法在應用中需注意的事項.

新課程改革刪減了一些比較“繁、難、偏、舊”的數學內容，例如代數式、方程與不等式、分式方程等降低了計算的要求. 不僅是因為計算機和計算器等現代信息技術的引入，更重要的是為了培養專門從事數學工作的學生而設置的數學，保持一定量的形式運算的同時，更重要的是關注運算的意義，《新課程標準》認為在重視恒等變形的同時，更應加強對運算概念的建立和對運算意義的理解，能夠根據題目條件尋求合理的、簡捷的運算途徑和計算方法.

方程思想是利用方程的知識方法解決問題的策略思想. 利用此思想方法解決問題，常規的思路是在實際問題中，撤開問題有關質的內容，將問題中的已知量與求知量抽象出來建立有關的等量關系，而后確定求未知數的值的思想. 但在數學教學中，常發現有些問題并非具備方程表面的特征，因此，在培養學生靈活應用方程思想的同時，可培養學生多角度思維的能力.

函數思想是從變量的角度處理問題的一種策略思想，它像一根主軸貫穿在中學數學知識的各個方面. 數學教學中若能滲透函數思想，不僅能培養學生思維的深刻性，而且能培養學生思維的創造性.