微積分實驗教學模式研究

程村

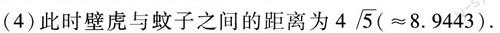
【摘要】針對高等院校經濟、管理等專業的微積分課程，設計了實驗教學方法.每個實驗案例都是從一個實際問題出發，來討論分析如何解決這個問題.一共設計了2個教學案例，每個教學案例基本上包括了“問題提出-建立數學模型-分析研討-計算機處理-思考”的過程.

【關鍵詞】實驗教學;案例教學;微積分

一、引 言

掌握簡單的數據處理方法，學會使用數學軟件解決數學問題;提高應用數學知識分析問題、解決問題的能力，掌握基本的數學建模方法和技巧，為將來的進一步的學習與工作打下一定的數學基礎.同時在教師指導下用學到的數學知識和計算機技術分析、解決一些經過簡化的實際問題，培養學生的數學興趣，從而進一步提高學生“用計算機做數學”的能力.

二、教學案例

案例一：蚊子和壁虎.適用教學內容：導數概念.可參考同濟大學《微積分（第六版）》【1】第二章第一節.

一、問題提出

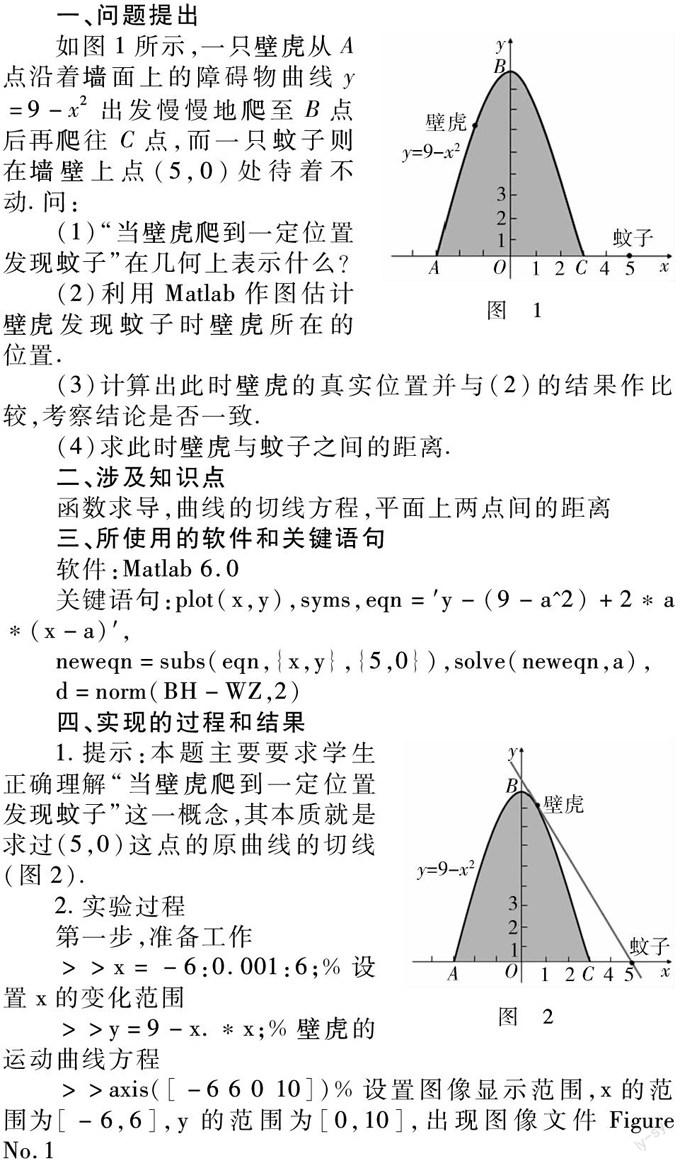
圖 1如圖1所示，一只壁虎從A點沿著墻面上的障礙物曲線y=9-x2出發慢慢地爬至B點后再爬往C點，而一只蚊子則在墻壁上點（5，0）處待著不動.問：

（1）“當壁虎爬到一定位置發現蚊子”在幾何上表示什么？

（2）利用Matlab作圖估計壁虎發現蚊子時壁虎所在的位置.

（3）計算出此時壁虎的真實位置并與（2）的結果作比較，考察結論是否一致.

（4）求此時壁虎與蚊子之間的距離.

二、涉及知識點

函數求導，曲線的切線方程，平面上兩點間的距離

三、所使用的軟件和關鍵語句

軟件：Matlab 6.0

關鍵語句：plot（x，y），syms，eqn=′y-（9-a^2）+2*a*（x-a）′，

neweqn=subs（eqn，{x，y}，{5，0}），solve（neweqn，a），

d=norm（BH-WZ，2）

四、實現的過程和結果

圖 21.提示：本題主要要求學生正確理解“當壁虎爬到一定位置發現蚊子”這一概念，其本質就是求過（5，0）這點的原曲線的切線（圖2）.

2.實驗過程

第一步，準備工作

>>x=-6：0.001：6;%設置x的變化范圍

>>y=9-x.*x;%壁虎的運動曲線方程

>>axis（[-6 6 0 10]）%設置圖像顯示范圍，x的范圍為[-6，6]，y的范圍為[0，10]，出現圖像文件Figure No.1

>>hold on;%在以上范圍內繼續畫圖

>>plot（x，y）;%畫出壁虎的運動軌跡

>>text（-2.5，8，′y=9-x^2′）;%在圖中適當位置加入文本信息，此處是加入曲線方程表達式得到圖3所示結果.

圖 3 第二步，在Figure No.1文件中的菜單欄找到Tools點擊其中的Edit Plot，然后用工具欄中的直線工具作出過（5，0）點的原曲線的切線，并找到切點不妨記為P，為了估計出P點的位置，作一條過P的垂線確定P的橫坐標約為1.08.

第三步，計算壁虎的真實位置.我們用理論

直接分析計算為：設切點坐標為（a， 9-a2），且切線在此點處的斜率為-2a，則切線方程應為y-（9-a2）=-2a（x-a），此切線方程過點（5，0），從而有0-9+a2=-2a（5-a），解得a=1或 a=9（不合題意舍棄）.這樣可得壁虎的真實位置為（1，8），它的橫坐標1與（2）中的估計值1.08接近.當然這一過程也可根據以上理論分析利用Matlab的符號計算功能實現如下：

>>syms x y a%設置x，y，a為符號對象

>>eqn=′y-（9-a^2）+2*a*（x-a）′%切線方程

運行結果：eqn=y-（9-a^2）+2*a*（x-a）

>> neweqn=subs（eqn，{x，y}，{5，0}）%切線方程過點（5，0）

運行結果：neweqn=-9+a^2+2*a*（5-a）

>>solve（neweqn，a）%解方程求出橫坐標a

運行結果：ans=[1]

[9]

此即上面分析得到的a=1或 a=9（妨上將后者舍棄）.

>>subs（′9-x^2′，1）%求出壁虎所在位置的縱坐標

運行結果：ans=8從而得到壁虎的真實位置為（1，8）.

第四步，求壁虎與蚊子間的距離，用兩點間距離公式求解，手算或Matlab均可.

手算為：d=（1-5）2+（8-0）2=80=45

Matlab數值計算為：

>>BH=[1，8];%壁虎的位置

>>WZ=[5，0];%蚊子的位置

>>d=norm（BH-WZ，2）%壁虎與蚊子間的距離

運行結果：d=8.9443與手算結果一致.

3.正確答案

（1）“當壁虎爬到一定位置發現蚊子”在幾何上表示曲線過點（5，0）且在ABC弧上的切線.

（2）利用Matlab作圖估計壁虎發現蚊子時壁虎所在位置的橫坐標約為1.08.

（3）壁虎的真實位置是（1，8）.

（4）此時壁虎與蚊子之間的距離為45（≈8.9443）.

五、問題延伸

1.給出壁虎的爬行速度及捕食速度，考察蚊子被捕食的時間.注意壁虎未發現蚊子時走曲線路徑（相當于要求計算曲線弧長），發現蚊子后捕食時走最短直線路徑.

2.進一步推廣到三維空間，就設想壁虎在二維曲面上運動，蚊子在xOy平面上不動，捕食過程同上，其中知識點將涉及求曲面的切平面，空間兩點間距離等.

案例二：草地面積的計算.適用教學內容：定積分在幾何學上的應用，可參考同濟大學《微積分（第六版）》第六章第二節.

一、問題提出

圖 4有一頭牛，被拴在一個半徑為r的圓形圍欄外﹙如圖4所示﹚.繩子的一端被固定在圍欄的A點，而牛能夠繞圍欄走到A點的對面B點.圍欄的外部都是草地，請問牛至多能吃到多大一塊面積的草？【2】

二、問題應用背景

通過研究草量與畜牧量之間的關系，建立牧場可持續發展方案.

三、涉及知識點

利用定積分求平面圖形的面積（直角坐標情形）.

四、解題思路

本題是求曲線所圍圖形的面積問題，學生需要通過分析找到曲線所圍的圖形，利用定積分來計算面積.在解題過程中，先要利用初等平面解析幾何的知識推導圓的漸伸線的參數方程表示形式，再進行計算.

圖 5五、解答過程

第1步，直觀分析曲線所圍圖形.

通過觀察，我們發現牛能吃到草的范圍是如圖5所示的陰影部分.

圖 6由題意知繩長為πr，而在A點左邊的區域是一個半圓面.至于剩下的區域怎么求得呢？當繩子纏住圍欄的時候，如圖6所示.牛所達到的最遠處為D，其弧AC與線段CD的長度之和為πr﹙繩子的長度﹚，而曲線即所有這種點所形成的軌跡.

第2步，利用初等平面解析幾何將D點軌跡描述出來.

取圍欄的中心為原點O，令OB與OC的夾角為θ﹙如圖﹚，于是C點坐標為（rcosθ，rsinθ），而CD是點C處圓的切線段，于是根據平面解析幾何的知識，有OC·CD=0，所以可設CD=k（sinθ，-cosθ），k>0為待定常數.而CD長度等于弧長BC的長度，于是|CD|=rθ，解得k=rθ.

圖 7所以D點坐標為：

（rcosθ，rsinθ）+rθ（sinθ，-cosθ）=（r（cosθ+θsinθ），r（sinθ-θcosθ））.

于是得到D點軌跡參數方程為

x=r（cosθ+θsinθ），

y=r（sinθ-θcosθ）.（0≤θ≤π）（*）

這剛好是圓的漸伸線，參見《微積分》（同濟六版上冊）287頁26題

第3步，分塊計算所圍圖形的面積.

我們先計算參數方程（*）下方圖形的面積S，如圖8中陰影部分所示.

圖 8 S=∫0πr（sinθ-θcosθ）d（r（cosθ+θsinθ））

=-∫π0r（sinθ-θcosθ）·rθcosθdθ

=-r2∫π0θsinθcosθdθ-∫π0θ2（cosθ）2dθ

=-r2[12∫π0θsin（2θ）dθ-∫π0θ2（1+cos（2θ）2）dθ]

=-r212∫π0θsin（2θ）dθ-12∫π0θ2dθ-12∫π0θ2cos（2θ）dθ

=-r212∫π0θsin（2θ）dθ-16θ3π0-14∫π0θ2dsin（2θ）

=-r212∫π0θsin（2θ）dθ-16π3-14（θ2sin（2θ）π0-

2∫π0sin（2θ）dθ）

=-r2∫π0θsin（2θ）dθ-16π3

=-r2-12∫π0θd（cos（2θ））-16π3

=-r2-12（θcos（2θ）π0-∫π0cos（2θ）dθ）-16π3

=16π3r2+12π2.

于是，由圖形的對稱性可得：

牛吃草的范圍=上下兩塊S+左半圓所圍圖形面積-圍欄所圍住的面積

=216π3r2+12π2+π（πr）22-πr2

=56π3r2.

3.結 語

數學實驗課是在我國大學中普遍開設的一門課程，對于它的具體實施方法，大家還沒有形成一個統一的模式，我們應當鼓勵各種不同模式進行試點和探索.但能夠肯定的有兩點：數學實驗是實驗課，應當以學生自己動手為主，而不是只靠學生聽課和看書接受數學知識;還有一點：數學實驗是要讓學生利用計算機來學習和應用數學知識.數學實驗課是微積分教學過程中必不可少的一個實踐性環節，開設數學實踐課是大學數學教學改革的進一步深入和延續，對于推進高等院校數學課程教學內容和課程體系的改革，培養學生具有解決實際問題的能力和創新精神，均會起到積極的作用.

【參考文獻】

[1]同濟大學數學系.《微積分（第六版）》高等教育出版社，2007

[2]James Stewart.Calculus：Concepts and Contexts，2 edition.Brooks/Cole Publishing Company，2000.Page 505.