人民幣匯率高階矩風險的持續性研究

■ 朱新玲，黎 鵬

一、引言

風險持續性是金融市場的重要現象，它表明當前風險不會在短期內消失，并會對未來風險的變化產生長期影響。風險的持續性實際上反映了市場信息流之間的相關性，信息流的相關程度越高，其表現出來的持續性越強。在外匯市場中，交易者的決策行為往往是基于從眾和自我判斷兩方面來實現的。從眾行為使得大眾交易者紛紛效仿優異交易者的投資行為，從而使他們的交易策略具有趨同性，而交易者根據自身經驗的自我判斷行為又會使他們采取不同的交易策略，進而使交易者之間的行為具有分散性。交易行為的趨同性和分散性使得外匯市場的風險時而收斂、時而發散，呈現出持續性特征。自從Engle和Bollerslev（1986）提出風險持續性概念以來，學者們對風險持續性進行了一系列研究。Nelson(1990)對GARCH模型的持續性進行了研究。Bollerslev和 Engle（1993）討論了向量 GARCH模型的持續性并提出了協同持續的概念，為分散波動持續性提供了解決思路。Jondeau(2003)對條件方差、條件偏度和條件峰度的存在性、持續性和協同運動進行了研究。樊智（2002）對中國股市數據的方差持續性和協同持續性進行了研究。李漢東（2002）研究了具有方差持續性的套利定價模型，指出方差的持續性會對長期投資的資產收益產生影響，進而影響資本資產的長期定價。李漢東（2003）探討了方差持續性的概念和性質，并分析了條件方差持續性對資本資產定價模型的影響。唐勇（2006）基于股票市場的高頻時間序列數據，從實證角度驗證了條件方差對資產定價的影響。蔣翠俠（2007）基于脈沖響應分析對股票市場的波動持續性和協同持續性進行研究，并提出了風險規避的策略。江孝感（2011）將持續性與變結構問題結合，運用向量MRS-GARCH模型對滬深股市波動持續性進行研究，證實滬深股市存在變結構的協同持續性。

縱觀國內外研究成果可以發現：（1）目前關于風險持續性的研究主要集中在方差持續性，對高階矩風險的持續性研究涉及較少。（2）當前的風險持續性研究以理論研究為主，實證分析較少。理論研究大多探討風險持續性及其規避策略、風險持續性對資產定價的影響、風險持續性對投資組合的影響等問題。（3）目前的風險持續性研究主要集中于股票市場，對于匯率市場研究涉及較少。

本文擬對人民幣匯率高階矩風險的持續性進行研究，以考察人民幣匯率高階矩風險的動態特征和變化規律，進而為外匯資產的組合配置和外匯風險規避提供理論基礎。

二、條件高階矩波動持續性的相關理論簡介

為了討論匯率序列條件高階矩風險的持續性，需先給出條件高階矩序列的波動持續性的相關概念。

（一）高階矩脈沖響應函數（MIRF）

對于N維向量隨機過程 ｛Yt｝，Ht為其條件方差－協方差矩陣，St為其條件偏度－協偏度矩陣，Kt為其條件峰度－協峰度矩陣，則方差脈沖響應、偏度脈沖響應、峰度脈沖響應分別定義為：

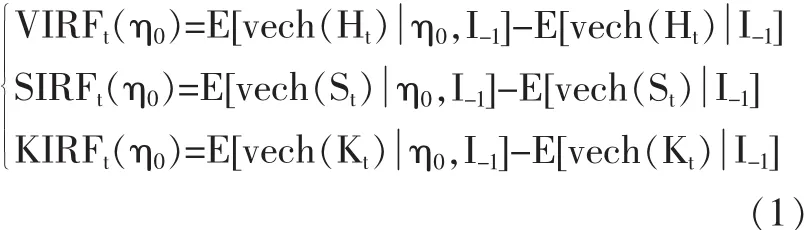
式（1）中 I-1為縮減的信息集，VIRFt（η0）為 ~N（H）=N（N+1）/2 維方差脈沖響應向量，SIRFt（η0）為~N（S）=N（N+1）（N+2）/6 維偏度脈沖響應向量，KIRFt（η0）為~N（K）=N（N+1）（N+2）（N+3）/24 維峰度脈沖響應向量。

（二）偏度持續

稱向量隨機過程 ｛Yt｝為偏度持續的，如果其偏度過程的脈沖響應函數滿足：

（三）峰度持續

稱向量隨機過程 ｛Yt｝為峰度持續的，如果其峰度過程的脈沖響應函數滿足：

（四）條件矩序列波動持續性判定定理

向量隨機過程 ｛Yt｝服從向量 GARCHSK（p1，q1；p2，q2；p3，q3）過程，若 ｛Yt｝的條件方差過程是單整的，則它是關于方差持續的；若 ｛Yt｝的條件偏度過程是單整的，則它是關于偏度持續的；若 ｛Yt｝的條件峰度過程是單整的，則它是關于峰度持續的。

三、人民幣匯率條件高階矩風險持續性的實證分析

（一）高階矩風險的持續性檢驗

為了檢測匯率波動高階矩風險的持續性，下面采用單位根檢驗分別對條件方差過程、條件偏度過程和條件峰度過程的單整性進行檢驗。具體的檢驗結果見表1、表2和表3。

表1 條件方差序列的單位根檢驗結果

從表1的檢驗結果可見，條件方差序列ht存在單位根，而其一階差分序列D（ht）是平穩的，即條件方差序列ht是一階單整的。根據條件矩序列波動持續性的判定定理可知，人民幣/美元名義匯率收益率序列的條件方差過程是關于方差持續的。

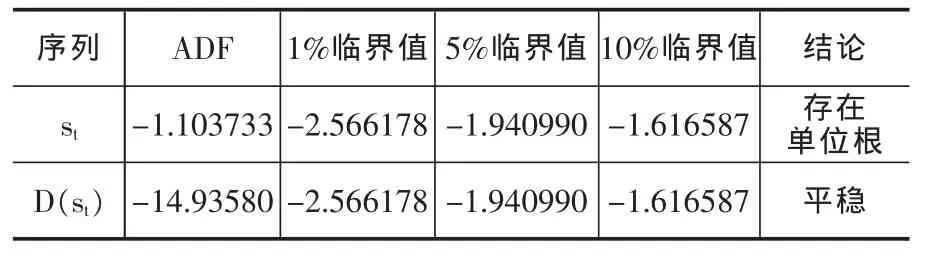
表2 條件偏度序列的單位根檢驗結果

從表2的檢驗結果可見，條件偏度序列存st在單位根，而其一階差分序列D（st）是平穩的，即條件偏度序列ht是一階單整的。根據條件矩序列波動持續性的判定定理可知，人民幣/美元名義匯率收益率序列的條件偏度過程是關于偏度持續的。

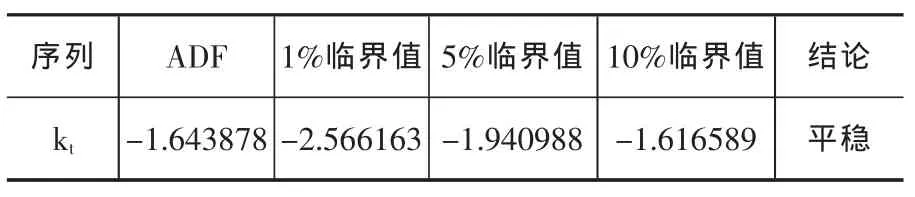
表3 條件峰度序列序列的單位根檢驗結果

從表3的檢驗結果可見，條件峰度序列kt在10%的顯著性水平下是平穩序列，即人民幣/美元名義匯率收益率序列的條件峰度過程關于峰度是非持續的。

（二）高階矩風險的持續期分析

匯率波動高階矩風險的持續性檢驗表明，人民幣/美元名義匯率收益率序列分別關于方差持續和偏度持續，而關于峰度是非持續的。為了進一步了解方差過程和偏度過程的持續期，下面分別對人民幣/美元名義匯率收益率序列的方差過程和偏度過程進行脈沖響應函數分析。

1.方差過程的脈沖響應分析

首先建立人民幣/美元名義匯率收益率序列方差過程VAR的模型，根據AIC和BIC準則，確定VAR模型的最佳滯后階數為1，因此建立VAR（1）模型，并做脈沖響應分析，以考察方差過程的持續性，表4給出了1～10階脈沖響應函數估計的系數值。

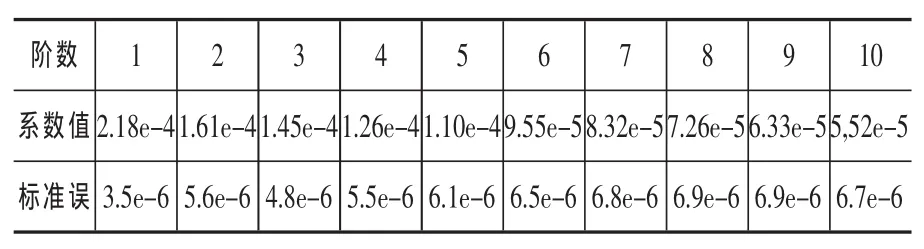
表4 方差過程脈沖響應函數系數值的估計結果

圖1是人民幣/美元匯率收益率序列的方差過程對一個標準差新息的脈沖響應函數圖，它更直觀地反映了隨機沖擊對匯率波動方差過程動態影響。

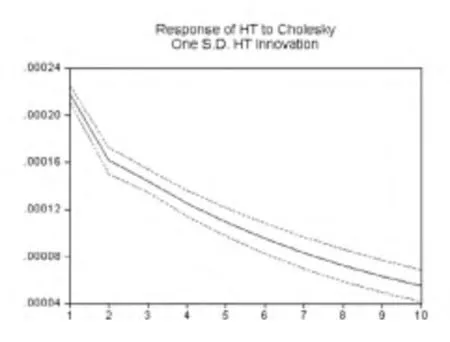
圖1 匯率收益率序列方差過程的脈沖響應函數圖

從圖1可見，對于某時刻方差過程一個標準差大小的隨機沖擊，人民幣/美元名義匯率收益率的波動在第2天迅速衰減，從第2～10天逐步衰減至0附近，到第10天這個隨機沖擊的持續影響基本消失。由此，方差過程一個標準差的隨機沖擊對人民幣/美元名義匯率收益率波動的影響大約在10天左右，也即人民幣/美元名義匯率收益序列方差過程的持續期大約為10天左右。

2.偏度過程的脈沖響應分析

首先建立人民幣/美元名義匯率收益率序列偏度過程的VAR模型，根據AIC和BIC準則，確定VAR模型的最佳滯后階數為1，因此建立VAR（1）模型，并做脈沖響應分析，以考察偏度過程的持續性，表5給出了1～10階脈沖響應函數估計的系數值。

表5 偏度過程脈沖響應函數系數值的估計結果

圖2是人民幣/美元匯率收益率序列的偏度過程對一個標準差新息的脈沖響應函數圖，它更直觀地反映了隨機沖擊對匯率波動偏度過程的動態影響。

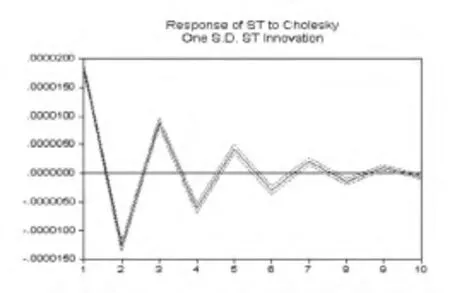
圖2 匯率收益率序列方差過程的脈沖響應函數圖

從圖2可見，對于某時刻偏度過程一個標準差大小的隨機沖擊，人民幣/美元名義匯率收益率在第2～6天起伏波動，第6～10天在0附近逐步震蕩衰減，且震蕩的幅度越來越小，到第10天這個隨機沖擊的持續影響基本消失。由此，偏度過程一個標準差的隨機沖擊對人民幣/美元名義匯率收益率波動的影響大約在10天左右，也即人民幣/美元名義匯率收益序列偏度過程的持續期大約為10天左右。

四、結論

（一）人民幣匯率的方差風險具有持續性，方差風險的持續影響會在10天內迅速消失。本文對方差過程進行單位根檢驗和脈沖響應函數分析，研究發現：人民幣匯率收益率的條件方差過程是一階單整的，即方差風險具有持續性特征；方差過程一個標準差的隨機沖擊影響在第2天開始迅速衰減，到第10天此隨機沖擊的持續影響基本消失。這表明方差風險是當前匯率市場交易者主要考慮的風險，投資者在決策時以方差風險最小為行為依據，進而匯率市場中方差風險信息流的相關程度較高，使得方差風險呈現持續性；鑒于投資者對方差風險均持最小化的態度，因此方差風險的影響在持續期內是迅速衰減的。

（二）人民幣匯率的偏度風險具有持續性，偏度風險的持續影響會在10天內震蕩衰減。本文對偏度過程進行單位根檢驗和脈沖響應函數分析，研究發現：人民幣匯率收益率的條件偏度過程是一階單整的，即偏度風險具有持續性特征；偏度過程一個標準差的隨機沖擊影響在第2～6天起伏波動，第6～10天以逐步縮小的幅度震蕩衰減到0附近。這表明偏度風險也是當前匯率市場交易者主要考慮的風險，由于偏度發生反轉的概率很大，即正偏度在未來變小的概率較大，負偏度在未來變大的概率較大，因此投資者在決策時偏好于歷史具有負偏度或較小偏度的投資，以期在未來獲得偏度反轉帶來的收益，這就使得偏度風險的影響在持續期內是起伏波動震蕩衰減的。

（三）人民幣匯率的峰度風險不具有持續性。本文對條件峰度過程進行單位根檢驗發現：人民幣匯率收益率的條件峰度過程是平穩序列，即峰度風險不具有持續性。這表明匯率市場的交易者對于代表極值損失的峰度風險是持規避的態度，交易者對峰度風險的規避行為使得匯率市場中峰度風險信息流的相關程度較弱，進而使得匯率市場的峰度風險不呈現持續性。

[1]Engle R F,Bollerslev T.Modeling the persistence of coditional variances[J].Econometric Reviews,1986,5(1):1～50.

[2]Bollerslev T,Engle R F.Common persistence in coditioanlvariance[J].Econometrica,1993,61（1）:167～186.

[3]Jondeau E,Rockinger M.Conditional volatility,skewness,and kurtosis:existence,persistence and comovements[J],Journal of economics dynamics and control,2003,27(1):1699～1737.

[4]樊智，張世英.金融波動性及實證研究[J].中國管理科學，2002，（6）：27～30.

[5]李漢東，張世英.具有方差持續性的套利定價模型研究[J].系統工程理論與實踐，2002，（6）：39～44.

[6]李漢東，張世英.存在方差持續性的資本資產定價模型分析[J].管理科學學報，2003，（1）：75～80.

[7]唐勇，張世英，張瑞峰.基于高頻方差持續的資本資產定價模型研究 [J].系統工程理論與實踐，2006，（10）：9～16.

[8]蔣翠俠.金融風險持續性及其規避策略研究[J].數學的實踐與認識，2007，（7）：13～22.

[9]江孝感，蔡宇.向量MRS-GARCH模型波動持續性研究[J].管理科學學報，2011，（8）：54～64.