菲涅爾面積分的計算

張思卿， 張新好， 黨寶軍， 李九凌

(1北京理工大學信息與電子工程學院北京100191 2中國人民解放軍94326部隊濟南250023)

引 言

Fresnel面積分是一個積分下限含有自變量的雙重復指數積分，無法通過直接求解得到。多年來，國內外學者提出了許多近似計算方法［1～4］，其中文獻［1，4］利用線積分的漸近展開式，給出了Fresnel面積分的近似計算，但其計算過程相當復雜、繁瑣，在對角度γ1、γ2分類的基礎上，還需對η值進行分類、判斷，不便于工程應用。本文對文獻［2，3］給出的Fresnel面積分計算公式進行詳細推導和分析，基于Jacobi-Anger恒等式和Bessel函數的性質，提出了一種新的Fresnel面積分近似計算公式，并與文獻［3～5］的結果進行對比驗證。

1 Fresnel面積分的類型

由文獻［6］可知，雙雷達柵多路徑傳播損耗模型中的八個場分量，均含有Fresnel面積分

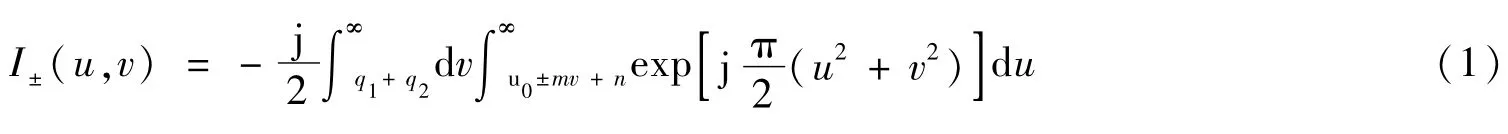
式中，q1、q2、u0、m和n均為實常數。I下標的正負號與m的正負號相對應，其分類及計算公式見表1。

令

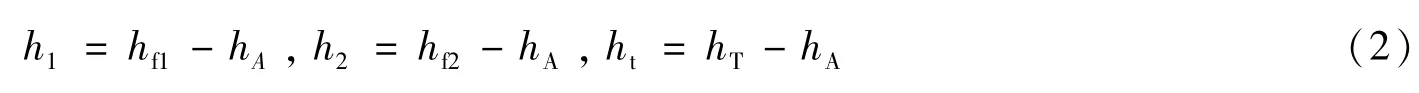
式中，hf1為第一個雷達柵的高度，hf2為第二個雷達柵的高度，hA為天線的高度，hT為目標的高度。

則

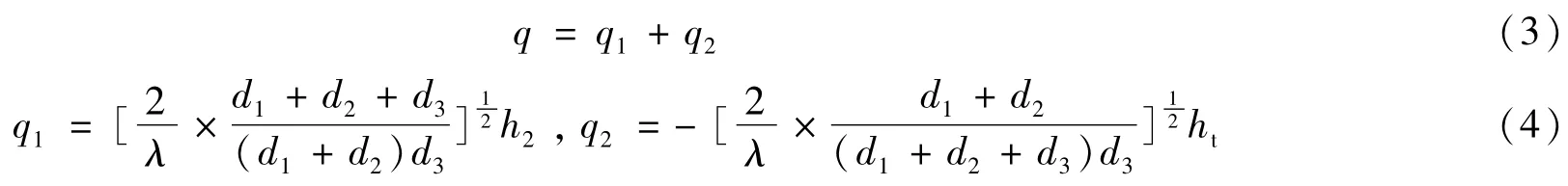
式中，λ為波長，d1、d2、d3分別為天線與第一個雷達柵、第一個雷達柵與第二個雷達柵、第二個雷達柵與目標間的距離。

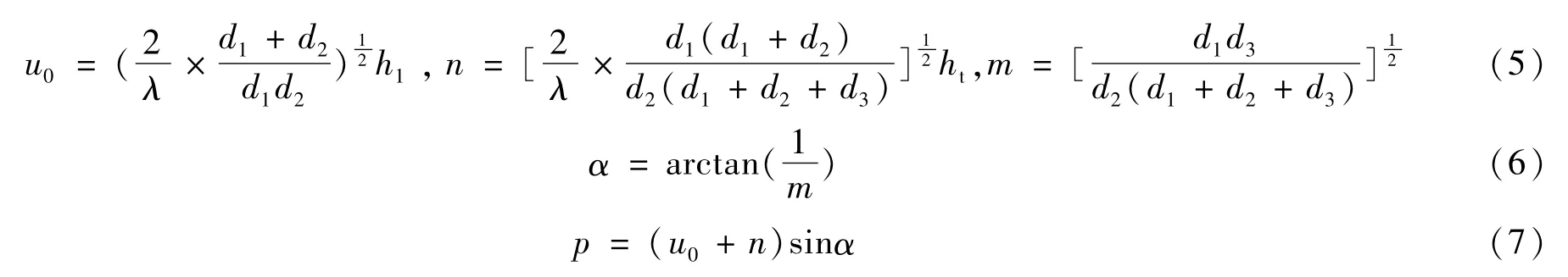
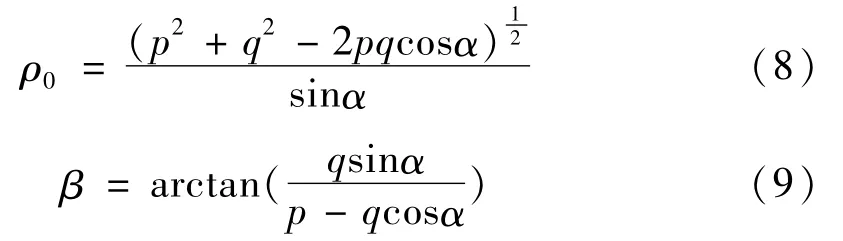
式(6)～(9)中，α、p、ρ0、q、β等參數的物理意義見圖1。

當p≥0、q＞0且式(1)中m前面的符號為負時，式(1)的積分區域如圖1中的陰影部分S1、S2所示。圖中，陰影部分的頂點為o′，oo′的長度為ρ0，γ1=β，γ2=π-αβ。oo′的延長線o′N將陰影區域分為兩個部分S1、S2(其它條件下的積分區域圖形見參考文獻［1］)。

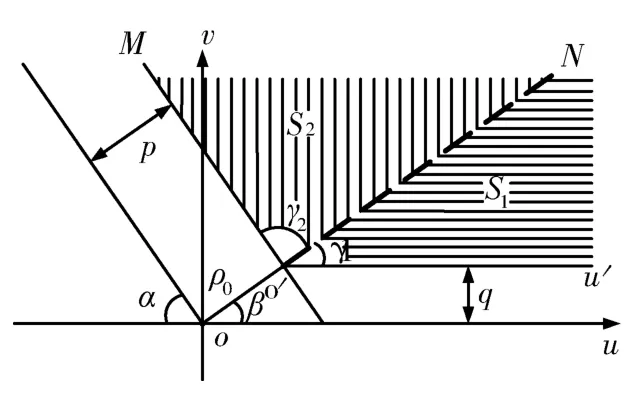
圖1 Fresnel面積分I-的積分區域示意圖(p≥0，q＞0)Fig.1 Schematic diagram of integral domain of Fresnel surface integral I-

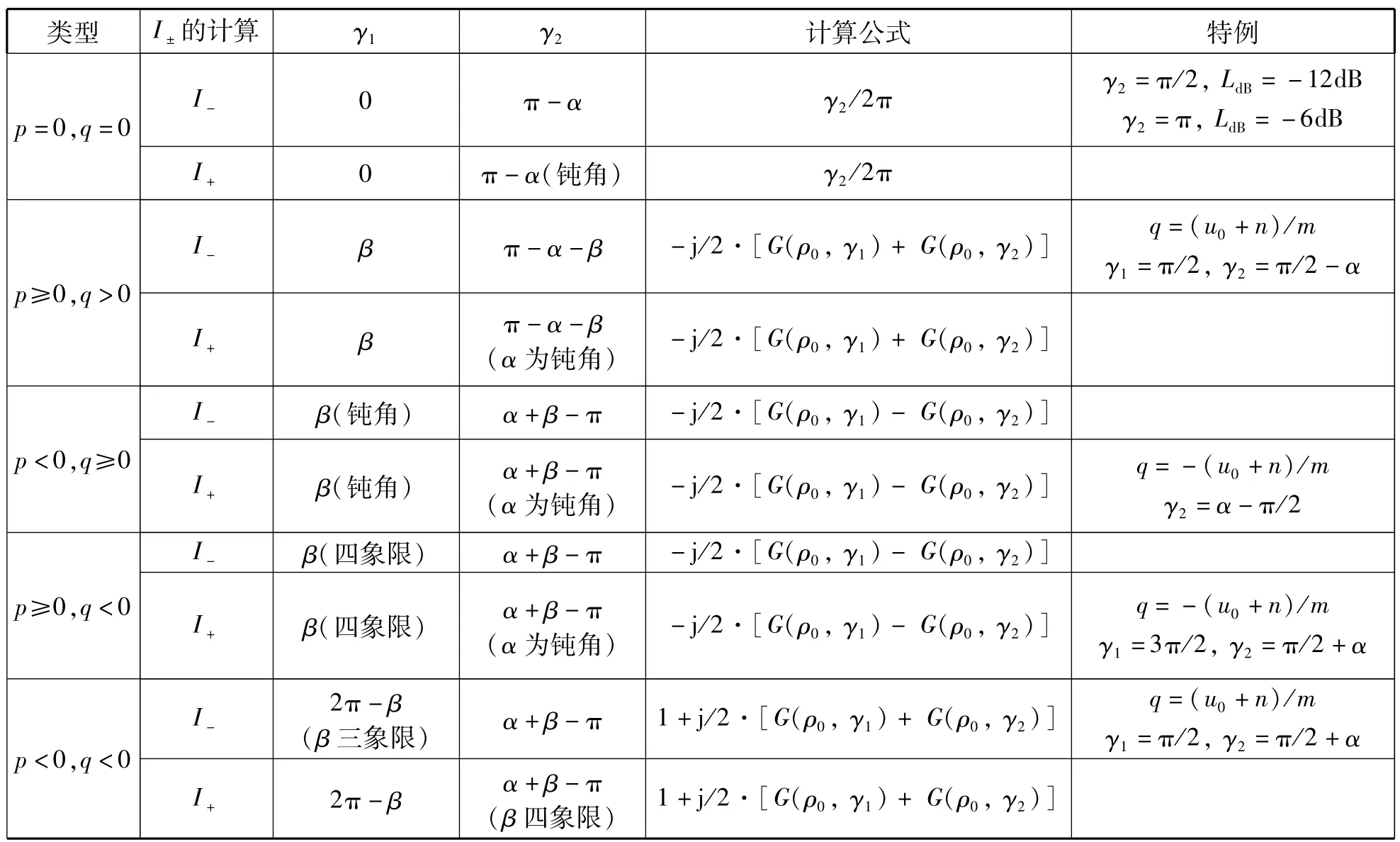
Table 1 Type of Fresnel surface integral表1 Fresnel面積分的類型［1］

2 G(ρ0，γ)的計算

Fresnel面積分的一般形式為

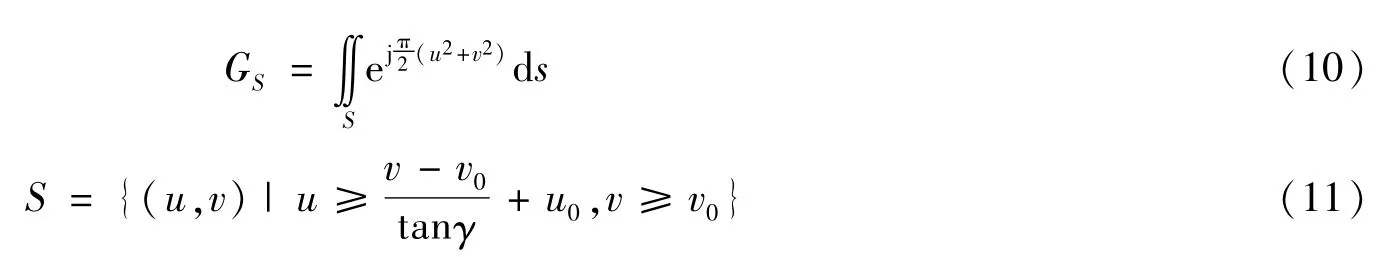
式(10)的積分區域見圖2。

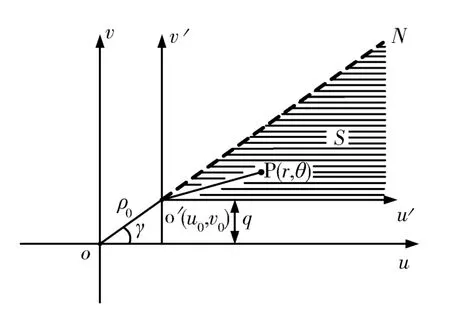
圖2 Fresnel面積分的積分區域示意圖Fig.2 Schematic diagram of integral domain of Fresnel surface integral

為便于計算，由

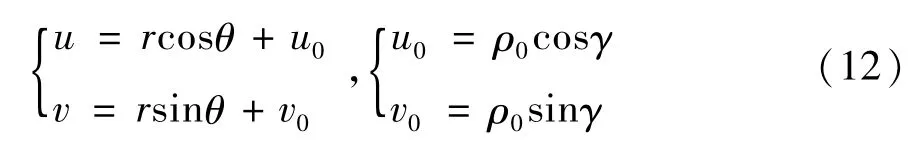
可得

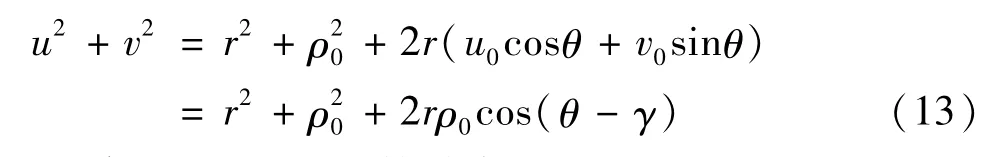
將式(13)代入式(10)，化簡并令

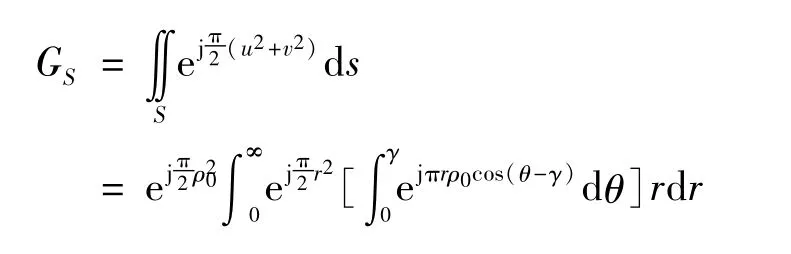
由雅可比-安格爾(Jacobi-Anger)恒等式有［7］

代入式(14)，得

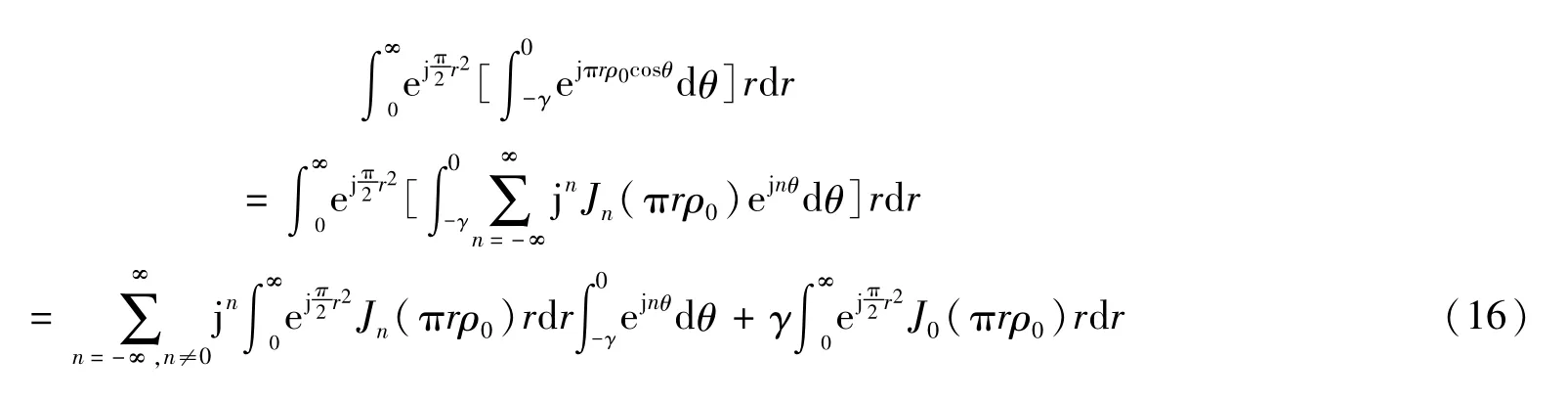
因

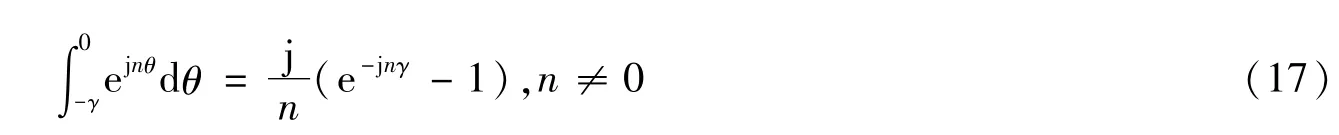
有

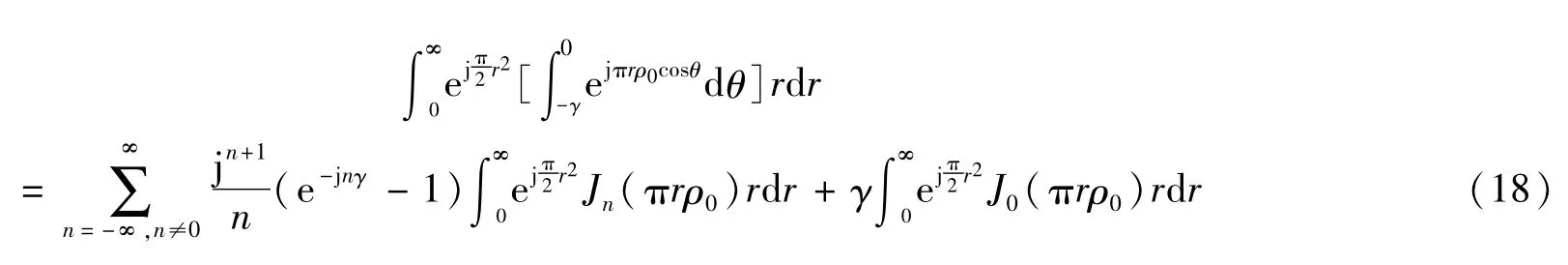
由Bessel函數的性質［7］

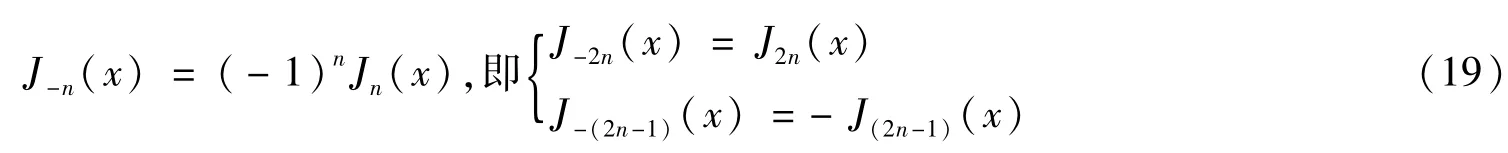
可將式(18)分解為下列五項之和

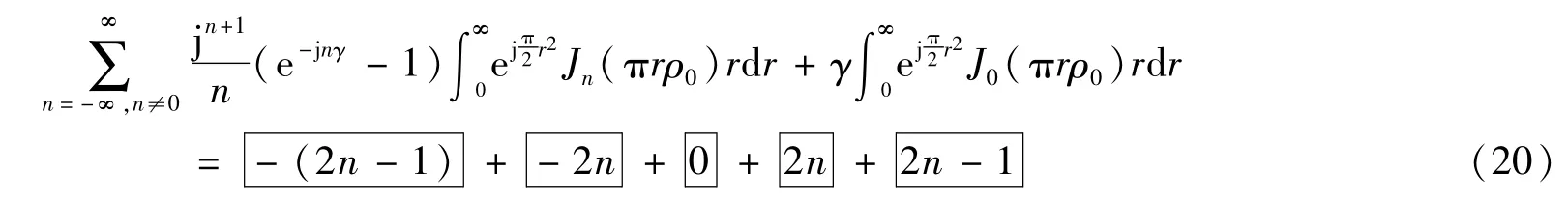
式中

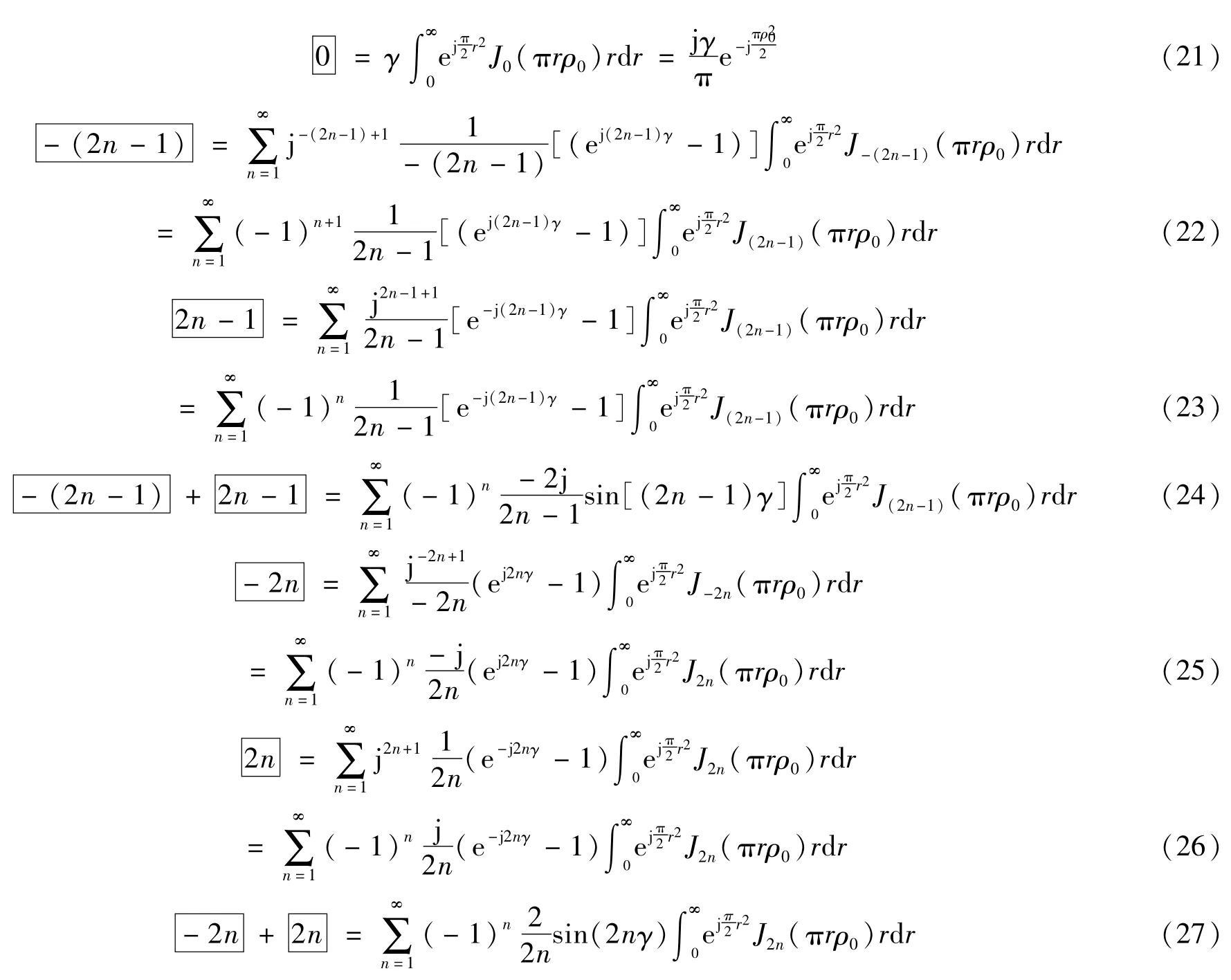
利用Bessel函數積分的關系式［7］

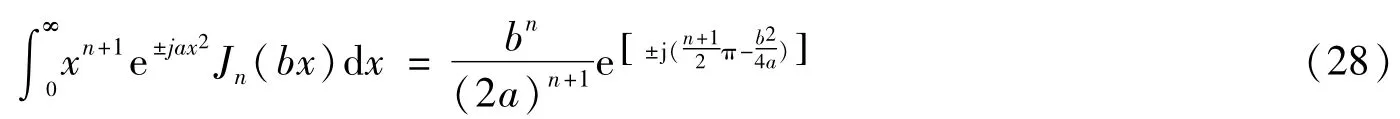
式中，a＞0，b＞0，1/2＞Ren＞-1(Re:實部)。

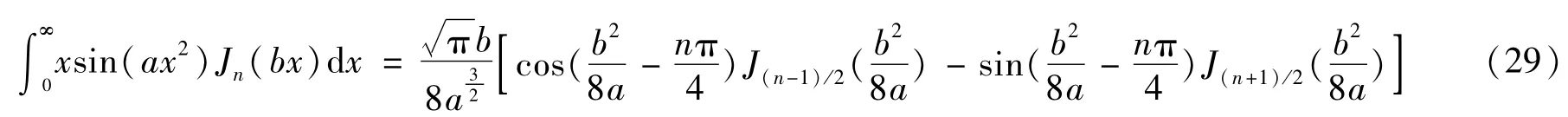
式中，a＞0，b＞0，Ren＞-4。

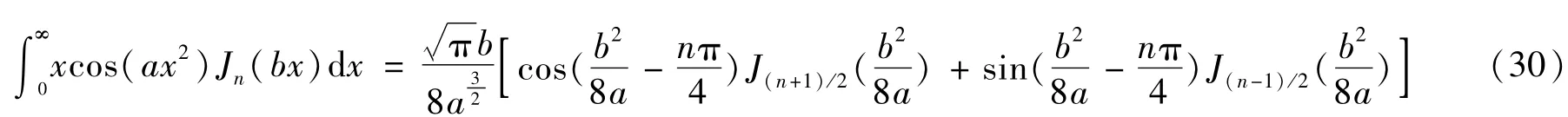
式中，a＞0，b＞0，Ren＞-2。

將式(24)、式(27)中積分項化簡為

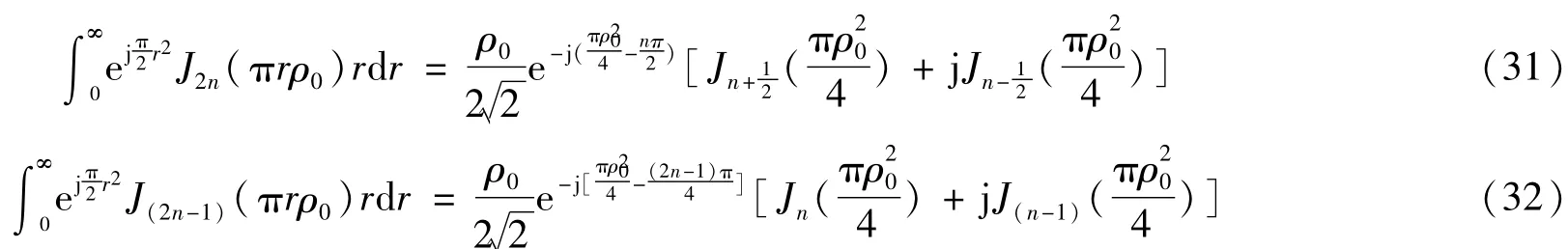
將式(20)代入式(14)，得

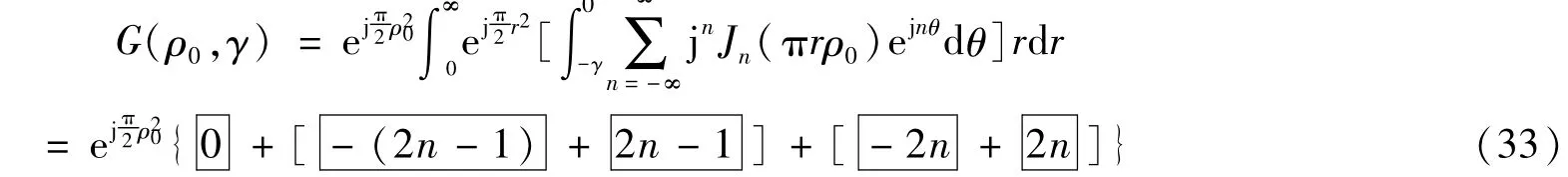
由式(21)、式(24)和式(27)可知

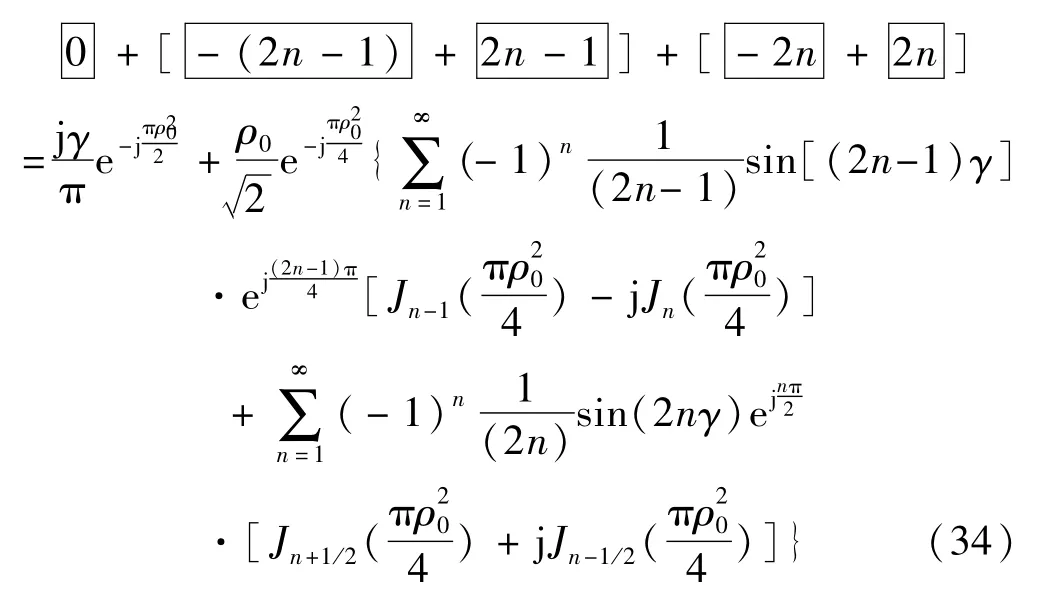
將上式代入式(33)，得

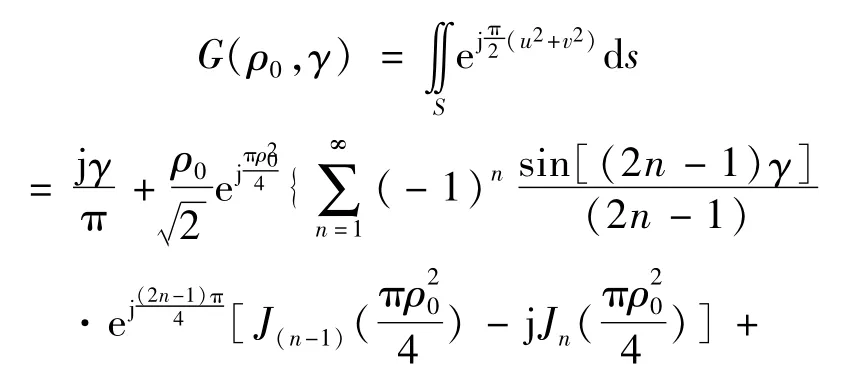
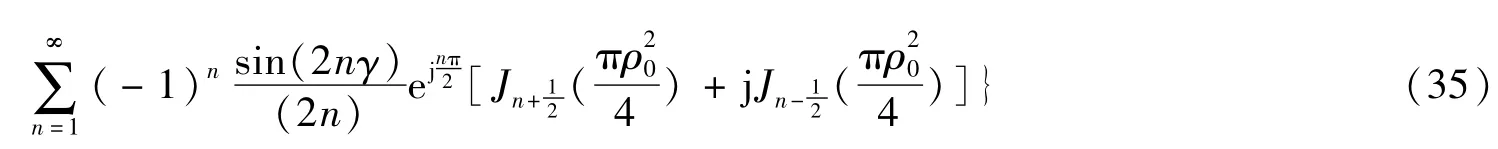
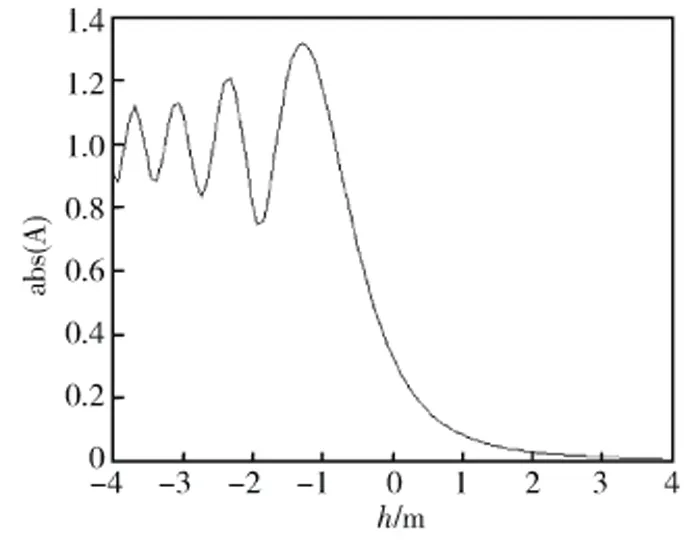
圖3 由本文計算方法得到的文獻［3］圖1算例的計算結果Fig.3 Calculation results of Literature 3 Fig.1 by the proposed method in this paper(f=1GHz，d1=d2=d3=10m，h=h1=h2=-4m～4m，hA=hT)

此即為本文所得的Fresnel面積分近似計算公式。

3 算例驗證

為驗證本文近似計算公式的有效性，利用式(35)分別計算文獻［3～5］給出的算例。圖3為由式(35)得到的文獻［3］圖1算例的計算結果(注:圖3中的縱坐標abs(A)為復衰減函數A的絕對值，A=E/EO，E為設置雷達柵時目標處的電場強度，EO為無雷達柵時目標處的電場強度，詳見文獻［3］)，圖4為由式(35)得到的文獻［5］圖4算例的計算結果，計算時式(35)中的n取1～100。表2給出了文獻［4］第8節算例的計算結果對比。由圖3、圖4可以明顯看出，利用本文的計算公式可得到與文獻［3，5］完全一致的結論。從表2可以看出:當n取1～50時，其結果已滿足計算精度要求。

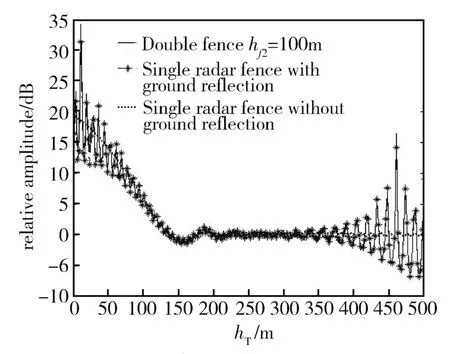
圖4 由本文計算方法得到的文獻［5］圖4算例的計算結果Fig.4 Calculation results of Literature 5 Fig.4 by the proposed method in this paper(VV-polarization，f=0.9GHz，d1=3000m，d2=2000m(Single Radar Fence，d2=5000m)，d3=3000m，h f1=h A=100m，h f2=0，Γ1=Γ2=Γ3=1)

表2 與文獻［4］計算結果的對比Table 2 Comparison of the calculation resultswith themethods in this paper and in Literature 4

4 結束語

本文針對傳統Fresnel面積分計算方法存在的參數(γ1、γ2、η等)分類、判斷多元，計算過程復雜、繁瑣等問題，提出了一種新的近似計算方法。仿真結果表明:與傳統計算方法相比，本文提出的近似計算方法物理意義清晰，計算方法簡單，計算量小且收斂速度快，為Fresnel面積分的相關工程應用提供了便利。

［1］趙雄文.計及反射的刃峰、尖劈、平頂障礙繞射場的一致性解法［D］.青島:中國電波傳播研究所碩士學位論文，1992.

［2］Schneider Michael， Luebbers R J.A General， Uniform Double Wedge Diffraction Coefficient［J］.IEEE Transactions on Antennas and Propagation，1991，39(1):8～14.

［3］Savov SV， Andersen JB.Efficient Method for Calculation of Fresnel Double Integral［J］.Electronics Letters， 1995， 31(6):435～437.

［4］Millington G， Hewitt R， Immirzi F S.The Fresnel Surface Integral［J］.IEE Proceedings， 1962， 109C(162):430 ～437.

［5］Zhao Xiongwen， Vainkainen Pertti.Multipath Propagation Study Combining Terrain Diffraction and Reflection［J］.IEEE Transactions on Antennas and Propagation，2001，49(8):1204～1209.

［6］張新好.0.8GHz-18GHz全頻段外場散射及天線測量技術研究［D］.北京:北京航空航天大學博士學位論文，2011:63～66.Zhang Xinhao.Study on the 0.8GHz-18GHz Outdoor RCS and Airborne Antenna Measurement System［D］.Beijing University of Aeronautics and Astronautics，2011:63～66(in Chinese).

［7］《數學手冊》編寫組.數學手冊［M］.北京:高等教育出版社，1979:628.

［8］Gradshteyn IS， Ryzhik IM.Tables of Integrals， Series and Products［M］.7th edition.New York:Academic Press， 2007:706，739.