二項分布下的MSPOT方法研究

王雪崢

(92493 部隊 98 分隊 葫蘆島 125000)

引 言

在裝備試驗鑒定中，經常會涉及到服從二項分布的指標參數，例如彈炮命中概率的鑒定問題、復雜系統可靠性鑒定問題等。關于二項分布參數的檢驗方法，常用的有經典假設檢驗［1］、貝葉斯假設檢驗［2］以及序貫檢驗［3］。不管是哪一種假設檢驗方法，都離不開統計假設。以導彈命中概率p(0＜p＜1)為例，給出命中概率指標為某一個數值p0和最低可接受值p1，則相應的簡單假設為:H0:p=p0，H1:p=p1。試驗方案應具有如下特性:當實際p≥p0時，應以不低于(1-α)的概率通過驗證試驗;當p≤p1時，應以不高于β的概率通過驗證試驗。α為生產方風險，β為使用方風險。在該假設條件下，不管是采用經典假設檢驗、貝葉斯假設檢驗，還是序貫檢驗，最終得出的結論是接受H0:p=p0，認為實際導彈命中概率p≥p0;或者拒絕H0:p=p0，而接受H1:p=p1，認為實際導彈命中概率p≤p1。當導彈實際命中概率p處在［p1，p0］區間上時，這種簡單假設方案無法做出判斷，只會判給p≥p0或p≤p1，這對于子樣數較少的導彈類武器試驗來說，無疑減少了試驗信息，甚至是提供了錯誤的試驗信息。本文提出的多假設序貫驗后加權檢驗MSPOT(Multi-hypothesis Sequential Posterior Odd Test)方法很好地解決了上述問題。

所謂多假設，是指統計假設打破傳統兩個假設(即原假設和備擇假設)的情況，根據實際需求，將參數空間劃分成多個，對應出現多個統計假設。例如前文導彈命中概率問題，參數空間劃分為0＜p＜p1，p1≤p＜p0，p0≤p＜1三個區域，則對應三個假設為H0:0＜p＜p1，H1:p1≤p＜p0，H2:p0≤p＜1。這里不再分原假設和備擇假設，而是根據具體參數空間的意義來判斷，比如H0為真時，說明0＜p＜p1，即命中概率沒有達到最低可接受值;當H1為真時，說明p1≤p＜p0，即命中概率達到最低可接受值，但尚未達到設計指標要求;當H2為真時，說明p0≤p＜1，即命中概率達到設計指標要求。

序貫驗后加權檢驗SPOT(Sequential Posterior Odd Test)方法通常是將A.Wald提出的序貫概率比檢驗SPRT(Sequential Probability Ratio Test)方法的似然比換作似然函數在Θ0、Θ1上的驗后加權比，Θ0、Θ1是原假設和備擇假設所對應的參數空間。SPOT方法是一種在現場試驗中根據試驗樣本的實際情況進行實時統計決策的試驗方法，這種方法一方面可以充分利用驗前信息，另一方面又可視試驗參數樣本的實際情況決定是否停止試驗新的樣本，它在工程上，特別是小子樣問題的解決上，具有重要的應用價值［4～6］。

MSPOT方法是在多假設序貫概率比檢驗MSPRT(Multi-hypothesis Sequential Probability Ratio Test)［7，8］方法基礎上，將多簡單假設推廣到更具一般性的多參數空間假設，即Θ0，Θ1，...，ΘM-1，M為假設的個數，Θi(i=0，...，M-1)可以是單點值，也可以是連續的參數空間。當為單點值時，便是MSPRT方法，即多簡單假設的MSPOT方法。當為連續的參數空間時，便是多復雜假設的MSPOT方法。可見，MSPRT方法是MSPOT方法的一種特例，MSPOT方法更具一般性。

圖1給出了MSPOT方法與MSPRT、SPRT、SPOT方法的關系。由圖可見其他幾種方法都是MSPOT方法的特例，MSPOT方法的優越性在于其既利用了驗前信息，又解決了多參數空間假設檢驗的問題，包括多簡單假設和多復雜假設，而MSPRT方法只考慮了多假設中的簡單假設問題，SPOT方法雖然包括簡單假設和連續參數空間假設，但只考慮了兩假設。由此可見，MSPRT、SPRT和SPOT都具有自身的局限性。

圖1 MSPOT方法與MSPRT、SPRT、SPOT方法的關系Fig.1 Relationship of the MSPOT，MSPRT，SPRT and SPOT methods

本文基于多簡單假設SPOT方法［9］和多參數空間復雜假設SPOT方法［10］，研究提出了MSPOT方法，并針對常見的成敗型參數試驗方案設計問題，具體推導了二項分布參數下MSPOT方法的計算公式，對解決成敗型參數檢驗問題具有一定的指導意義。

1 MSPOT方法

1.1 MSPOT方法的序貫決策過程

設X1，X2，…是獨立同分布隨機變量，概率密度為f。如果密度函數f的參數為θ，設有參數空間Θ，Θ=Θ0∪Θ1∪…∪ΘM-1，則多假設為

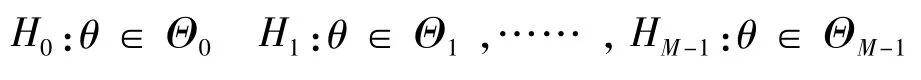
如果各參數空間為單點集，則假設為多簡單假設;如果參數空間為連續參數空間集，則假設為多復雜假設。

已知θ的先驗分布為π(θ)。根據MSPRT方法的思想［7］，真實假設具有相對較大的后驗概率，則有如下的序貫決策規則。

①序貫停止規則

序貫停止時的樣本數N取第一個大于0且使得對于至少一個k成立的n值。Ak為閾值，為后驗概率。

當假設為多簡單假設時有

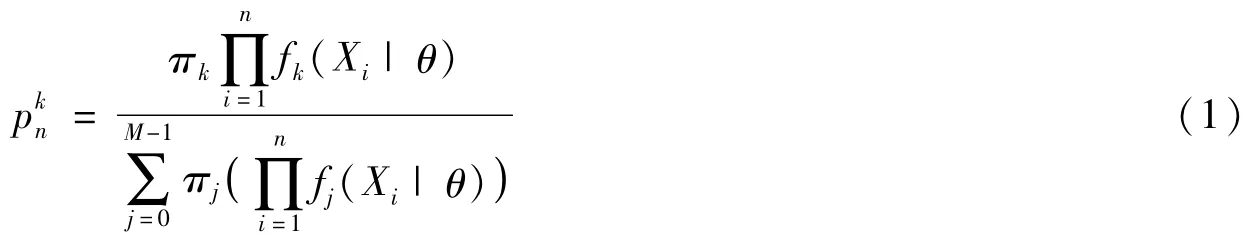
當假設為多復雜假設時有

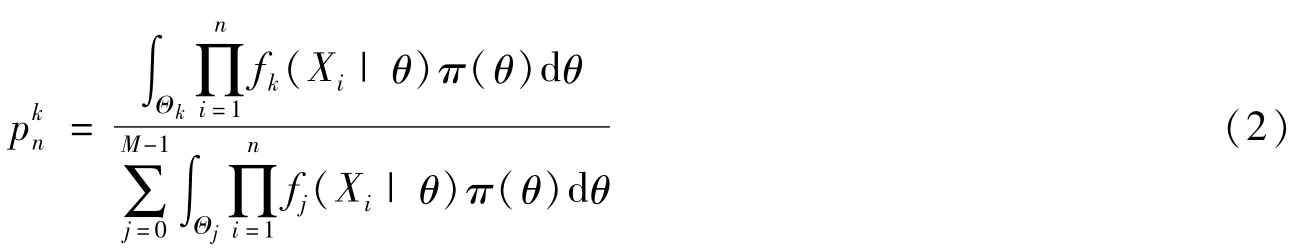
其中fk(X|θ)表示概率密度函數f在假設Hk成立參數空間為Θk時的概率密度形式。

②序貫決策規則

上述序貫決策規則中，公式形式比較復雜，因此，將式(1)、式(2)代入序貫停止規則不等式進行化簡整理。序貫決策過程轉化成:N取第一個大于0且使得Onk＜Ak至少對一個k成立的n值，如果Onk=min{Onj:j=0，···，M-1}，則Hk為真實假設。

當假設為多簡單假設時有

當假設為多復雜假設時有

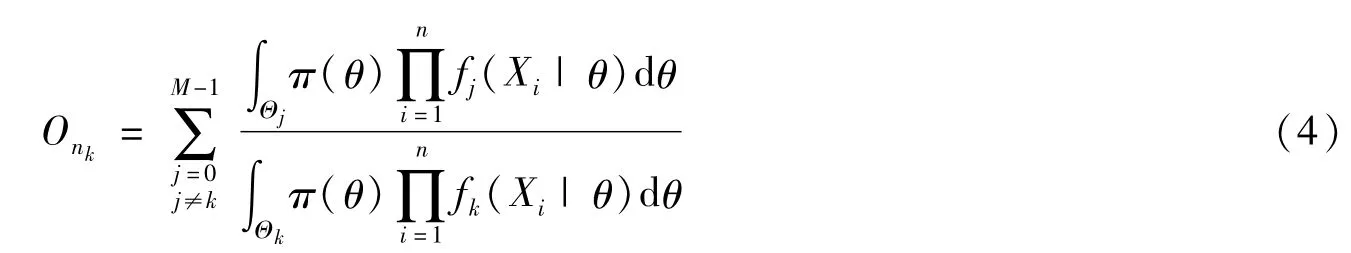
1.2 MSPOT方法中閾值Ak的計算過程

對于上節的序貫決策過程，當樣本分布已知、先驗概率密度已知時，Onk的計算容易得出。至于閾值Ak(k=0，1，…，M-1)的計算，雖然多簡單假設對應的MSPRT方法中有明確的數值表達式［7，8］，但計算起來很復雜，而多復雜假設的MSPOT方法中Ak的計算還很難找到確切的數值表達式。因此，本文采用仿真搜索法計算Ak。從序貫停止規則可以看出，Ak的大小直接影響停止時的樣本數，進而影響決策的準確度。經分析，Ak越小，相應的N越大，決策結果越準確。因此Ak值并不是唯一確定的，在不影響決策判斷的前提下，為了方便計算，這里不妨設Ak均相等，采用仿真搜索方法進行求解，搜索策略如下:

設搜索步長為ε，這里取ε=0.05。令初值Ak=A=1(k=0，1，…，M-1)，誤判率允許值α0=0.3。所謂誤判率是指Hk為真實假設時，決策判斷Hk為假的概率，這里用誤判的頻率代替誤判概率，即誤判的次數/序貫試驗總次數。

①產生分布密度為π(θ)的隨機參數值θi(i=1，2，…，N)，N是事先給定的，這里令N=10。

②生成服從f(Xi|θ)的隨機樣本Xi(i=1，2，…，n)，計算

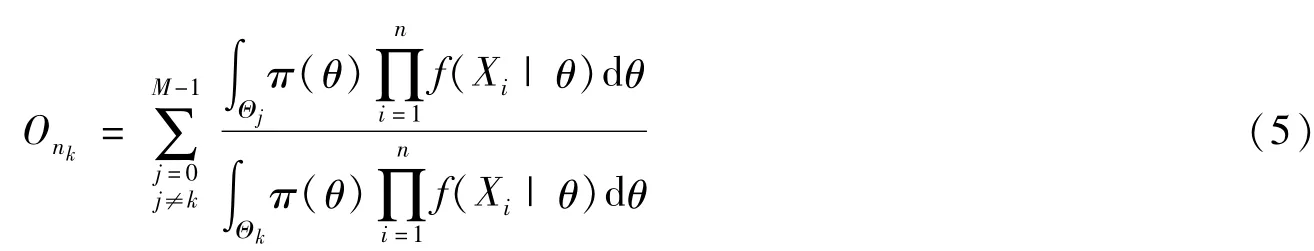
按照1.1節序貫決策過程進行序貫決策判斷。

③對步驟②操作重復進行K次，K是事先給定的，這里令K=100。計算出θi情況下序貫試驗的誤判率

④計算平均誤判率

通過上述過程便可求出待檢驗樣本的閾值A，即Ak(k=0，1，…，M-1)。

1.3 MSPOT方法截尾序貫決策過程

給定試驗樣本數N，當根據1.1節的序貫決策過程無法停止試驗時，強制停止試驗。截尾序貫決策規則為:如果則Hk為真實假設，其中ONj的計算公式同式(3)、式(4)。

2 二項分布參數檢驗的MSPOT方法

假設參數p的最低可接受值為p1，指標值為p0，則對應的多復雜假設為

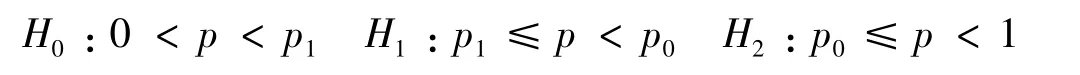
其參數空間為

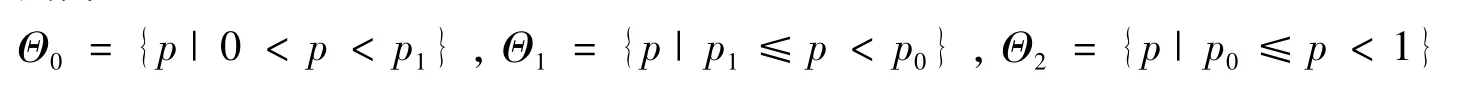
根據式(4)計算得到多復雜假設情況下

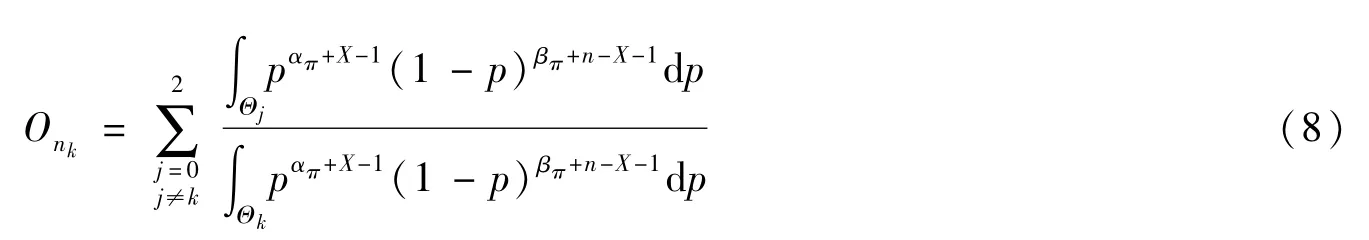
若采用多簡單假設，則可用參數區間中點代表參數空間，即取

對應的多簡單假設為

H0:p=μ0H1:p=μ1H2:p=μ2

根據式(3)計算得到多簡單假設情況下

當參數p無先驗信息時，各假設的先驗概率相同，則

3 仿真算例及分析

在導彈試驗過程中，對導彈的命中概率進行檢驗。當導彈在規定區域爆炸，認為導彈命中目標，記為1;否則認為失敗，記為0。可見，導彈的命中概率試驗是一個獨立的n重伯努利試驗，因此在n次試驗中導彈命中目標的次數X服從二項分布，即X～b(n，p)。假設某型導彈命中概率p1=0.75為最低可接受值，設計指標p0=0.9，且沒有任何驗前信息。當p＜p1時，認為該指標沒有達到最低可接受值;當p1≤p＜p0時，認為該指標在最低可接受值和設計指標之間;當p≥p0時，認為該指標達到設計指標要求。由于沒有先驗信息可以利用，采用無驗前信息的多簡單假設MSPOT方法。給定允許誤判率α0=0.3，根據式(9)計算出μ0、μ1、μ2值，再根據1.2節步驟①～⑤計算出A=0.7，此時的平均誤判率α*=0.279。下面借助計算機模擬，應用MSPOT方法進行導彈命中概率仿真模擬試驗。Matlab［12］仿真模擬流程如圖2所示。

分別在三個參數空間取出一個值作為指標真值代表，例如取p=0.5＜p1，按照圖2流程進行序貫仿真試驗，所得結果如表1所示。當n=3時，有O30=0.1887＜A，停止試驗，此時O30=min{O30，O31，O32} ，判斷假設H0為真，這與p=0.5＜p1相符。p=0.8和p=0.95的仿真結果同樣證明了本文方法的正確性和有效性。

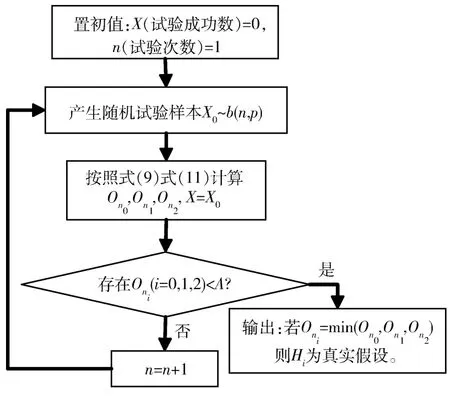
圖2 一次MSPOT試驗(p給定)模擬計算流程Fig.2 Flow chart of a MSPOT test calculation with given p

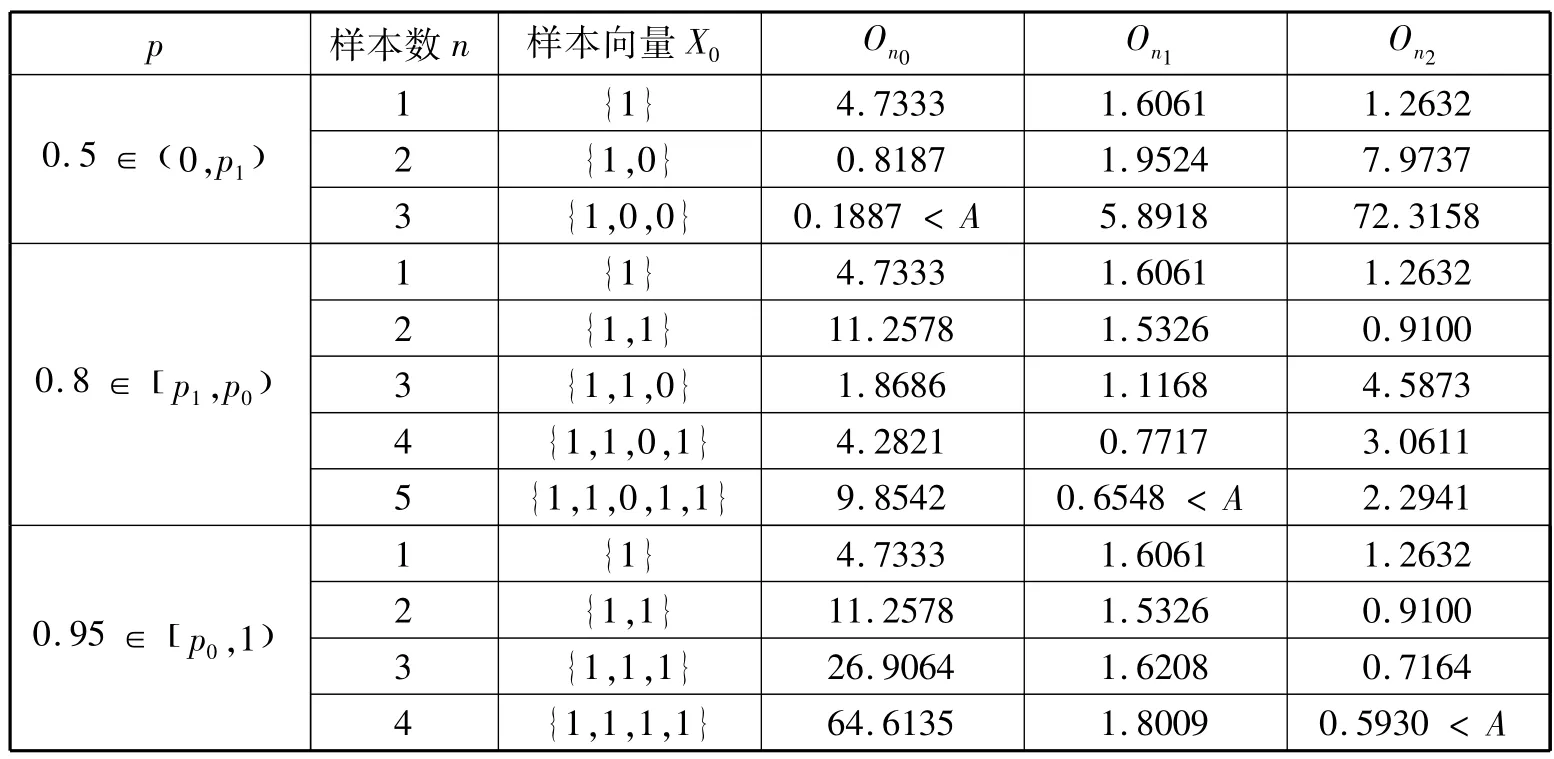
表1 多簡單假設MSPOT方法仿真試驗結果Table 1 The result of MSPOTmethod with multiple simple hypothesis

若事先已規定試驗次數，則采用截尾的MSPOT方法。例如，試驗次數為7次，如果有5次命中目標，記為(7，5)，則7次試驗中可能出現的試驗結果見表2。

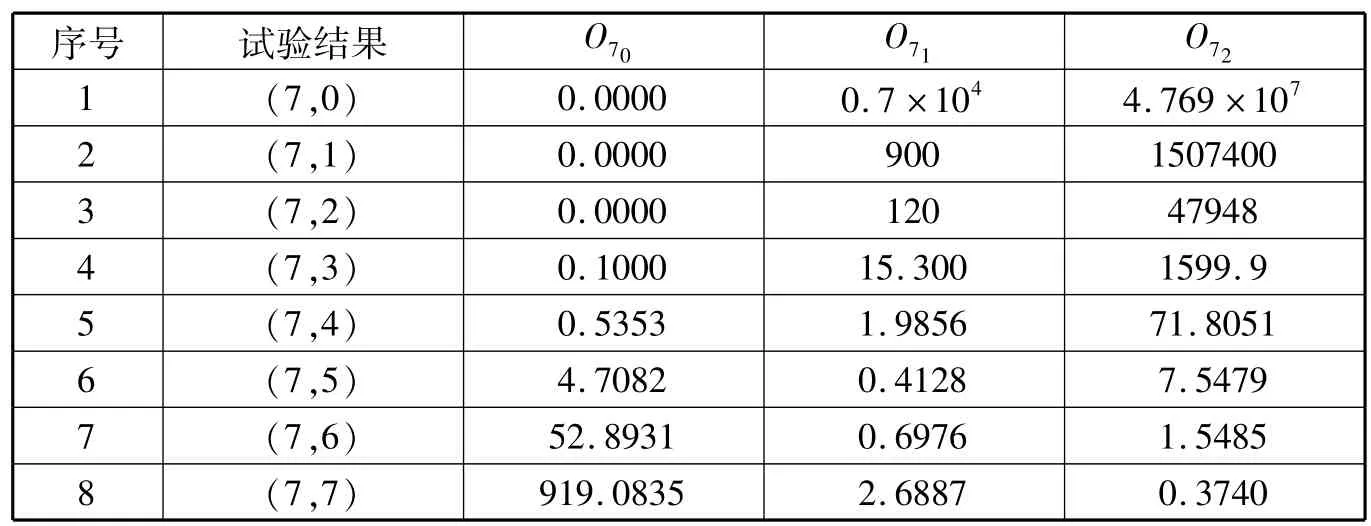
表2 試驗結果Table 2 Test results

從表2中可以看出，前五種試驗結果，根據截尾的MSPOT方法判斷O70最小，H0是真實假設，說明參數p滿足p＜0.75;試驗結果為(7，5)和(7，6)時，判斷O71最小，H1為真實假設，說明參數p滿足0.75≤p＜0.9;試驗結果為(7，7)時，判斷O72最小，H2為真實假設，說明參數p滿足p≥0.9。

4 結束語

從本文的計算結果可以看出，應用MSPOT方法進行試驗，試驗結果并不是簡單拒絕或接受，而是能夠提供試驗參數所在的區間。它有效解決了傳統簡單假設中，最低可接受值和設計指標值之間的模糊參數區域問題，為試驗雙方提供更多的試驗信息。本文例子沒有驗前信息，如果在實際試驗中能夠得到相對準確的驗前信息，則應用MSPOT方法進行試驗，結果將會更貼近實際。

［1］閆章更，濮曉龍.現代軍事抽樣檢驗方法及應用［M］.北京:國防工業出版社，2008.

［2］武小悅，劉 琦.裝備試驗與評價［M］.北京:國防工業出版社，2008.

［3］楊萬軍，張士峰，蔡 洪.序貫檢驗方案分析——二項分布情形［J］.飛行器測控學報，2002，21(2):61～63.

［4］王國玉，申緒澗，汪連棟，等.電子系統小子樣試驗理論方法［M］.北京:國防工業出版社，2003.

［5］張金槐，唐雪梅.Bayes方法(修訂版)［M］.長沙:國防科技大學出版社，1993.

［6］陳孝強，武小悅.Bayes序貫驗后加權檢驗方法的仿真分析［J］.戰術導彈技術，2004，9(5):60～62.Chen Xiaoqiang， Wu Xiaoyue.Simulation Analysis of Sequential Posterior Odd Test Methods［J］.Tactical Missile Technology 2004，9(5):60～62.

［7］Baum W， Vecravalli V.A Sequential Procedure for Multihypothesis Testing［J］.IEEE Transactions on Information Theory，1994，40(6).

［8］Woodroof M.Nonlinear Renewal Theory in Sequential Analysis［M］.SLAM，1982.

［9］王雪崢，武小悅.多簡單假設的SPOT方法［J］.系統工程與電子技術，2007，29(9):1581～1584.Wang Xuezheng， Wu Xiaoyue.Multi-simple-hypothesis SPOT Method［J］.Systems Engineering and Electronics， 2007，29(9):1581～1584.

［10］王雪崢，韓成哲.可靠性試驗中多參數空間復雜假設的SPOT方法研究［J］.戰術導彈技術，2010，(1):48～52.Wang Xuezheng，Han Chengzhe.Development of SPOT Method for Multiple Parameter Spaces with Complex Hypothesis in Reliability Test［J］.Tactical Missile Technology， 2010， (1):48 ～52.

［11］曲寶忠，孫曉峰.海軍戰術導彈試驗與鑒定［M］.北京:國防工業出版社，2005.

［12］張志涌，等.精通MATLAB 6.5版［M］.北京:北京航空航天大學出版社，2003.