最優控制在吊車數控系統中的應用

張麗，朱珠

(1．江蘇鹽城工業職業技術學院機電工程學院，江蘇鹽城 224000;2．貴州理工學院電氣工程學院，貴州貴陽 550001)

0 前言

隨著現代生產力水平的提高，橋式起重機作為重要的搬運工具在工業生產中起到越來越重要的作用，并被廣泛應用于工廠、水電站、碼頭以及倉庫等各個領域［1］。然而，起重機在作業過程中極易引起吊重的擺動，并進一步引發安全事故。因此，為了提高橋式起重機的安全性與可靠性，提高生產效率，采用某些控制方法對其吊重擺動進行有效抑制是非常必要的［2-3］。但是，一些傳統的控制方法，如極點配置方法［4-5］等，很難使起重機控制系統的性能滿足現場環境的需求，因此有必要開展吊車系統控制技術的研究。

同時，目前的大多數研究中均針對連續吊車系統進行控制策略的研究［2-5］，一些復雜的連續域控制算法很難通過搭建模擬電路的方式實現，而工程應用時將其進行簡單的離散化處理并不可行。然而，隨著單片機和DSP的出現和發展，使得吊車系統的模塊化和全數字化更容易實現，控制算法的實現經常利用數字計算機，因此很有必要在離散領域研究吊車系統控制技術。這就要求我們在離散域內研究吊車控制系統的被控對象以及相應的控制算法，這也是文中的主要出發點。

LQR(Linear Quadratic Regulator)即線性二次型調節器［6］，其對象是現代控制理論中以狀態空間形式給出的線性系統，而目標函數為系統狀態和控制輸入的二次型函數。LQR最優設計是指設計出的狀態反饋控制器要使二次型目標函數最小化，故具備良好的綜合性能優勢。LQR理論是現代控制理論中發展最早也最為成熟的一種狀態空間設計法，特別可貴地，LQR可得到狀態線性反饋的最優控制規律，易于構成閉環最優控制，因此得到了廣泛的研究和應用［7-11］。此外，Matlab軟件的應用為LQR理論仿真提供了條件，更為實現穩、準、快的控制目標提供了方便。正是因為LQR這些優良的控制特性和品質，因此文中將其引入到吊車數控系統的設計中。

本文作者首先利用Lagrange方程建立了吊車系統的非線性數學模型。然后對所建立的連續數學模型進行離散化處理，并基于此，應用離散LQR最優控制理論研究起重機的吊重擺動控制策略。最后通過計算機仿真驗證文中控制方案相比傳統控制方案的性能優勢。

1 問題描述

吊車系統的整套機械部件安裝在一塊底板上，底板上固定著導軌、皮帶輪、電機、測速機、車位置反饋電位計，底板開槽，使吊擺垂下去。吊車組件包圍在軌道外，4個車輪在導軌上方運動、吊車板下面連著小車板支架和角位置電位計支架，兩支架之間安裝吊擺，在角位置電位計支架上裝有測量吊擺角度的單圈電位計。橋式吊車控制系統的示意圖如圖1所示。

圖1 橋式吊車控制系統示意圖

圖1中，M為車重，m為吊物質量，g為重力加速度，l為擺長，φ為擺角，u為伺服控制器的輸出電壓，x為車質心的水平位置，y表示吊物的水平位置，z表示吊物的豎直位置。

為了更加清楚地掌握單擺的運動模型，圖2給出其受力分析示意圖。

圖2 單擺的受力分析圖

圖2中，F表示吊車的控制力，T表示貨物受到的拉力。

單擺是一個兩自由度系統，廣義坐標為q1=x，q2=φ。系統的Lagrange函數為:

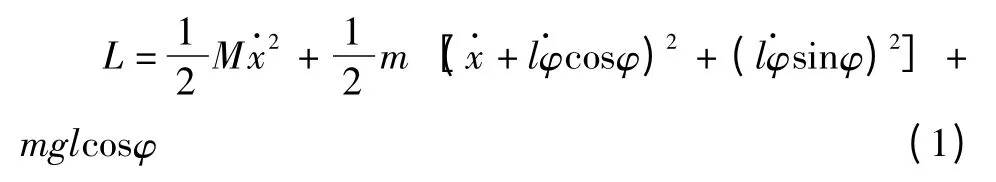
進一步可以得到:

根據式(2)，可以得到Lagrange方程組為:)

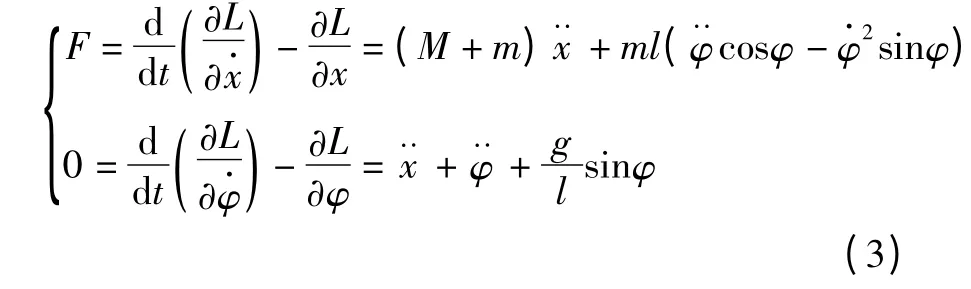
選取狀態變量為xp=［xφ］T，則Lagrange方程組可變形為如下狀態空間的形式:

其中，

式(4)中的控制力F是由直流伺服電機提供的，并且通過精確控制直流電機可以得到期望的控制力。在忽略了感抗的影響以及啟動死區電壓后，可以將直流電機視為一個二階的線性系統，其模型如圖3所示。

圖3 直流電機的結構框圖

圖3中，Ra為電機的電樞電阻，Ke為電機的反電勢系數，Kt為電機的力矩系數，J為電機電樞繞組的轉動慣量，r為皮帶輪的半徑，ua為輸入到電機的控制電壓，Ⅰa為電樞電流，ω為電機的旋轉角速度。

根據圖3，可得到如下的傳遞方程:

將上式寫為關于時間的微分方程形式:

進一步整理可以得到:

同時，考慮到功率放大器的作用，則可以得到伺服電機的輸入電壓ua與控制器輸出電壓u之間的關系:

將式(7)—(8)代入到式(4)中，可以得到平衡位置附近處電機加單擺對象的數學模型:

其中，

至此，吊車系統的連續狀態空間方程建立完畢。于是，下一步吊車系統的控制目標是:當滑車在導軌上以一定速度和加速度運動時，應保持單擺的擺動角度最小，或單擺有任一初始擺角時，系統將使其迅速返回平衡位置。

2 離散控制方案設計

2．1 連續系統離散化

計算機控制系統與模擬控制系統的不同之處在于，在模擬系統中，信號的傳送不需要數字化;而計算機系統必須先進行A/D轉換，輸出控制信號也必須進行D/A轉換，然后才能驅動執行機構，吊車計算機控制系統的結構框圖如圖4所示。因為計算機有較強的計算能力，所以控制算法的實現和改變都很方便。

圖4 吊車計算機控制系統的結構框圖

由于實際的計算機控制是離散的，所以要將式(9)表示的系統離散化。若T為系統的采樣周期，則可根據［19］:

得到離散化后的系統為:

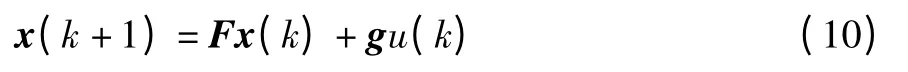
因為文中研究的吊車控制系統階數較高，如果直接通過轉換關系式(9)獲得離散系統的狀態矩陣F和控制向量u是很復雜的，因此我們可以借助具有強大計算功能的Matlab軟件，并進一步通過函數c2d實現，其具體實現形式如下:

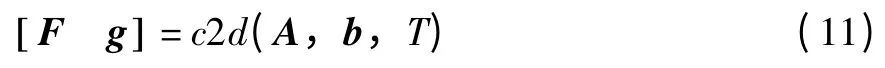
于是，下面將針對離散模型式(10)來設計吊車系統伺服電機的控制策略，該模型更符合數字控制系統的特性，具有較好的實用和工程應用價值。

2．2 離散最優LQR控制

針對2．1節建立的離散模型式(10)以及系統的控制目標，將利用最優二次型調節理論，設計吊車計算機系統的離散最優LQR控制器。

綜合考慮單擺狀態的收斂性以及電機的能量消耗，可以選取離散性能指標函數為:

不失一般性，Q選取為正定對稱陣，且R為正數。

假設吊車數字系統式(10)是可控的，為了實現性能指標函數式(12)的最優化，根據LQR最優控制理論，可以設計如下的離散控制律:

其中，k*表示最優控制增益向量，而且矩陣P滿足黎卡提矩陣代數方程:

同樣地，因為吊車數控系統的階數較高，若通過求解方程式(14)來獲取控制增益向量是不現實的。于是，我們仍然可以借助于Matlab計算功能，并采用函數care求取黎卡提矩陣代數方程(14)或采用函數lqr直接獲得控制增益向量k*，后者的具體實現形式為:

至此，關于吊車數字系統控制器的設計完畢，下面將通過計算機仿真來驗證其合理性。

3 仿真結果

仿真中，吊車系統的參數如表1所示。

表1 吊車系統的相關參數

注意，仿真時兩個不能直測得的狀態量(車的速度、擺的角速度)可以采用位移量或角度量差分計算。設擺角的初始角度為60°，小車的位移為-0．3 m。而且，直流力矩電機的最大控制電壓為25 V，其死區電壓為2 V。

將吊車系統參數值代入到狀態空間方程式(9)中，可得到系統矩陣和控制向量分別為:

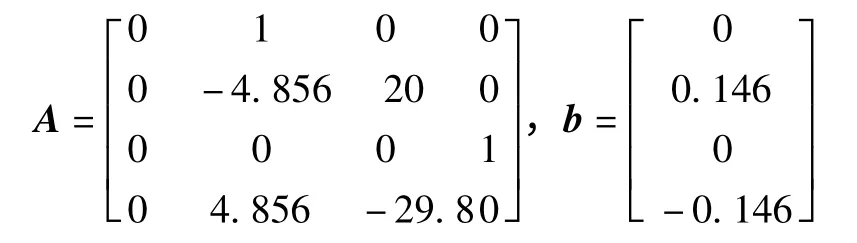
數控系統的采樣周期選取為0．025 s，則根據式(11)可以得到離散化之后系統矩陣和控制向量分別為:

根據可控性矩陣ctrl(F，g)的秩等于4，可以得到離散系統式(10)是完全可控的，因此我們可以通過狀態反饋實現系統極點的任意配置。

對于傳統的極點配置方法:設連續域內期望的極點分別為p1，2=-1，p3，4=-2±j2，則其對應的離散域內極點為q1，2=0．975，q3，4=0．95±0．047 5j。利用Matlab的acker函數，可求得反饋增益向量為:

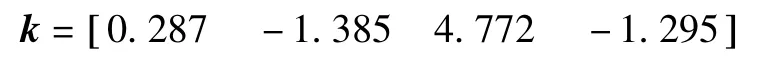
此時，給出極點配置方法下吊車系統各狀態的收斂曲線，如圖5所示。

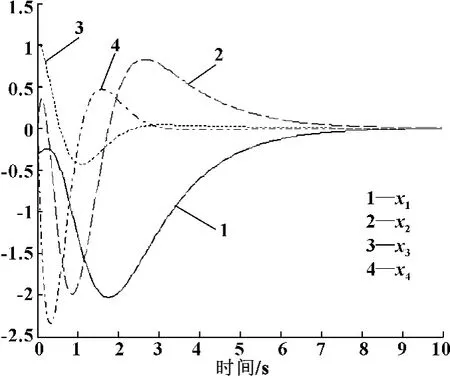
圖5 極點配置方法下吊車系統的狀態收斂曲線

對于離散LQR方法，首先選取二次型指標加權量為:

這時根據式(13)可以得到最優狀態反饋增益向量為:

此時，吊車系統的各狀態收斂曲線如圖6所示。

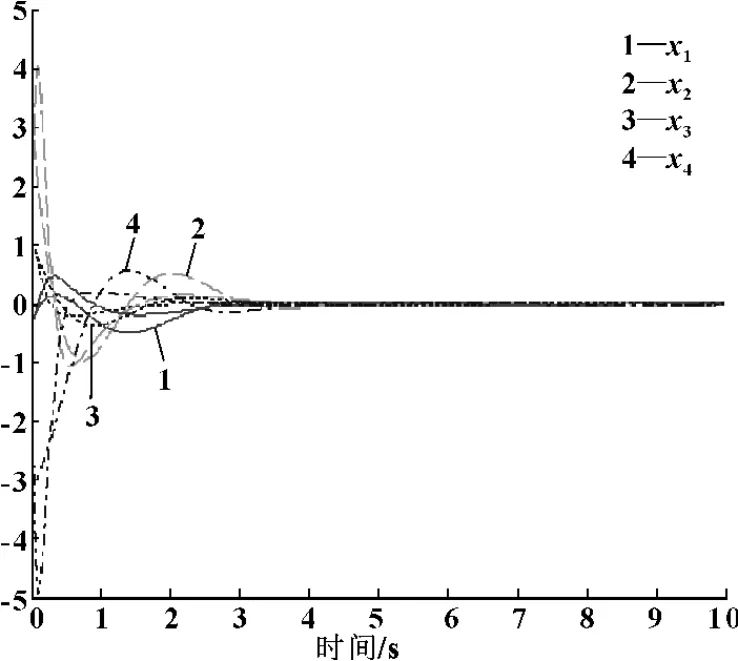
圖6 離散LQR下吊車系統的狀態收斂曲線(仿真1)

通過圖5和圖6可以看出，相比傳統的極點配置方法，離散LQR方法下吊車系統各狀態的收斂速度更快，從而體現了其控制優勢。

為了進一步了解Q和R對于吊車控制系統的影響，下面將分別調節兩個加權參數，并對比吊車系統的狀態收斂曲線。首先，在原來的基礎上，將Q陣修改為:

此時，吊車系統的各狀態收斂曲線如圖7所示。

圖7 離散LQR下吊車系統的狀態收斂曲線(仿真2)

根據圖6和圖7，可以看出，增大Q陣中的元素值后，小車速度和擺角角速度的超調量減小，說明相應的控制作用增強。

然后，在原來的基礎上，修改R的值為100，這時吊車系統的各狀態收斂曲線如圖8所示。

圖8 離散LQR下吊車系統的狀態收斂曲線(仿真3)

根據圖6和圖8可以看出，增大R的值后，系統的調節時間延長，控制作用減小。因此，可以從實際的性能需求調節狀態誤差加權矩陣Q和控制量加權系數R的值。

4 結論

最優LQR理論在控制系統的設計中應用方便，求解簡單，因此將其應用于吊車數字系統的控制中。仿真結果可以看出，相比傳統的極點配置方法，離散LQR方法可保證吊車數控系統更優越的收斂性能。而且，離散LQR方法的調試過程較為簡單，易于工程實現。但是，如果加權矩陣Q和加權系數R選擇不合理，設計出來的控制系統是不滿意的，此時所謂的“最優”只是使指標的最小化。通常把Q陣中的加權系數增大，則對應的狀態變量會收斂的更快些，把系數R增大則對應的控制量會減小些。

［1］高丙團，陳宏鈞，張曉華．龍門吊車系統的動力學建模［J］．計算機仿真，2006，23(2):50-53．

［2］李樹江，胡韶華，吳海．基于LQR和變論域模糊控制的吊車防擺控制［J］．控制與決策，2006，21(3):289-292．

［3］楊斌，劉惠康，代文蕤．橋式起重機防擺控制器的設計［J］．制造業自動化，2012，34(1):122-124，131．

［4］賈諾，王輝．吊車系統的狀態反饋控制的極點配置法［J］．哈爾濱師范大學:自然科學學報，2004，20(4):10-15．

［5］袁浩，徐真真，王先來．極點配置方法在起重機機架模型中的應用［J］．實驗室研究與探索，2006，25(12):20-24．

［6］NAIDU D S．Optimal Control Systems［M］．FL，USA:Crc Press，2002:101-149．

［7］SHAKIR H，KIM WJ．Nanoscale Path Planning and Motion Control with Maglev Positioners［J］．IEEE/ASME Trans．Mechatronics，2006，11(5):625-633．

［8］BASINA M，RODRIGUEZ-GONZALEZA J，FRIDMANB L．Optimal and Robust Control for Linear State-delay Systems［J］．Journal of the Franklin Institute，2007，344(6):830-845．

［9］DRAGAN V，MUKAIDANI H，SHI P．The Linear Quadratic Regulator Problem for a Class of Controlled Systems Modeled by Singularly Perturbed ito Differential Equations［J］．SIAM Journal on Control and Optimization，2012，50(1):448-470．

［10］藍會立，高遠，譚光興，等．車輛懸架LQR控制器權值優化方法［J］．科學技術與工程，2013，13(17):75-77．

［11］劉曉培．基于遺傳算法的汽車主動懸架LQR控制器的優化設計［J］．組合機床與自動化加工技術，2013(6):78-80．