福建省2015年三角函數解法探究
吳明庭
(福建石獅石光中學)
三角函數歷來都是高中數學的重要組成部分,是高考中的重點和難點,同時也是必考內容,三角函數在考試中的比重和分值較大。函數的求值問題實質就是三角轉換的基礎內容,通常包括三種類型:非特殊三角函數式求值、解三角形求值以及位置角的三角函數式求值。對于這類問題的解答,需要熟練掌握三角函數的基本公式以及變換形式,與此同時,還會運用到相應的技巧與方法,才可以簡潔、迅速又準確地對式子化簡求值。2015 年福建省高考試卷中就包含典型的三角函數試題,本文摘取了其中的試題,通過這幾道題的解法,來探究和感悟三角函數的求值方法。
一、考試原題:2015 年高考福建卷理科第II 卷,第19 題
已知函數f(x)的圖像是由函數g(x)=cosx 的圖像經如下變換得到:先將g(x)圖像上所有點的縱坐標伸長到原來的2 倍(橫坐標不變),再將所得到的圖像向右平移個單位長度.
(Ⅰ)求函數f(x)的解析式,并求其圖像的對稱軸方程;
(Ⅱ)已知關于x 的方程f(x)+g(x)=m 在[0,2p)內有兩個不同的解a,b.
(1)求實數m 的取值范圍。
(一)點評
此題主要通過考查學生對三角函數中圖像與性質、三角恒等式轉換等基礎知識,重點測試了學生綜合解題能力,包括運算求解能力、抽象概括能力、推理論證能力等多種能力,同時還考查了學生函數與方程思想、分類與整體思想、轉化與規劃思想、數形結合運用能力等多種綜合學習能力及思想。
(二)試題解析
(Ⅰ)縱向伸縮或平移:g(x)→kg(x)或g(x)→g(x)+k;
橫向伸縮或平移:g(x)→g(ωx)(縱坐標不變,橫坐標變為原來的倍),g(x)→g(x+a)(a>0 時,向左平移a 個單位;a<0 時,向右平移a 個單位);
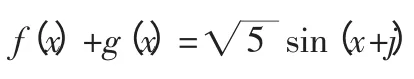
解法一:
(Ⅰ)將g(x)=cosx 圖像上所有點y 軸坐標伸長到原來的2倍,x 軸坐標不變;
于是,得到y=2cosx 圖像,然后將y=2cosx 的圖像向右平移個單位長度;
(1)(fx)+g(x)=2sinx+cosx
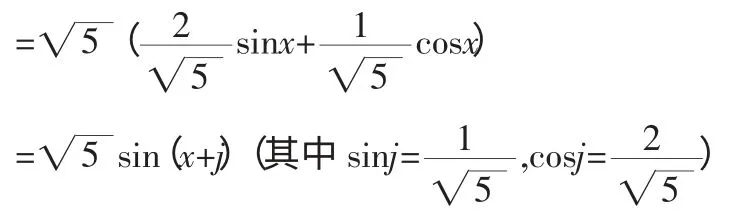
解法二:
(1)參照解法一
(2)①參照解法一
所以cos(a+j)=-cos(b+j)
于是:
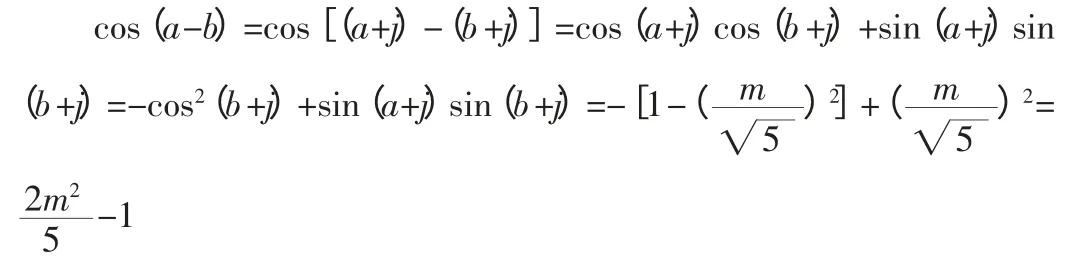
此方法重點考查的是三角函數圖象性質及其變化公式,同時考查了輔助角公式以及誘導公式。通過證明對比,不難看出,福建高考數學試題具有明顯的開放性,問題的答案也不是唯一的,解答此題需要具備統籌思想,將想象、聯想、分析、類比、整合以及推理有效地應用到解題過程匯總,以此鍛煉學生的思維探究能力,因此具有很高的價值,值得以后模擬訓練及探究性學習。
二、考試原題:2015 年高考福建卷文科第I 卷,第21 題
(Ⅰ)求函數f(x)的最小正周期;
(1)求函數g(x)的解析式;
(2)證明:存在無窮多個互不相同的正整數x0,使得g(x0)>0.
(一)點評
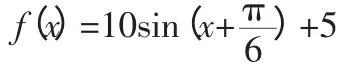
想要證明存在無窮多個互不相同的正整數x0,使得g(x0)>0,可解不等式g(x0)>0,只需解集的長度>1,此時解集中一定含有整數,由周期性可得,一定存在無窮多個、且互不相同的正整數x0.
(二)試題解析
所以g(x)=10sinx-8.
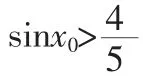
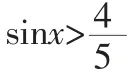
三角函數主要考查的是三角函數的單調性、周期性、奇偶性以及最值問題,同時還結合三角函數的圖像、三角恒等變換、函數模型的應用、正余弦定理及其應用以及平面向量及其應用。結合以上考試中的常見問題,可以回顧以往高考試卷中關于三角函數的相關試題。
三、問題回顧
例1.若x 是三角形的最小內角,則函數y=sinx+cosx+sinxcosx的最大值是 ( )
分析:三角函數的最值問題是三角函數常見的考查內容之一,主要是利用正余弦定理的有界性,通過換元或是其他方法的三角恒等變換來轉化問題。本題中三角形的最小內角是不大于的,而(sinx+cosx)2=1+2sinxcosx,可通過換元解決.
點評:涉及sinx±cosx 與sinxcosx 的問題時,通常用換元解決.
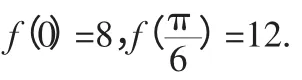
(1)求實數a,b 的值;(2)求函數f(x)的最大值及取得最大值時x 的值.
分析:利用待定系數求a,b,可以利用倍角公式和降冪公式進行問題的轉化.
解析:函數f(x)可化為f(x)=asin2x+bcos2x+b.
綜上所述,三角函數問題是高考中的常見問題,在解題過程中會運用多種相關知識,這些問題綜合性強,方法靈活多樣,并且問題本身并不是割裂和獨立的,而是相互聯系和依存的,通過不同的解題方法,動態地、辯證地看待解決問題,充分利用和調動相關知識,在熟練掌握公式的基礎上,融入一些數學思想,輔以一些解題技巧,運用綜合分析,嘗試從多角度解答問題,拓展思路,發散思維,不斷積累經驗,關鍵時刻問題就能迎刃而解。由此可見,對2015 年福建省高考試卷中的三角函數進行剖析和探究,可以集思廣益、舉一反三,觸類旁通,同時引導學生加強合作交流,積極探索并分享經驗,可以提高學生的學習效率,為以后的學習和考試打下堅實的基礎。

