小波分析在激光測距傳感器中的應用

薛纏明，李麗宏

(太原理工大學 信息工程學院，山西 太原030024)

0 引 言

目前，國家對車輛超限的治理已有了嚴格的要求。此前在車輛寬高超限檢測中都是靠人工測量完成，不僅影響車輛的行駛進度，而且測量效率較低。為了精確快速地檢測車輛的寬高和提高道路的暢通性，開發了單傳感器激光車輛寬高檢測系統。在使用的過程，發現測量信號中摻雜有高頻車輛邊緣光噪聲，導致測量精度明顯下降［1］。甚至會影響到車輛是“正常”還是“超寬超高”的判斷和車輛的正常通行。小波分析具有多分辨率分析的特點，并在時域和頻域都具有表征信號局部特性的能力［2］。

針對上述出現的問題，本文提出以小波分析法為基礎利用邊緣光噪聲的特性準確定位出光噪聲的精確范圍，進一步有效地去除它對車輛準確性測量的影響。

1 激光車輛寬高檢測系統

激光車輛寬高檢測系統如圖1 所示，激光傳感器發射激光遇到被測物體后發生反射，傳感器接收到反射光，經過計算得出被測物體位置的極坐標［3］。該激光車輛寬高檢測系統是把激光傳感器安裝在龍門架中間，經過實驗合理設置傳感器掃描角度和分度。當有車輛進入檢測區域時，激光傳感器以50 Hz 的頻率掃描，每個周期可以得出一組車輛的寬度和高度值，當汽車完全通過時，通過比較所有數值得出車輛的最寬值和最高值計入數據庫。

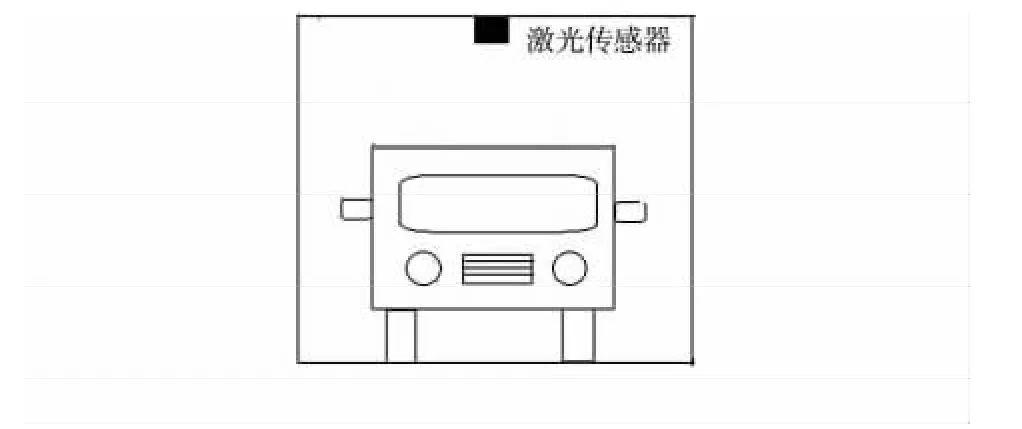
圖1 激光車輛寬高檢測系統圖Fig 1 Laser width-height detection system of vehicle

2 小波分析法

目前在系統信號檢測中小波分析方法憑借它在時域和頻域同時具有良好的空間局部化性質，已經成為信號檢測的重要工具。在實際的信號中，噪聲通常表現為高頻信號，而有用信號通常表現為低頻或者平穩信號［4］。基于上述噪聲信號的特性，可以利用小波變換通過伸縮平移運算對信號逐步進行多尺度細化，在高頻處利用時間細分和可以聚焦在任意高頻細節的優點，對原始信號進行小波分析和噪聲信號的定位。在利用小波分析對原始信號去除噪聲過程中，最理想的結果是有效地保留有用信息，且去除摻雜的干擾噪聲，所以，在小波分析中小波函數和閾值的選擇變成了關鍵環節。為此，提出一種以小波分解為基礎去除噪聲的方法，其可分為三個步驟:

1)對測量信號作小波分解

選擇一個小波的基函數ψ(t)和小波分解中小波系的階數D，其中，ψ(t)為平方可積，即ψ(t)∈L2(R)，對原始信號進行D 階分解后，可以利用鼻尖細節部分準確定位出高頻信號的范圍。

2)光噪聲定位

對原始信號進行D 階分解后，根據噪聲信號的幅值和頻率特性，對信號細節部分進行閾值判斷，準確地判別出光噪聲在信號中的具體范圍。

3)數據檢測

對信號進行小波分解和高頻光噪聲準確定位后，對信號進行重構出完整的有用信息。通過Matlab 仿真，便可直觀地看到重構后信號。

2.1 小波函數選擇與分解

在激光寬高檢測系統中，車輛實際信號通常表現為低頻信號或是一些比較平穩的信號，而邊緣光噪聲則通常表現為特定的高頻信號。Daubechies 小波是由世界著名的小波分析學者Inrid Daubechies［5］構造的小波函數，應用它對原始信號進行分解時隨著階次增大，消失矩階數越大，頻帶劃分效果越好，并且提供了比其它函數更有效的分析和綜合能力［6］。

設原始信號為f(t)，它的序列為{f(t)，n=1，2，…，N}。若以{f(n)，n=1，2，…，N}表示信號f(t)在尺度j=0 時的近似值，A0(n)=f(n)，則f(t)的小波變換由以下兩個公式確定

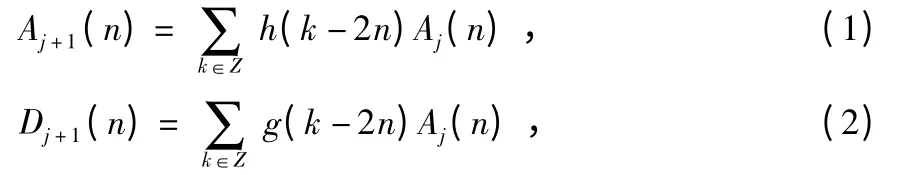
式中 h(n)和g(n)為由小波函數ψ(t)確定的一對互補的共軛濾波器，其中，h(n)為低通濾波器，g(n)為高通濾波器。因而，Aj，Dj分別稱為信號在尺度j 上的逼近部分(低頻)和細節部分(高頻)。離散信號A0經過尺度1，…，j 的分解，最終分解為D1，D2，…，Dj，Cj它們分別包含了信號從高頻到低頻的不同頻帶信號，即信號的小波的分解就是相當于信號不斷經過兩個低通和高通濾波器對其近似部分進行濾波的結果。

對于三級分解，原始信號f(t)可分為

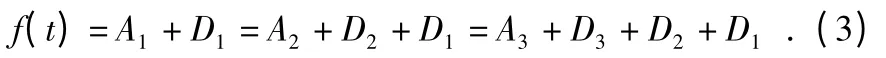
結合激光寬高檢測系統實際使用得出的噪聲頻率特性，選擇利用Daubechies 小波進行三級分解。

2.2 光噪聲的定位

光噪聲是指對于車輛實際值的隨機偏離。利用小波分析法窗口面積固定，但形狀可以改變，在低頻部分具有較高的頻率分辨率和較低的時間分辨率，在高頻部分具有較高的時間分辨率和較低的頻率分辨率的特點。對原始信號進行小波分解后，在大尺度下，可以將信號的低頻信息(全局)表現出來，在小尺度下，可以將信號的高頻(局部)特征反映出來。

基于上述原理，通過跟蹤小波變換在細尺度下的模極大曲線方法檢測原始信號中高頻信號的位置;再根據實際實驗中光噪聲的幅值與車輛實際平穩信號幅值偏差閾值Δδ≤300 和車輛邊緣的位置來準確判斷光噪聲的范圍。

2.3 數據檢測

以山西某國道超限檢測站車輛數據為例，取出車輛通過激光車輛寬高檢測系統時采集的一個周期的數據，通過小波分解和光噪聲定位后，對處理后的信號進行重構，采用Matlb 中利用工具箱函數利用wavedec()函數進行小波分解仿真實驗［7］。wavedec()的調用格式為

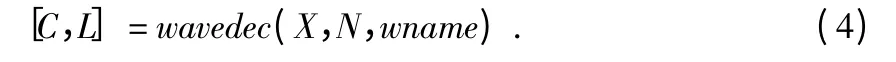
其中，［C，L］為小波分解輸出值，X 為一維信號，N 為分解的層數，wname 為使用的小波函數。原始信號如圖2所示。

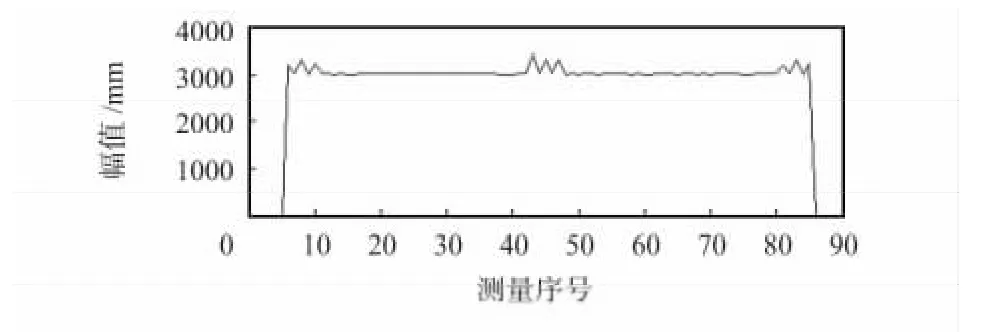
圖2 原始信號Fig 2 Original signal

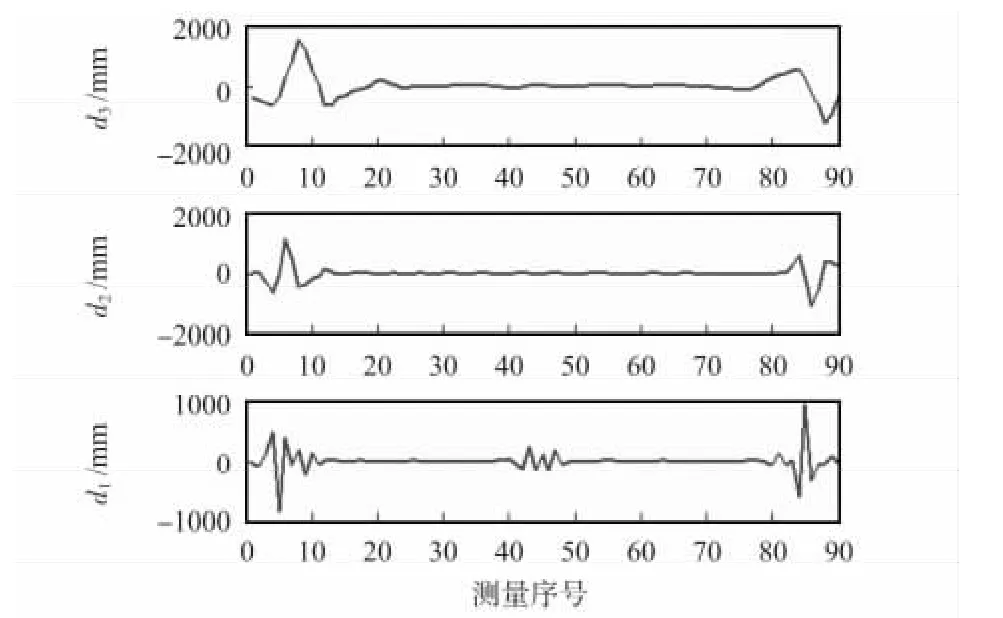
圖3 用db3 小波進行5 層分解后的第1 ～3 層細節系數Fig 3 Detail coefficients of 1 ～3 layers after decomposition 5 layers with db3 wavelet

對原始信號小波三級分解后的第1 ～3 層細節系數，如圖3 所示。經過三級分解，發現在第1 層細節系數d1中明顯定位出高頻信號的位置，再利用實驗得到的幅值偏差閾值Δδ≤300 進行判斷，如果定位出的位置幅值在偏差閾值范圍內，且在車輛信號的邊緣，便可認為是光噪聲;否則，認為是車輛的實際高頻信號，最后去除判斷出的范圍，對信號進行重構，得到重構后的信號如圖4。

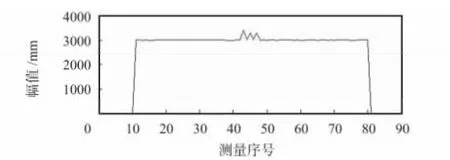
圖4 重構后的信號Fig 4 Reconstructed signal

3 結 論

本文將小波分析理論應用到智能測量寬高檢測系統中，經過仿真和實際使用，對原始信號進行小波分解、閾值判斷和重構。結果表明:小波分析法可以有效地消除高頻光噪聲的影響，有利于提高系統的精度。

［1］ 李永強，盛業華，劉會云，等.激光掃描點圖像背景交互式濾除［J］.測繪科學，2008(1):130－250.

［2］ 權愛娟.小波分析在一維奇異信號檢測應用中的應用研究［D］.德州:德州學院，2012.

［3］ 陳元朝，李麗宏.自適應濾波算法在車輛寬高檢測系統中的應用［J］.中國測試，2014(2):40－43.

［4］ 張小飛，徐大專，齊澤鋒.基于小波變換奇異信號檢測的研究［J］.系統工程與電子技術，2003(7):814－855.

［5］ Ingrid Daubechies.Ten lectures on wavelets［C］∥CBMS－NSF Regional Conference Series in Applied Mathematics，Philadelphia:SIAM ED，2007:56－62.

［6］ 劉正平，馮召勇，楊衛平.基于小波去噪的微弱信號提取［J］.制造業自動化，2010(8):98－101.

［7］ 董長虹.Matlab 小波分析工具箱原理及應用［M］.北京:國防工業出版社，2009.