HHT 邊際譜熵在單相自適應重合閘中的應用

戴永梁，黃 純，羅勛華，唐曉勇，孫彥廣，賈天云

（1.湖南大學電氣與信息工程學院，長沙410082；2.冶金自動化研究設計院，北京100071）

自動重合閘技術在超高壓輸電線路上得到了廣泛應用，其目的是為了在瞬時性故障消除后使線路重新投入運行。由于絕大部分故障是單相瞬時性的，所以自動重合閘提高了電力系統并列運行的穩定性和供電的可靠性。然而，發生永久性故障時重合閘會給電力系統造成很多不利影響[1]。因此，若能在重合閘之前就正確判斷出是瞬時性或是永久性故障，再決定是否重合閘，具有非常重要的意義。

近年來，單相自適應重合閘的理論和方法日趨成熟。自適應重合閘主要方法有電壓判別法[2]、智能識別法[3-4]、小波分析法[5-7]以及經驗模態分解法[8-9]等。其中，電壓判據法在永久性接地故障發生在端口的出口處時常有誤判；基于神經網絡的智能識別法需要一定量的樣本，且識別系統有黑匣子的特征，難以對其進行相對的直觀理解和定量分析；小波分析法依賴小波基的選擇，選擇的小波基不同，則分析的結果也不盡相同[10]。

HHT（Hilbert-Huang transform）方法是一種非平穩、非線性信號的自適應時頻分析方法。HHT 以經驗模態分解EMD（empirical mode decomposition）方法和Hilbert 變換為基礎，可以得到較高的時頻分辨率，具有良好的時頻聚集性[10]。信息論中的主要信息測度指標包括復雜性測度（如近似熵等）和信息熵測度（如廣義信息熵等）兩種[11]，結合HHT和信息測度特點可以進一步開拓其在電力系統故障識別和檢測的應用潛力。文獻[9]運用EMD 分解和近似熵實現故障信號時域的復雜性測度并識別故障性質，但判別時間較長且受模式維數和容限的影響[11]。

與時域表示相比，信號的頻域表示往往更能體現信號的本質特征[12]。文獻[13]刻畫了動態信號頻域復雜度特征的HHT 邊際譜熵應用于心率變異分析并獲得成功。

本文利用HHT 邊際譜熵對輸電線路單相故障的故障相端電壓信號進行分析，通過比較故障相端電壓的邊際譜熵值來快速區別永久性故障和瞬時性故障。不僅開辟了EMD 與邊際譜熵結合并實現了其在頻域中的復雜性識別，同時也縮短了其識別時間，可靠性高。仿真實驗驗證了所提方法的可行性和有效性。

1 HHT 邊際譜熵的原理

1.1 HHT

HHT 分兩部分：EMD 和Hilbert 變換。EMD 根據信號自身的時間尺度，把任何一個信號x（t）自適應的分解為有限個窄帶信號，稱為固有模態分量IMF（intrinsic mode function）[14]，即

式中：ci（t）為IMF 分量；rn（t）為殘余函數。

對每一個IMF 分量ci（t）作Hilbert 變換，有

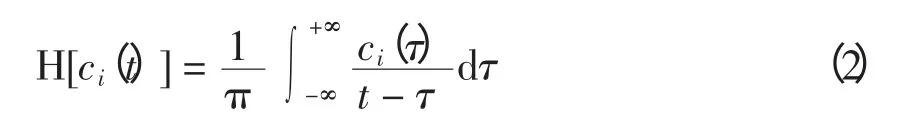
構造解析信號

則

式中：Re 表示取實部；n 為IMF 分量的個數；ai（t）、φi（t）、fi（t）分別為瞬時幅值、瞬時相位、瞬時頻率。忽略了殘余函數rn（t）。

Hilbert 變換得到的幅值和頻率都是時間的函數，故可將信號幅值在三維空間中表示成時間和頻率的函數H（f，t），稱為Hilbert 幅值譜，即

將H（f，t）對時間積分，即可得到Hilbert 邊際譜，即

式（6）描述了信號的幅值隨頻率的變化規律。

1.2 HHT 邊際譜熵

Shannon 將熵的概念引到了信息論中，定義信息熵作為某事件的不確定性量度，被普遍用來衡量信號的復雜性和不規則性。在信號處理領域中，信號越復雜越不規則，則熵值越高；信息越規則，熵值越低；若信號完全確定，則熵值為0。

在離散的頻率點f=iΔf，式（6）變為

式中：J 為信號在分析頻帶內的頻率離散點數；T 為信號的時間長度。

HHT 邊際譜熵定義[13]為

式中，pi=h（i）/Σh（i），表示第i 個頻率對于幅值出現的概率。熵值歸一化為0～1，則有

式中，L 為h（i）的序列長度。

HHT 邊際譜熵表示信號在頻域上的不確定性，可用來作為信號頻率復雜度的一種量度。信號在整個頻率成分上分布越均勻、信號越復雜，不確定性程度就越大。

2 HHT 邊際譜熵的特性分析

為了分析HHT 邊際譜熵對不同電力信號的辨別能力，定義如圖1 所示的4 種信號，即

式中，N 為均值為0、方差為1 的高斯白噪聲。設采樣頻率為20 kHz，時間窗為40 ms。

圖1 4種信號的波形Fig.1 Waveforms of four signals

圖2為4 種信號的邊際譜。

（1）分別計算y1～y4各信號的HHT 邊際譜熵，結果如表1 所示。

圖2 4 種信號的邊際譜Fig.2 Marginal spectra of four signals

表1 4 種信號的HHT 邊際譜熵Tab.1 Marginal spectra entropy of four signals

表1 中，y1只含單一頻率的信號，是一種平穩而規則的信號，故其HHT 邊際譜熵很小；y2含有2種頻率成分的信號，比y1復雜，其HHT 邊際譜熵也比y1大；y3含有3 種頻率成分的信號，故其HHT邊際譜熵較y2大；y4含有高斯白噪聲，頻譜更為復雜，其HHT 邊際譜熵明顯高于其他信號。由此可見，HHT 邊際譜熵與信號頻率的復雜程度有關，頻率成分越復雜，HHT 邊際譜熵越大。

（2）改變y4中高斯白噪聲的混入比值，再分別計算信號的HHT 邊際譜熵，結果如表2 所示。

表2 改變噪聲比值后的信號邊際譜熵Tab.2 Marginal spectrum entropy with different noise

比較表1 與表2 可知，當信號中噪聲比例較小時，HHT 邊際譜熵與不含噪聲時的HHT 邊際譜熵相近，這表明HHT 邊際譜熵具有一定的抗干擾能力；但當噪聲含量較大時，其HHT 邊際譜熵也較大，可見HHT 邊際譜熵對較大噪聲是很敏感的，因此用HHT 邊際譜熵對信號進行分析時，應保證一定的信噪比。

（3）改變y1信號的采樣時間窗分別為40 ms、45 ms、50 ms、55 ms、60 ms、200 ms、500 ms、1 s，計算結果如表3 所示。

表3 不同時間窗的y1 的HHT 邊際譜熵Tab.3 Marginal spectrum entropy with different time windows

由表3 可知，當時間窗為信號y1工頻周期的整數倍時，信號的HHT 邊際譜熵為0，表明該信號頻率成分是完全確定的。當時間窗不是工頻周期的整數倍時，信號的邊際譜熵也都很小且接近于0，故其跟采樣時間窗有關但影響不大。所以若要取得較好分析結果，應盡量選采樣時間窗為其工頻周期的整數倍。

通過以上分析可知，HHT 邊際譜熵能夠反映信號的頻率復雜程度，具有一定的抗噪聲能力，本文嘗試將其應用于電力故障信號的分析。

3 基于HHT 邊際譜熵的故障性質識別及其仿真研究

3.1 單相永久性故障時的斷開相端電壓

當輸電線路發生故障后，故障相兩端斷路器斷開，由于故障相與非故障相之間存在電容和電磁耦合的影響，會使故障點電弧在一定時間范圍內仍然流有潛供電流[15]。

當線路發生永久性故障時，在斷路器斷開后，由于故障點一直存在，線路中的儲能元件和分布電容對地迅速放電，使電弧很快熄滅，一般持續時間為2～4 個工頻周期，期間由于處在燃弧階段，所以頻率成分相對復雜。電弧熄滅后，因其斷開相恢復電壓中沒有自由分量，只含工頻分量[16]，所以頻率成分單一。

3.2 單相瞬時性故障時的斷開相端電壓

當線路發生瞬時性故障時，在斷路器斷開后，由于故障點將在一段時間內持續流過潛供電流，即進入二次電弧階段。在該階段受多種因素的影響，電弧的重燃電壓會不斷增大。當故障點對地的電壓小于重燃電壓時，電弧電流變得很小，相當于電弧的熄弧狀態；隨著故障點對地電壓的迅速增大，當故障點對地電壓大于重燃電壓時，電弧會再次燃燒，直到故障點對地電壓的大小不能夠使電弧重燃時，故障電弧才真正熄滅[17]。在此，二次電弧期間將產生很多復雜的高頻暫態信號，即含有除工頻分量外還有很多復雜高頻分量，且二次電弧持續大概10 個工頻周期[18]時長。

3.3 單相自適應重合閘原理及實現步驟

由以上分析可知，在斷路器斷開后的大概10個工頻周期內，即瞬時性故障二次電弧存在期間，由于永久性故障燃弧時間比較短，在電弧熄弧后，其恢復電壓中只含有單一頻率的工頻電壓信號，固其故障相端電壓的HHT 邊際譜熵近似為0；而瞬時性故障在斷路器斷開后的二次電弧階段故障相端電壓的頻率比較復雜，故障相端電壓的HHT邊際譜熵遠大于0。利用在不同性質故障下故障相端電壓的HHT 邊際譜熵的這種特性差異，可以設定個合理的閾值來判別故障性質。由此，斷路器斷開后，永久性故障相電壓中所含的高頻電壓會很快衰減，之后的恢復電壓只含工頻分量，所以為了提高精度減少誤差，采樣時間窗選1 個工頻周期20 ms。

具體的單相自適應重合閘實現步驟如下。

步驟1 對斷路器跳閘后的故障相端電壓信號進行提取，對每個工頻周期（20 ms）內的數據進行HHT 邊際譜熵的計算，連續采樣H 個工頻周期。H 一般應小于10，那是因為瞬時性故障的二次電弧持續時間一般為200 ms，而永久性故障在電弧熄滅后，一般為2～4 個周期會很快進入恢復電壓階段。由于永久性故障斷路器跳開后的開始階段會持續一段短時的燃弧階段，因此其HHT 邊際譜熵和瞬時性故障的值一般區別不大，在恢復電壓階段由于只有單一頻率的電壓，永久性故障的HHT 邊際譜熵接近0，而瞬時性故障因在二次電弧階段，有很多復雜的高頻信號，其HHT 邊際譜熵會遠大于0。所以采樣周期H 應大于3～4 為最佳，本文采用8 個工頻周期。

步驟2 對H 個邊際譜熵與閾值Pset相比較來快速區分故障性質。若H 個邊際譜熵都大于閾值Pset，則判斷為瞬時性故障；反之，若在H 個邊際譜熵中只要有一個小于閾值Pset，則判斷為永久性故障。

3.4 仿真系統介紹

本文利用常見的ATP（alternative transients program）程序是電磁暫態分析程序EMTP（electromagnetic transients program）最廣泛的一個使用版本，簡稱ATP-EMTP。本文利用ATP 程序對某750 kV帶并聯電抗器的輸電線路進行仿真研究，其線路模型如圖3 所示[19]，電弧模型采用文獻[1]模型。

圖3 750 kV 輸電線路仿真模型Fig.3 750 kV transmission line model

線路參數分別為：R1= 0.016 25 Ω/km，R0=0.157 23 Ω/km，L1= 0.905 64 mH/km，L0= 1.945 54 mH/km，C1=0.013 26 μF/km，C0=0.010 06 μF/km。ZLm=10+j942 Ω，Znm=1+j94.2 Ω，ZLn=20+j188 4 Ω，Znn=0。

仿真參數設置為：Em、En的相角差為20°，ATPEMTP 采樣頻率為20 kHz。以A 相故障為例，線路在50 ms 時發生接地故障，100 ms 時線路兩端斷路器跳開，300 ms 時電弧熄滅，800 ms 時進行重合閘。圖4 為線路中點發生瞬時性故障和永久性故障時，在線路首端得到的故障相電壓波形。

3.5 基于HHT 邊際譜熵的故障性質識別

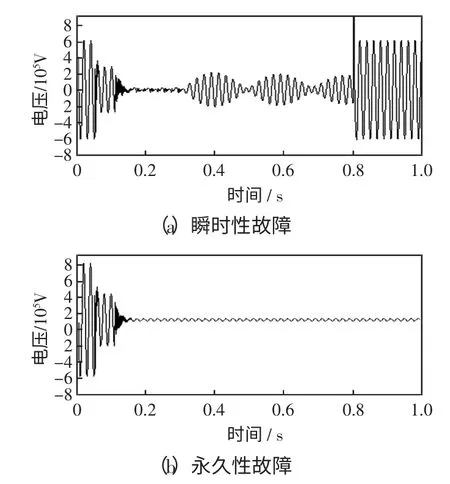
圖4 故障相端電壓波形Fig.4 Voltage waveform of fault phase

本文對斷路器斷開后故障相端電壓連續采樣8 個工頻周期，對每個工頻周期內的數據進行一次HHT 邊際譜熵計算。大量仿真結果顯示：在8 個工頻周期內，瞬時性故障時的故障相端電壓HHT 邊際譜熵各不相同且都比較大，值均高于閾值Pset，但熵差異并不大。而永久性故障時的故障相端電壓HHT 邊際譜熵在前幾個周波內的值相對比較大且高于閾值Pset，但之后的幾個周波內熵基本趨于0，遠低于閾值Pset。因此，可以確定一個較大裕度的HHT 邊際譜熵閾Pset=0.15，同時得出判斷故障性質的判據為

計算得到8 個故障相電壓的HHT 邊際譜熵均大于閾值Pset，則判斷為瞬時性故障；否則為永久性故障。

表4～表9 為圖3 所示系統在不同故障點、不同過渡電阻情況下各周波故障相端電壓的HHT 邊際譜熵值（故障相端電壓以線路m 端為例）。

表4 金屬性短路永久性故障的邊際譜熵值Tab.4 Marginal spectrum entropy of permanent metallic short circuit fault

由表4～表9 可知，HHT 邊際譜熵算法不受故障位置及過渡電阻的影響，同時，在斷路器跳開后，瞬時性故障時故障相端電壓信號的頻率成分比永久性故障時要復雜的多，HHT 邊際譜熵的信息熵測度算法能可靠地在8 個周波內快速區分線路故障性質。

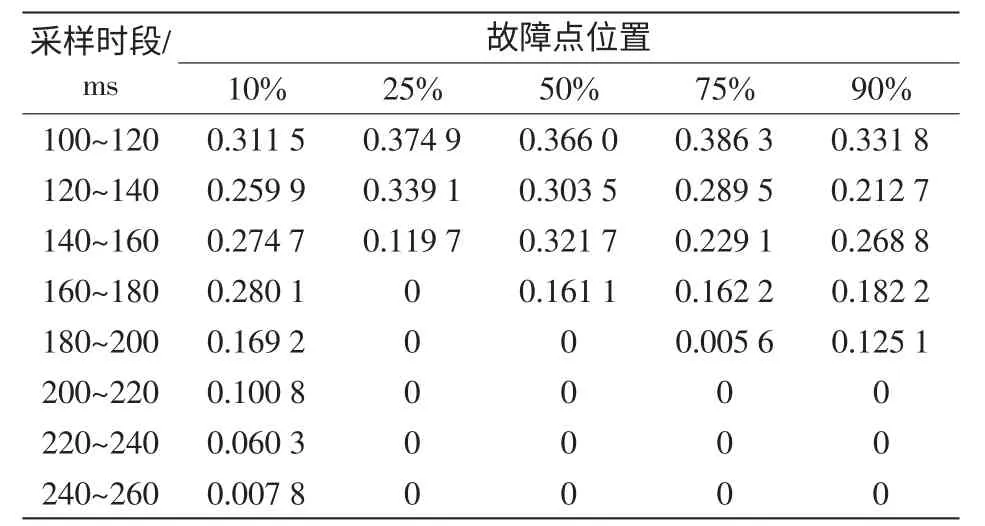
表6 經10 Ω 過渡電阻永久性故障的邊際譜熵Tab.6 Marginal spectrum entropy of 10 Ω transition resistance with permanent fault

表7 經10 Ω 過渡電阻瞬時性故障的邊際譜熵Tab.7 Marginal spectrum entropy of 10 Ω transition resistance with transient fault

表8 經100 Ω 過渡電阻永久性故障的邊際譜熵Tab.8 Marginal spectrum entropy of 100 Ω transition resistance with permanent fault

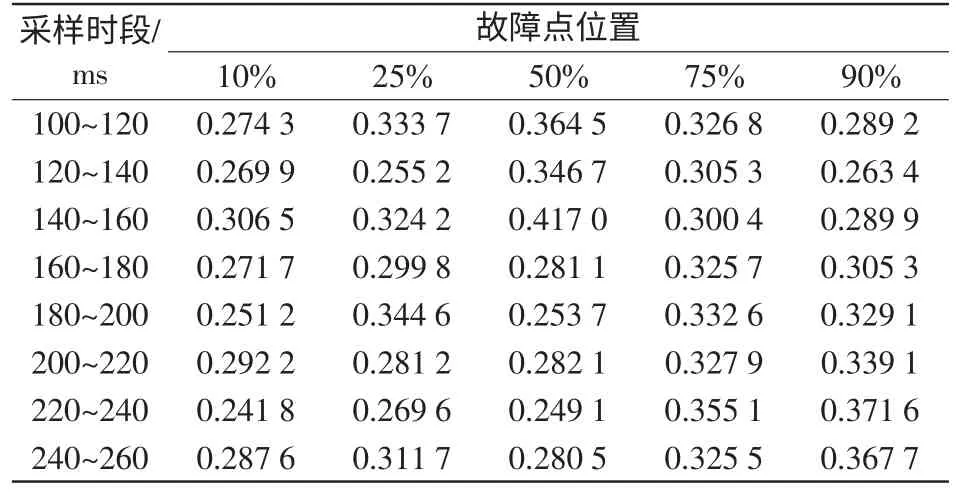
表9 經100 Ω 過渡電阻瞬時性故障的邊際譜熵Tab.9 Marginal spectrum entropy of 10 Ω transition resistance with transient fault

3.6 本文方法與其他EMD 及熵結合方法的比較

本文對文獻[9]中提到的EMD 與近似熵結合方法進行比較。取模式維數m=2，容限r=0.2SD（SD 為信號序列的方差）。現只對經10 Ω 的過渡電阻的輸電線路中點位置故障進行分析，其中IMF1～IMF4的近似熵記為E1～E4[8]，E1～E4的和為E。結果如表10 和表11 所示。

表10 經10 Ω 過渡電阻中點瞬時性故障的近似熵Tab.10 Approximate entropy of 10 Ω transition resistance with transient fault

表11 經10 Ω 過渡電阻中點永久性故障的近似熵Tab.11 Approximate entropy of 10 Ω transition resistance with permanent fault

由表10、表11 可知，若采樣時間短即數據點太少的話，以近似熵和為1 為界限區分不了瞬時性和永久性故障。采樣時間相對長些，即200 ms 左右（電弧時間）的話，可以區分出永久性和瞬時性故障的，但差距不是很大。而HHT 邊際譜熵的話，一般8 個工頻周期（160 ms）左右可以可靠地區分出故障性質。若更快的話，只要連續計算出的HHT邊際譜熵只要有一個低于閾值就判別的話，一般6個工頻周期（120 ms）以內就可以判斷出。由此可見，雖然EMD 與近似熵結合的分析方法可以相對可靠地檢測出故障性質，但其采樣時間比較長，相比較而言，用HHT 邊際譜熵的分析方法可以用較短的數據相對更快速地檢測出故障性質，且也不用像近似熵一樣還要考慮不同的模式維數m 和容限閾值r 的影響[11]。

4 結論

（1）對HHT 邊際譜熵的特性進行了分析，研究表明其能夠很好地反映信號頻率的復雜程度并具有一定的抗干擾能力。

（2）對瞬時性故障和永久性故障的故障相端電壓信號的頻域復雜性及邊際譜熵特性差異進行了分析，提出了基于HHT 邊際譜熵的自適應重合閘判據，即對斷路器跳閘后的故障相端電壓進行HHT 邊際譜熵計算，比較該熵值與閾值Pset的大小。若熵都大于閾值Pset，則判斷為瞬時性故障；反之，則判斷為永久性故障。

（3）本文為輸電線路單相接地故障的故障性質診斷提供了一種有效的頻域信息熵測度分析方法。該方法可以用較短的數據快速有效判斷出故障性質，一般可在6～8 個工頻周期內作出判斷，提高了重合閘的成功率，且不受故障位置、過渡電阻等因素影響。

（4）ATP-EMTP 故障仿真結果驗證了本文方法的可行性和有效性。

[1]程玲，徐玉琴，宋秭霖（Cheng Ling，Xu Yuqin，Song Zilin）.基于電弧小波譜能量分析的輸電線路單相自適應重合閘（Single-pole adaptive reclosure of transmission line based on arc models and wavelet spectrum energy analysis）[J]. 電網技術（Power System Technology），2007，31（24）：81-85.

[2]葛耀中（Ge Yaozhong）.在單相自動重合閘過程中判別瞬時故障和永久故障的方法（Method of distinguishing between instant and permanent faults during automatic single-phase reclosing）[J].西安交通大學學報（Journal of Xi'an Jiaotong University），1984，18（2）：23-31.

[3]房鑫炎，闕波（Fang Xinyan，Que Bo）.人工神經網絡在自適應重合閘瞬時與永久故障判別中的應用（The application of ANN in the distinction of transient and permanent faults during adaptive autoreclosure）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），1999，11（3）：80-85，90.

[4]楊偉，彭麗，張俊芳，等（Yang Wei，Peng Li，Zhang Junfang，et al）. 基于模糊神經網絡的自適應單相自動重合閘（Adaptive autoreclosure of single phase based on FNN）[J].繼電器（Relay），2005，33（15）：66-70.

[5]林湘寧，劉沛，程時杰（Lin Xiangning，Liu Pei，Cheng Shijie）.超高壓輸電線路故障性質的復值小波識別（Identification of the instant faults occurred on the extra high voltage transmission line with a complex wavelet algorithm）[J].中國電機工程學報（Proceedings of the CSEE），2000，20（2）：33-38.

[6]蔡超豪（Cai Chaohao）.基于小波包變換的自適應重合閘（Adaptive auto-reclosing for transmission line based on wavelet packet transform）[J]. 繼 電 器（Relay），1999，27（2）：21-23.

[7]黃娟，黃純，江亞群，等（Huang Juan，Huang Chun，Jiang Yaqun，et al）.基于小波包近似熵的線路故障性質辨識方法（Identification method of fault characteristics in transmission lines based on wavelet packet and approximate entropy）[J].儀器儀表學報（Chinese Journal of Scientific Instrument），2012，33（9）：2009-2015.

[8]蘭華，艾濤，李揚（Lan Hua，Ai Tao，Li Yang）.經驗模態分解在單相自適應重合閘中的應用（Application of EMD on single-pole adaptive reclosure of transmission）[J].電力系統保護與控制（Power System Protection and Control），2010，38（12）：35-39.

[9]蘭華，艾濤，張桂蘭（Lan Hua，Ai Tao，Zhang Guilan）.基于經驗模態分解及近似熵的輸電線路單相自適應重合閘（Single-phase adaptive reclosure of transmission lines based on EMD and approximate entropy）[J]. 電 網 技 術（Power System Technology），2009，33（20）：211-214.

[10]鐘佑明（Zhong Youming）.希爾伯特-黃變換局瞬信號分析理論的研究（Research on the Local-instantaneous Signal Analysis Theory of the Hilbert-Huang Transform）[D].重慶：重慶大學機械工程學院（Chongqing：College of Mechanical Engineering，Chongqing University），2002.

[11]符玲（Fu Ling）.基于信息測度的電力系統故障識別方法研究（Information Measurement Based Fault Discrimination in Power System）[D].成都：西南交通大學電氣工程學院（Chengdu：School of Electrical Engineering，Southwest Jiaotong University），2010.

[12]Shie Qian，Chen Dapang.Joint time-frequency analysis[J].IEEE Signal Processing Magazine，1999，16（2）：52-67.

[13]董紅生，邱天爽，張愛華，等（Dong Hongsheng，Qiu Tianshuang，Zhang Aihua，et al）.基于HHT 邊際譜熵和能量譜熵的心率變異信號的分析方法（The analysis method of heart rate variability signal based on the HHT marginal spectrum entropy and energy spectrum entropy）[J]. 中 國生物醫學工程學報（Chinese Journal of Biomedical Engineering），2010，29（3）：336-344.

[14]Norden E H，Zheng Shen，Steven R L，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society，1998，454（1971）：903-995.

[15]李博通，李永麗（Li Botong，Li Yongli）.基于潛供電流計算的輸電線路單相永久性故障判斷方法（Identification method for single phase permanent fault based on calculation of secondary arc current on transmission line）[J]. 天津大學學報（Journal of Tianjin University），2010，43（5）：424-428.

[16]曹芬（Cao Fen）.高壓輸電線路自適應重合閘技術研究（Research on Adaptive Reclosing Technique for HV Transmission Lines）[D]. 杭州：浙江大學電氣工程學院（Hangzhou：College of Electrical Engineering，Zhejiang University），2010.

[17]Ban G，Prikler L，Banfai G. Testing EHV secondary arcs[C]//IEEE Porto Power Tech Conference. Porto，Portugal，2001.

[18]Ahn Sang-Pil，Kim Chul-Hwan，Agganrwal R K，et al. An alternative approach to adaptive single pole auto-reclosing in high voltage transmission systems based on variable dead time control[J].IEEE Trans on Power Delivery，2001，16（4）：676-686.

[19]吳文輝，曹祥麟.電力系統電磁暫態計算與EMTP 應用[M].北京：中國水利水電出版社，2012.