風電場短期功率預測

楊曉萍，王寶，蘭航，武小暄（西安理工大學水利水電學院，西安710048）

風電場短期功率預測

楊曉萍，王寶，蘭航，武小暄
（西安理工大學水利水電學院，西安710048）

風電場輸出功率的預測對大規模風電接入電力系統運行有非常重要的意義。針對現有各種預測方法預測精度不高的問題，提出了一種基于相關向量機－馬爾科夫鏈的風電短期功率預測方法。首先，運用相關向量機原理，得到原始預測模型；之后，使用馬爾科夫鏈原理對誤差進行修正，結合最小二乘法得到風電場短期功率預測-誤差修正模型；最后，將該方法用于實際風電場的短期功率預測，其平均相對誤差達到7.2%。研究結果表明：所提的預測方法能夠滿足電力系統調度對風電場短期功率預測的要求。

風電場；短期功率；預測；相關向量機；馬爾可夫鏈

風能作為一種清潔的可再生能源，得到各國的重視和開發利用，但大規模風電機組的接入會嚴重影響電力系統的正常運行。因此，研究風電場發電功率的預測對電力系統調度有著非常重要的意義。

對風電功率的預測分為中長期、短期、超短期預測。目前，風電功率的短期預測的方法有2種：物理和統計方法。物理方法是根據天氣預報數據通過數學關系計算風電場的出力數據，繪出功率預測曲線圖；統計方法是根據歷史數據與風電場出力之間的關系，建立預測模型，通過預測參數，預測風電場的發電功率。物理方法的預測精度受風電場的物理條件影響很大，統計方法的預測精度較高。因此，國內外主要采用統計方法[1]。

目前，風電功率短期預測的統計方法主要有：時間序列[2]、灰色理論[3]、神經網絡NNS（neural networks）[4-5]、支持向量機SVM（support vectormachine）[6-7]。時間序列方法簡單但其預測誤差大；灰色理論預測模型多樣，但預測結果是一個區間，無法獲得一個精確值；神經網絡方法，拓撲結構緊湊，與前兩種方法相比其預測精度較高，但是需要大量的歷史數據，訓練時間長；支持向量機方法簡單，魯棒性能好，預測精度比神經網絡高，但是核函數的選擇條件要求嚴格、易出現過學習和局部最小值等問題。相關向量機RVM（relevance vector machine）是由Tipping提出的一種基于總體貝葉斯框架下的稀疏概率模型，是近來機器學習領域研究的熱點之一[8]。相關向量機具有與支持向量機相同的優點，但與支持向量機相比，其核函數的選擇比較靈活，引入超參數，降低了計算的復雜程度，所需的數據量遠小于支持向量機，具有非常高的稀疏性[9]。

預測誤差的產生是風電功率預測的必然結果，因此需要對誤差進行修正，提高預測精度。誤差修正的方法主要有：現成的誤差修正模型ECM（ready-error correctionmodel）[10]、自回歸滑動平均模型ARMA（auto-regressive andmoving averagemodel）[11]、局部模擬近似值、周期外推法、最小二乘法以及馬爾可夫鏈[12]等。最小二乘法和馬爾可夫鏈與前面幾種方法相比，精度較高，并且馬爾可夫鏈適用于描述隨機波動性大的問題。

本文運用相關向量機原理對風電場短期功率進行預測，并將最小二乘法于馬爾可夫鏈結合對預測誤差進行修正，建立基于時間尺度與精度尺度的風電場短期功率預測模型。并將該模型用于實際風電場的短期功率預測，與其他預測方法進行比較，預測結果說明本文所采用方法的有效性。

1 相關向量機基本理論

給定訓練樣本數據集合{xn，yn}，n=1，2，…，N，x為N維輸入向量，y為一維輸出向量。定義相關向量機的回歸模型為[13]

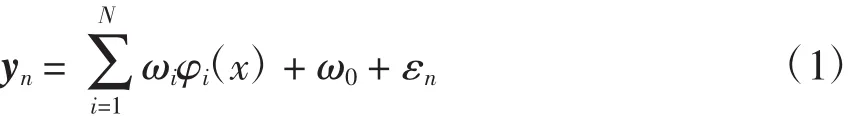
式中：ωi為權參數；ω0為權參數初始值；φi（x）為非線性基函數，φi（x）=K（x，xi），K（·）為選定的核函數。εn為均值為0的高斯噪聲，其方差為σ2。

假定輸出yn之間相互獨立，則給定的訓練集{xn，yn}的似然估計分布為

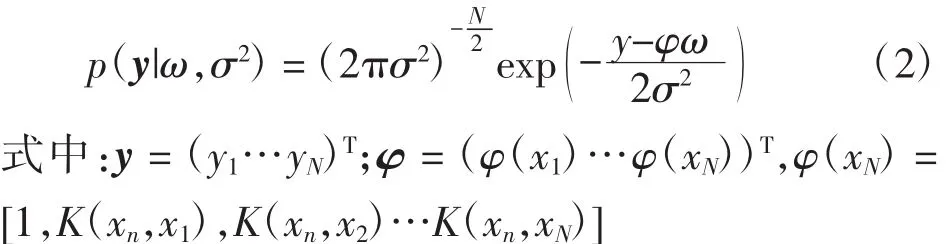
該模型中存在參數較多，如果采用最大似然估計函數求取權值ω和σ2方差，容易導致數據過擬合，在實際預測中應避免此問題發生[13]。因此，采用稀疏貝葉斯對ω賦予零均值高斯先驗概率分布，即

式中：α為滿足N+1維超參數分布的向量。這樣，每一個權重與一個超參數相對應，從而控制由于先驗分布而造成的參數變化，確保相關向量機的高稀疏性。

在先驗概率分布和似然分布的基礎上，求得所有未知參數的后驗概率分布為

其中，后驗協方差矩陣[13-15]分別為

為了確定模型的權值ω，必須求出超參數的最佳值，其迭代算法[12-14]為

式中：μi為第i個后驗平均權值；Nii后驗協方差矩陣；n為樣本數據個數。

如果給定新的輸入為x*，其對應輸出的概率分布服從高斯分布，即

式中，y*為x*對應的預測值，即y*=μTφ（x*）

2 馬爾可夫鏈的基本理論

馬爾可夫過程是一種隨機過程，具有無后效應，即未來狀態的變化不受過去各種狀態的影響。時間和狀態都離散的過程為馬爾可夫鏈[16]。

定義：隨機過程{x（tn-1），t∈T}，對任意有限的時間序列x（t1），x（t2），…，x（tn），對應的狀態a1，a2，…，an∈A，有

將該過程定義為馬爾可夫過程[17]。

定義：若隨機過程{x（t），t∈T}，對于任意整數和狀態a1，a2，…，an∈A的條件概率滿足

則該過程稱為馬爾可夫鏈。

條件概率p{xn=j|xn-1=i}表示系統n-1=i的條件下，時刻n轉移到狀態j的概率用一步轉移矩陣p表示，即

則k步轉移概率可由式p(k)=pk進行計算。

影響風電場發電功率的因素有：風速、風向、大氣壓強、溫度、大氣湍流、地形條件等。本文選取風速，溫度，大氣壓強組成三維樣本輸入數據，輸出為風電場預測功率。

基于相關向量機和馬爾可夫鏈的風電場短期功率預測過程分為模型訓練、模型測試以及模型修正3個階段。

1）模型訓練。

首先，選取樣本的原始輸入，將數據進行歸一化處理。處理方法[8-9]為

式中：x為歸一化后的數據；xi為歸一化前的數據；xmin為同組數據中的最小值；xmax為同組數據中的最大值。

其次，將歸一化處理后的數據，用貝葉斯概率論的相關原理（如式4）形成一次預測模型。檢驗平均相對誤差MAPE（meoMaverage relative error）是否達到要求，并以此作為該預測模型訓練過程的評價指標。

平均相對誤差MAPE表示為

式中：yi為第i次預測值；y為第i次實際值。

如果MAPE沒達到允許值，改變式（4）中的協方根誤差m值，再形成第2次，第3次，……，模型預測，直到MAPE達到評價指標要求，本文取為0.1，獲取最終的預測模型。

最后，對該模型進行反歸一化處理，建立風電場短期發電功率預測模型，即功率與輸入參數的回歸方程。

2）模型測試。

讀取測試數據，代入功率預測回歸模型，得到預測功率。將預測功率和實際功率進行比較，得到測試樣本各個時間點對應的功率預測相對誤差，最后計算整個測試樣本的MAPE值。該MAPE值即為風電場短期功率預測精度。

3）預測誤差修正。

風電場短期的歷史功率預測數據和實測數據的差值，形成一個新的時間序列，該時間序列與未來的基于同樣原理產生的時間序列之間存在某種映射關系，因此可以應用誤差的歷史值去預測誤差的未來值，此過程即為誤差修正過程。

基于馬爾可夫鏈對風電場功率預測的預測誤差進行修正。在預測誤差修正過程中，根據測試數據的預測相對誤差最大值與最小值，計算區間間隔，如式（10），區間數與測試樣本數相同，即

式中：Δ為區間間隔；εmax為預測相對誤差最大值；εmin為預測相對誤差最小值；n為測試樣本數量。

在此基礎上，對樣本數據的相對誤差進行區間劃分，得到預測相對誤差所處的狀態，進一步可以得到一步狀態轉移矩陣，如式（7）。最后根據前一時間誤差所處的狀態，運用最小二乘法由歷史誤差與預測誤差確定修正后的功率預測值[15-18]，建立誤差修正后的數學模型，即為預測誤差修正模型。其具體的算法流程如圖1所示

3 風電場短期功率預測

圖1 算法流程Fig.1 A lgorithMflow chart

4 算例分析

本文選取陜北某小型風電場所在地區的風速、溫度、大氣壓強及風電場發電功率作為訓練樣本。每10min取一次樣，取連續100組數據進行訓練，之后用連續的32組數據進行測試。應用Matlab軟件進行編程計算，測試樣本數據曲線如圖2～圖4所示。

圖2 風電場的風速變化Fig.2 W ind speed variation ofw ind farm

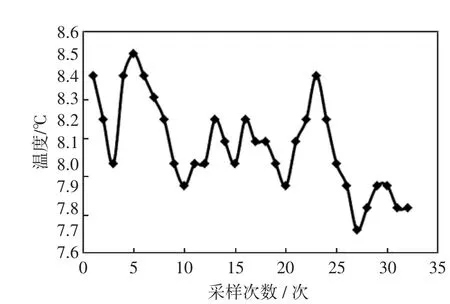
圖3 風電場的溫度變化Fig.3 Temperature variation ofw ind farm

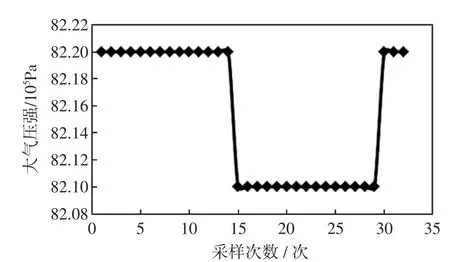
圖4 風電場的大氣壓強變化Fig.4 Atmospheric pressure changesofw ind farm

由圖2～圖4可以看出，風電場的風速、溫度、壓強都是隨機的，沒有規律性。

將樣本的輸入和輸出導入程序中。首先，基于相關向量機原理進行模型訓練和測試，得出對應時間的風功率預測值；然后，根據風功率的預測值和實際值，求出預測相對誤差序列；最后，利用馬爾可夫鏈對預測誤差進行修正。

同時，根據神經網絡和支持向量機原理，使用相同的樣本數據，進行風功率預測。

如圖5所示為風電場實際功率、幾種預測方法的預測功率以及本文方法的預測功率。由圖5可以看出，經誤差修正后，預測值和實際值之間的相關性明顯增強。

如圖6所示為各種預測方法的預測相對誤差。表1所示為幾種預測方法的平均相對誤差。可以看出，誤差修正后，預測相對誤差的平均值和最大值都明顯減小。

圖5 風電場預測輸出功率Fig.5 W ind farMs predicted output power

圖6 相對誤差Fig.6 Relativeerror

表1 預測誤差Tab.1 Prediction errors

表1中，MAE（meoMaverage absolute error）為平均絕對誤差，其計算公式為

綜上可以看出：相關向量機與馬爾可夫鏈結合的方法與其他預測方法相比，平均絕對誤差和平均相對誤差都小，預測精度較高。

另一方面，根據算例結果可以看出，預測的最大相對誤差和絕對誤差，雖然與其他方法相比較大大減小，但仍然達到13%，其原因是：①風機發電功率與風速的關系只有在額定的啟動風速和切出風速之間才滿足。低于啟動風速時，風機輸出功率為0，高于切出風速時，風機輸出功率為最大值；②原始輸入數據為3維（風速，大氣壓強，溫度因素），沒有考慮其他因素（如風向，地形條件，大氣湍流等因素）的影響。而RVM－Markov的預測方法不僅適用于輸入數據為3維的情況，也適用于輸入數據更多維數的情況。當獲取影響風功率預測多種因素輸入數據時，運用本文提出的方法，將會進一步減小風電場短期功率預測的誤差。

5 結語

本文將相關向量機原理用于風電場短期功率預測，提出了基于相關向量機—馬爾可夫鏈的風電功率預測方法。該方法首先運用相關向量機原理，得到風電場短期功率預測模型，然后應用馬爾可夫鏈和最小二乘法對誤差進行修正，建立風電場短期功率誤差修正模型，最后，將預測模型和誤差修正模型應用于實際風電場功率預測。實際算例驗證結果表明，本文提出的預測方法與其他預測方法相比較，平均相對誤差和最大相對誤差都較小，能夠滿足電力系統調度對風電場短期功率預測的要求。

[1]范高鋒，王偉勝，劉純（Fan Gaofeng，WangWeisheng，Liu chun）.基于人工神經網絡的風電功率短期預測系統（Artificial neural network based wind power short terMprediction system）[J].電網技術（Power SysteMTechnology），2008，11，32（22）：72-76.

[2]朱曉榮，劉艷萍（Zhu Xiaorong，Liu Yanping）.基于穩健估計時間序列法的風功率預測（Wind power forecasting using timeseriesmodelbased on robustestimation）[J].電力系統及其自動化學報（Proceedingsof the CSU-EPSA），2012，24（3）：107-110，126.

[3]郭鵬（Guo Peng）.殘差灰色風速預測最大風能追蹤策略研究（A new MPPT strategy based on residualerrorgray wind speed prediction）[J].太陽能學報（Acta Energiae Solaris Sinica），2011，32（4）：548-552.

[4]彭信淞，賀輝，姚建剛，等（Peng Xinsong，He Hui，Yao Jiangang，etal）.用PSO優化BP神經網絡的母線負荷預測方法（Method ofbus-load forecasting using BPneural network optimized by PSO）[J].電力系統及其自動化學報（Proceedingsof theCSU-EPSA），2010，22（5）：146-151.

[5]孟洋洋，盧繼平，孫華利，等（Meng Yangyang，Lu Jiping，Sun Huanli，etal）.基于相似日和人工神經網絡的風電功率短期預測（Short-terMwind power forecasting based on similar days and artificial neural network）[J].電網技術（Power SysteMTechnology），2010，34（12）：163-167.

[6]王奔，冷北雪，張喜梅，等（Wang Ben，Leng Beixue，Zhang Ximei，etal）.支持向量機在短期負荷預測中的應用概況（Application profiles of supportvectormachine in short-terMload forecasting）[J].電力系統及其自動化學報（Proceedingsof the CSU-EPSA），2011，23（4）：115-121.

[7]SangitaBP，Deshmukh SR.Use ofsupportvectormachine forwind speed prediction[C]//International Conference on Powerand Energy Systems，Chennai，India，2011.

[8]孫志剛，翟瑋星，李偉倫，等（Sun Zhigang，ZhaiWeixing，LiWeilun，etal）.基于EMD和相關向量機的短期負荷預測（Short-terMload forecasting based on EMD and vector machine）[J].電力系統及其自動化學報（Proceedingsof the CSU-EPSA），2011，23（1）：92-97.

[9]黃帥棟，衛志農，高宗和，等（Huang Shuaidong，Wei Zhinong，Gao Zhonghe，etal）.基于非負矩陣分解的相關向量機短期負荷預測模型（A short-terMload forecasting model based on relevance vectormashine with nonnegativematrix factorization）[J].電力系統自動化（Automation ofElectric Power Systems），2012，36（11）：62-66.

[10]夏君常，謝開貴，曹侃，等（Xia Junchang，Xie Kaigui，Cao Kan，etal）.電力市場短期電價預測的誤差修正模型（Error correction model for short-terMelectricity price forecasting）[J].華東電力（East China Electric Power），2011，39（2）：161-167.

[11]朱永強，田軍（Zhu Yongqiang，Tian Jun）.最小二乘支持向量機在光伏功率預測中的應用（Application of least square supportvectormachine in photovoltaic power forecasting）[J].電網技術（Power SysteMTechnology），2011，35（7）：54-59.

[12]孟巖峰，胡書舉，鄧雅，等（Meng Yanfeng，Hu Shuju，Deng Ya，etal）.風電功率預測誤差分析及預測誤差評價方法（Analysisand evaluationmethod ofwind predictederror）[J].電力建設（Electric PowerConstruction），2013，34（7）：6-9.

[13]丁志勇，楊蘋，楊曦，等（Ding Zhiyong，Yang Ping，Yang Xi，etal）.基于連續時間段聚類的支持向量機風電功率預測方法（Wind power predictionmethod based on sequential time clustering support vectormachine）[J].電力系統自動化（AutomationofElectric PowerSystems），2012，36（14）：131-135，149.

[14]Huang ShianChang，Wu TungKuang.Wavelet-based relevance vectormachines for stock index forecasting[C]//International Joint Conference on Neural Networks，Vancouver，Canada，2006：603-609.

[15]Niu Lin，Liu Min，Zhao Jianguo，et al.Prediction of audible noise froMUHV AC transmission lines based on relevance vector learningmechanism[C]//Asia-Pacific Power and Energy Engineering Conference.Chengdu，China，2010.

[16]黃銀華，彭建春，李常春，等（Huang Yinhua，Peng Jianchun，LiChangchun，etal）.馬爾可夫理論在中長期負荷預測中的應用（Application ofMarkov theory inmidlong terMload forecasting）[J].電力系統及其自動化學報（Proceedingsof the CSU-EPSA），2011，23（5）：131-136.

[17]丁明，徐寧舟（Ding Ming，Xu Ningzhou）.基于馬爾可夫鏈的光伏發電系統輸出功率短期預測方法（Amethod to forecastshort-terMoutputpower of photovoltaic generation systeMbased on Markov chain）[J].電網技術（Power SysteMTechnology），2011，35（1）：152-157.

Short-terMW ind FarMPower Prediction

YANGXiaoping，WANGBao，LANHang，WUXiaoxuan
（Faculty ofWater Resourcesand Hydraulic Power，Xi′an University of Technology，Xi′an 710048，China）

The prediction of thewind power output iswith greatsignificance for the power systeMoperation which is interconnected to a large numberofwind power.In this paper，based on the problemsof conventionalpredictionmethods-prediction accuracy is not sufficient，in order to solve this，a novel short-terMpower forecastingmethods-Relevance vectormachine-Markov chain is proposed.With the utilization of the principle of relevance vectormachine，the original predictionmodel is builtup.Then，the error is corrected with Markov chain principle，the short-terMpower forecasting-error correctionmodelofwind farms is constructed by the leastsquaresmethod.Themethod is used for the actualshort-terMwind farMpower prediction，itsaverage relative error is7.2%.The resultsof this forecast indicate that the proposedmethod canmeet the requirements of the power systeMscheduling in short-terMwind farMpower prediction.

wind farm；short-terMpower；prediction；relevance vectormachine；markov chain

TK81

A

1003-8930（2015）09-0085-06

10.3969/j.issn.1003-8930.2015.09.15

楊曉萍（1963—），女，博士，教授，從事電力系統運行與控制和電力電子在電力系統中的應用研究。Email：yangxiaoping @xaut.edu.cn

2013-12-24；

2014-04-16

王寶（1988—），男，碩士研究生，從事電能質量與柔性輸電技術的研究。Email：296485450@qq.com

蘭航（1989—），男，碩士研究生，從事電力系統及其自動化的研究。Email：478129614@qq.com