基于Harris 算子的灰度圖像角點檢測方法研究

□趙 慧

隨著計算機應用的發展，數字圖像處理在人們的生活中有了很廣泛的應用。角點是圖像的重要特征，它是圖像灰度局部曲率的極大點，決定了對目標輪廓特征的掌握程度。角點在各種影像特征中有很多優點，例如旋轉不變性、不隨光照變化而變化等。在圖像匹配中，角點也發揮著很大的作用，利用角點特征可以大大提高圖像匹配的速度。另外，角點還可以作為輸入，用于3D 目標跟蹤、3D 建模等領域。由于角點檢測的廣泛應用，角點檢測的研究己成為很多課題的重要環節［1］。本文利用Harris 算法對灰度圖像提取角點，并定性比較了基本的Harris 角點檢測算法和在此基礎上改進的基于散布矩陣的Harris 角點檢測算法的性能。

一、Harris 角點檢測算子原理

角點是灰度變化足夠大的點，人眼對角點的識別通常是在一個小窗口內完成的。當一個窗口在圖像上移動時，窗口內灰度在各個方向上都沒有發生變化，則它在平坦區域，如圖1(a)所示;如果窗口沿某一方向上移動，窗口內灰度發生了較大的變化，而沿另一方向移動，窗口內灰度沒有發生變化，則它有可能在邊緣區域，如圖1(b)所示;如果窗口沿任意方向移動時，窗口內灰度發生明顯的變化，則認為在窗口內遇到了角點，如圖1(c)所示。Harris 算子就是通過這一物理現象，來判斷角點的［2］。

圖1 窗口的移動與角點檢測

將圖像窗口平移［u，v］產生灰度變化E(u，v):

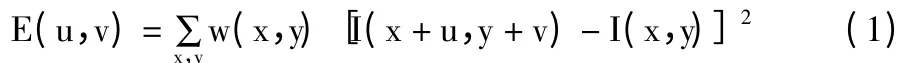
其中w(x，y)是窗口函數，是原像素點的灰度，是平移后像素點的灰度。

根據泰勒公式展開，上式可近似寫為:

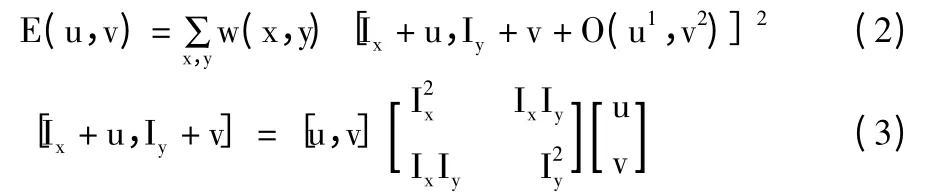
于是對于局部微小的移動量［u，v］，可以近似得到下面的表達:

其中實對稱矩陣M 的可表示為:

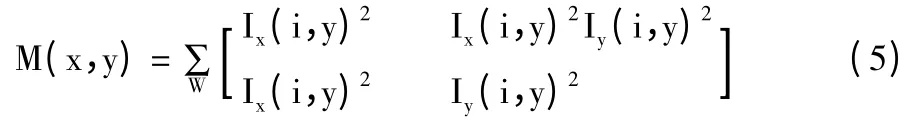
其中Ix、Iy 分別是I 沿x 和y 方向的一階導數。

圖像灰度的自相關函數在某一點處的曲率極值可用矩陣的特征值λ1、λ2表示。一是兩個特征值都很小且近似相等，即λ1≈λ2≈0，則證明在各個方向上的自相關函數都很小，檢測為平坦區域。二是兩個特征值都很大且近似相等，即λ1≈λ2≥0，則證明在所有方向上的自相關函數都很大，檢測為角點。三是兩個特征值中一個大，一個小，即λ1≥λ2或λ1≤λ2，即自相關函數在某一方向上大，在其他方向上小，則檢測為邊緣。

由于Harris 角點檢測中需要計算圖像灰度的梯度，所以Harris 角點檢測受噪聲影響嚴重，檢測出的角點效果不好。因此，有人提出了基于散布矩陣的角點檢測方法。

散布矩陣的定義如下:

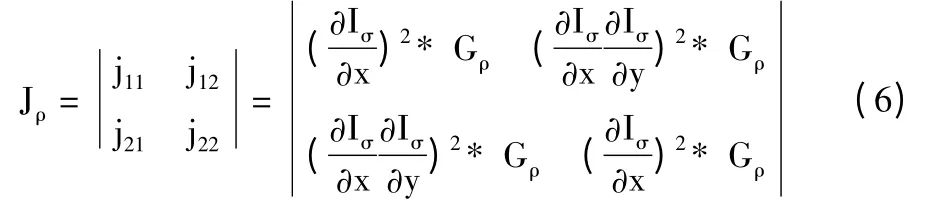
式中Iσ表示以σ 為平滑參數的Gaussian 平滑圖像，Gρ表示以ρ 為參數的Gaussian 核。

矩陣Jρ有兩個特征向量，它們的方向矢量分別是:

其中代表圖像的梯度方向，即垂直圖像特征的方向;代表沿圖像特征的方向，也就是圖像邊緣的切線方向;是與水平軸的夾角。

由于散布矩陣在對圖像I 求微分前后兩次采取了高斯平滑的手段，通過考慮局部鄰域增強結構方向估計的魯棒性，因而可以有效屏蔽噪聲對角點檢測的影響。邵文澤［3］基于散布矩陣提出了一個角點檢測算子:

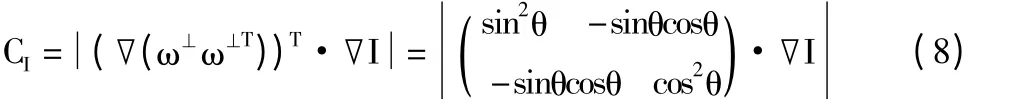
其中

因而可以根據散布矩陣，得出(7)和(8)中

二、實驗結果及討論

在無噪、高斯模糊和有高斯噪聲三種情形下，對基于散布矩陣的Harris 角點求取方法進行了實驗，實驗結果如圖2所示。這里沒有對檢測的角點強度圖進行二值化，只給出了角點強度的灰度圖，圖中灰度值越高的點表示此處的角形結構越強。從實驗結果可以看出，由于散布矩陣根據圖像的局部鄰域結構特征識別和確定角形結構，因此該方法的抗噪性好，求取的角點穩定。

圖2 Harris 算子角點檢測的抗噪性測試結果

三、結語

角點是重要的圖像特征點，角點檢測在各種圖像處理技術中被廣泛應用。本文研究了基本的Harris 角點檢測算法，以及在此基礎上改進的基于散布矩陣的Harris 角點檢測算法。實驗結果表明，基于散布矩陣的Harris 角點檢測算子穩定性更高，抗干擾性強，魯棒性更好。

［1］王玉珠.圖像角點檢測算法研究［D］.重慶大學，2007

［2］胡俊.圖像角點檢測方法的研究［D］.重慶郵電大學，2011

［3］邵文澤.基于圖像建模理論的多幅圖像正則化超分辨率重建算法研究［D］.南京理工大學，2008