基于非限制MIDAS模型的GDP增長研究

□柏久麟

宏觀經濟中有許多能反映當前宏觀經濟狀態和未來宏觀經濟走勢的經濟數據，如季度GDP數據、月度CPI和PPI數據等。這些數據受到經濟個體、企業、組織和國家，國際社會的廣泛關注，人們使用不同的數據處理方法和構建各種模型從這些紛繁復雜的數據中提取信息，以便能夠得出當期宏觀經濟的準確預報和未來一段時間內宏觀經濟走勢的精確預測。然而，在構建宏觀經濟模型時卻由于種種原因經常出現數據抽樣的頻率高低有別的問題，而大多數宏觀經濟模型都要求模型等式兩邊的數據頻率是一致的，因此要想利用傳統宏觀經濟模型去估計、預報和預測宏觀經濟的話就必須對混頻數據進行處理。

最初，國內外對于混合頻率數據的處理方法是將高頻數據處理為低頻數據(Silvestrini和Veredas，2008)，而其他的則是采用插值法將低頻數據處理為高頻數據(Chow和Lin，1971、1976;趙進文和薛艷，2009)。但是這兩種處理方法有著顯而易見的缺陷，將高頻數據處理為低頻數據處理過程中忽視了高頻數據中部分樣本信息，抹殺了高頻數據的波動，在一定程度上人為地減少了樣本信息，但是由于該方法使用上較為簡單，所以在實際應用中這種方法較為流行;而插值法在應用上相對較少，但對該方法的研究卻相當多。雖然插值法能獲得高頻數據，但是這種高頻數據存在著明顯的人造數據的嫌疑，其結果的真實性往往值得懷疑，這也是該方法在實際應用中使用較少的重要原因。

混頻數據模型的理論優勢在于不對混頻數據做任何處理，而是利用原始數據的信息構建數據模型。當前處理混頻數據的模型主要有以下兩種:混合頻率數據抽樣(MIDAS，MIxedDAta Sampling)模型和混合頻率向量自回歸(MFVAR)模型。MIDAS模型是Ghysels等人(Ghysels，Santa-Clara和Valkanov，2004)在分布滯后模型的基礎上提出來的混合頻率數據抽樣。Clements、Galv~ao(2005)開始將MIDAS模型應用于宏觀經濟領域的理論研究，Marcellino、Schumacher(2007)將因子模型引入到MIDAS模型，模型的預測結果顯示MIDAS模型在短期預測中表現較為優秀，且非限制的U-MIDAS模型在很多實際預測中具有最佳的預測效果。

一、MIDAS回歸模型以及U-MIDAS回歸模型

(一)MIDAS模型。單變量的MIDAS模型是由Ghysel(2004)等基于分布滯后模型提出的，此模型最初提出時，運用了一個參數化的權重多項式，直接利用高頻數據與低頻數據構建模型，此模型的估計方法一般為非線性的最小二乘法進行估計。

單變量MIDAS回歸模型如下:

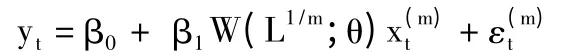
其中，yt是低頻因變量變量是高頻自變量。m代表高頻數據和低頻數據之間的倍率。如果yt是季度數據是月度數據，那么m=3。W(L1/m;θ)為滯后權重多項式，相應表達式如下為高頻滯后算子，我們有。其中，K為滯后權重多項式的階數。

當K=3時，MIDAS模型可以攜程如下形式

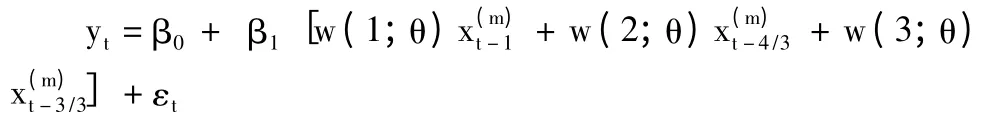
一般來說MIDAS模型最為常用的滯后權重多項式為指數Almon滯后多項式。基由次權重多項式可以構建出多種不同的權重多項式。一般來說，宏觀經濟學中常用兩參數的Almon指數多項式，并且限定θ1≤300，θ2＜0的條件。如此，即可得到滿足一般宏觀經濟預測所需要的權重形式。(Clements，2008)

(二)U-MIDAS模型。在一般情況下，我們可以看到，MIDAS模型在估計之前都要對滯后權重多項式進行限定。是在某些情況下，我們會發現，對于事前假定滯后權重多項式的設定常常是不客觀的。基于這種情況，Foroni，Marcellino，and Schumacher(2011)對原始的MIDAS模型進行改進。取消了模型中的滯后權重多項式的限定。這樣的模型被稱為非限定的MIDAS模型，即U-MIDAS模型。

一般來說，U-MIDAS模型的具體形式如下:

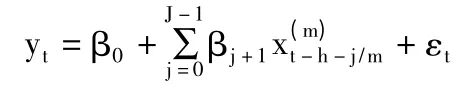
其中J為回歸模型中解釋變量的滯后階數。模型中的其余的參數均與一般的MIDAS模型一致。

二、實證分析

本文將采用2000年1季度至2013年4季度的GDP同比增長率yt，月度固定次產投資的同比增長率，月度社會消費品零售總額同比增長率，以及月度出口總額的同比增長率分別構建MIDAS模型以及非限制性MIDAS模型。

對于模型的檢驗主要有兩個方面，第一是模型在樣本內的擬合精度，通常的衡量標準為擬合優度。第二是模型在樣本外的預測精度，通常衡量的方法是建立損失函數。在預測模型時，建立不同的損失函數就會衍生出不同的預測結果。本文將用比較常見的誤差均方根(RMSE)來評價模型的預測精度。本文的模型預測與檢驗均采用matlab進行編程。

我們用以上GDP，月度固定次產投資，月度社會消費品零售總額，月度社會消費品零售總額分別采用MIDAS模型與U-MIDAS模型進行模擬。對于我國的國情來講，通常來說，一個完整的經濟周期為12個月。這里我們可以先行假設模型的滯后權重為12。在模擬MIDAS模型時，我們所采用的滯后權重多項式為最常用的Almon滯后多項式。

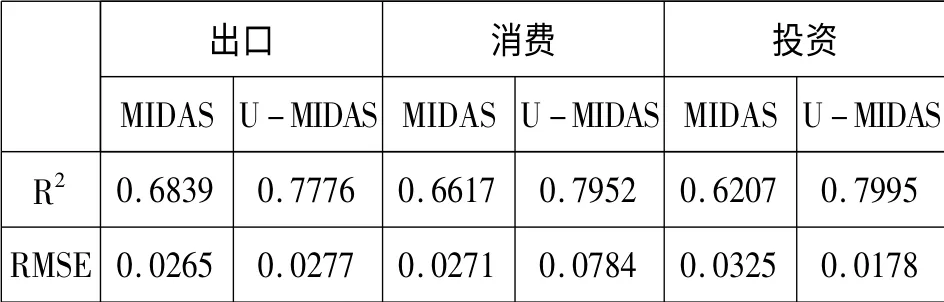
表1 MIDAS模型與U-MIDAS模型估計結果

由表1我們可以看出，在擬合優度方面，U-MIDAS模型全面優于一般的MIDAS模型。這里可以看出，由于去掉了滯后權重多項式的限制，使得非限制性的MIDAS模型具有了更高的靈活性，使得擬合精度大大提高。

另一方面，在預測精度上面，出口與消費部分U-MIDAS模型則預測效果不佳。調整了相關的滯后權重后我們得到了出口與消費的誤差均方根表。

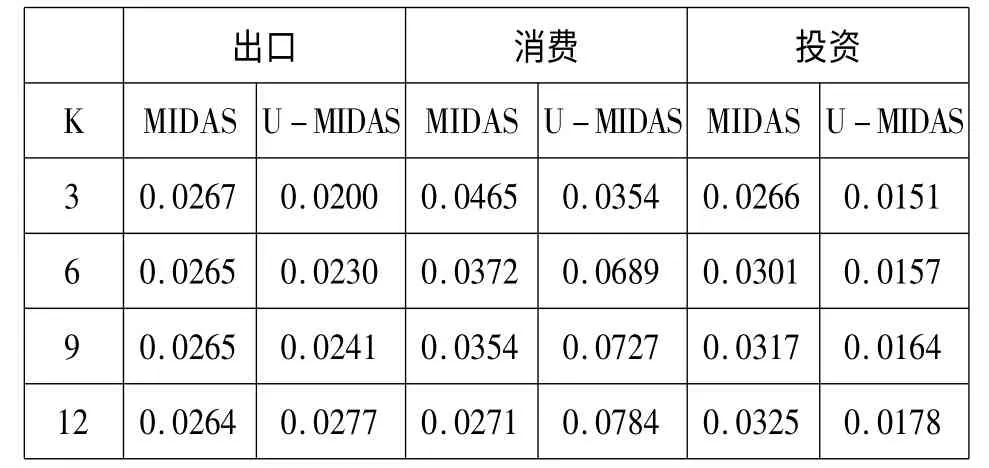
表2 不同滯后階數下三個因子的RMSE變化

三、模型預測結果與評價

經過上面的擬合結果分析可以得到如下三點結論:第一，由于U-MIDAS模型取消了滯后權重多項式限定時的模型的靈活度大大提升，這使得模型的擬合精度相對于一般MIDAS模型具有明顯優勢。第二，U-MIDAS模型由于取消了滯后權重多項式的限定，隨著滯后階數的增加——這直接導致模型需要估計的參數大量增加——模型的穩定性迅速下降。這是在使用U-MIDAS模型進行預測時值得注意的問題。第三，就我們研究的這個問題看來。消費，出口，投資對于GDP有著不同的影響力，我們可以看到，中國GDP的波動與出口的波動最為相關。這也是中國作為一個出口為主的國家的基本國情決定的。

［1］Andreou，E.，Ghysels E.，and A.Kourtellos，2010，Regression models with mixed sampling frequencies［J］.Journal of Econometrics，doi:10.1016/j.jeconom，2010，1:4

［2］Clements，M.P.，and A.B.Galvo，2005，Macroeconomic forecasting with mixed-frequency data:Forecasting US output growth administration，Warwick working paper

［3］Ghysels，E.，A.Sinko，and R.Valkanov.MIDAS regressions:Further results and new directions［J］.Econometric Reviews，2007，26(1):53～90

［4］Ghysels，E.，Santa-Clara，P.and R.Valkanov.The MIDAS touch:Mixed data sampling regressions［J］.mimeo，Chapel Hill，N.C，2004

［5］Marcellino，M.，andC.Schumacher，Factor nowcasting of German GDP with ragged-edge data.A model comparison using MIDAS projections，Bundesbank Discussion Paper，2004，1(34)

［6］VladimirKuzin，MassimilianoMarcellino，Christian Schumacher.MIDAS versus mixed-frequency VAR:nowcasting GDP in the euro area［J］.International Journal of Forecasting，2011，2(27):529～542

［7］劉漢.中國宏觀經濟混頻數據模型的應用與研究［D］.吉林大學，2013

［8］陳浩東.基于混頻數據模型對通貨膨脹與經濟增長影響的實證研究［D］.吉林大學，2012

［9］劉金全，劉漢，印重.中國宏觀經濟混頻數據模型應用［J］.經濟科學，2010

［10］耿鵬，齊紅倩.我國季度GDP實時數據預測與評價［J］.統計研究，2012

［11］趙進文，薛艷.我國分季度GDP估算方法的研究［J］.統計研究，2009

［12］龔玉婷，陳強，鄭旭.基于混頻模型的CPI短期預測研究［J］.統計研究，2014