按“四基”的要求編寫數學教材

張奠宙

隨著時代的進步，一些現代數學內容，逐漸進入了小學數學課程。在六年級的小學數學教材里，出現了組合數學中常用的“抽屜原理”。這是一個與時俱進的數學教學改革成果，值得肯定。但是，在如何呈現這類新內容的途徑上，可以有更多的不同選擇。《義務教育數學課程標準（2011年版）》突出地強調“四基”教學，即注重基本數學知識、基本數學技能、基本數學思想方法、基本數學活動經驗的教學。按照這一要求，抽屜原理的教學如何設計，教材上如何表述，值得研究。

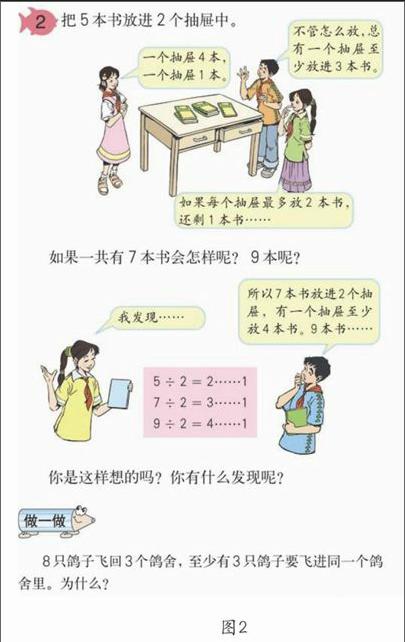
首先，在某教材六年級“數學廣角”單元的第一頁（圖1），直接出示“文具盒放鉛筆”的問題，沒有用“抽屜原理”作為標題，令人遺憾。事實上，抽屜原理，或者鴿籠原理，乃是一種邏輯推理方法。它是一種普適的原理，并非單純的個別數學問題。時至今日，它們已經成為了國際通用的名詞，業已成為人們的常識。不出現“原理”二字，就將它弱化了。

其次，要研究抽屜原理教材所應表述的重點所在：究竟是當作一種“知識”進行展示呢，還是突出數學思想方法加以呈現呢？

按照現在的處理（見圖1），仍然將它當作一種解題知識加以表述。思考的順序是：

提出放鉛筆問題 直接給出答案 用窮舉法加以證明，最后總結為“還可以這樣想……”

這里，只是把抽屜原理當作一個“問題解決”的個別例題進行呈現，因而馬上給出答案。最不妥的是把窮舉各種情況作為論證的基礎。然而，抽屜原理并不是靠窮舉各種情況再加以歸納出來的。恰恰相反，學習抽屜原理的意義在于丟開窮舉檢驗，訴諸邏輯論證。

圖1

現在，我們不妨將上述教材的呈現順序反過來，按照“四基“的要求進行教材設計。

標題：抽屜原理

●把4個蘋果放到3個抽屜里，會不會有一個抽屜里至少有2個蘋果呢？

●小胖說：“我來放放看。”

●小明說：“不必一個個地放蘋果，我也能斷定，總有某一個抽屜里至少有2個蘋果。”

●為什么呢？

●因為蘋果比抽屜多一個。如果每一個抽屜里都只放1個蘋果，最多放3個。那么一定多出來1個蘋果。現在還要把它放到某一個抽屜里去，那么那一個抽屜就會有2個蘋果了。

●小胖說：“是的，我把各種情況都擺出來了。小明的判斷是對的。”

●歸納：把N個蘋果放到M個抽屜里（N>M），那么一定存在某一個抽屜中至少有2個蘋果。

以上的設計，突出原理的普適性，彰顯邏輯推理數學方法的理性價值。

接下來，還可以進行以下的數學活動。

標題：數學活動

活動1：現在有102個蘋果，要放到100個抽屜里，試問是不是一定在某個抽屜里有2個以上的蘋果？來得及把所有情況都擺出來嗎？怎樣論證你的結論？你知道是哪一個抽屜里的蘋果數大于2嗎？能不能肯定該抽屜里恰好有2個蘋果？

活動2：某學校有400名學生，問是否會有兩個學生同一天過生日？

（分組討論，匯報總結）[ 這是教材里的一個練習， 不妨作為課堂活動讓學生討論研究。]

這是一項非常重要的基本數學活動。事實上，活動1呈現的情況可以是成千上萬的，根本無法擺完全，但是，運用抽象的演繹推理可以得出絕對肯定的結論。后面兩個問題，是要說明抽屜原理是純粹的存在性定理，只知其中有一個抽屜里至少有2個蘋果，卻不知道究竟是哪一個抽屜。也只知道某抽屜里的蘋果數至少是2，卻不能肯定究竟是幾個？也許102 個蘋果都放在某一個抽屜里呢！活動2是一個看起來無法回答的問題，卻給出了絕對正確的答案。理性的力量令人震撼。積累這樣的數學活動經驗，并將之內化為一種數學思想方法，學生將終身受用。

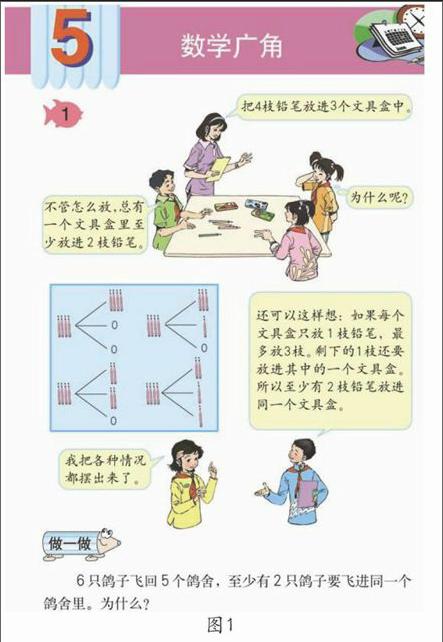
某教材的第二頁，出現了5本書放到兩個抽屜的情形（圖2），并引申到了7本、9本的情形。這是否有必要？放入練習如何？遺憾的是，教材呈現的情形越來越復雜，卻沒有展現每章蘊含的數學思想方法，制作極端情形。雖然教材的內容不可能包羅萬象、面面俱到，但也不能把落實“四基”的任務統統推給任課教師。教材應該首先垂范才是。

圖2

以下讓我們來進行一些現代數學的注釋，也許可以寫入教學參考資料，供教學參考。

1.關于數學中的存在性定理和構造性定理

數學中有許多存在性的命題。它能肯定一些對象的存在，卻不能具體地構造出來。最著名的是高斯首先證明的代數基本定理：在復數域內，任意單變元的N次代數方程，必有N 個根。但定理只是斷言根的存在，卻沒有指出具體的根是什么。另一種問題則不同，比如雞兔同籠這樣的命題，不僅知道此問題一定有解，而且按照一定的方法，可以把解具體地求出來，即“構造”出來。這一類命題稱為構造性的命題。中國古代數學，擅長構造性數學，善于用機械化的算法，將問題的解構造性地算出來。

2. 關于存在性數學命題的人文意境

存在性定理最美麗動人的描述，可以在中國古典詩詞中獲得。小學語文教材里收有賈島的詩作《尋隱者不遇》，其中寫道：

松下問童子，言師采藥去。

只在此山中 云深不知處。

詩句肯定藥師必定在山中，但是云深不知處。如果我們的教材里，引用這首小詩，是不是有助于對存在性命題的理解呢？是否有助于中華文化和西方數學的融合呢？教材能不能有一點創新呢？

3.初步接觸邏輯量詞

20世紀以來，數理邏輯迅猛發展。其中使用了兩個邏輯量詞，對數學教學的影響巨大。它們是：全稱量詞“任意一個”（傳統符號是，它倒過來的字母是 A），表示單詞 “all（每一個）”;存在量詞的相應的符號是 ，它是反過來的字母 E，表示單詞“exists（存在一個）”。抽屜原理要用到存在量詞 。教材里有“總有一個“的詞語，其實就是說“存在某一個”抽屜如何如何。為了傳達量詞的真意，和后續課程接軌，建議多用“存在某一個”的說法。存在量詞的否定形式就是“全稱量詞”。事實上，“不存在某一個……”就意味著“任意一個都不……”這在中學數學和高等數學里使用非常頻繁。

（華東師范大學數學系 200241）endprint