帶移動滑塊太陽帆航天器姿態控制技術研究及仿真

張震亞，韓艷鏵，賈 杰

（1.南京航空航天大學 航天學院，江蘇 南京 210016；2.南昌航空大學 信息工程學院，江西 南昌 330063）

0 引言

太陽帆作為一種全新航天器推進機構，由于無需消耗任何化學燃料和能源即可在太陽光壓持續推進下實現高速飛行，成為近年來航天領域的研究熱點［1］。因裝配誤差及帆面變形等因素，太陽帆光壓壓心往往不與系統質心重合，光壓會對太陽帆產生遠大于傳統航天器的姿態干擾力矩［2］。同時由于太陽帆結構尺寸龐大，其三軸轉動慣量遠超過普通航天器（美國ATK研制的160m級，440kg方形太陽帆航天器的滾轉軸慣量達642 876kg·m2，俯仰軸和偏航軸慣量均為321 490kg·m2［3］。），若采用飛輪或反作用噴嘴等傳統執行機構對其姿態進行控制，則需消耗大量能源或工質。因此必須設計新型高效率、無工質消耗的姿控系統，常用方法是利用轉動控制桿或沿帆面結構桿滑動的質量塊等機構，使太陽帆的質心相對壓心位置產生可控偏距，獲得光壓姿態控制力矩［4－6］。

與采用控制桿或控制翼面的姿態控制方案相比，基于移動滑塊的太陽帆姿態控制方案可保證有效載荷與帆面相對位置固定，利于實現天體定向觀測和對地穩定通信，且執行機構的物理結構簡單，可靠性高，輸出控制力矩較大，能滿足太陽帆大角度快速機動的姿態控制需求［7］。為此，本文對基于移動滑塊的太陽帆航天器姿態控制方案進行了研究。

1 系統動力學建模

帶移動滑塊的太陽帆航天器結構如圖1所示。其姿態控制基本原理為：在太陽帆航天器的4根結構桿上裝載可沿桿作受控滑動的質量塊，理想初始狀態下太陽帆質心與太陽光壓壓心重合，此時太陽光壓對航天器無力矩作用；通過調整滑塊位置可改變系統質心位置，使系統質心與光壓壓心間產生可控偏距，形成所需光壓姿態控制力矩。

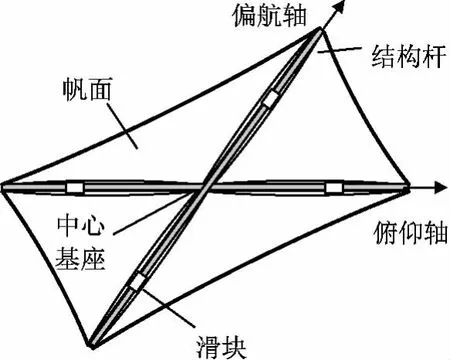
圖1 太陽帆航天器物理結構Fig.1 Structure of solar sail spacecraft

為簡化模型推導過程，建模階段將沿同對角線兩根結構桿滑動的雙滑塊等效為可沿全對角線移動的單滑塊。

1.1 坐標系和符號定義

慣性坐標系O-XY：原點O為空間某一固定點；OY軸正向與太陽光單位矢量S相反；OX軸正向與垂直太陽光單位矢量S⊥方向相同。

與太陽帆航天器固連的體坐標系Os－XsYs：原點Os為太陽帆本體質心；OsYs、OsXs軸分別指向太陽帆帆面法向與切向方向，如圖2所示。

定義太陽帆本體（含中心基座和結構桿）質量為ms，本體偏航轉動慣量為Js；移動滑塊質量為mp，視其為質點；滑塊初始時刻靜止在本體質心Os處，在方向沿結構桿的電機驅動力f作用下作可控滑動，滑塊沿導軌位移為l，忽略滑塊與導軌接觸面間的摩擦力；帆面法向與OY軸夾角為偏航姿態角α。因太陽帆制造裝配誤差和帆面變形等因素，太陽帆光壓壓心Op與本體質心Os并不重合，質心與壓心間存在偏差小量d。

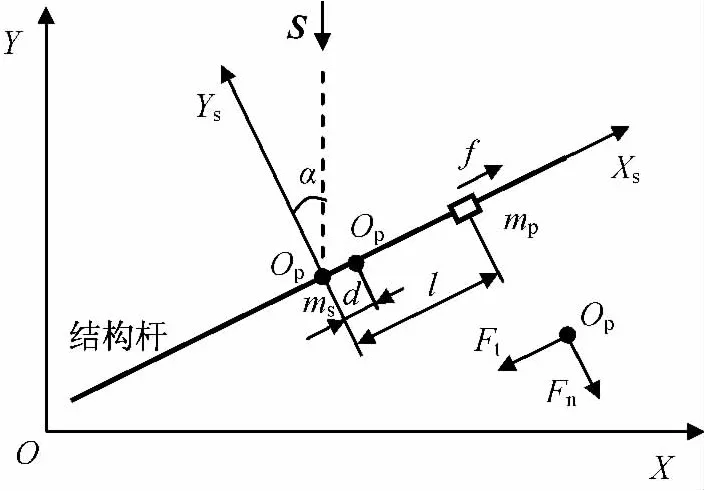
圖2 太陽帆航天器偏航軸簡化結構Fig.2 Yaw-axis simplified structure of solar sail spacecraft

1.2 太陽光壓模型

太陽光壓模型可表示為

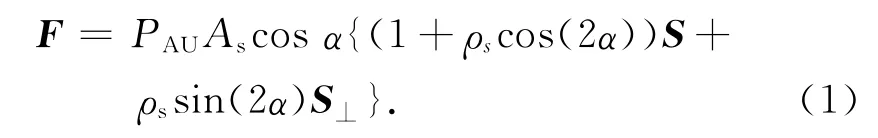
式中：PAU為距離太陽1個天文單位處光壓壓強；As為帆面面積；ρs為太陽帆鏡面反射系數［2］。定義Fs，F⊥分別為光壓力沿S和S⊥方向的分量，則有

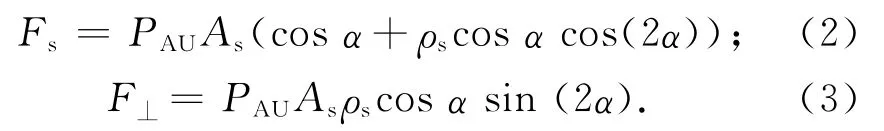
將光壓力沿帆面切向和法向進行分解（如圖2所示），并考慮帆面光學和熱力學特性，可得光壓力沿帆面切向和法向分量分別為

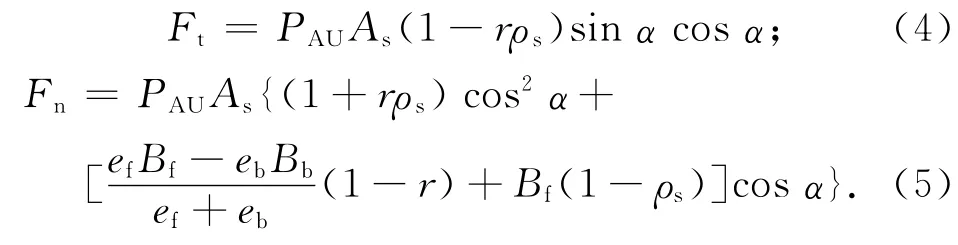
式中：Bf，Bb分別為太陽帆正面和背面的非朗伯系數；ef，eb分別為太陽帆正面和背面的發射系數；r為太陽帆正面反射率［2］。

1.3 動力學模型推導

在O-XY系中，定義太陽帆本體質心位置矢量rs＝ ［XY］T，則 滑 塊 位 置 矢 量rp＝［X＋lcosαY＋lsinα］T。設太陽帆本體動能為Ts，滑塊動能為Tp，則有

令航天器系統總動能為T，有T＝Ts＋Tp。忽略太陽帆彈性形變，則系統勢能U＝0。

定義廣義坐標q＝［αlXY］T，廣義力Q＝［Q1Q2Q3Q4］T，由虛功原理，可求得廣義力表達式為

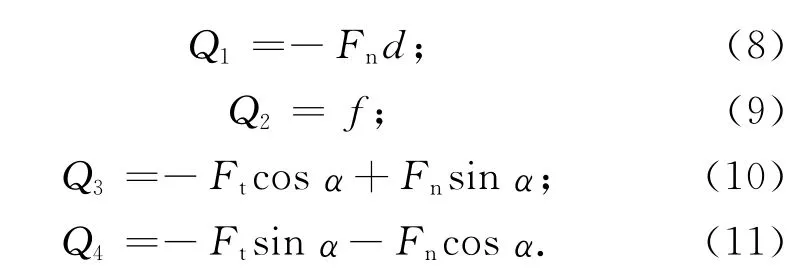
將q，Q及拉格朗日函數L＝T－U代入拉格朗日動力學方程

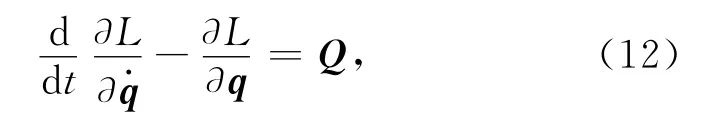
可得太陽帆航天器－滑塊兩體系統耦合動力學模型為

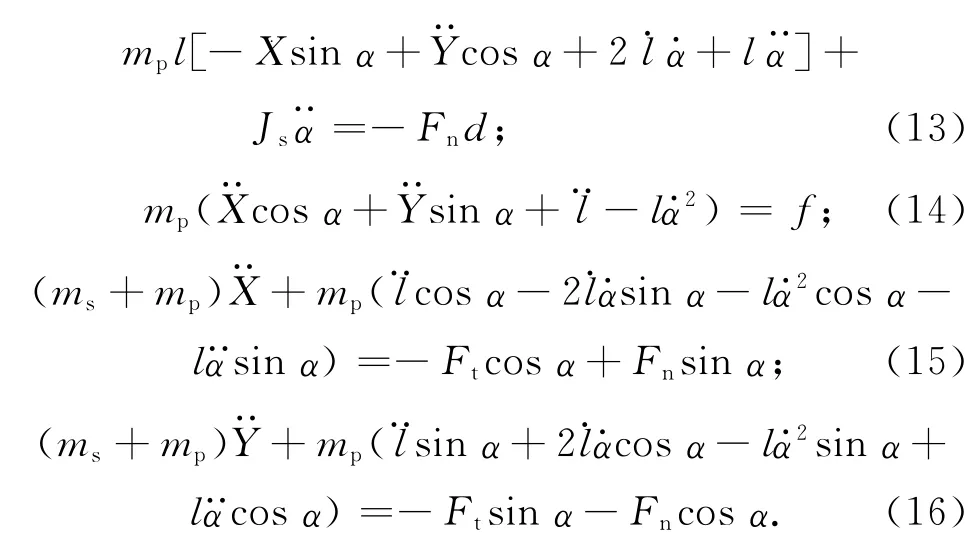
由式（13）～（16）消去變量X，Y，代入光壓模型式（4）～（5），并定義常參數

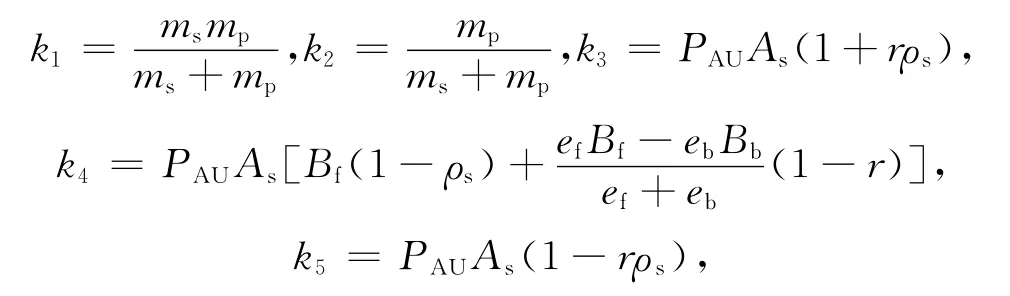
則可得太陽帆航天器偏航通道姿態動力學方程為

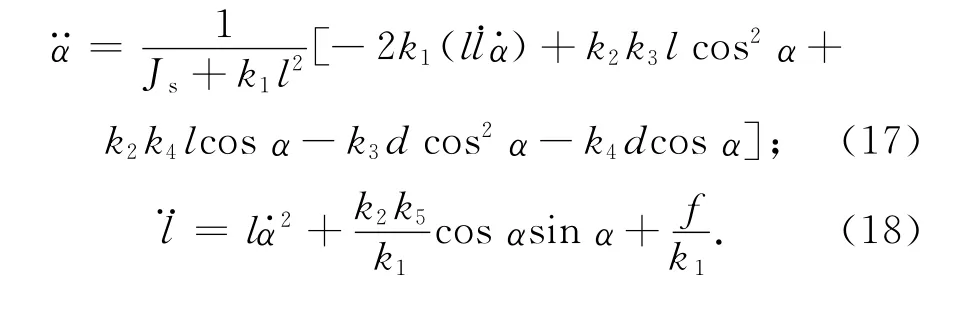
2 姿態控制器設計

對上述太陽帆航天器非線性耦合系統，若直接將滑塊驅動力作為輸入量控制航天器姿態角，則控制律的設計較難，難以在后續環節設計執行機構的分配策略；若將控制系統分為內外環回路，外環以航天器姿態為受控變量，滑塊位移為控制輸入，而內環以滑塊位移為受控變量，滑塊驅動力為控制輸入，則可顯著降低系統控制律設計的復雜度。控制系統方案如圖3所示。

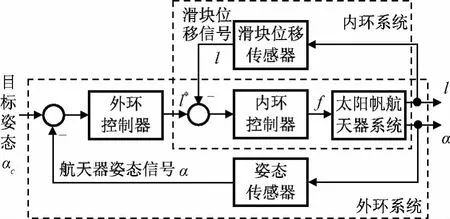
圖3 太陽帆航天器姿態控制系統Fig.3 Attitude control system of solar sail spacecraft

2.1 外環姿態控制器設計

對外環系統進行研究時，將滑塊位移l視為控制輸入，忽略l動態對航天器姿態的影響，則由式（17）可得外環系統動力學方程

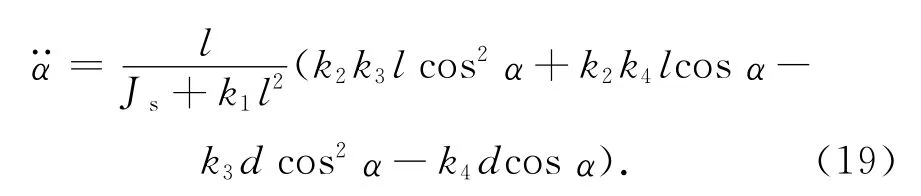
對該外環系統模型，若采用傳統的非線性系統控制律設計，僅將系統在平衡點處進行小擾動線性化，所得線性模型較原系統而言會丟失大量信息。當航天器姿態遠離系統平衡點位置時，可能導致所設計控制律的控制效果急劇下降，難以滿足實際任務中大角度姿態機動的需求。本文通過設計變增益LQR控制器以克服上述缺點，實現大范圍高精度的太陽帆航天器姿態控制。

變增益LQR控制器為一種基于增益調度的狀態反饋控制器，其基本原理是將原非線性系統在一系列狀態特征點上轉化為線性定常系統，離線求得各特征點處的狀態反饋矩陣；在線控制時用加權算法得到實時變化的系統狀態反饋矩陣，實現較精確的控制效果。

定義系統狀態變量x［］T，等效輸入控制量u，將航天器姿態角控制范圍（－90°，90°）以步長h（本文取h＝10°）劃分為p個區間，其中第q個區間兩端點為第q個和q＋1個特征點（1≤q≤p），定義第q個特征點處狀態，將系統（19）在處小擾動線性化，得特征點處線性系統模型

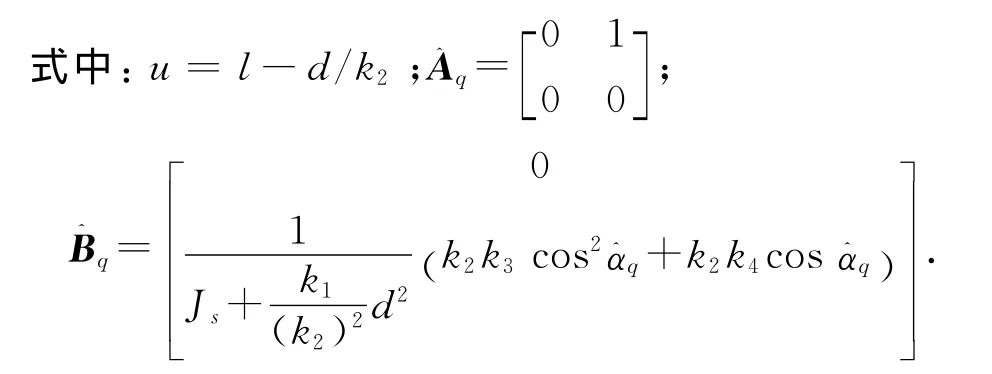
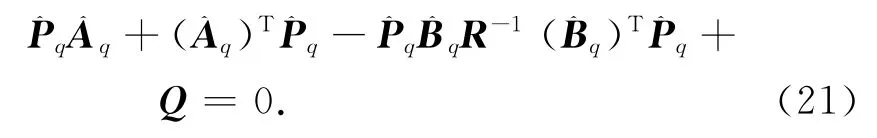
事先離線求得各特征點處狀態反饋矩陣，實際在線姿態控制時，通過實時判別當前姿態角α所屬區間q，采用加權算法

即得任意姿態角對應的狀態反饋矩陣。此處：rq為加權系數，且rq＝ ［（－90°＋q·h）－α］／h。最終求得最優控制輸入

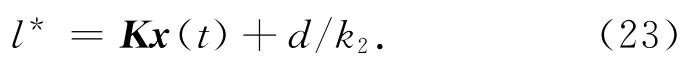
由于太陽帆結構桿長度限制，滑塊沿導軌運動區域需限制在一定范圍內。定義滑塊位移絕對值最大值為lmax，限幅處理后滑塊最優位移為，設計滑塊位移限幅器為

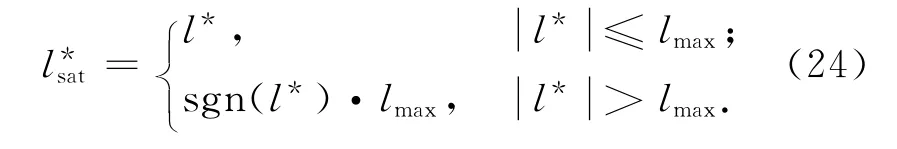
2.2 內環姿態控制器設計

內環回路以外環控制器給出的滑塊最優控制位移作為跟蹤指令，滑塊實際位移l作為受控變量，驅動力f作為控制輸入，內環動力學方程為式（18）。定義跟蹤指令位移為lc，跟蹤誤差Δll－lc，構建滑塊位置誤差Δl的理想動態為：

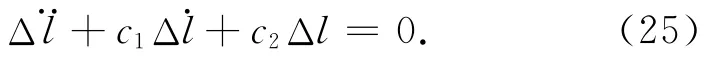
對式（25）配置合適的控制參數c1，c2，可使滑塊位置誤差Δl→0，即l→lc。將Δl＝l－lc代入式（25），聯立式（18），整理后可得

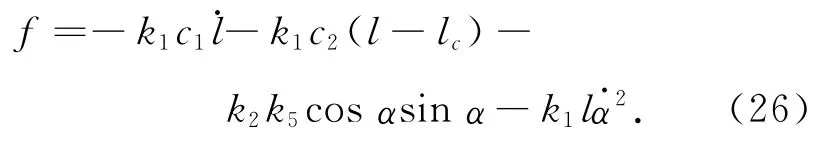
式（26）即為設計的內環控制律，是帶非線性補償項的PD控制器。式中lc即為外環控制律得到的。為保證內環實際輸出的滑塊位移幅值不超過經限幅的位移指令幅值，應適當配置PD控制參數c1，c2，使內環系統保持為臨界阻尼或過阻尼狀態。

同樣對滑塊驅力進行限幅器設計。定義驅動力最大幅值為fmax，限幅后驅動力為fsat，設計滑塊驅動力飽和限幅器

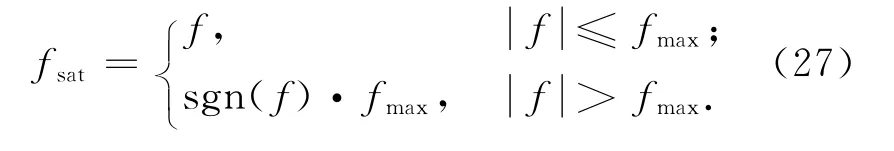
3 執行機構分配策略

為簡化姿態動力學模型，上述建模過程將沿對角線兩根導軌各自運動的雙滑塊等效為可沿帆面全對角線運動的單個滑塊，并對單滑塊設計控制律。但工程實現中，需將設計單滑塊控制律還原為雙滑塊控制律，即將單個滑塊的受控運動分配至運動位移分別恒正／恒負的雙滑塊上。

因滑塊實際運動中必然將電機驅動噪聲和摩擦力等干擾引入航天器系統，為減少滑塊運動過程對航天器動態可能的不良影響，采用運動分配策略

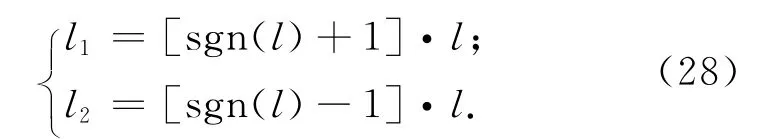
式中：l為等效滑塊的位移；l1為沿正向導軌運動滑塊的位移，且l1≥0；l2為沿負向導軌運動滑塊的位移，且l2≥0。采用上述執行機構分配策略，可保證任一時刻同對角線上僅有單個滑塊運動，盡可能減少滑塊運動對系統動態引入的干擾。

4 ADAMS-MATLAB聯合仿真

針對本文研究的帶移動滑塊太陽帆航天器，在ADAMS軟件中建立偏航通道實體動力學模型如圖4所示。航天器模型有關參數源自美國新千年計劃ST7（NMP ST7）的太陽帆實驗任務［8］。仿真物理參數為ms＝156kg；mp＝10kg（5kg×2）；J＝3 000kg·m2；d＝0.05m；單結構桿長度30m；PAU＝4.563×10－6N／m2；As＝1 400m2；Bf＝0.79；Bb＝0.55；ef＝0.05；eb＝0.55；r＝0.88；ρs＝0.94。

在實體模型上定義載荷。本文研究的太陽帆航天器在空間所受外力僅有作用于壓心Op處的光壓作用力。由光壓模型式（2）～（3）可知：光壓分力Ft，Fn大小由航天器姿態角α及表帆面光學參數決定。

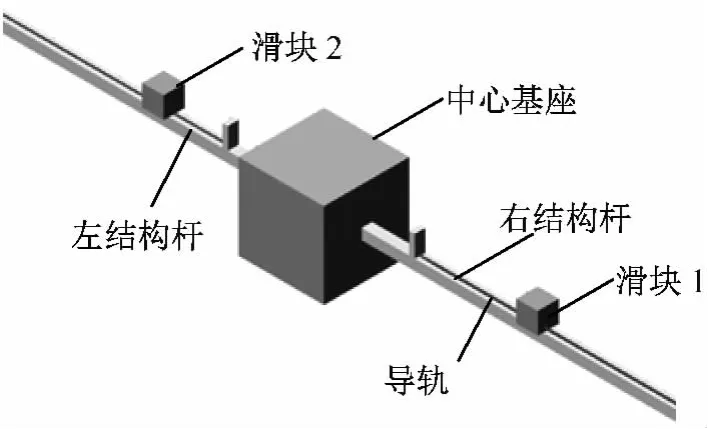
圖4 ADAMS建立太陽帆航天器仿真模型Fig.4 Simulation model of solar sail spacecraft in ADAMS

為定義ADAMS，MATLAB軟件間的數據交換接口，在ADAMS／Controls模塊中定義控制輸入變量為兩滑塊驅動力f1，f2，輸出變量為航天器姿態α，兩滑塊位移l1，l2及速度。數據交換變量定義完畢后，在Plant Export界面輸出聯合仿真所需的＊.m，＊.cmd，＊.adm接口文件。

在MATLAB中運行生成的m函數文件，利用接口命令adams＿sys生成含聯合仿真所需的Simulink模塊，其中adams＿sub模塊包含ADAMS軟件建立航天器非線性動力學模型及各輸入輸出信號接口。按上文設計控制律，以adams＿sub模塊為核心，在Simulink軟件中建立控制系統聯合仿真模型。

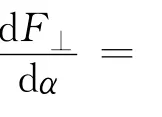
仿真取內環控制器參數c1＝60，c2＝10，外環控制器參數Q＝diag［103103］，R＝10，雙滑塊各自驅動力最大幅值1N，滑塊位移最大幅值28m。為驗證本文設計控制律對存在初始姿態角誤差和角速度誤差的太陽帆航天器的控制效果，并與傳統固定增益LQR控制律比較，取太陽帆初始姿態為（α0）＝ （－60°，－0.03 （°）／s），跟蹤目標姿態（αc，）＝（35°，0 （°）／s），取固定增益 LQR 控制律狀態反饋陣K0為系統在初始狀態 （α0）下線性化求解得到的反饋矩陣。仿真所得太陽帆航天器狀態變化如圖6～8所示。

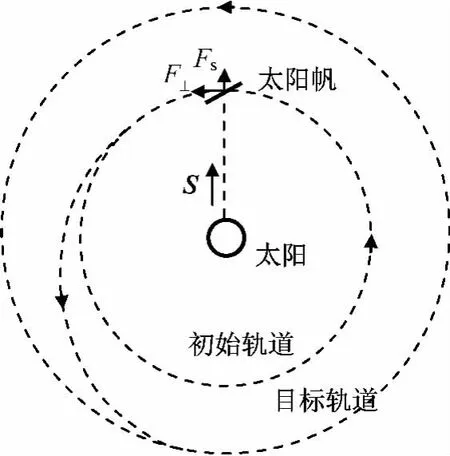
圖5 行星際太陽帆航天器變軌Fig.5 Interplanetary solar sail spacecraft’s orbit curve

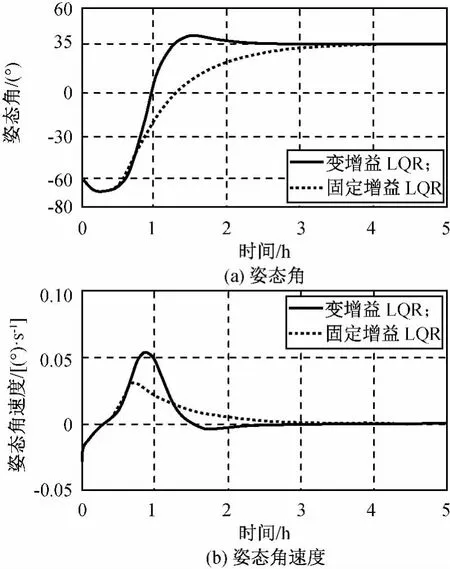
圖6 太陽帆航天器姿態變化Fig.6 Attitude of solar sail spacecraft

由圖6可知：外環采用變增益LQR和固定增益LQR控制律均可對太陽帆航天器姿態進行有效控制，固定增益LQR姿態控制耗時較長，航天器跟蹤至目標姿態需時約4h；變增益LQR控制律的控制效果明顯優于固定增益LQR控制律，航天器在約2h時間從初始狀態跟蹤至目標姿態階躍信號αc＝35°，之后滑塊僅需保持在配平點位置，使系統實際質心與壓心重合，無需維持大推力驅動即可抑制光壓干擾力矩，航天器姿態穩定在目標姿態處，實現太陽帆航天器大角度快速機動和長期姿態穩定的任務要求。

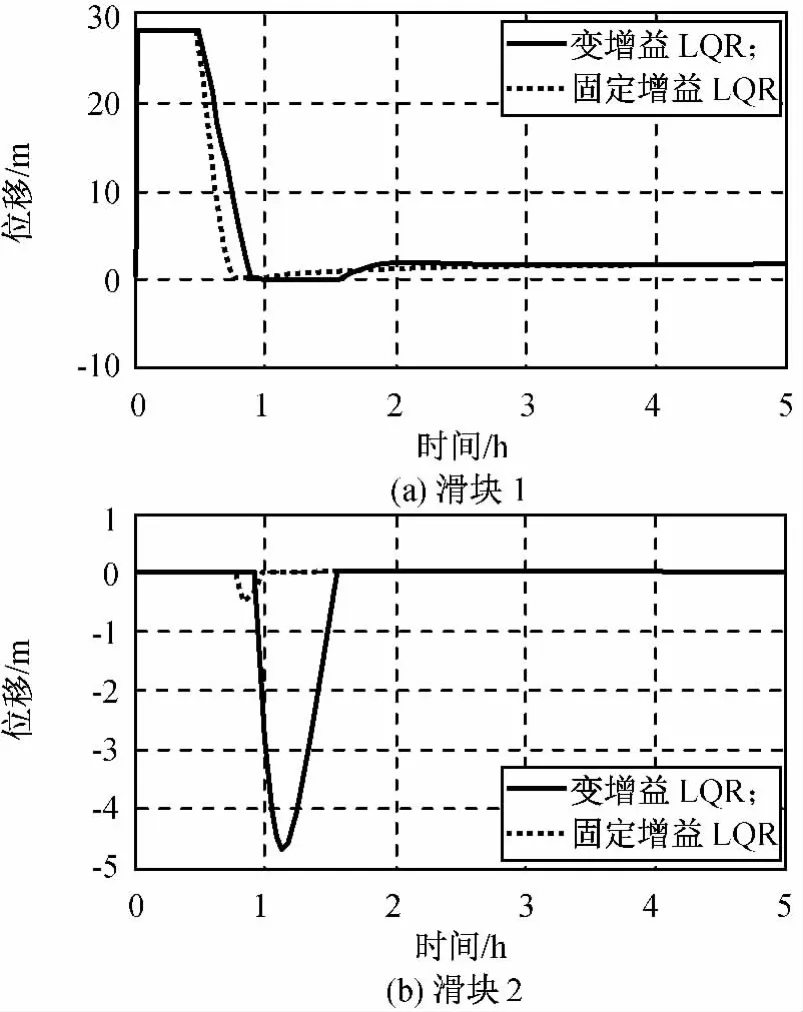
圖7 滑塊位移變化Fig.7 Displacement of moving mass

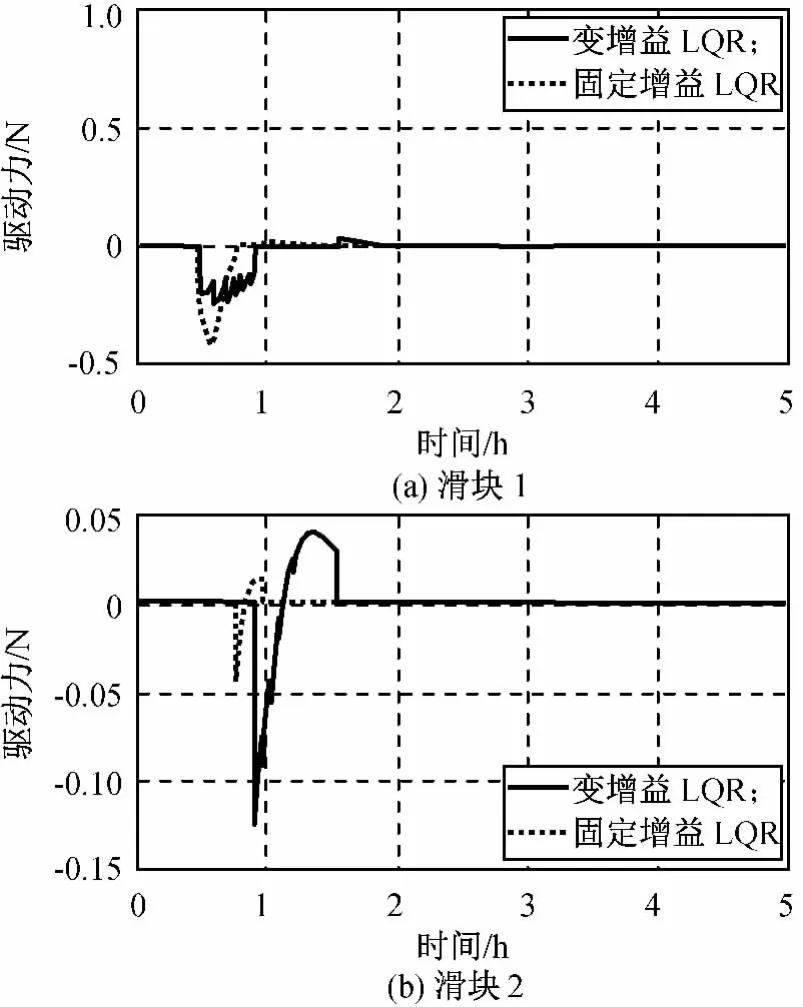
圖8 滑塊驅動力變化Fig.8 Driving force of moving mass

由圖7～8可知：姿態控制過程中滑塊位移l1，l2和驅動力f1，f2幅值均被限制在要求范圍內，設計飽和限幅器可有效限制系統控制輸入大小，且限幅后的控制輸入仍能滿足系統姿態控制的需要。

5 結束語

本文對基于移動滑塊的太陽帆航天器姿態控制方案進行了研究。以太陽帆航天器偏航通道為例，建立其姿態動力學模型，將姿態控制系統分解為外環和內環回路，分別設計了變增益LQR控制器和帶有非線性補償的PD控制器。在ADAMS軟件中建立航天器實體仿真模型，通過 ADAMS-MATLAB動力學聯合仿真實驗，對設計的姿態控制律的有效性進行了驗證。結果表明：設計基于移動滑塊的太陽帆航天器姿態控制方案，能針對存在初始角位置誤差和角速度誤差的太陽帆航天器進行有效的姿態控制，實現太陽帆航天器大角度快速機動，同時可滿足長期飛行任務中抑制光壓干擾力矩和保持姿態穩定的需求。與傳統帶控制桿或控制翼面的控制方案相比，基于移動滑塊的太陽帆航天器姿態控制方案具有結構簡單可靠，任務適應性強等特點，在未來太陽帆技術研究領域有重要價值。

［1］ McINNES C R.Solar sailing：technology，dynamics and mission applications［M］.Berlin：Springer，2004.

［2］ WIE B.Solar sail attitude control and dynamics，part 1［J］.Journal of Guidance，Control，and Dynamics，2004，27（4）：526-535.

［3］ JOHNSON L，YOUNG R，MONTGOMERY E，et al.Status of solar sail technology within NASA［J］.Advances in Space Research，2011，48（11）：1687-1694.

［4］ MURPHY D M，MURPHEY T W，GIEROW P A.Scalable solar-sail subsystem design concept［J］.Journal of Spacecraft and Rockets，2003，40（4）：539-547.

［5］ WIE B.Thrust vector control analysis and design for solar-sail spacecraft［J］.Journal of Spacecraft and Rockets，2007，44（3）：545-557.

［6］ THOMAS S，PALUSZEK M，WIE B，etal.AOCS performance and stability validation for large flexible solar sail spacecraft［C］／／41th AIAA／ASME／SAE／ASEE Joint Propulsion Conference ＆ Exhibit.Tucson：AIAA，2005：1-18.

［7］ 羅 超，鄭建華.采用滑塊和RSB的太陽帆姿態控制［J］.哈爾濱工業大學學報，2011，43（3）：95-101.

［8］ WIE B.Solar sail attitude control and dynamics，part 2［J］.Journal of Guidance，Control，and Dynamics，2004，27（4）：536-544.