基于流固耦合的高精度聲速剖面儀支撐結構的結構強度及應力分析

舒競翔，王收軍，李志偉，張寶峰

（天津理工大學 復雜系統控制理論及應用重點實驗室，天津 300384）

0 引言

聲速剖面儀是一種測量聲波在水中傳播速度的精密水聲儀器，同時通過溫度及壓力傳感器測量溫度和垂直深度，能夠快速、有效地為測深儀等聲吶設備校正測量誤差，提供實時聲速剖面數據[1]但在聲速剖面儀自身標定校驗時，需要設計出更高精度的聲速剖面儀與其他聲速剖面儀進行比對校驗，這就需要對高精度聲速剖面儀樣機機械結構提出更高的設計要求。支撐結構作為儀器整體機械結構的核心部件，其上安裝著一對相對的換能器，支架的受力變形將直接導致樣機測量數據精度的改變，所以對儀器支架結構進行力學分析尤為重要。對其強度和剛度分析具有十分重要的意義。而樣機是在海水攪拌的環境下工作的，所以儀器支架承受的是流體不均勻力的作用，所以采用流固耦合的方法進行分析。因此本文利用ANSYS Workbench平臺，對聲速剖面儀支撐結構進行單向流固耦合分析，計算出儀器支撐結構在海水攪拌中應力和變形量分布，為儀器的設計提供依據。

1 流固耦合分析方法

流固耦合是研究可變性固體在流場作用下的各種行為以及固體變形對流場影響這二者相互作用的一門科學。ANSYS很早就開始進行流固耦合的研究應用，目前算法和功能已相當成熟，本文采用ANSYS Mechanical APDL+FLUENT進行流固耦合分析。從數據傳遞角度出發，流固耦合分析分為單向流固耦合分析和雙向流固耦合分析。由于支架及攪拌設備的尺寸變形量相對于攪拌槽整體尺寸較小，即其結構變化對流場影響較小，所以采用單向流固耦合進行分析。

但是要對支架進行耦合分析前，需要先完場旋轉流場的計算，即一共進行兩個耦合計算，先進行攪拌器與流體的計算，得出帶有攪拌預應力的旋轉流場，然后將得出的流場域與支架結構進行另一個流固耦合計算，從而完成對支架的耦合分析。

1.1 流體控制方程

流體流動遵循物理守恒定律，基本的守恒定律包括質量守恒定律、動量守恒定律、能量守恒定律。

質量守恒方程[2]：

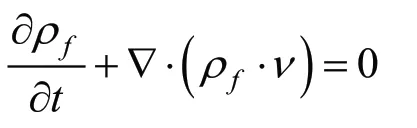
動量守恒方程：

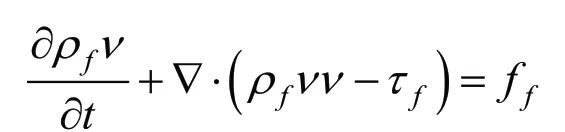
其中，t/s表示時間，ff表示體積力矢量。 fρ/（Kg/m3）表示流體密度，v表示流體速度矢量，fτ/（m/s）表示剪切力長量，可表示為：

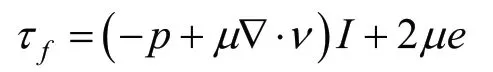
其中，p/Mpa表示流體壓力，μ/(N·s/m2)表示動力粘度，e表示速度應力張量

1.2 固體控制方程

固體部分的守恒方程可以由牛頓第二定律導出：

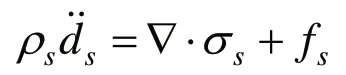
其中，sρ/（Kg/m3）表示固體密度，sσ 表示柯西應力張量， fs/ N表示體積力矢量，表示固體域當地加速度矢量。

1.3 流固耦合方程

同樣，流固耦合遵循最基本的守恒定律，在耦合交界面處，應滿足流體與固體應力（ fτ ）、位移（d）、熱流量（q）、溫度（T）等變量的相等或守恒，既滿足如下四個方程：

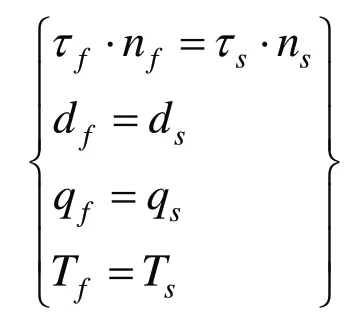
2 流固耦合數值計算

利用ANSYS Workbench進行流固耦合計算分析時，首先通過FLUENT軟件進行流場分析求得樣機支架上的壓力分布載荷，然后將求得的載荷導入Static Structural模塊中進行結構應力求解分析。

2.1 幾何模型建立

首先在SolidWorks中建立支架及攪拌器的幾何模型，然后導入到Workbench中FLUENT的前處理模塊Design Modeler中，再進行流場的建模。如圖1所示，攪拌葉片周圍的圓柱形區域空間為攪拌器流場域水體旋轉區，在這里將進行攪拌器葉片與靜止水體之間的流固耦合。其余三部分為攪拌槽流場域水體靜止區，其中中間部分為耦合區流場域水體靜止區，內部是樣機支架，在這里將進行流場域水體與樣機支架機械結構的流固耦合。

在網格劃分模塊Mesh中進行網格劃分，為了確保求解的精確性，對流場進行多域法網格劃分，耦合區域水體網格尺寸為10mm，下靜止區域水體網格劃分為面網格劃分，控制網格為10mm，上靜止區域水體網格劃分為四面體網格，采用默認值。劃分得到網格節點數為40798，單元數量為201771。流場網格模型如圖2所示。

圖1 支撐及攪拌和流場模型

圖2 流場域網格劃分

2.2 湍流模型選擇

選取流場模型時，選擇κ -ε 湍流模型。κ -ε型分為標準（standard）、RNGκ -ε 和帶旋流修正κ -ε 湍流模型。帶旋流修正的κ -ε 模型的優點是對于平板和圓柱射流的發散比率的更精確的預測。κ -ε 模型對于旋轉流動、強逆壓梯度的邊界層流動、流動分離和二次流有很好的表現。帶旋流修正的κ -ε 模型和RNGκ -ε 模型都顯現出比標準κ -ε 模型在強流線彎曲、漩渦和旋轉有更好的表現。所以針對這種特性選取帶旋流修正κ -ε（realizable）湍流模型。其方程[3]關系如下：

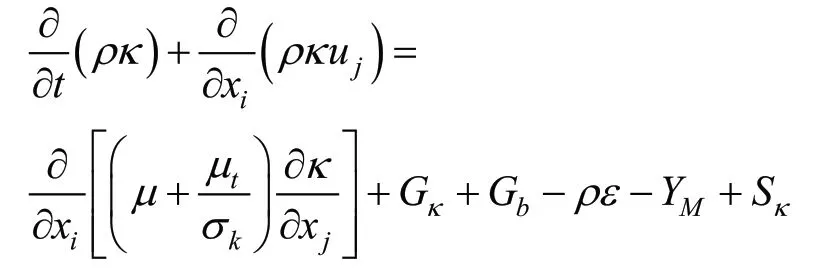
并擁有如下關系：

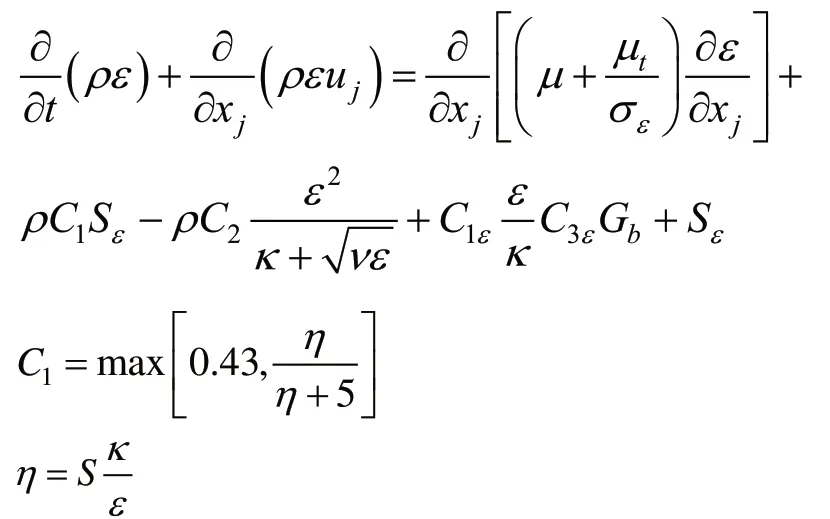
在方程中κ是湍流動能；ε為耗散率；Gκ是由層流速度梯度產生的湍流動能；bG 是由浮力而產生湍流動能；YM是可壓縮湍流中的擴散產生的波動值；1Cε、3Cε為經驗常數；R為修正項； κ? 和ε?為湍流動能和耗散率的湍流Prandtl數的倒數。相關常數如下：1Cε=1.42，C3ε=1.68。

2.3 流場參數及邊界條件

在實際的操作中流場內注入的是海水，根據海水的參數定義設置為海水的密度取1.025×103kg/m3，平均鹽度3.5%。定義攪拌器流場區水域旋轉區轉速為15rad/s葉輪的轉速為15rad/s，軸轉速同為15rad/s其余為靜止區，動靜區域之間設置為交互面（interface a），三個攪拌槽流場域水體，上部和中部兩個相鄰靜止區之間建立交互面（interface b）中部和下部兩相鄰靜止區之間建立交互面（interface c）。

2.4 流場求解

在流場求解方（Solution Methods）法選擇基本模式（SIMPLE），算法控制及監視器選擇系統默認。

進行求解初始化，選擇computer from all zones，進行流場初始化，最后設置迭代次數，選擇1500次，完成求解。計算在1226次完成收斂（！1226 solution is converged），如圖3所示。

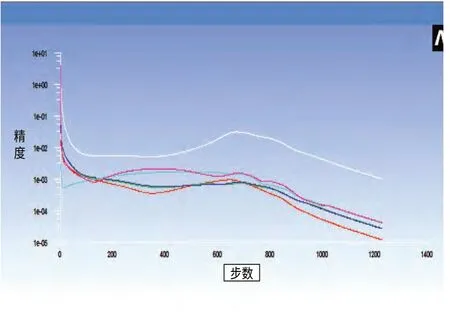
圖3 計算收斂曲線

得到流場的流速和應力云圖，如圖4和圖5所示，并得到支撐處的受力，約為3.25N。

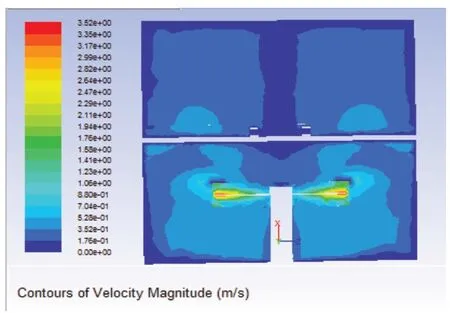
圖4 流場速率圖

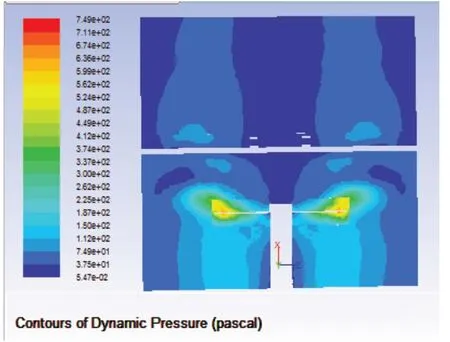
圖5 流場應力圖

2.5 流固耦合分析

對儀器支撐進行分析之前，需要材料參數的設置。材料選擇殷鋼(Invar Steel的音譯)，屬于鐵鎳合金的一種，其成分為鎳36%，鐵63.8%，碳0.2%。這種材料最大的特點就是隨溫度的變形極小，適合于制作對溫度變形有嚴格要求的零件。滿足儀器支撐需在海水中盡可能不受到溫度的影響，從而保證了對聲速測量的準確性。其密度ρ=7900kg/m3，彈性模量E=214GPa，泊松比ν=0.3。

進行儀器支撐的網格劃分，為了準確的得到流場分析中耦合面的節點壓力值，網格劃分尺寸與流場網格劃分尺寸一致，控制網格為10mm，劃分得到網格單元數為10540，節點數為19857。網格劃分結果如圖6所示。

圖6 儀器支撐網格劃分

對支撐施加載荷，在支架外圓周施加固定約束，在支架外表面耦合區施加來自FLUENT對流體計算完成的載荷，如圖7所示。從圖中可以得出安裝換能器位置的兩個孔受力為4.47×10-4MP，整個支架受到的最大應力為6.5×10-4MP，受到最小應力為1.9×103MP。

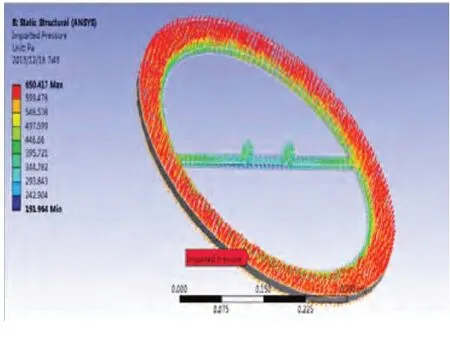
圖7 儀器支撐加載應力分布圖

加載完成后進行求解運算，得到總體應力云圖，如圖8所示；總體位移云圖，如圖9所示。

從圖8中可知儀器支撐兩邊部分承受的應力較大，中間部分也承受了較大應力，最大應力出現在支架橫梁與圓盤連接處，大小為0.1MP。

從圖9中可知儀器支撐的最大位移出現在支架中間部分，即安裝兩換能器之間的距離，其形變量為7.8×10-7m。

3 結論

本文通過運用流固耦合分析方法，進行了聲速剖面儀支撐結構在海水攪拌預應力下的結構應力分析，完成兩個流固耦合的數值模擬分析。

剖面儀支撐結構受旋轉海水預應力作用發生變形出現在支架結構中部，即兩個換能器之間區域。而最大應力出現在橫梁連接處，大小為0.1MP，滿足強度要求，證明設計安全可靠性。

兩換能器之間最大位移為7.8×10-7m，即7.8nm，產生變形較小，對換能器精度影響小，保證了高精度性，證明了設計的合理性。

[1]關致和,趙先龍,王莉娜.聲速儀標定系統[J].氣象水文海洋儀器,2004:38-42.

[2]關致和,趙先龍,王莉娜.HY1200系列聲速剖面儀[J].氣象水文海洋儀器,2004,02:53-57.

[3]李德軍,王潤田,卜安安.基于高精度時間測量技術的聲速儀設計[J].國外電子元器件,2006,06:20-22.

[4]袁啟銘.軸流泵葉片流固耦合震動特性分析[D].揚州大學,2009:23-25.

[5]祝克強,吳漢川,喬春.采用流固耦合的混砂車攪拌葉輪應力分析[J].現代制造工程,2012,03:51-54.

[6]唐學林,賈玉霞,王福軍.基于修正的RNGκ-ε模型的水翼空化數值模擬[J].工程熱物理學報,2012,09:1514-1518.

[7]Numerical Solution Of Fluid-Structure Interaction In Liquid-Filled Pipes By Method Of Characteristics[J].Chinese Journal of Mechanical Engineering,2007,03:44-49.

[8]施衛東,徐燕,張啟華.基于流固耦合的多級潛水泵葉輪結構強度分析[J].農業機械學報,2013,05:70-73+100.

[9]Numerical Investigation on Fluid Structure InteractionConsidering Rotor Deformation for a Centrifugal Pump[J].Chinese Journal of Mechanical Engineering,2011,04:539-545.

[10]解元玉.基于ANSYS Workbench的流固耦合計算研究及工程應用[D].太原理工大學,2011:33-35.

[11]婁濤.基于ANSYS的流固耦合問題數值模擬[D].蘭州大學,2008:14-18.