偏心對球形電容器耐壓能力的影響及偏心距的控制

王福謙 賈蘭芳

（長治學院 電子信息與物理系，山西 長治 046011）

同心球形電容器由于受力或工藝問題，可成為偏心球形電容器，這一變化將對該電容器的耐壓能力及電容量產生影響，使電容器不能正常工作。文章針對球形電容器的小偏心距情形，通過求解拉普拉斯方程得到偏心球形電容器內的電勢分布，再由場強分布研究偏心距對球形電容器耐壓能力和電容量的影響。

1 偏心球形形電容器內的電場

如圖1所示，偏心球形電容器內、外球殼的半徑分別為a、b，偏心距為c。以內球殼球心為原點，準確到c的一級小量，外球殼的方程為：

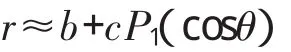
圖1 偏心球形電容器

對內、外球殼之間的任意一點 P（r，θ，φ），考慮到對稱性，由拉普拉斯方程▽2φ=0得兩球殼之間的電勢為：

在上式中取l=0，1兩項，則得電勢的近似值為：

式中C和D為c的小修正量。邊界條件為：

式中已經忽略了Cc和Dc。由文獻[2]，可令P0（μ）和P1（μ）的系數分別等于零，給出：

從中解得：

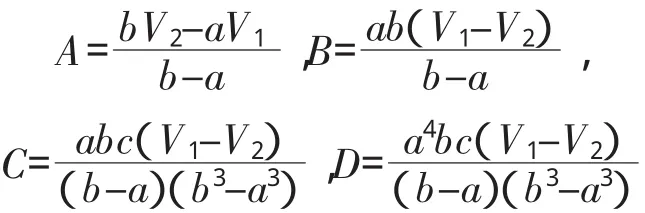
根據電勢與場強的關系，由式（1）有：

式（2）為偏心球形電容器內的場強分布。

圖2和圖3為利用MATLAB所繪制出的偏軸圓柱形電容器過圓心ο和ο'截面上的電場線與等勢線的分布圖。其中 a=5m、b=7m，V1=100V，V2=0V，偏心距c分別為0.0002m和0.0003m。

圖3 偏心球形電容器過圓心ο和ο'截面上的電場線與等勢線圖（c=0.0003m）

由圖2和圖3可以看出，在偏心球形電容器內部，愈靠近內極板表面，電場愈強，且兩極板間距最小處的內極板表面上的場強最大。

2 耐壓能力

偏軸圓柱形電容器內部場強最大處為兩極板間距最小處的內極板表面處，由式（2），取 r=a、θ=π，可得此處的場強為：

將有關數據 a=5m、b=7m，c=0.0005m，V1=100V，V2=0V。代入上式，可得：

而相同尺寸同心球形電容器，內極板表面處的場強為：

代入數據a=5m、b=7m，V1=100V，可得同心球形電容器內極板表面處的場強為：

比較式（3）式（5）可知，在電源電壓一定的情況下，偏心形電容器兩極板間距最小處的內表面上的場強要大于相同尺寸的同心球形電容器內極板表面的場強。所以，無論當同心球形電容器由于工藝問題還是受到外力作用發生偏心時，耐壓能力都將降低。

下面計算偏心球形電容器耐壓能力的改變量。由式（3）和式（5）可得，在介質的介電強度（即擊穿場強）一定的情況下，偏心球形電容器所承受的電壓Uo要小于同心球形電容器所承受的電壓Uc，在電容器所填充介質及其尺寸相同的情況下，偏心、同心電容器所承受電壓之比Uo/Uc為：

需要注意的是，以上兩式僅實用于偏心距較小的情形，當偏心距較大時，將出現較大的誤差，偏心距達到一定程度，偏心、同心電容器所承受電壓之比便不能由上式計算。

下面根據式（7）給出Uo/Uc隨偏心距c變化（a、b一定）的一組數據，以此來說明偏軸電容器的耐壓能力隨偏軸距的變化情況（表中c＞0.01m的Uo/Uc之值誤差很大，僅供參考）。

從表格1和表格2中的數據可以看出，若球形電容器的a=5m、b=7m，c=0.02m，知Uo/Uc=98.67%，此時該電容器的耐壓能力為其同軸時的約98.67%，取Uc=220V，則Uo=217.0740V；若電容器的 a=5m、b=7m，c=0.04m，知 Uo/Uc=97.37%，此時該電容器的耐壓能力為其同軸時的約97.37%，取Uc=220V，則 Uo=214.214V；若電容器的 a=9m、b=10 m，c=0.04m，知Uo/Uc=97.83%，此時該電容器的耐壓能力為其同軸時的約97.83%，取Uc=220V，則 Uo=215.5560V；若電容器的 a=9m、b=10m，c=0.04m，知Uo/Uc=95.76%，此時該電容器的耐壓能力為其同軸時的約95.76%，取Uc=220V，則Uo=210.672V。顯然，球形電容器由于偏心的作用，其耐壓能力將隨著偏心距的增大而降低，在偏心距一定的情況下，內、外球面的半徑差越小，耐壓能力降低的幅度越大。球形電容器在內、外球面半徑一定的情況下，偏心距超過一定程度，電容器將不能正常使用。

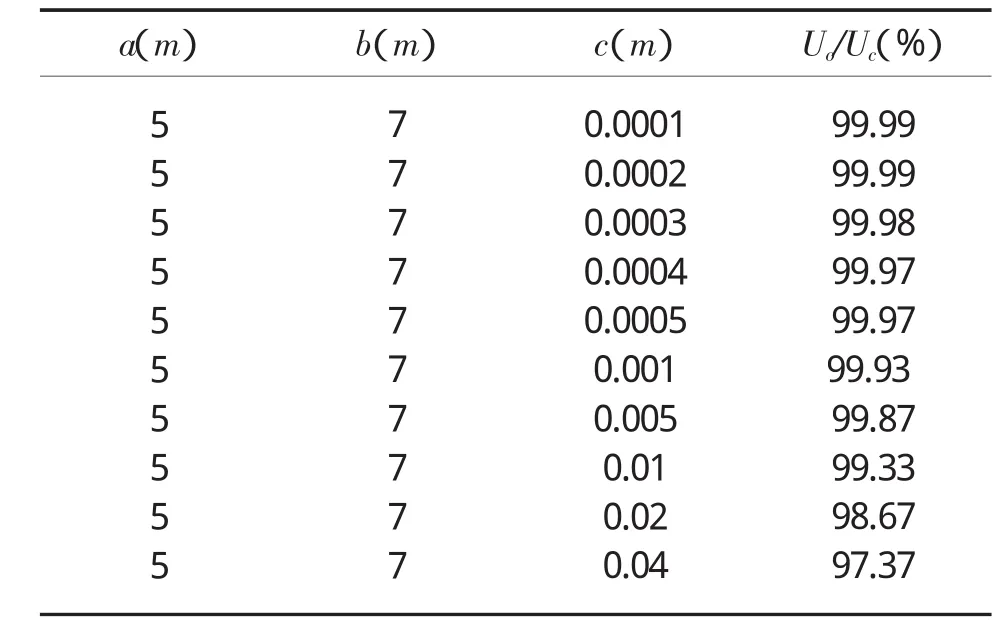
表1 耐壓能力Uo/Uc隨相對偏心距c的變化Tab.1 The change of voltage capability Uo/Uc with c

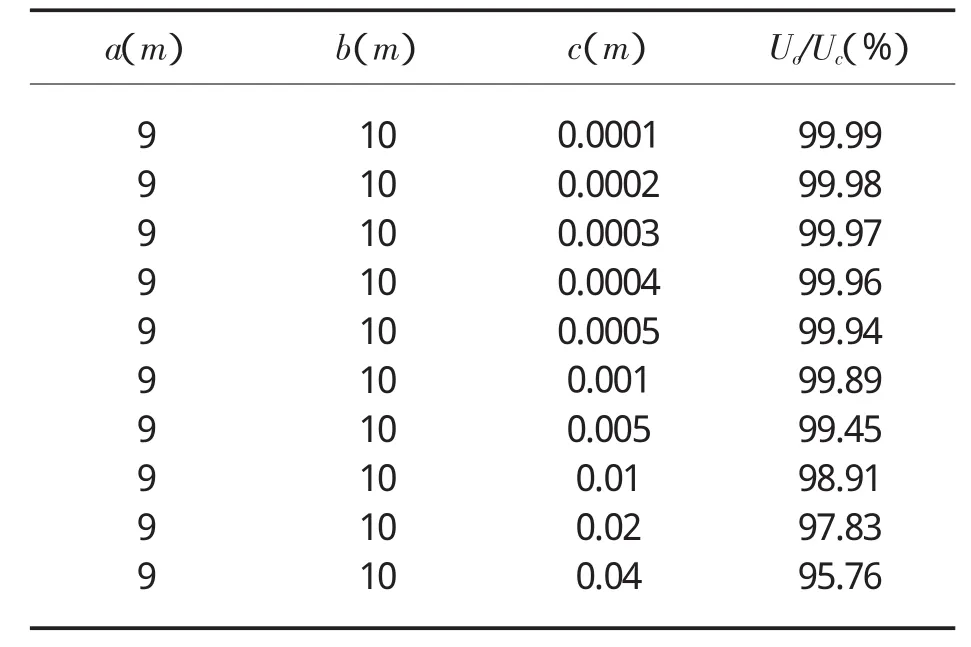
Tab.2 The change of voltage capability Uo/Uc with c

綜上所述，球形電容器由于工藝上出現的偏心，將直接影響到電容器的使用壽命和質量。由本文的結論可知，為保證電容器的質量和使用壽命，在生產工藝上要求盡量減小其偏心距，將其需控制在一定范圍之內。表1～2中所提供的電容器的耐壓能力隨偏心距的尺寸變化，數據供生產廠家參考。

圖4為利用Matlab所繪制出的同心球形電容器過圓心ο（ο'）截面上電場線與等勢線的分布圖。其中 a=5m、b=7m，V1=100V，V2=0V。

對圖4中內極板處電場線密度與圖2、圖3偏心球形電容器兩極板間距最小處的內表面上的電場線密度比較，也可以看出：偏心球形電容器兩極板間距最小處的內表面上的電場線密度較大，電場較強，表明其耐壓能力受偏心作用將降低。

圖4 同心球形電容器過圓心ο（ο'）截面上的電場線與等勢線圖

3 電容量分析

由式（1）可得偏心球形電容器內極板的面電荷密度為：

則偏心球形電容器的帶電量為：

由電容的定義可得偏心球形電容器的電容為：

4 結束語

文章將理論分析與計算機數值模擬相結合，通過對偏心球形電容器內電場的研究，不僅給出了其電場分布規律，分析了其耐壓能力隨偏心距的變化情況，而且還可為球形電容器的加工制作精度提供理論依據和參考數據，對提高球形電容器的質量，定量計算實際生產中出現的工藝偏差具有一定的參考價值。由于本文所討論的屬于球形電容器偏心率較小的情形，與生產實際相符合，因此，所得結論具有一定的實用價值。本文所使用的研究方法也可供電容器研究專業人員在新型電容器的設計和研發方面借鑒。

［1］劉金英等.物理學大題典：電磁學與電動力學［M］.北京：科學出版社，2005，10（1）：78-80.

［2］（美）W.R斯邁思著，戴世強譯.靜電學和電動力學［M］.北京：科學出版社，1981，1（1）：208-211.

［3］符果行.經典電磁理論方法［M］.成都：電子科技大學出版社，1998.156-158.

［4］康東.偏心球形電容器的理論分析與應用探討［J］.西安科技大學學報，2004，24（3）：365-368.