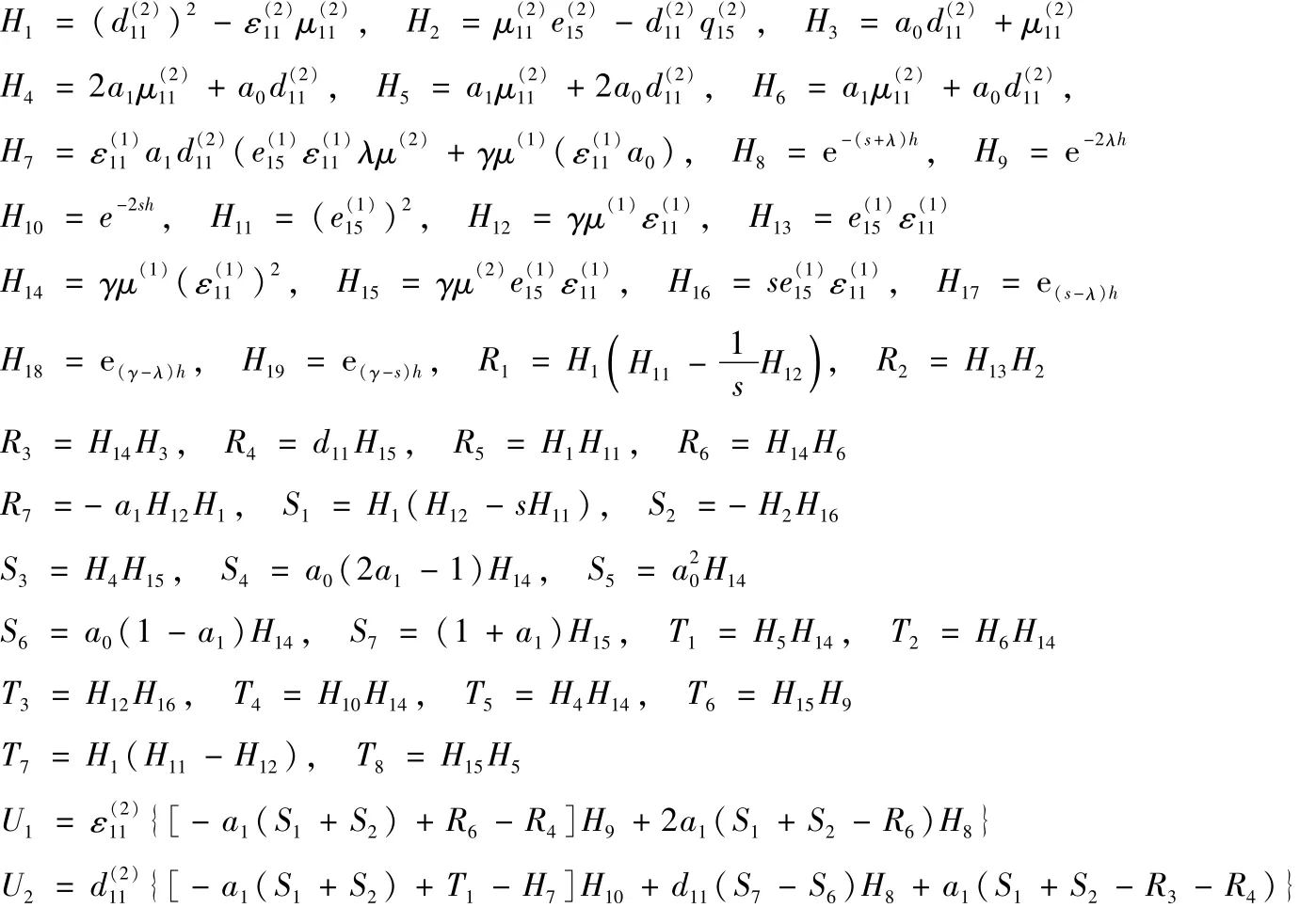壓電拼接電磁復合材料中裂紋對SH波的散射

楊 娟，李 星

（（1.寧夏大學 數學計算機學院，銀川 750021；2.寧夏大學 民族預科教育學院，銀川 750002）

電磁材料作為一類多功能材料，因其特有的電磁耦合效應在電子技術、超聲技術、智能工程及其它先進智能結構中得到廣泛應用。在電磁結構設計中對其缺陷研究意義十分重要。

裂紋為常見缺陷，預存于器件中或器件使用時因外荷載產生。隨探礦技術、無損檢測技術、雷達及聲納技術發展及對工程結構在動態載荷作用下問題研究，彈性波散射理論研究引起普遍關注。文獻［2－3］研究彈性復合材料中裂紋對SH波的散射。文獻［4］研究壓電纖維、彈性材料界面曲線型裂紋對反平面剪切波散射作用。文獻［5］研究正交各型異性功能梯度材料中裂紋對SH波散射。諸文獻均假設彈性波垂直入射，與實際情況不符。文獻［6］利用對偶積分方程方法研究了功能梯度壓電壓磁材料中裂紋對以任意角度入射的SH波的散射。文獻［7－8］考慮限制導通邊界條件下，假設SH波以θ角入射，利用Copson方法研究了功能梯度壓電帶拼接半無限大壓電材料及功能梯度壓電層拼接半無限大功能梯度材料中裂紋對SH波的散射。文獻［9］采用積分方程方法研究了功能梯度材料涂層下壓電底層中裂紋對SH波的散射。，現在還未見到有關壓電拼接電磁復合材料中裂紋對SH波的散射研究問題的報道。

本文利用積分變換技術結合求解對偶積分方程Copson方法研究壓電材料拼接電磁復合材料中裂紋對以θ角入射的SH波散射。用Fourier變換將混合邊值問題求解轉化為對偶積分方程求解。獲得裂紋尖端應力強度因子、電位移強度因子及磁通量強度因子。通過數值算例分析裂紋長度、裂紋到界面距離、入射角及波數對標準應力強度因子影響。

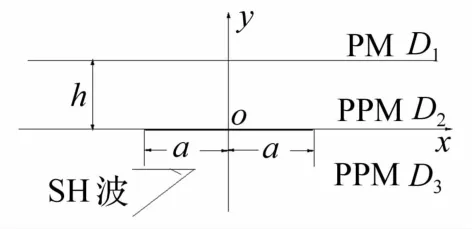
圖1 壓電材料粘接于電磁復合材料中裂紋對SH波散射的幾何模型Fig.1 Geometry of scattering of the SH wave on a crack magnetoelectroelastic composites bonded to a piezoelectric material

1 問題描述

考慮的問題見圖1，壓電材料粘接于下半平面為半無限大電磁復合材料，內含長2a裂紋，上半平面為半無限大壓電材料。xoy平面為各向同性面，與之垂直方向（z向）為極化方向。為描述方便，將結構分三個區域：裂紋以下為區域D3，裂紋至界面為區域D2，裂紋至界面距離為h，界面以上為區域D1。

SH波以θ角入射、作用于裂紋時，應力狀態為反平面剪切，屬斷裂力學意義的Ⅲ型裂紋問題。不為零位移僅有一個，即 w（x，y，t）為x，y的函數，t為時間變量。由波的疊加關系可知總波場、入射場及散射場關系為

式中：上標（t），（j）表示總位移場、入射場；w（x，y，t）為散射場。

壓電材料本構方程表示為

式中分別為壓電材料應力、電位移、電勢、剪切模量、壓電常數及介分別為電磁復合材料應力、電位移、磁通量、電勢、磁勢、剪切模量、壓電系數、介電參數、壓磁耦合系數、電磁耦合系數及磁導率。圖1中 k＝2，3分別對應 D2、D3區域。

設入射波為平面諧波，入射波形式為

因入射波、散射波時間因子相同，散射波場可寫為

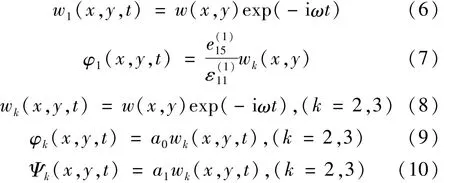
2 問題轉化及對偶積分方程獲得

問題的邊界條件為式中：2＝2x2＋2y2為二維 Laplace算子；ρ（1）為壓電材料密度；ρk為電磁復合材料密度；k＝2，3。

式（15）～式（19）經傅里葉變換后的解可假設為

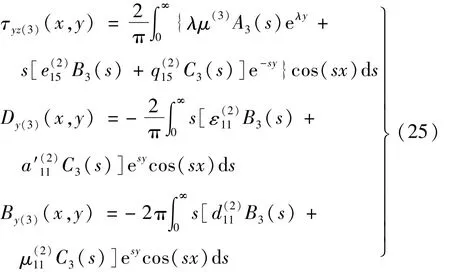
定義裂紋上下表面位移差為

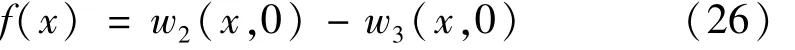
將式（21）、（22）代入式（26），并經 Fourier余弦變換，得

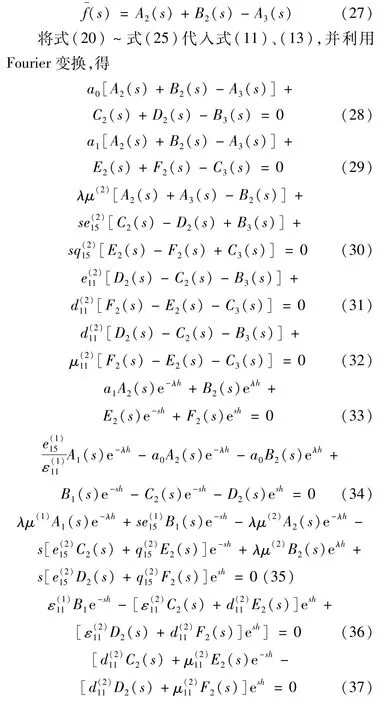
求解式（27）～式（37）獲得 A1（s），B1（s），A2（s），B2（s），C2（s），D2（s），E2（s），F2（s），A3（s），B3（s），C3（s）的解 （見附錄），并利用邊界條件（11）得對偶積分方程為

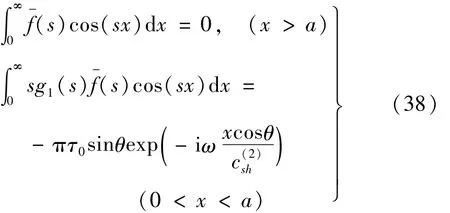
式中：g1（s）為已知函數，見附錄。

3 對偶積分方程求解

式中：J1（ ）為第一類一階Bessel函數。

將式（40）代入式（24），考慮裂紋尖端附近應力、電位移及磁通量在s→∞處奇異性，得y＝0時的應力、電位移、磁通量主部表達式為

定義標準化應力強度因子［10］為

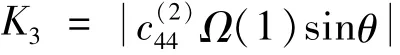
4 數值算例及討論

設（圖1）結構中壓電材料、電磁復合材料分別為PZT－4、BaTiO3－CoFe2O4，其結果見圖2～圖4。

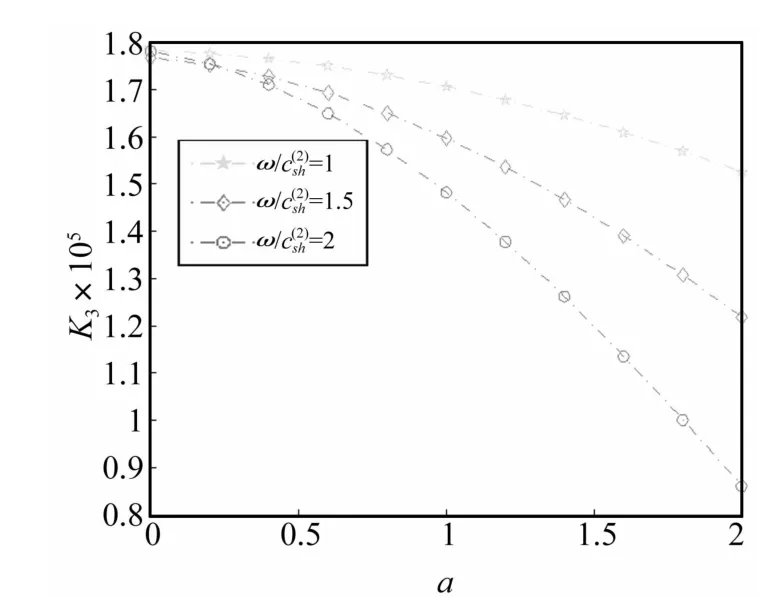
圖2 不同aω時標準化應力強度因子K3隨a變化關系Fig.2 Variations of the normalized stress intensity factor K3 with a for different aω

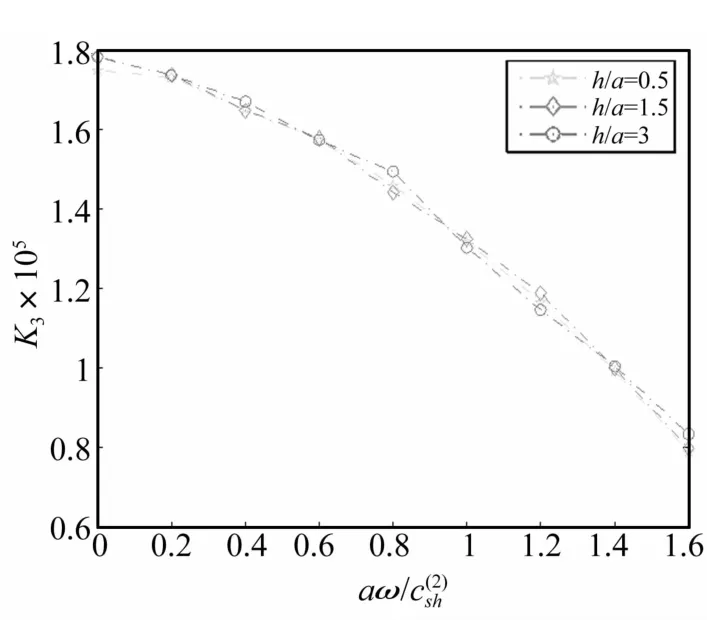
圖3 不同h／a時標準化應力強度因子K3隨aω／變化關系Fig.3 Variations of the normalized stress intensity factor K3 with aω／ for different h／a

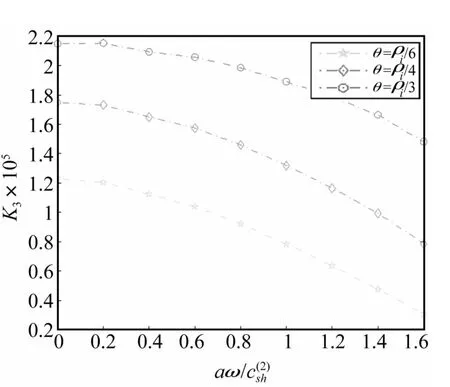
圖4 不同θ時標準化動應力強度因子K3隨aω／c（2）sh變化關系Fig.4 Variations of the normalized stress intensity factor K3 with aω at differentθ

（1）圖2為波數aω／c（2）sh變化時裂紋長度a對標準動應力強度因子影響（h／a＝0.5，θ＝pi／4）。由圖 2看出，aω越大標準動應力強度因子越小；aω一定時標準動應力強度因子隨a的增大而減小，而標準動應力強度因子在裂紋長度為0～0.3間即較接近。工程中可通過檢測裂紋長度變化預防因裂紋擴展造成的工件失效。

（2）圖3為不同裂紋至界面距離 h／a時波數aω對標準動應力強度因子影響（a＝0.5，θ＝pi／4）。由圖3看出，h／a對標準動應力強度因子影響不明顯。工程中適當控制裂紋至界面距離有利于提高材料的抗斷裂能力；h／a一定時標準動應力強度因子隨aω／的增大而減小。

（3）圖4給為入射角 θ變化時波數aω／對標準動應力強度因子影響（h／a＝0.5，a＝0.2）。由圖 4看出，標準動應力強度因子隨θ的增大而增大；θ一定時標準動應力強度因子隨aω的增大而減小。對相同入射頻率入射角越大。較大入射角可抑制標準動應力強度因子峰值出現，表明材料的標準動應力強度因子可通過入射角控制。適當調節載荷入射角可抑制材料的性質變化及裂紋擴展。

（4）由圖2～圖4知，標準動應力強度因子將隨波數 aω的增加而減小。因此工程中通過調整入射波頻率可降低裂紋尖端集中，通過改變入射波頻率實現應力場改變。

（5）由計算結果知，標準動應力強度因子不僅與裂紋長度、裂紋至界面距離、入射波頻率及入射角有關，亦與材料性質有關。

［1］Sih G C，Song Z F.Magnetic and electric poling effects associated with crack growth in BaTiO3－CoFe2O4 composite［J］.Theoretical and Applied Fracture Mechanics，2003，39（3）：209－227.

［2］Shen SP，Kuang Z B.Wave scattering from an interface crack in laminated anisotropic media［J］.Mechanics Research Communication，1998，25（5）：509－517.

［3］Zhou Z G，Shen SP.Scattering of harmonic elastic waves by a plane interface crack with linear adhesive tip in a layered half space［J］.Acta Mechanica Solide Sinica，1994，7（2）：105－113.

［4］Ueda S.Diffraction of antiplane shear wave in a piezoelectric laminate with a vertical crack［J］.European Journal of Mechanics A／Solids，2003，22（3）：413－422.

［5］Ma Lin，Nie Wu，Wu Linzhi，et al.Scattering of antiplane stress wave by a crack in a nonhomogeneous orthotropic medium［J］.Composite Structures，2007，79（2）：174－179.

［6］楊娟，李星.功能梯度壓電壓磁材料中裂紋對 SH波的散射［J］.應用力學學報，2008，25（2）：279－283.YANG Juan，LI Xing.Scattering of SH wave on crack in functionally graded magnetoelectroelastic materials［J］.Chinese Journal of Applying Mechanics，2008，25（2）：279－283.

［7］楊娟，李星.功能梯度壓電帶拼接半無限大壓電材料中裂紋對 SH波 散射的問題［J］.力學季刊，2010，31（4）：570－577.YANG Juan，LI Xing.Scattering of the SH wave on cracks in functionally graded piezoelectric strip bonded to a semiInfinite homogeneous piezoelectric［J］.Chinese Quarterly of Mechanics，2010，31（4）：570－577.

［8］楊娟，李星.SH波對功能梯度壓電層－功能梯度半空間中裂紋的散射［J］.西北師范大學學報（自然科學版），2013，49（6）：41－46.YANG Juan，LI Xing.Scattering of the SH wave on crack in functionally graded piezoelectric striphalf functionally graded space［J］.Journal of Northwest Normal University，2013，49（6）：41－46.

［9］LIXing，Liu Junqiao.Scattering of the SH wave from a crack in a piezoelectric substrate bonded to a halfspace of functionally graded materials［J］.Acta Mechanica，2009，208（3／4）：299－308.

［10］Bi X S，Chen J，Chen X L.Moving crack for functionally grated material in an infinite length strip under antiplane shear［J］.Theoretical and Applied Fracture Mechanics，2003，39（1）：89－97.

附錄