搖臂式起落架緩沖機構動態分析與優化設計

邱東海，賈宏光，馬伍元，高九州，周 凌

（1.中國科學院 長春光學精密機械與物理研究所，長春 130033；2.中國科學院大學，北京 100039）

隨無人機在軍事及民用領域的廣泛應用，對無人機地面運行特性要求亦日益增高，對起落架設計愈加苛刻［1］。不僅要求起落架有較高的結構強度，更需具備良好的動力學性能，以便保證飛機在著陸滑跑中承受的沖擊載荷小、穩定性好，遏制擺振現象發生［2－4］。

對起落架的設計、建模已有研究多集中于支柱式結構形式，主要通過建立起落架著陸時的動力學模型對緩沖器充填參數及油孔尺寸進行優化［5－7］，而對無人機搖臂式起落架研究較少。搖臂式起落架的緩沖性能除與緩沖器設計有關外亦與緩沖機構參數配置有關［8］。文獻［9］的搖臂式起落架初始設計方法未考慮緩沖機構尺寸對整體性能影響。文獻［10］通過虛擬樣機仿真分析起落架著陸沖擊時的動態響應，對起落架的緩沖性能進行校核。但僅考慮著陸沖擊無法滿足搖臂式前起落架的設計要求，需考慮滑跑中剎車、擺振等約束影響［11］，對起落架滑跑過程進行動態分析以確保設計的合理性。

本文針對某小型無人機搖臂式前起落架緩沖機構進行動態分析。建立滑跑時起落架數學模型，分析各工況前輪承受的載荷，計算無人機防止擺振所需約束條件，討論緩沖機構性態及方案。通過多學科優化平臺iSIGHT集成動力學軟件Adams對緩沖機構尺寸及剛度進行優化，并對優化后的起落架進行滑跑與靜剛度試驗，分析與評價試驗結果。

1 工程問題描述

該小型無人機起落架方案為前三點式布局，見圖1。該布局利于主輪受到擾動時運動相對穩定，著陸猛烈剎車時飛機不致向前翻倒。考慮起落架結構簡單緊湊，采用差動剎車轉向方式，配合該方案前起落架采用自由定向式，并選搖臂式緩沖機構。

圖1 無人機起落架示意圖Fig.1 Schematic diagram of the landing gear

滑跑中剎車操縱主要有點剎轉向與剎死制動，剎死時主輪摩擦力在前輪處會產生巨大俯仰力矩。若只考慮起落架地面隔振的濾波作用，則會導致起落架設計剛度過低、剎死制動時無人機出現低頭現象。因此需對前起落架動態特性進行分析，并對緩沖機構進行優化設計，使起落架滿足減振緩沖功能的同時亦能遏制擺振現象發生。

2 起落架動態分析

2.1 擺振

當飛機滑跑達一定速度時前輪會發生偏離其中立位置的劇烈側向擺動，導致前起支柱與機身晃動甚至形成整個機身從頭至尾顫抖，稱為前輪擺振。擺動的動力平衡方程為

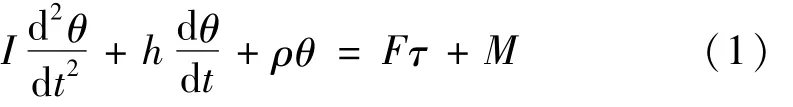
式中：θ為擺動角；I為轉動慣量；h為擺動阻尼系數；ρ為擺動彈性拘束；τ為穩定距；F為側向力；M為輪胎扭轉力矩。

防止前輪擺振的最有效措施為安裝減擺器，因此研究擺振問題歸結為判斷該微分方程的穩定性，通過拉氏變換求得方程的特征根，若特征根均在虛軸左半平面則系統穩定。用該方法可求得臨界穩定條件時減擺所需臨界阻尼，設計減擺器。

式中：β／α為爬行距；α，β為輪胎滾動系數，由機輪參數特性求得。

起落架穩定距 τ滿足［12］式（2）時系統是穩定的，飛機不會發生擺振現象。基于此本文采用增大穩定距方式遏制擺振發生，獲得τ的最小值為105 mm。

2.2 剎車

滑跑過程中無人機因氣動力變化及剎車操縱導致前起落架的承受載荷并不處于恒定狀態。為使緩沖性能滿足滑跑各工況，對無人機進行全面動力分析，見圖2。圖中an為前輪至重心的距離；am為主輪至重心距離；h為重心高度；H為發動機推力作用點至重心距離；φp為發動機安裝角；Pn，Pm分別為前輪、主輪支反力；Qn，Qm分別為前輪、主輪摩擦力；T為發動機推力，在剎車剎死與著陸階段T＝0；L，Mq分別為氣動升力與氣動俯仰力矩。

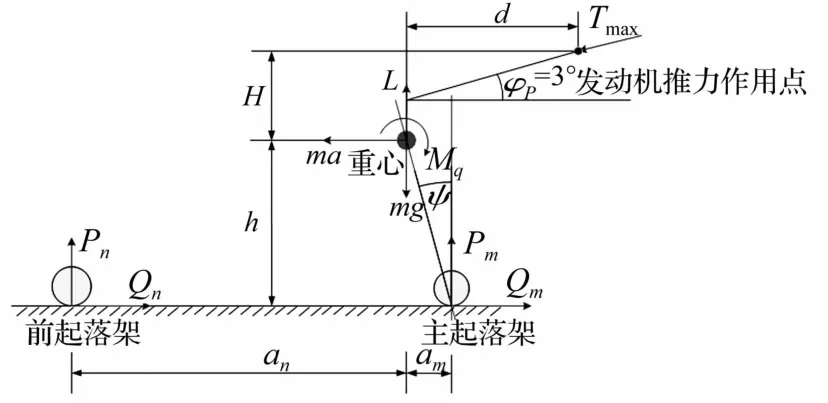
圖2 無人機滑跑受力示意圖Fig.2 Schematic diagram of UAV ground force

由于滑跑中俯仰角、滾轉角為零，三輪胎未離地，可得法向力、水平力與俯仰力矩三個平衡方程，從而求出支反力Pn，Pm與慣性力ma的解析表達式。

法向力平衡方程為

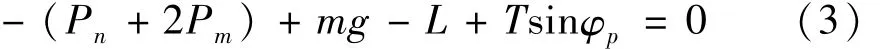
水平力平衡方程為

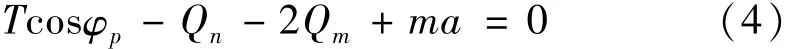
繞主輪的俯仰力矩平衡方程為

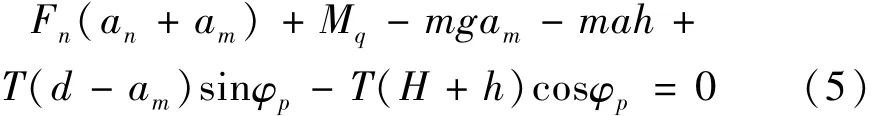
式中：Qn＝μnQn；Qm＝μmQm；μn＝0.05；μm值由剎車情況而定。

由于剎車操縱時無人機處于低速狀態氣動力較小，因此定義L＝Mq＝0，求解前輪在三種工況下的支反力，即：① 機輪剎死、發動機處于無推力狀態，得Pn＝553 N；② 機輪不動、無人機處于試車狀態慣性力為0，得Pn＝482 N；③ 機輪點剎、發動機處于有推力狀態，得Pn＝370 N。由分析看出，前輪承受的最大支反力為553 N。

2.3 著陸

此階段起落架須能消耗、吸收無人機著陸撞擊時產生的巨大能量，防止結構發生破壞。正常著陸時無人機有一定迎角，緩沖吸能主要由主起落架完成；但因操縱不當導致飛機以水平姿態著陸時前起落架應有一定能量儲備。據本無人機技術要求，在前機輪下沉位移145 mm內起落架需有52 J以上的能量儲備。

2.4 約束條件

前起落架緩沖機構約束條件為：① 停機狀態Pn＝210 N，緩沖器不壓縮；② 點剎。有推力工況Pn＝370 N，緩沖器允許壓縮小于5 mm位移，飛機不發生低頭現象；③ 機輪不動、無人機處于試車狀態Pn＝482 N，緩沖器允許壓縮，但不能超過半個使用行程；④ 剎死、無推力工況Pn＝553 N，緩沖器允許壓縮，但需留一定余量；⑤ 飛機以水平姿態著陸，在前機輪下沉位移145 mm內，起落架需52 J以上的能量儲備。

3 緩沖機構性態分析

3.1 緩沖機構設計計算模型

圖3為搖臂式前起落架結構圖，該起落架由前輪叉、緩沖器與支柱組成，形成一三角區，當前輪受載荷時前輪叉相對鉸鏈點轉動，帶動緩沖器壓縮至一定行程。該形式的起落架可承受前方沖擊載荷，使飛機在地面滑跑時更平穩。

據繞前輪叉上鉸鏈點的力矩平衡方程，可得作用于緩沖器的載荷為

式中：Fn為緩沖器承受載荷；ln，ls分別為前輪、緩沖器力臂。

由式（6）知，前輪支反力確定后緩沖器所受載荷由力臂比ln／ls決定。由圖4幾何關系可得緩沖器及前輪載荷力臂之比關系為

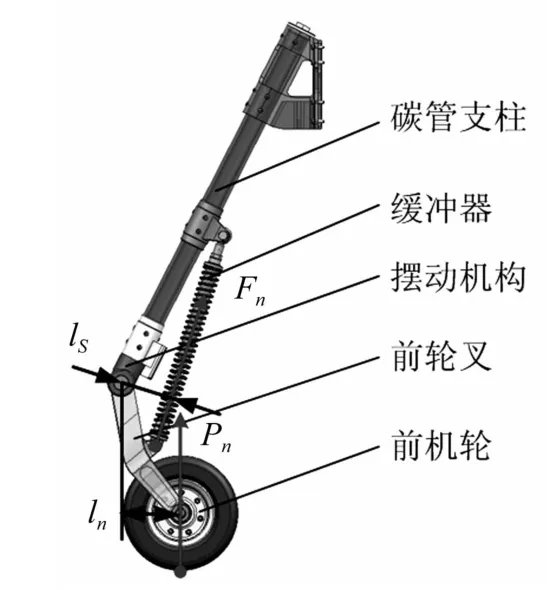
圖3 搖臂式前起落架Fig.3 Articulated landing gear

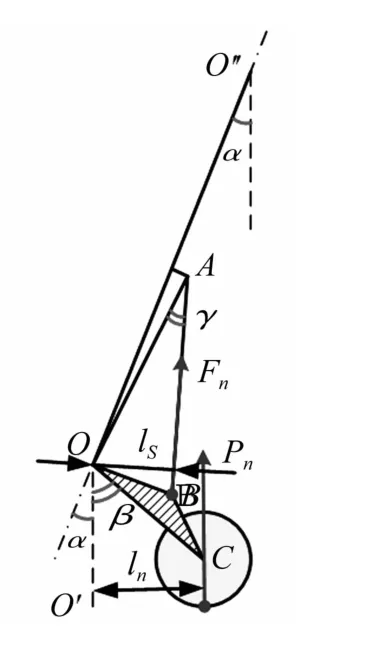
圖4 起落架機構示意圖Fig.4 Cushioning mechanism

式中：lm為緩沖器長度；Δl為緩沖壓縮行程。

聯合以上方程可求得力臂比的解析表達式為

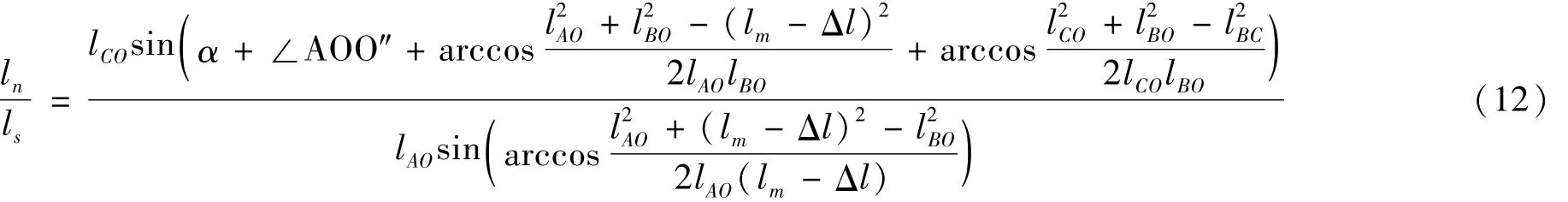
3.2 緩沖器技術參數

緩沖器由80 mm行程的氮氣彈簧與壓縮彈簧并聯組成。參考氮氣彈簧產品樣本剛度線性較好，樣本的軸向力與壓縮行程關系為

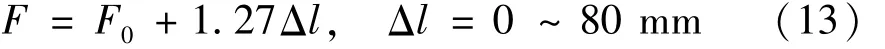
式中：F0＝300 N為氮氣彈簧預壓縮力。

定義壓縮彈簧剛度為Ks，整根緩沖器軸向力為

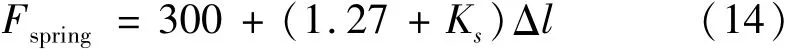
3.3 緩沖機構方案

合理設計應使緩沖機構既能有效緩沖路面沖擊，又具有一定著陸吸能儲備。滑跑工況為保持飛機姿態平穩，緩沖器行程不應過大。而著陸工況，由于沖擊能量較大，緩沖器應充分發揮使用潛力。為評判滑跑工況下緩沖器的壓縮行程，本文引入緩沖比 λ＝Fspring／Fn，其中 Fspring為緩沖器實際的彈性回復力，Fn為地面等效載荷，即地面載荷通過緩沖機構傳遞至緩沖器的作用力。

為確定緩沖機構設計方案，對剎死工況Pn＝553 N給出緩沖比設計過程中的3種情況，見圖5。由圖5看出：① 整個行程中λ＞1時緩沖器預壓縮力大于地面等效載荷，緩沖器無法壓縮；② 緩沖器初始輸出彈性回復力不足以平衡地面載荷，緩沖壓縮行程增加，在Δl0處機構達到平衡；③ 整個行程中λ＜1時緩沖器出現壓縮到底情況。因此選方案②，緩沖機構既可有效緩沖沖擊（漸增性），又能使緩沖器保留一定緩沖余量。

將式（6）、（14）代入緩沖比計算式，得

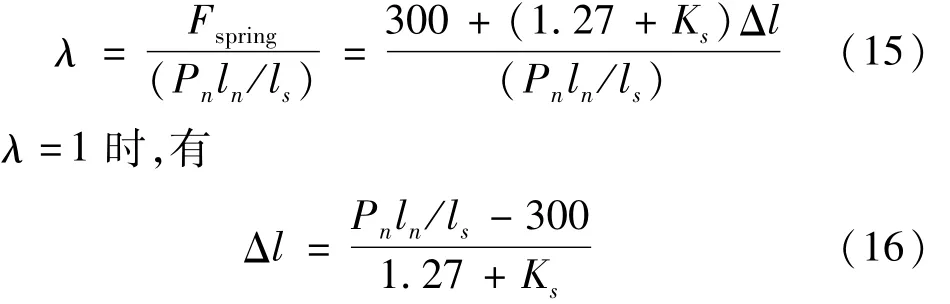
由式（16）知，前輪載荷Pn確定情況下通過改變彈簧剛度Ks及力臂比ln／ls的大小，可調整緩沖器的壓縮平衡點。

3.4 壓縮彈簧剛度分析

彈簧設計需滿足剪切強度、剛度約束條件，即

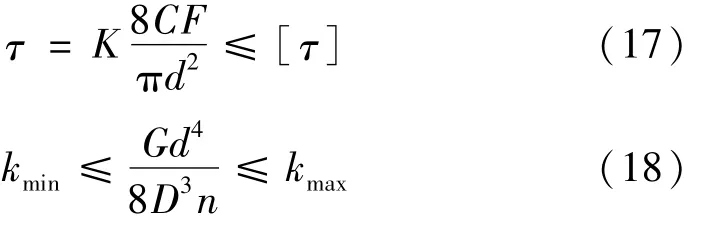
式中：G為切變模量；d為鋼絲直徑；D為彈簧中徑；n為彈簧工作圈數；K為補償系數；C為彈簧旋繞比；F為工作載荷。

由上兩式可得結構允許的彈簧剛度范圍為4.7～11 N／mm。只更換壓縮彈簧，修改起落架成本最小，因此在不修改起落架結構前提下適當增大彈簧剛度，驗證緩沖結構是否滿足要求。圖6為前版起落架緩沖比。由圖6看出，點剎時緩沖器已壓縮較大位移67 mm。修改彈簧剛度，令Ks＝10 N／mm，得緩沖比曲線見圖7。由圖7看出，緩沖性能獲得改善，但該方案只滿足1、4約束條件；點剎、試車工況緩沖器仍出現大壓縮位移。因此僅修改彈簧剛度不能滿足預想要求，須對起落架緩沖機構進行優化。

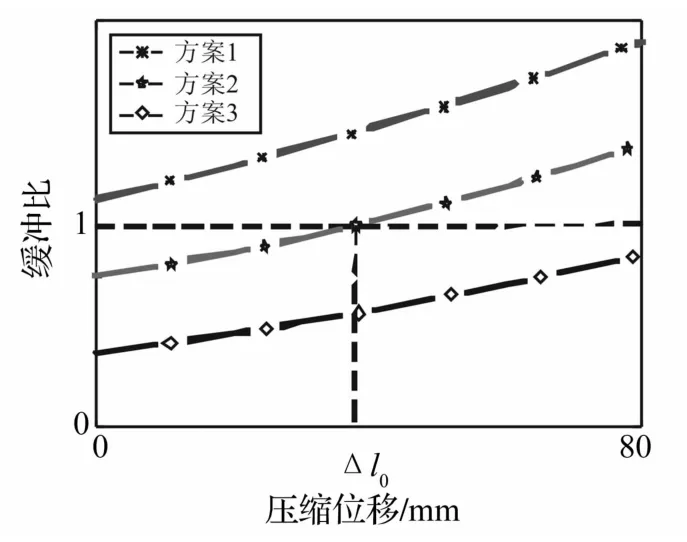
圖5 緩沖機構方案Fig.5 Scheme of cushioning mechanism

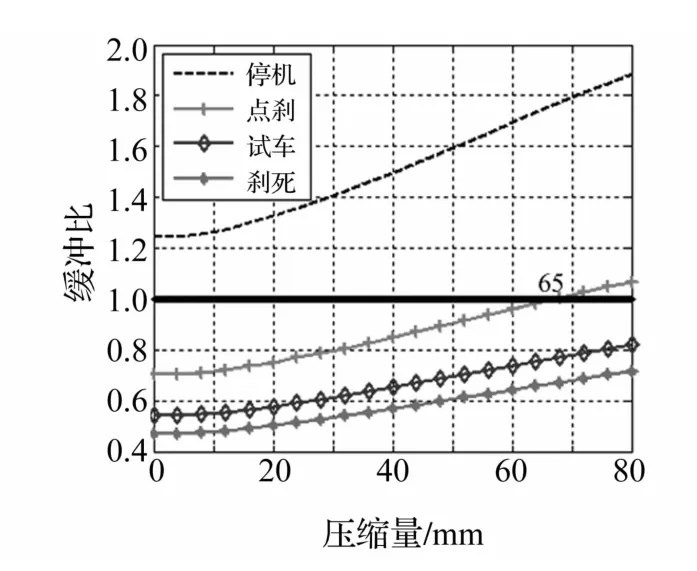
圖6 原模型緩沖比Fig.6 Buffer ratio of original model

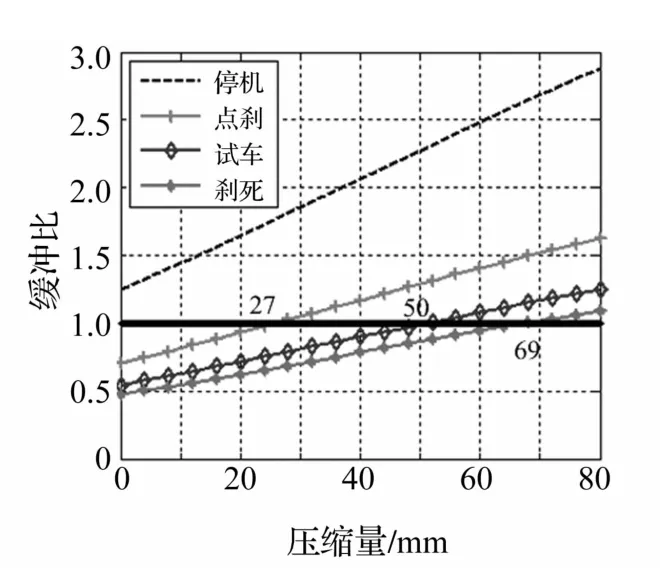
圖7 更換彈簧模型緩沖比Fig.7 Buffer ratio of change spring model

4 起落架緩沖機構優化設計

4.1 優化模型建立

優化設計模型一般包括設計變量、目標函數、狀態約束條件等。建立緩沖機構優化數學模型。

（1）設計變量。在以上分析基礎上考慮結構的允許條件，設計變量為壓縮彈簧剛度Ks、穩定距τ、傾斜角α。通過Adams對起落架參數化模型進行靈敏度分析，獲得A、B兩點對緩沖性能影響的敏感程度最大，因此增加結構尺寸lAB，lBO為設計變量。寫成向量形式為

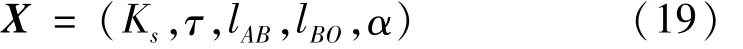
（2）可行域。由受力分析所得穩定距及起落架結構尺寸共同決定，限定為

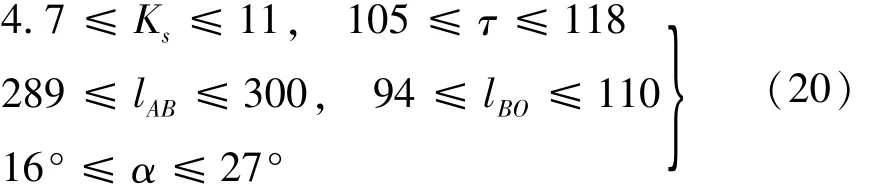
（3）目標函數。使起落架在沖擊載荷下緩沖器所受軸向力Fn最小，即

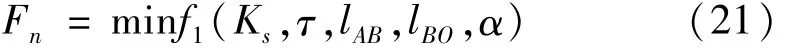
（4）約束條件。即動態分析所得起落架緩沖機構約束條件。

4.2 優化設計方法與優化結果

由于彈簧剛度Ks不影響緩沖機構力臂比，因此將該變量置于最外環，采用針對Ks的遍數法，對其它變量采用序列二次型規劃法，全域最大優點為可取可行域中所有滿足約束條件自變量點的最小值，具體流程見圖8。

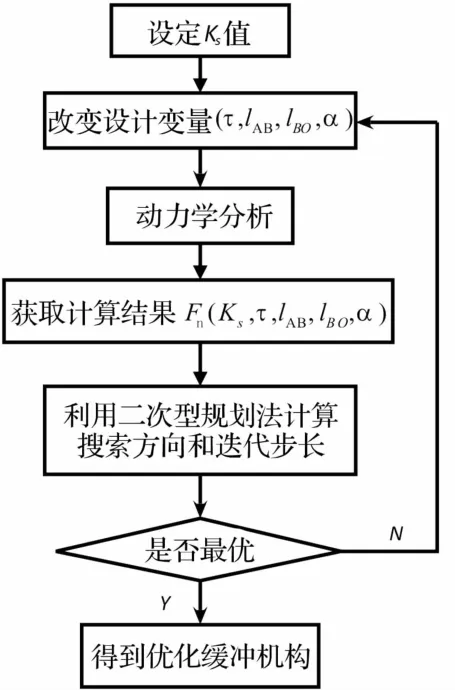
圖8 優化流程Fig.8 Optimization chart

據優化模型采用 Adams動力學軟件對起落架緩沖機構進行參數化建模，建立起落架虛擬樣機模型，利用iSIGHT多學科優化平臺集成Adams，實現緩沖機構優化。目標函數變化趨勢見圖9，可見力臂比的優化對降低軸向力作用巨大；而僅修改結構參數時緩沖器軸向力由初始708 N降為403 N，降低43%。

對彈簧剛度進行優化獲得變量數據見表1。優化后模型各工況緩沖比曲線見圖10。由圖看出，壓縮位移均滿足預想要求。

表1 優化前后變量數據對比Tab.1 Comparison of variable data between per and post optimization

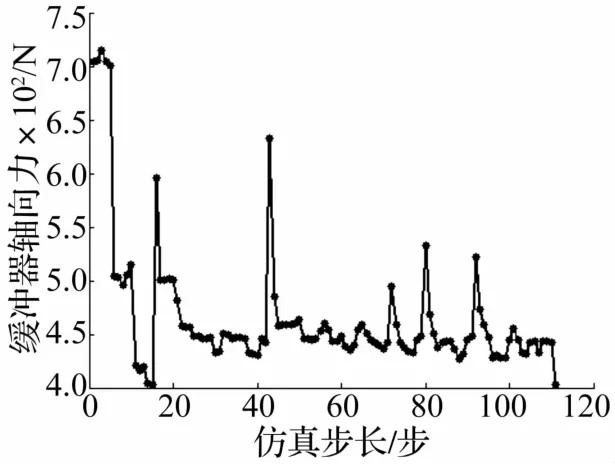
圖9 緩沖器軸向力監視器Fig.9 Monitor of force of shock absorber

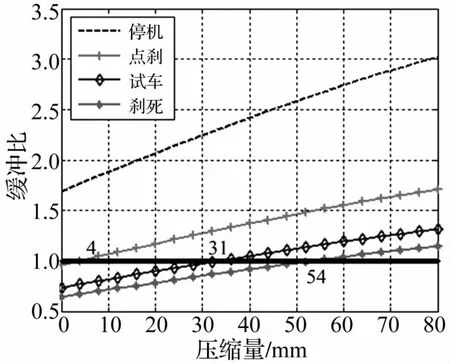
圖10 優化模型緩沖比Fig.10 Buffer ratio of optimal model

5 試驗驗證

考慮安全及成本，本文用三輪等比小車進行滑跑試驗。小車采用沙包配重模擬無人機重量，并利用吊籃位置調整保證小車與無人機質心一致，見圖11。滑跑過程中小車由牽引車牽引，達到預定速度時釋放牽引，觀察小車的剎車響應。由于小車無法模擬2、3工況起落架受力，因此對剎死無推力工況進行試驗，發現緩沖器未壓縮到底仍有一定緩沖余量。由此判斷設計的起落架安全，可進行無人機滑跑試驗。試驗中無人機運行平穩，未發生擺振現象。表2為剎車等操縱所測試驗數據，與理論值進行對比看出兩者數據較吻合，偏差主要由緩沖器摩擦力影響所致。點剎工況時緩沖壓縮位移由原65 mm降低為3 mm，其它工況壓縮位移亦滿足預定要求。

圖11 三輪滑跑小車Fig.11 Threewheel taxi car

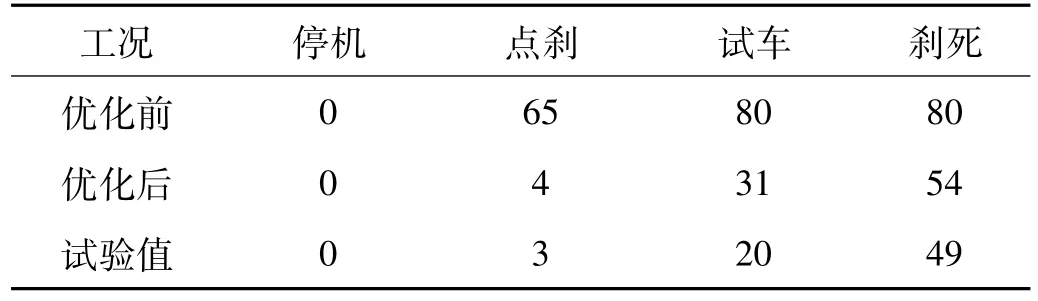
表2 優化前后緩沖器的壓縮位移／mmTab.2 Shock absorber compression displacement of pre and post optimization／mm

對起落架進行靜剛度試驗，將小車吊籃位置前移，逐步增大前輪載荷，測量所受載荷與法向壓縮位移，并進行曲線擬合獲得兩者關系曲線見圖12。由圖12看出，優化后緩沖器特性由硬彈簧轉換為軟彈簧，緩沖效率得到明顯提升。曲線包絡面積即為所吸能量，機輪下沉位移達到145 mm時，吸收能量由原44.6 J增大為76.5 J，提高71.5.%。此時緩沖器壓縮位移為75 mm，使用潛力得以充分發揮。

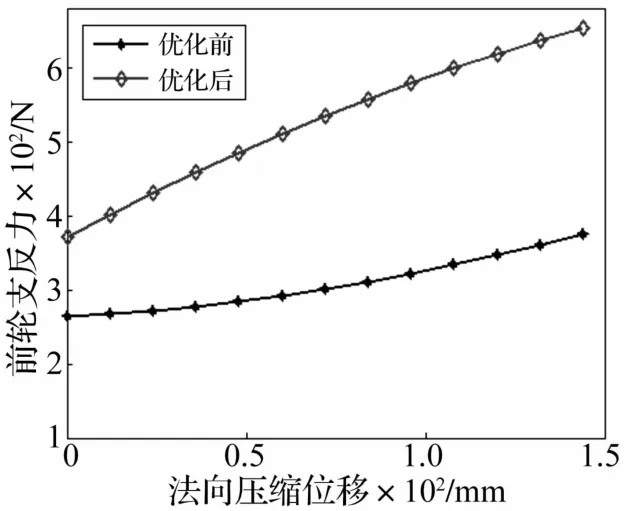
圖12 緩沖吸收功量對比Fig.12 Comparison of energy of shock absorber

6 結 論

（1）通過對搖臂式起落架動態分析，建立滑跑時起落架數學模型，分析無人機剎車操縱對前輪受力影響。通過分析擺振獲得遏制擺振發生的約束條件，并在此基礎上討論緩沖機構的性態與方案。

（2）以多學科優化軟件iSIGHT為平臺，集成動力學軟件Adams對緩沖機構進行優化。優化后對起落架進行滑跑與靜剛度試驗驗證結果表明，各工況下緩沖機構壓縮位移達到預想要求，能量吸收提高71.5%，無人機在滑跑中未發生擺振現象。

［1］Khapane P D.Gear walk instability studies using flexible multibody dynamics simulation methods in simpack［J］.Aerospace Science and Technology，2006，10：19－25.

［2］Gerhard S.Shimmy analysis of a simple aircraft nose landing gear model using different mathematical methods［J］.Aerospace Science and Technology，1997，8：545－555.

［3］Wolf R K.Recent developments at the numerical simulation of landing gear dynamics［J］.CEASAeronaut，2011，1：55－68.

［4］高澤迥.飛機設計手冊第14分冊：起飛著陸系統設計［M］.北京：航空工業出版社，2002：680－712.

［5］Lernbeiss L，Plochl M.Simulation model of an aircraft landing gear considering elastic properties of the shock absorber.［J］.Multibody Dyn，2007，221：77－86.

［6］劉小川，馬曉利，孫俠生，等.基于響應面方法的多支柱起落架著陸緩沖性能優化［J］.振動工程學報，2010，23（3）：305－309.LIU Xiaochuan， MA Xiaoli， SUN Xiasheng， et al.Performance optimization of shock absorber for multistrutlanding gear based on RSM［J］.Journal of Vibration Engineering，2010，23（3）：305－309.

［7］晉萍，聶宏.起落架著陸動態仿真分析模型及參數優化設計［J］.南京航空航天大學學報，2003，35（5）：498－502.JIN Ping，NIE Hong. Dynamic simulation model and parameter optimization for landing gear impact［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2003，35（5）：498－502.

［8］王明義，賈玉紅.基于能量法的緩沖器參數設計［J］.振動與沖擊，2005，24（6）：117－119.WANG Mingyi， JIA Yuhong. Design of absorber performance based on energy method［J］.Journal of Vibration and Shock，2005，24（6）：117－119.

［9］吉國明，董萌，張量.搖臂式起落架初始設計方法研究及性能仿真［J］.科學技術與工程，2011，11（22）：5345－5349.JI Guoming，DONG Meng，ZHANG Liang.Study of early design method and Cosimulation of the performance on articulated landing gear［J］. Science Technology and Engineerin，2011，11（22）：5345－5349.

［10］魏小輝.飛機起落架著陸動力學分析及減震技術研究［D］.南京：南京航空航天大學，2005.

［11］Stefania G，Marco M，Gian L G.Antiskid induced aircraft landing gear instability［J］. Aerospace Science and Technology，2008，12：627－637.

［12］諸德培.擺振理論及防擺措施［M］.北京：國防工業出版社，1984：25－70.