地震載荷作用下岸橋結構單參數畸變相似模型研究

李 哲，胡吉全，王 東

（武漢理工大學 物流工程學院，武漢 430063）

岸橋結構大型化使其更易遭受地震破壞，明確岸橋結構地震載荷作用下的破壞模式及破壞機理，提高岸橋結構抗震性能，為大型起重設備設計及安全使用急需解決之問題［1］。

岸橋結構龐大以致無法對實際結構進行抗震試驗。模型試驗可填補此振動試驗空白。采用適當材料制作與實際結構幾何相似、按一定比例縮小的模型（縮尺模型）在振動臺上進行地震模擬試驗，測量試驗數據并按比尺換算，所得結果能近似反映實際結構地震時的動態特性。據動力相似理論設計合理的縮尺模型對研究岸橋抗震性能很有意義。實際操作中相似條件通常不能完全滿足，如梁截面厚度不能與梁長度、寬度按相同比例縮小（岸橋結構中實際梁截面厚度多為10 mm，若外形尺寸相似比為15，則模型中梁截面厚度為0.67 mm，梁主要由標準角鋼焊接而成，在實際工程中不可能達成），設計模型與原型不能完全相似，會出現畸變。畸變模型的試驗結果或數值結果無法據相似條件推廣到原型，即無法通過畸變模型預測原型的動態特性。梁架結構縮比模型設計中，為應對某些參數不能按相似比變化，采用截面慣性半徑相似實現截面彎曲剛度相似［2］，使彎曲梁構件截面慣性半徑誤差達到最小。據截面厚度設計規定，結合梁截面慣性矩公式求解模型梁截面參數；基于工程實際經驗確定梁截面厚度、長度、寬度，設計出1：50的岸橋縮尺模型。文獻［3－4］基于動力相似理論建造的1：20岸橋縮尺模型，采用質量補償法應對梁截面厚度不能按相似比變化問題，進行振動臺地震試驗并取得較好結果。

諸多基于Euler梁彎曲理論進行相似比推導中，梁厚按設計規定取值而非按相似比縮放。如僅考慮梁截面的彎曲剛度而忽視因截面厚度不同產生的質量差異及外形尺寸對位移加速度影響［2］；文獻［3－4］據動力相似原則對模型進行質量補償，將質量塊附加在模型上，附加質量取值及位置主要據經驗及計算所得定性研究結果，對安放質量塊處產生的局部應力加大及剛度均未計及。以上研究均未建立試驗或數值模型對梁截面不同厚度取值與整體結構所受地震荷載響應間關系進行定量計算。文獻［5］用畸變模型實驗，對四種艦船縮尺實驗方案進行水下爆炸數值計算分析，并總結實際模型橫剖面彎矩預測偏差。文獻［6］據有限元預測系數法對單參數產生畸變的船體相似模型進行爆炸沖擊響應研究，用數值試驗預測畸變模型的動態響應畸變系數，實現預測原模型動態特性。而畸變模型研究均無實體試驗，僅采取數值計算分析研究缺乏試驗驗證。

本文采用限元預測系數法，對岸橋起重機進行數值建模計算，并對梁截面厚度產生畸變模型進行動態響應畸變系數預測。用振動臺對截面厚度畸變的實體模型試驗分析，將模型試驗結果按相似系數推出原型反應值并與原型數值計算結果比較，以此驗證畸變預測系數在模型試驗中應用的可靠性。

1 模型相似比尺分析

本文研究對象為長66 m、高33 m、總重520 t的集裝箱岸橋。據振動臺面大小（1.5 m×1.5 m）及最大搭載質量（2 t），用1：15進行縮尺模型設計。岸橋主要由門架結構（主要包括海陸側立柱、海陸側上橫梁、海陸側下橫梁及門框橫梁）、前后大梁、前后拉桿等組成，見圖1。岸橋金屬結構材料取 Q345鋼，彈性模量206 GPa，泊松比 0.3，密度 7850 kg／m3。

圖1 集裝箱岸橋結構模型Fig.1 Structural model of the quayside container crane

1.1 結構動力模型相似量綱分析

振動問題中結構彈塑性力學性能為表征結構變形、位移及破壞的重要指標［7］。相似模型試驗中選彈性模量E、幾何尺寸l、密度ρ、時間t、動應力σ、位移u、速度v、加速度a、重力加速度g及固有頻率ω作為結構參量，通過量綱分析法確定各參量間關系。線彈性范圍內，物理量的一般函數形式［8］為

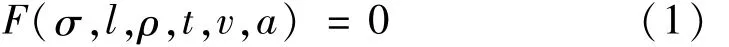
用C代表原形與模型間參量的相似比，取幾何比尺Ck＝15，模型材料與原形相同均用Q345鋼，將幾何比尺、密度比尺Cρ＝1及彈性模量比尺CE＝1作為基本比尺。由于試驗研究為岸橋主要構件梁的彎曲，故本文基于Euler梁彎曲理論推導其它相似比尺，如時間比尺Ct、頻率比尺Cω、質量比尺Cm、位移比尺Cu、速度比尺Cv、加速度比尺Ca、應變比尺Cε及應力比尺Cσ等。梁彎曲平衡條件為

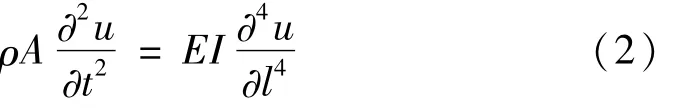
式中：A，I為梁截面積及慣性矩。

據量綱分析可得相似條件為

質量比尺 Cm＝CρCACl，位移比尺 Cu＝Cl，速度與加速度為位移對時間的一、二階微分，即

據梁彎曲應變計算公式（距離中性層為y處Cy≈Cl＝15）及胡克定律可得彈性階段應力與應變的相似關系為

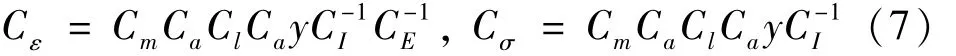
1.2 畸變模型

岸橋結構主梁為箱形梁，以海測立柱為例見圖2，梁截面寬度L、高度 H、厚度d，縮尺模型梁截面寬度Lm、高度 Hm、厚度 dm。當 Lm＝L／15，Hm＝H／15，dm＝d／15時，梁的截面積比尺為 CA＝152，截面慣性矩比尺為CI＝154。推導的岸橋原型結構與1：15縮尺模型間詳細比尺見表1。

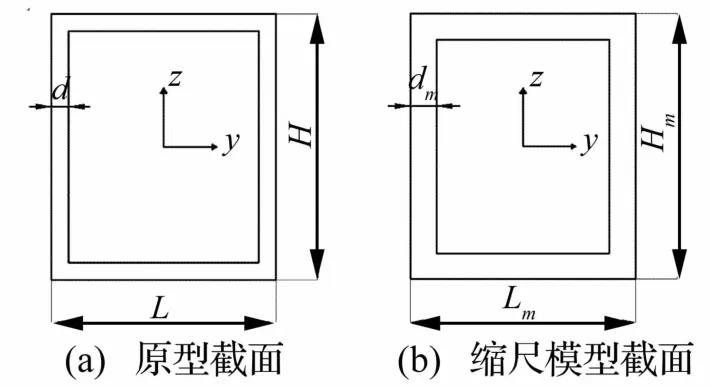
圖2 岸橋結構原型梁截面與縮尺模型梁截面Fig.2 Crosssectional shapes of bending beam components of prototype and scale mode

表1 岸橋相似模型相似關系Tab.1 Similarity relation of the scale model

模型制作過程中梁截面厚度不能與梁長、寬同比例縮小，即dm≠d／15，模型產生畸變，由π定理知模型自變項≠（πb為畸變模型值，πm為原型值），致使模型中各因變項π值不相等，畸變模型特性不能反映原模型特性。

當≠時，定義λ為畸變系數（即模型中某自變項不能按整體相似比變化產生的實際值與預計值間的比例系數），令

其它相似條件不變，以一因變為例，定義加速度預測系數 δa＝／，而與的表達式只在 πd上不同，故加速度預測系數δa為畸變系數λ的函數，且與非畸變項無關系。δa與λ間變化規律只能通過試驗或數值計算獲得經驗公式。

2 畸變預測系數

2.1 數值計算模型

為預測梁厚度畸變預測系數對岸橋按原尺寸建立足尺數值模型，見圖3。模型中海側立柱、路側立柱、上下橫梁、前后大梁均采用Beam44單元；前后大梁間鉸接及拉桿與上橫梁、前大梁間鉸接均由節點自由度耦合模擬；4立柱底端與地面剛性連接（自由度全耦合，試驗臺與相似模型即為此連接方式）；地震載荷直接由4立柱底端（用加速度或位移時程）輸入，與振動臺輸入一致。

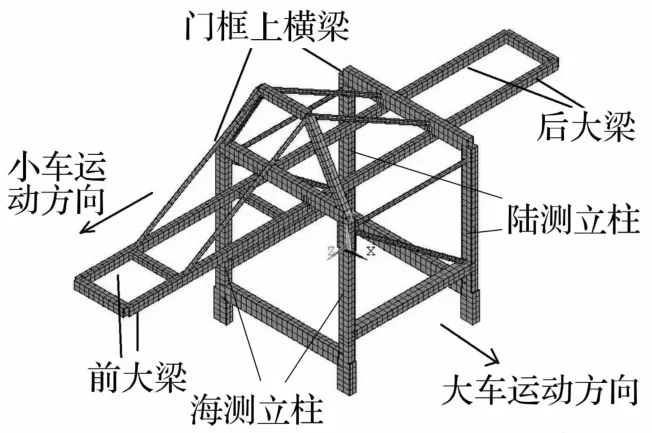
圖3 集裝箱起重機有限元模型Fig.3 Finite element model of the container crane

文獻［9］用有限元數值分析法對水下結構模態、耦合振動響應、輻射聲場相似性進行數值驗證并取得較好結果。以1：15比例建立相似基準模型（梁單元長寬高及厚度均按1∶15），在此基礎上建立一系列厚度畸變數值模型。海測立柱的畸變數據見表2（只列出寬度值，原型寬900 mm，長寬高均按1∶15縮小，岸橋結構中部分梁厚在x、z向不一致，此處選海測立柱因其梁厚度在x、z向一致均為10 mm，可使表格更簡潔明了）。

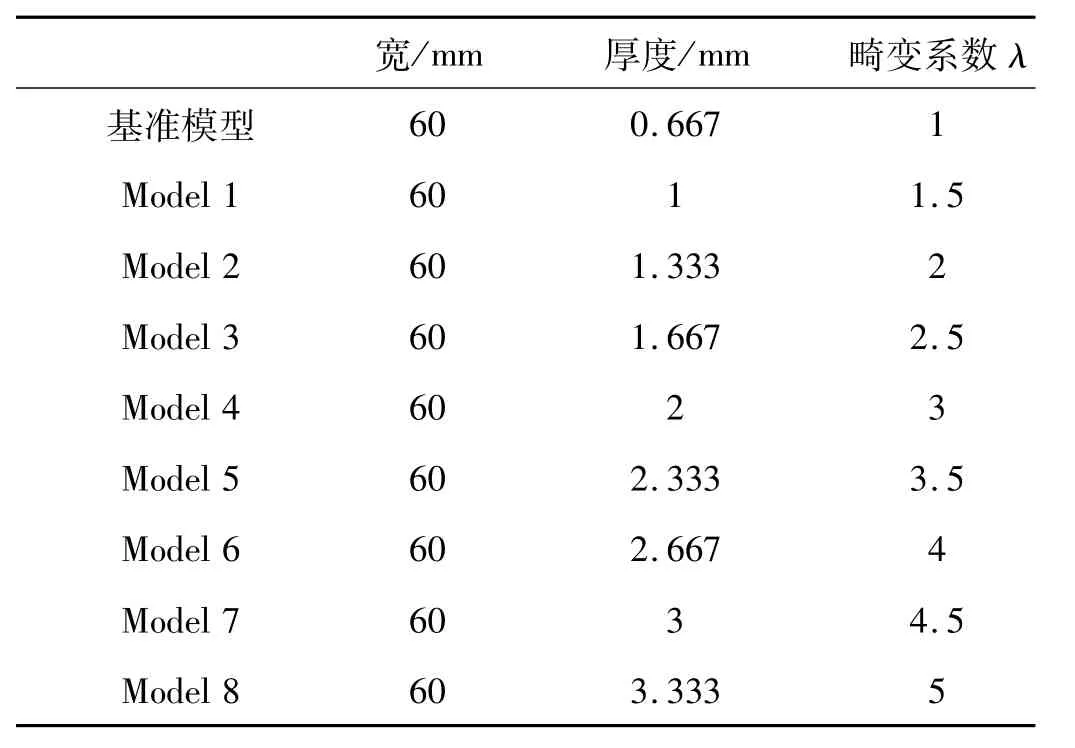
表2 基準模型與畸變模型海測立柱數據Tab.2 Data of reference model and distortion model

2.2 畸變模型預測系數

計算表2中各模型固有頻率，所得各畸變模型固有頻率預測系數δω見表3。

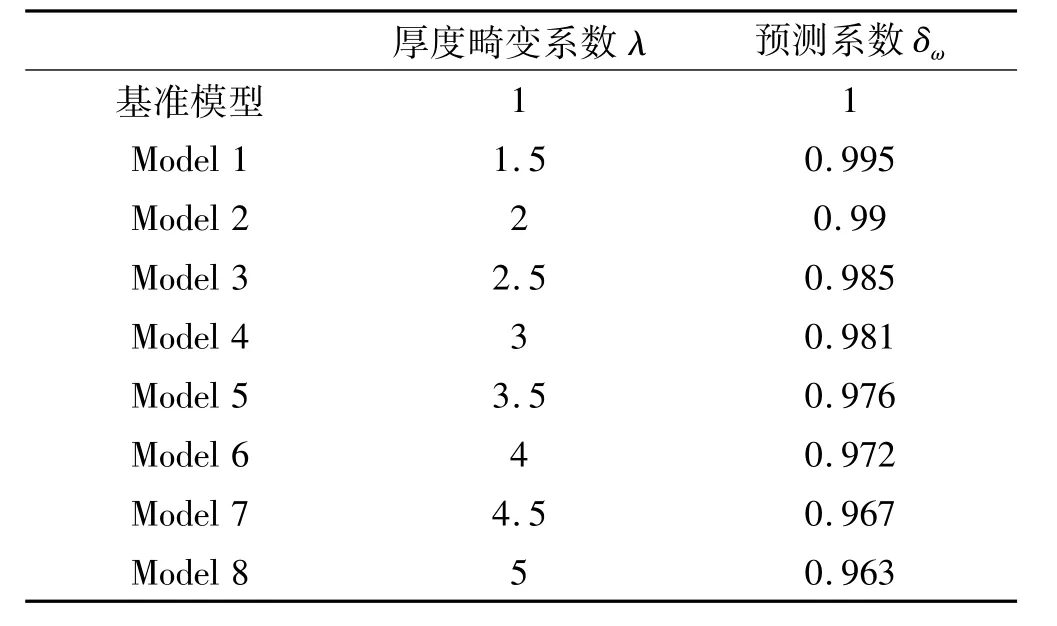
表3 固有頻率預測系數δωTab.3 Natural frequencies prediction coefficients

將表3中數據進行曲線擬合所得δω與厚度畸變系數λ的函數關系式為

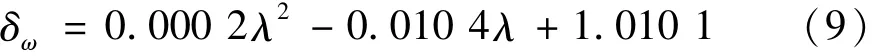
由表3看出，厚度變化時（厚度遠小于截面長寬）模型固有頻率變化較小。用對模型進行驗算證明預測系數的正確性。圖2梁的質量m＝［LH－（L－2d）（H－2d）］／ρ，梁彎曲剛度 k＝EI，梁截面剛度設截面厚度變為原型的n倍，則畸變模型質量mb＝［LH－（L－2nd）（H－0.667 mm代入，分別取 n＝3、n＝4.5，得 δ＝0.980 5、δ＝0.966 4，可認為 δ≈δω，固有頻率預測系數正確。

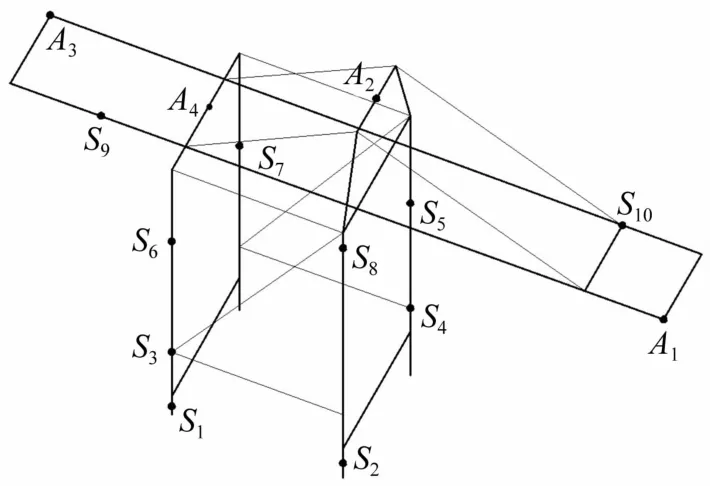
圖4 模型測量點Fig.4 Measurement nodes of the model

選A1～A4為加速度、位移考察點，S1～S10為應力應變考察點，見圖4。選EL－Centro南北向地震加速度記錄（20 s，Δt＝0.02 s）作為模型的激勵輸入，有限元計算各時程曲線均由1 000個輸出點組成。以A1點加速度時程曲線為例，取基準模型曲線的特征點a（本文取幾處峰值最大點），設基準模型在a點坐標為（ta，aa）；取畸變模型對應的特征點b，設畸變模型在b點坐標為（tb，ab），得時間預測系數 δt＝tb／ta及加速度預測系數δa＝ab／aa。將畸變模型時程曲線各點橫坐標t按時間預測系數δt縮放，將各點縱坐標按加速度預測系數δa縮放即得處理后的時程曲線。由計算所得8個頻率預測系數δω可知各時間預測系數差別較小，可忽略不計。用本文方法所得加速度預測系數δa與厚度畸變系數λ的函數關系為

位移預測系數δu與λ的函數關系為

應力預測系數δσ與λ的函數關系為

岸橋原型與畸變縮尺模型（λ＝3，厚度d＝2 mm）在地震激勵下A1點加速度、S5點應力時程曲線（實線為原型，虛線為畸變縮尺模型）見圖5、圖6。圖中原模型時間、加速度及應力已按表1相似比尺轉換，畸變模型曲線已按預測系數轉換）。由圖5、圖6對比看出，由畸變縮比模型計算所得地震響應與原型結果較接近，表明畸變預測系數的數值計算合理。

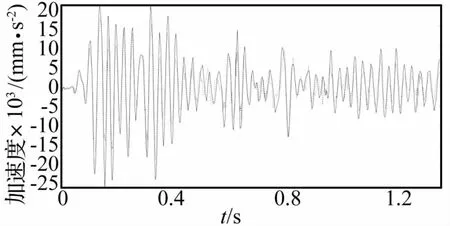
圖5 A1點加速度時程曲線Fig.5 Acceleration time history curve at A1

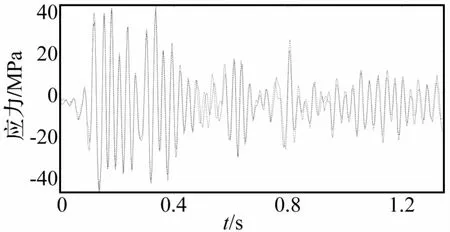
圖6 S5點應力時程曲線Fig.6 Stress time history curve at S5

為驗證式（9）～式（12）的通用性及樣本數量是否足夠、分布是否合理，用除表2、3之外的8組不同系數進行有限元建模計算并代入式（9）～式（12）對所得結果進行對比。取厚度畸變系數 1.3、1.8、2.3、2.8、3.3、3.8、4.3、4.8，所得函數關系與以上函數關系對比見圖7～圖10。其中系列1為上述計算所得函數關系，系列2為驗證所得函數關系。由圖7～圖10看出，系列1，2函數曲線近似重合，說明文中取前、后8組厚度畸變系數分布合理、樣本數量足夠。

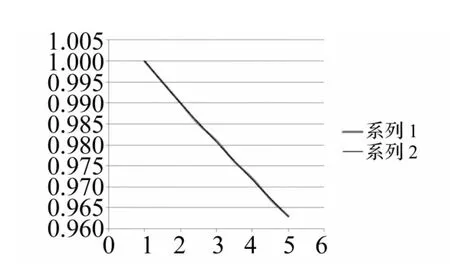
圖7 頻率系列對比Fig.7 Frequency contrast

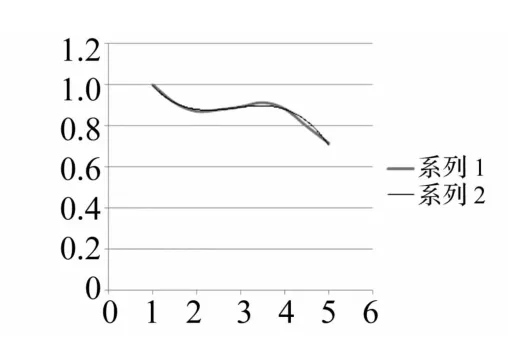
圖8 加速度系列對比Fig.8 Acceleration contrast

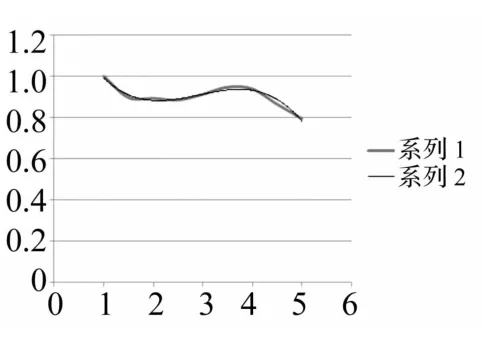
圖9 位移系列對比Fig.9 Displacement contrast

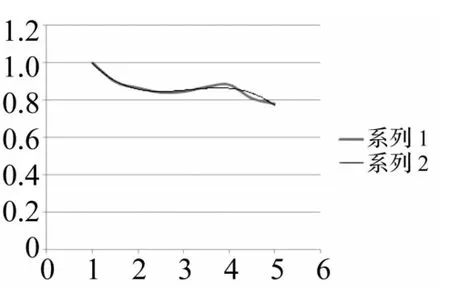
圖10 應力系列對比Fig.10 Stress contrast

數值計算中所有參數均統一標準，基準模型與一系列厚度畸變模型中除厚度按畸變系數變化外其它參數保持不變。在振動試驗中試驗模型的梁截面厚度按畸變系數變為基準厚度的3倍，其它參數不變，以此保證試驗研究的嚴謹。

3 岸橋縮尺模型試驗分析

利用實驗室畸變縮尺模型進行振動臺試驗驗證岸橋結構畸變系數的有效性，此試驗模型幾何相似常數為1：15，畸變系數 λ＝3，即板厚 d＝2 mm，見圖11。

圖11 試驗現場圖Fig.11 Test on site

3.1 錘擊模態試驗

用錘擊模態法獲取岸橋1：15縮比模型的固有頻率。采用有效獨立的改進傳感器優化布置方法［10］，在縮尺模型的前、后大梁及門架處分別布設47個單向加速度傳感器獲取加速度響應，數據直接保存至動態采集儀ECON。用N－Modal5.0進行模態分析。原型有限元模態計算結果與岸橋畸變縮尺模型模態試驗所得前6階固有頻率及相應誤差見表4（誤差為試驗值經相似比及預測系數轉換后與原型值之比）。由表4可見，畸變縮尺模型能準確預測原型結構的動態特性，且誤差較小。由此頻率畸變預測系數的正確性在試驗中得以驗證。

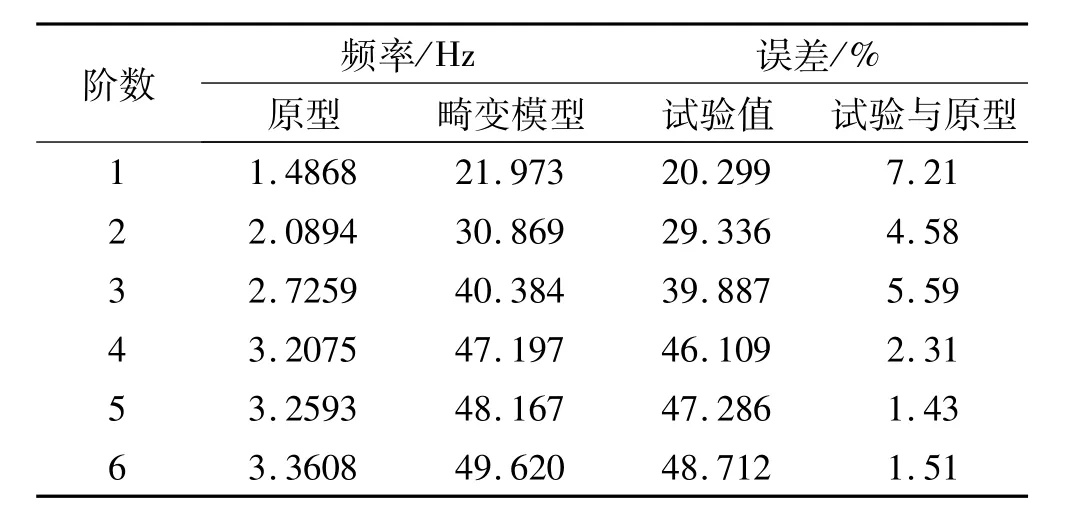
表4 原型與畸變縮尺模型固有頻率Tab.4 Natural frequencies of the prototype model and the distortion model

3.2 地震振動臺試驗

為驗證畸變預測系數的正確性，除需驗證模型在頻域內的動態特性外還需驗證模型在整個時域范圍內的變化特性。通過振動臺試驗獲取模型在地震激勵作用下的動態響應，并與原型結構有限元計算結果對比。試驗地為武漢理工大學交通部重點實驗室，振動臺驅動為電氣伺服電機式，可實施水平及垂直方向任意振動試驗，主要參數為：臺面尺寸1 500 mm×1 500 mm，水平方向最大加速度±50 m／s2，豎直方向最大加速度±30 m／s2，水平方向最大位移±200 mm，豎直方向最大位移±100 mm，水平與豎直方向最大速度均為0.8 m／s，最大承載力 2 t，頻率范圍 0.1～100 Hz，3 dB帶寬。試驗中4個加速度傳感器、10個應變片（S1～S10）安裝于模型門架結構的不同位置（圖4）。

對縮尺模型而言，基于 Ct＝15，Ca＝1／15，地震載荷時間軸被調整為原型的1／15，加速度峰值被調整為原型的15倍。處理后地震波時間較短，試驗過程相對較快，數據采集時可將數據采集系統的采樣頻率調整高些。限于篇幅，只給出考察點A1的加速度時程曲線及考察點S5的應變時程曲線，見圖12、圖13。不同測點最大動態應變見表5。由兩圖看出，1：15畸變縮尺模型能較好預測原型結構的整體地震行為。兩圖中曲線包括原型計算值與縮尺模型試驗值，其中試驗值曲線有四邊形標記，原型值已經相似轉換，試驗值已經預測系數處理。觀察圖12、13及表5知，試驗結果與有限元計算結果有一定誤差，但在地震載荷下考察點加速度、應變出現極值大小及對應時間均較近似。最大加速度出現在岸橋前大梁前端與后大梁尾端，與試驗結果一致，符合實際地震情況下岸橋結構加速度響應。

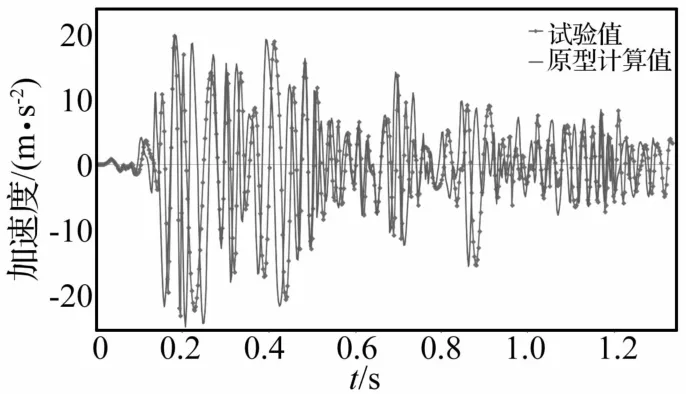
圖12 A1點加速度時程曲線Fig.12 Acceleration time history curve at A1

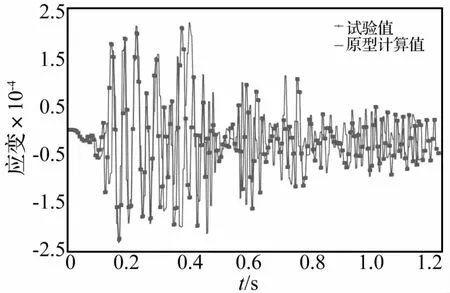
圖13 S5點應變時程曲線Fig.13 Strain time history curve at S5

最大應變主要集中在陸側立柱中上部及海側立柱上部，與測量結果完全一致。原型結構應變分布與表5應變分布基本一致，說明采用厚度產生畸變的縮比模型亦能獲得較合理的試驗數據。

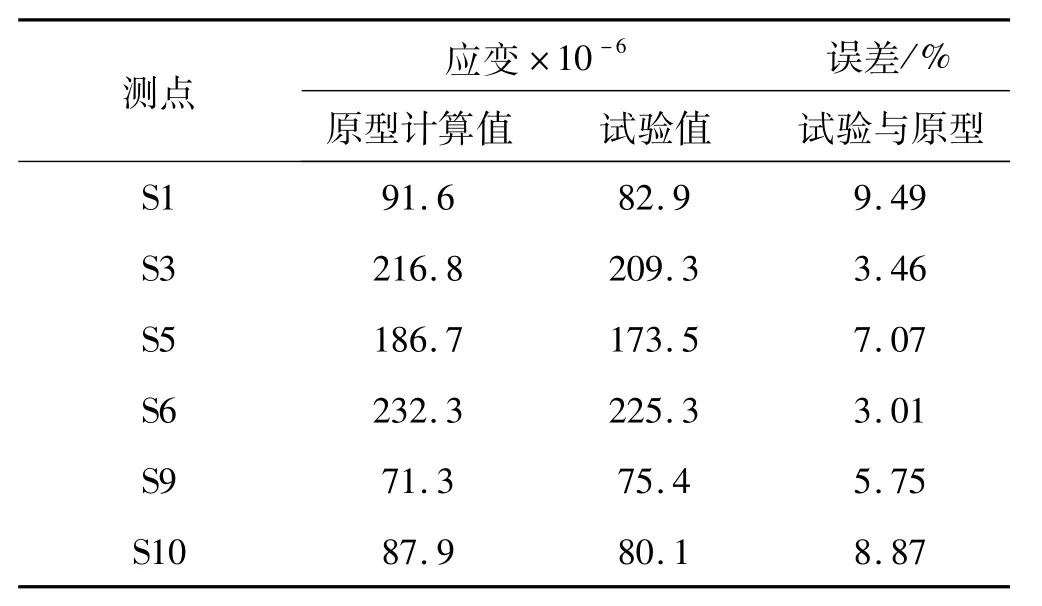
表5 不同測點最大動態應變Tab.5 Maximum dynamic strain at various nodes

結果差異原因主要為：① 有限元模型建立中存在簡化部分；② 相似比例主要據Euler梁彎曲理論推導，而實際結構更復雜；③ 傳感器位置誤差及傳感器本身誤差；④ 結構振動試驗存在非線性問題，數值模型基于彈線性基礎，相似比計算在彈性范圍內；⑤ 外部環境因素影響。相對誤差在一定許可范圍內試驗結果總體與有限元計算較符合，畸變預測系數的有效性得到進一步驗證。

4 結 論

［1］李哲，王貢獻，王東，等.大型集裝箱起重機地震動力學行為試驗方法研究［J］.武漢理工大學學報，2013，35（8）：72－76.LI Zhe，WANG Gongxian，WANG Dong，et al.Testing methods on dynamics behavior of jumbo container cranes under seismic loads［J］.Journal of Wuhan University of Technology，2013，35（8）：72－76.

［2］Jin Y L，Li Z G.Theoretical design and experimental verification of a 1／50 scale model of a quayside container crane［J］.Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science，2012，226（6）：1644－1662.

［3］Jacobs L D，DesRoches R，Leon R T.Seismic behavior of a jumbo container crane including uplift［J］.Earthquake Spectra，2011，27（3）：745－773.

［4］Jacobs L D，DesRoches R，Leon R T.Experimental study of the seismic response of container cranes［C］.Ports 2010：Building on the Past，Respecting the Future 210 Don’t Mess with Structural Engineers，2010：91－99.

［5］張海鵬，岳永威，蘇羅青，等.水下爆炸作用下艦船總縱強度模型實驗方案研究［J］.振動與沖擊，2012，31（6）：175－180.ZHANG Haipeng，YUE Yongwei，SU Louqing，et al.Model experimental scheme for longitudinal strength of a warship subjected to underwater explosion［J］.Journal of Vibration and Shock，2012，31（6）：175－180.

［6］張瑋，汪玉，杜儉業.瞬態載荷作用下船體板架結構單參數畸變響應模型研究［J］.兵工學報，2010，31（S1）：172－178.ZHANG Wei， WANG Yu， DU Jianye. Research on similarity of dynamic response of ship grillage subjected to transient load［J］.Acta Armamentarii，2010，31（S1）：172－178.

［7］何川，汪洋，方勇，等.土壓平衡式盾構掘進過程的相似模型試驗［J］.土木工程學報，2012，45（2）：162－169.HE Chuan，WANG Yang，FANG Yong，et al.Similarity model test of earthpressurebalanced shield tunneling process［J］.China Civil Engineering Journal，2012，45（2）：162－169.

［8］金玉龍，吳天行.集裝箱碼頭岸橋結構的動力相似分析與試驗驗證［J］.上海交通大學學報（自然科學版），2012，46（10）：1609－1615.JIN Yulong，WU Tianxing.Dynamic similarity analysis and experimental verification on a quayside container crane［J］.Journal of Shang Hai Jiaotong University，2012，46（10）：1609－1615.

［9］王永富，周其斗，紀綱，等.水中結構振動時聲學相似性的數值驗證［J］.振動與沖擊，2012，31（16）：66－71.WANG Yongfu，ZHOU Qidou，JI Gang，et al.Numerial investigation on acoustic similarity of fluidloaded stiffened cylinder［J］. Journal of Vibration and Shock，2012，31（16）：66－71.

［10］劉偉，高維成，李惠，等.基于有效獨立的改進傳感器優化布置方法研究［J］.振動與沖擊，2013，32（6）：54－62.LIU Wei，GAO Weicheng，LI Hui，et al.Improved optimal sensor placement methods based on effective independence［J］.Journal of Vibration and Shock，2013，32（6）：54－62.