基于時頻分析的質量慢變轉子系統非線性動力學特性研究

于 濤，王 嬌，李英杰，孫 偉，韓清凱

（1.煙臺大學 機電汽車工程學院，山東 煙臺 264005；2.山東省高校先進制造與控制技術重點實驗室，山東 煙臺 264005；3.大連理工大學 機械學院，遼寧 大連 116024）

在分離、紡織、起重、電動、發電等機械中轉子系統作為主要部件因工作環境及工況要求導致轉子質量不斷發生變化。如燃氣輪機轉子葉片受工作介質沖刷腐蝕、粘連堆積導致葉片質量發生改變；紡織機械的轉子部件質量由纏繞物的多少隨時間緩慢變化。傳統上將此類轉子系統稱質量慢變轉子系統［1－5］。而有關此類轉子系統研究較少。Cveticanin［6－7］研究質量慢變轉子系統非線性特性，包括自激振動及混沌運動等；王宗勇等［8－10］研究質量慢變轉子系統松動、碰摩故障下周期運動及擬周期運動。

本文基于漸近解析法［11－12］獲得簡化集中質量模型質量慢變轉子系統解析解，并采用重分布小波尺度圖對具體質量慢變模型進行時頻特征分析，獲得豐富的質量慢變轉子動力學行為。

1 質量慢變轉子動力學方程

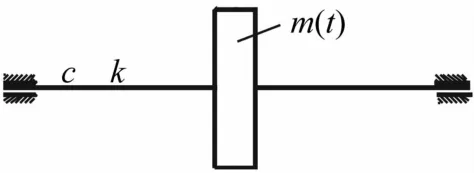
圖1 基于簡單集中質量的質量慢變Jeffcott轉子Fig.1 Simplifiedconcentratedmass based model of Jeffcott rotor system with slowlyvarying mass

圖1為Jeffecott轉子系統，其質量隨時間緩慢變化，該系統動力學方程為

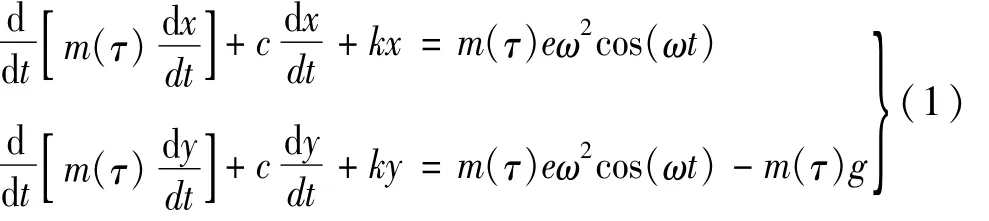
式中：m（τ）為轉子慢變質量；c為轉子系統阻尼系數；k為轉軸線性剛度系數；g為重力加速度。

通過與恒定質量轉子系統對比知，質量慢變轉子系統增加一阻尼力項，且該項阻尼系數為慢變質量的函數。若質量由小到大變化則該慢變阻尼系數為正，反之為負，會產生自激振動；質量慢變轉子系統固有頻率亦為慢變的，亦會引起振幅、相位差角的慢變。阻尼力、激振力較小時令 c／m（τ）＝2εξω0（τ），e＝εr，則式（2）可化簡為

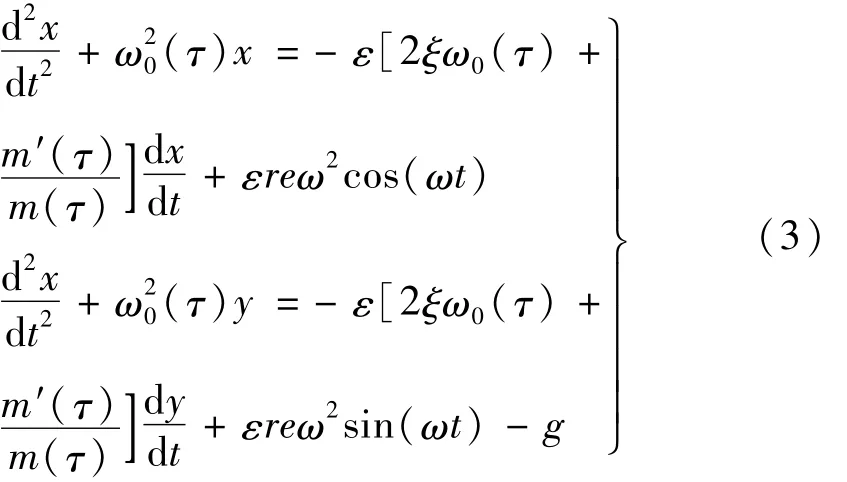
2 解析求解

由于式（3）的兩方程互不關聯可分別求解。以求解水平方向為例

式中：a，εu1（τ，a，t，ψ）為時間 t的函數。

取方程的一次近似解為

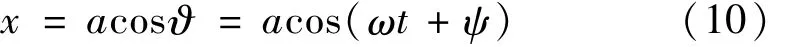
式中：a，ψ為時間t的函數，計算式為

將式（16）代入式（14），整理得

3 基于解析解的質量慢變轉子系統時頻響應小波分析

對連續操作的分離機械而言，其轉子質量可認為圍繞某一質量上下波動，波動幅度取決于物料性質，波動頻率取決于加料周期。為便于分析，令轉子的慢變質量為

式中：k＝48EI／L3，I＝πd4／64為轉軸截面通過形心的慣性矩，d＝2R為轉軸直徑。

設Jeffcott轉子模型半徑R＝10 mm，長度L＝480 mm，彈性模量 E＝2.06E11 N／m2，則轉子軸剛度 K＝43 888 N／m。令m0＝1 kg，ξ＝0.1，e＝0.000 1 m，則27 Hz＜f0＜47 Hz。采用四階Runge－Kutta法對微分方程組（20）數值求解。ωm＝100 rad／s、ε＝0.01、λ＝0.5時取慢變質量轉子系統穩態轉速ω分別為20 Hz、30 Hz、40 Hz、60 Hz，所得質量慢變轉子系統時頻響應曲線見圖2～圖11。由圖2看出，質量慢變轉子系統低于系統固有頻率穩態運轉時，系統頻率成分除工頻外在27～47 Hz范圍內出現密頻成分。

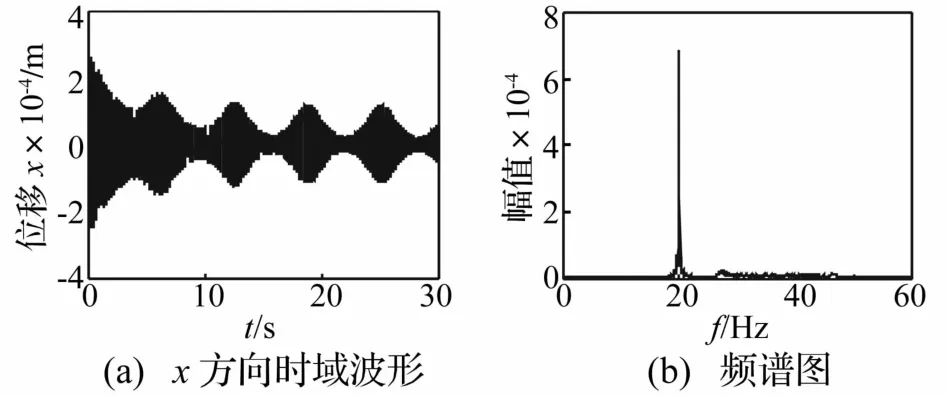
圖2 質量慢變轉子系統時頻響應曲線（ω＝20 Hz，ε＝0.01）Fig.2 Timefrequency response of rotor system with slowlyvarying mass（ω＝20 Hz，ε＝0.01）

為更清楚觀察該范圍內的頻率成分，對圖2（a）時域波形進行高通濾波、頻譜分析，所得時頻曲線見圖3。由圖3看出，系統響應經高通濾波后低頻成分消失，頻譜圖中顯示出27～47 Hz間密頻成分，但由于頻率成分過于密集無法辨認，因此對濾波后的時域信號進行小波重排尺度分析，見圖4。由圖4看出，隨時間推移，去除工頻成分的質量慢變轉子系統重排Morlet尺度圖中轉子頻率按簡諧特征波動，呈一條明顯的簡諧頻率帶，且以2π為周期，頻率幅值波動漸小。

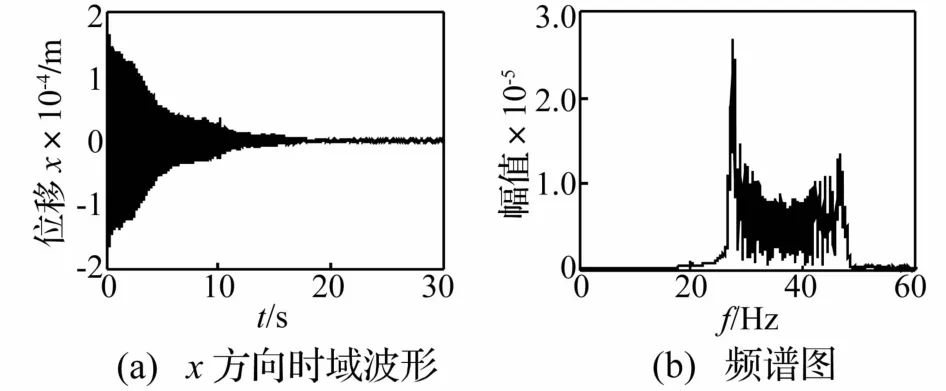
圖3 高通濾波后轉子系統時頻響應曲線（ω＝20 Hz，ε＝0.01）Fig.3 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering（ω＝20 Hz，ε＝0.01）

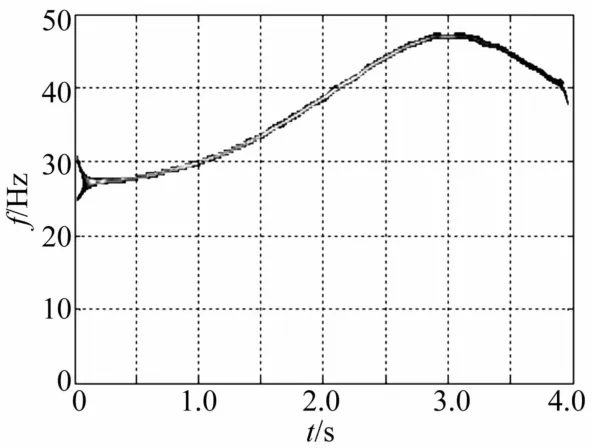
圖4 高通濾波后質量慢變轉子系統重排 Morlet尺度圖（ω＝20 Hz，ε＝0.01）Fig.4 Reassigned morlet scalograms of rotor system with slowlyvarying mass after highpass filtering（ω＝20 Hz，ε＝0.01）

質量慢變轉子系統以30 Hz、40 Hz在系統固有頻率變化范圍內穩態運轉時，其時頻響應曲線見圖5、圖7。由兩圖看出，系統存在豐富的頻率成分，對時域信號進行FFT分析時在27～47 Hz之間存在密頻成分，且轉子工頻湮沒其中。系統響應重排Morlet尺度圖見圖6、圖8。由兩圖看出，系統頻率有2π的周期波動。

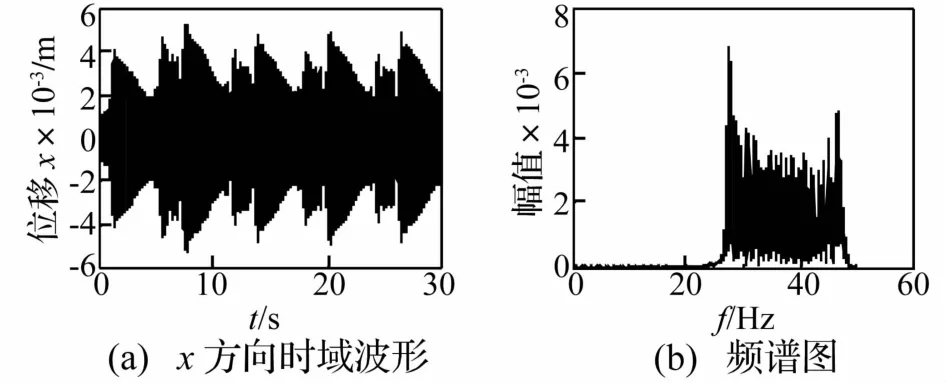
圖5 質量慢變轉子系統時頻響應曲線（ω＝30 Hz，ε＝0.01）Fig.5 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering（ω＝30 Hz，ε＝0.01）

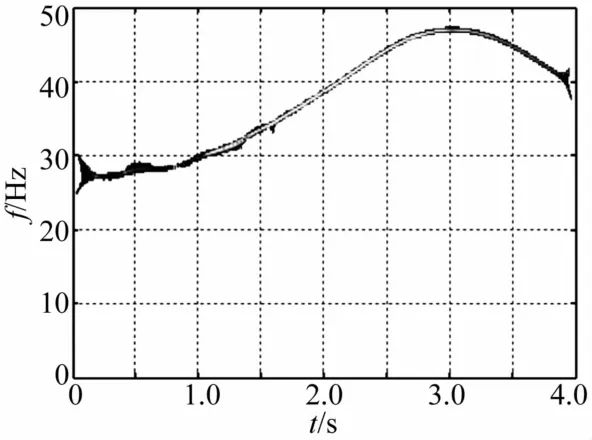
圖6 質量慢變轉子系統重排Morlet尺度圖（ω＝30 Hz，ε＝0.01）Fig.6 Reassigned Morlet scalograms of rotor system with slowlyvarying mass（ω＝30 Hz，ε＝0.01）

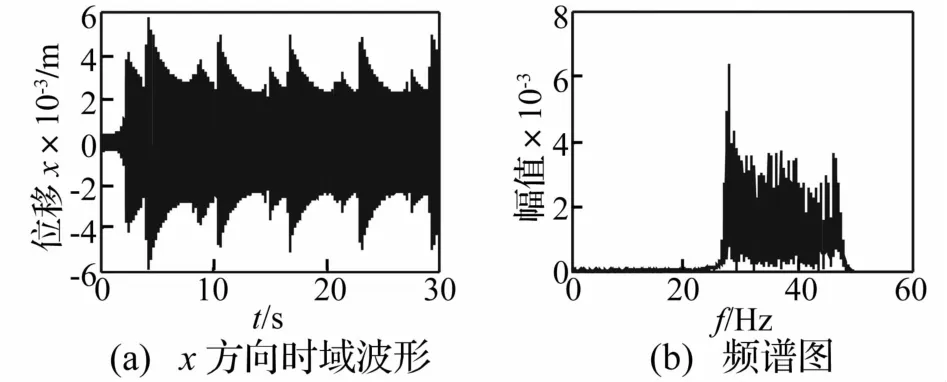
圖7 質量慢變轉子系統時頻響應曲線（ω＝40 Hz，ε＝0.01）Fig.7 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering（ω＝40 Hz，ε＝0.01）

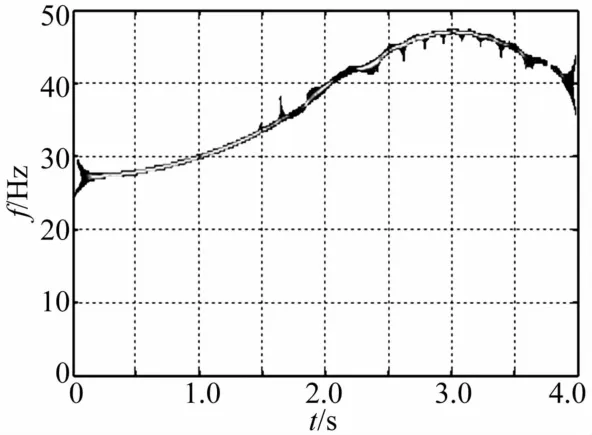
圖8 質量慢變轉子系統重排Morlet尺度圖（ω＝40 Hz，ε＝0.01）Fig.8 Reassigned Morlet scalograms of rotor system with slowlyvarying mass（ω＝40 Hz，ε＝0.01）

圖9 質量慢變轉子系統時頻響應曲線（ω＝60 Hz，ε＝0.01）Fig.9 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering（ω＝60 Hz，ε＝0.01）

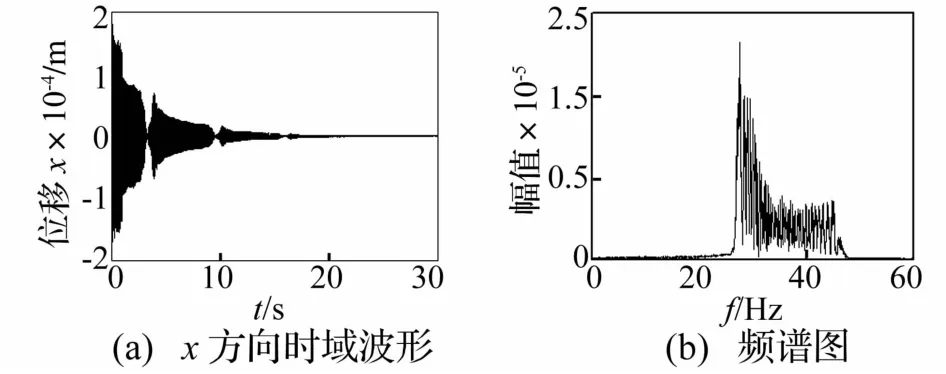
圖10 低通濾波后的轉子系統時頻響應曲線（ω＝60 Hz，ε＝0.01）Fig.10 Timefrequency response of rotor system with slowlyvarying mass after lowpass filtering（ω＝60 Hz，ε＝0.01）

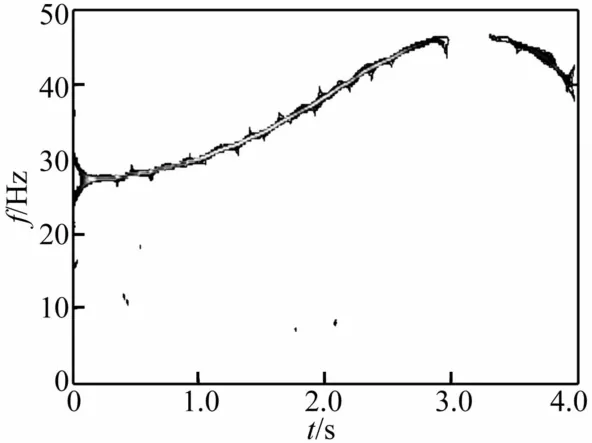
圖11 低通濾波后質量慢變轉子系統重排Morlet尺度圖（ω＝60 Hz，ε＝0.01）Fig.11 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after lowpass filtering（ω＝60 Hz，ε＝0.01）

質量慢變轉子系統以60 Hz在超系統固有頻率范圍外穩態運轉時，系統時域信號呈周期運動的時頻響應見圖9。由圖9看出，除高頻工頻外在低于工頻范圍內亦存在密頻成分。因此對時域信號進行低通濾波，濾波后慢變轉子系統時頻響應曲線見圖10。由圖10看出，低頻部分從27～47 Hz為系統固有頻率變化范圍。系統響應重排Morlet尺度圖見圖11。由圖11看出，系統低頻部分作大周期的頻率波動。

對給定參數的質量慢變轉子系統時頻響應特點，可認為在給定質量慢變模型下，系統頻率響應存在T＝2π／（ωmε）的大周期波動，頻率波動周期 T＝2π／（100×0.01）＝2π。為考察質量慢變參數ε對系統響應影響，討論 ωm＝100 rad／s、ε＝0.1、λ＝0.5時質量慢變轉子系統時頻響應。取慢變質量轉子系統穩態轉速ω分別為20 Hz、30 Hz、60 Hz時，系統時頻響應見圖12～圖19。轉速為20 Hz時系統時頻響應見圖12。由圖12看出，由于質量慢變導致系統固有頻率時變，在工頻附近出現多成分頻譜，且頻譜間相差 Δf＝ωmε／（2π）＝100×0.1／2／3.14＝1.59 Hz；在高頻區存在幅值相對較低的密頻區。對時域信號進行高通濾波的時頻圖見圖13。由圖13看出，在20～50 Hz區間以20 Hz為基準，Δf為增量的連續頻譜，系統以 T＝2π／（ωmε）＝1／Δf周期作頻率波動。

圖12 質量慢變轉子系統時頻響應曲線（ω＝20 Hz，ε＝0.1）Fig.12 Timefrequency response of rotor system with slowlyvarying mass（ω＝20 Hz，ε＝0.1）

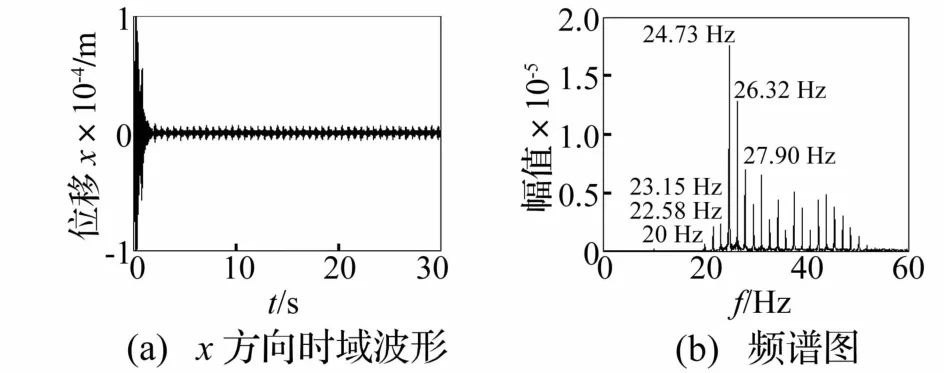
圖13 高通濾波后質量慢變轉子系統時頻響應曲線（ω＝20 Hz，ε＝0.1）Fig.13 Timefrequency response of rotor system with slowlyvarying mass after highpass filtering

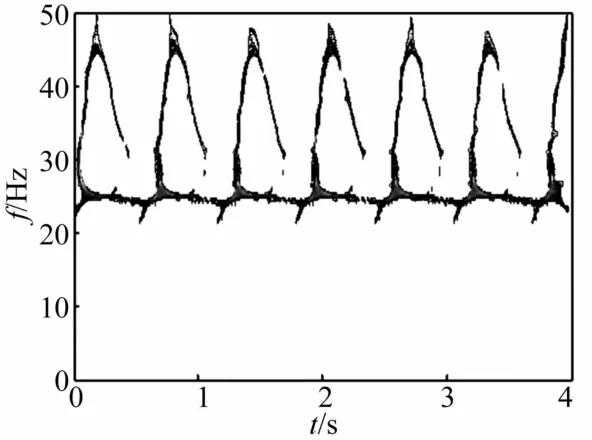
圖14 高通濾波后質量慢變轉子系統重排Morlet尺度圖（ω＝20 Hz，ε＝0.1）Fig.14 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after highpass filtering

質量慢變轉子系統以穩態轉速在30 Hz運轉時，系統響應見圖15、圖16。由兩圖看出，系統穩定運轉在固有頻率變化范圍內時，在共振區及附近以工頻為基準Δf為增量，出現豐富的頻率成分，且系統頻率隨時間的推移以 T＝2π／（ωmε）＝1／Δf周期作頻率波動。

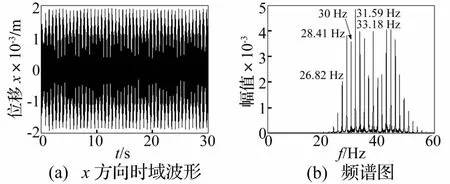
圖15 質量慢變轉子系統時頻響應曲線（ω＝30 Hz，ε＝0.1）Fig.15 Timefrequency response of rotor system with slowlyvarying mass

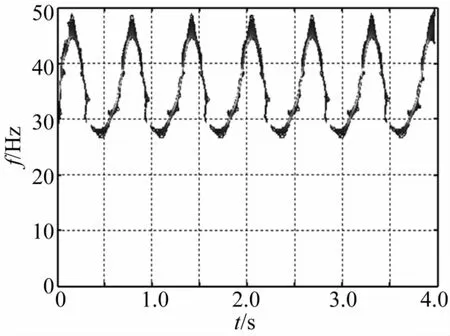
圖16 質量慢變轉子系統重排Morlet尺度圖（ω＝30 Hz，ε＝0.1）Fig.16 Reassigned Morlet scalograms of rotor system with slowlyvarying mass

圖17 質量慢變轉子系統時頻響應曲線（ω＝60 Hz，ε＝0.1）Fig.17 Timefrequency response of rotor system with slowlyvarying mass

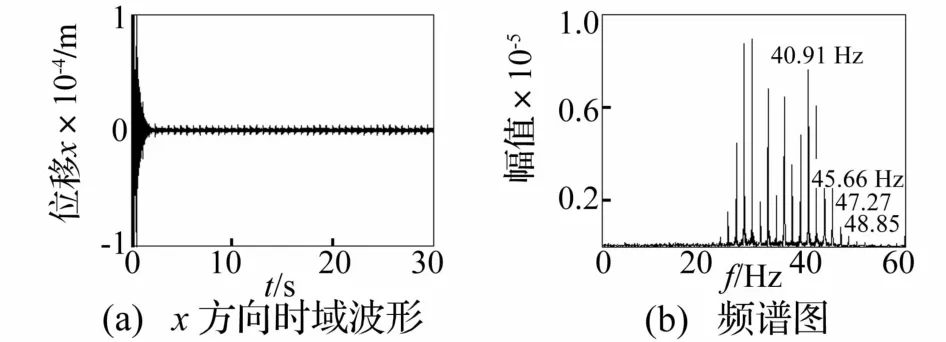
圖18 低通濾波后質量慢變轉子系統時頻響應曲線（ω＝60 Hz，ε＝0.1）Fig.18 Timefrequency response of rotor system with slowlyvarying mass after lowpass filtering

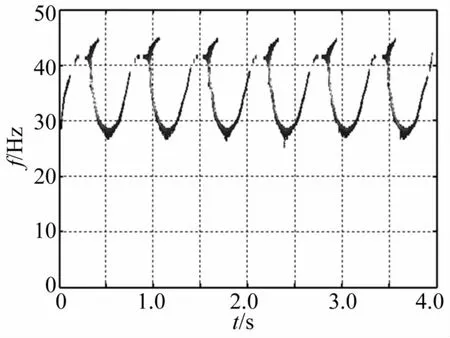
圖19 低通濾波后質量慢變轉子系統重排Morlet尺度圖（ω＝60 Hz，ε＝0.1）Fig.19 Reassigned Morlet scalograms of rotor system with slowlyvarying mass after lowpass filtering

慢變質量轉子系統以穩態轉速在60 Hz運轉時系統時頻響應見圖17。由圖17看出，系統呈現與低于臨界轉速運轉時的系統響應相似特點。因此對質量慢變模型 m（τ）＝m0（1＋λcos（ωmτ））而言，系統頻率響應與ωm及 ε的乘積有關，即系統作周期為 T＝2 π／（ωmε）的頻率波動，頻率成分隨時間推移以工頻轉速為基準、Δf＝ωmε／（2π）為增量進行簡諧波動。

4 結 論

本文基于漸近法，給出質量慢變轉子系統解析分析方法，推導出質量慢變轉子系統響應的解析解，研究、討論具有單一質量慢變模型的轉子系統非線性動力學響應，結論如下：

（1）質量慢變導致系統固有頻率產生時變，系統頻率響應與ωm，ε的乘積有關，且頻率成分隨時間推移以工頻轉速為基準、以T＝2π／（ωmε）為增量進行簡諧波動。

（2）基于漸近方法的質量慢變轉子系統響應解析解的一次近似解，對精度、分辨率而言已足夠。

［1］聞邦椿，顧家柳，夏松波，等.高等轉子動力學－理論、技術與應用［M］.北京：機械工業出版社，2000.

［2］李以農，鄭玲，聞邦椿.一類具有參數慢變的非線性振動系統［J］.重慶大學學報，2000，23（6）：16－18.LI Yinong，ZHENG Ling，WEN Bangchun.Study on the nonlinear vibration system with slowchanging parameters［J］.Journal of Chongqing University，2000，23（6）：16－18.

［3］米特洛波利斯基ЮА，著.吳滄浦，譯.非線性振動系統中的不平穩過程［M］.北京：科學出版社，1958.

［4］韓清凱，劉杰，聞邦椿.不對稱滯回模型的一般形式及其參數慢變特性［J］.振動與沖擊，2000，19（3）：14－16.HAN Qingkai， LIU Jie， WEN Bangchun. General formulations of asymmetrical hysteretic models and the slowlyvarying characteristics of their parameters［J］.Journal of Vibration and Shock，2000，19（3）：14－16.

［5］于濤.損傷轉子動力學及其故障診斷若干關鍵問題研究［D］.沈陽：東北大學，2007.

［6］Cveticanin L.Chaos in rotors with slowly varying mass［J］.Journal of Sound and Vibration，1995，185（5）：897－901.

［7］Cveticanin L.Normal mode of vibration for continuous rotors with slow time variable mass［J］.Mech.Mach.Theory，1997，32（7）：881－891.

［8］王宗勇，吳敬東，聞邦椿.質量慢變轉子－滾動軸承系統的支承松動故障分析［J］.中國機械工程 2005，16（13）：1197－1200.WANG Zongyong，WU Jingdong，WEN Bangchun.Study on pedestal looseness faults of a rotorroll bearing system with slowly varying mass［J］.China Mechanical Engineering，2005，16（13）：1197－1200.

［9］王宗勇，龔斌，聞邦椿.激勵幅值慢變轉子系統的動力學研究［J］.中國機械工程，2007，18（24）：2969－2973.WANG Zongyong，GONG Bin，WEN Bangchun.Study on dynamics of rotor systems with slowly varying excitation magnitude［J］.China Mechanical Engineering，2007，18（24）：2969－2973.

［10］王宗勇.參數慢變轉子系統動力學及其故障研究［D］.沈陽：東北大學，2004.

［11］包戈留包夫НЯ，米特洛列斯基A，著.金福臨，譯.非線性振動理論的漸近方法［M］.北京：科學出版社，1961.

［12］于海，陳予恕，曹慶杰.多自由度裂紋轉子系統非線性動力學特性分析［J］.振動與沖擊，2014，33（7）：92－98.YU Hai，CHEN Yushu，CAO Qingjie.Nonlinear dynamic behavior analysis for a cracked multiDOF rotor system［J］.Journal of Vibration and Shock，2014，33（7）：92－98.