基于趨勢分析的AMDF基音檢測改進算法

宗 源，曾毓敏，張 夢，李鵬程

（南京師范大學 物理科學與技術學院，南京 210023）

基音作為語音信號處理的重要特征參數，指人在發濁音時氣流通過聲門使聲帶張弛振蕩的振動頻率（或周期），廣泛用于語音編碼、語音合成、語音增強及語音識別等。因此能準確檢測基音意義極其重要。經典的基音檢測算法有自相關函數法［1］、平均幅度差函數 法 （Average Magnitude Difference Function，AMDF）［2］、倒譜法［3］及小波變換法［4］等。盡管已有諸多算法及其改進算法，但準確、可信的基音檢測算法研究仍為具有挑戰性工作［5］。

AMDF算法以原理簡單、計算復雜度低等優點得以廣泛使用。由AMDF定義知，周期信號或準周期信號將在AMDF時延等于信號周期處會產生極小值（谷值點）。濁音語音信號因具有準周期性，因此可通過計算短時窗內語音信號的AMDF，并據AMDF除零點外的最低谷值點估計語音信號基音；但該最低谷值點的選擇受共振峰效應、語音信號并不嚴格的準周期性、噪聲等諸多因素干擾［6］，使AMDF在檢測過程中易發生倍頻錯誤，即檢測結果為實際基音的N倍。分析AMDF發現，隨時延的增加計算AMDF語音幀的重疊部分會逐漸減少，導致AMDF波形呈均值下降趨勢（falling trend）［7］，且使AMDF非基音谷值點有時低于實際基音谷值點而發生檢測錯誤。

為克服此下降趨勢，文獻［7］提出改進的AMDF函數，稱為 Circular AMDF（CAMDF）。CAMDF通過改變傳統的AMDF計算方法克服均值下降趨勢，檢測效果較好；文獻［8］提出的 Extended AMDF（EAMDF）可補償隨時延增加而減少的語音幀重疊部分達到去除下降趨勢效果。這些改進算法雖能克服均值下降趨勢，但均通過改變AMDF定義或改變語音幀長達到目的，因此仍會帶來無法預估的錯誤，并不能從根本上解決均值下降趨勢所致AMDF算法出現倍頻錯誤問題。

本文由時間序列分析角度對AMDF進行分析，提出基于去均值下降趨勢的AMDF基音檢測算法改進框架。該框架完全不同于以CAMDF與EAMDF為代表的兩類AMDF改進算法，主要將AMDF視為一段時間序列，利用趨勢分析方法提取AMDF序列的均值下降趨勢；將均值下降趨勢從AMDF中減去獲得改進的AMDF用于檢測基音。在該改進框架下提出以線性趨勢表示AMDF的均值下降趨勢，得到改進的AMDF（本文定義為LSAMDF）。仿真實驗結果表明，LSAMDF能較好克服傳統AMDF的倍頻檢測錯誤，且算法復雜度較低。

1 傳統AMDF及改進算法分析

語音信號的短時平均幅度差函數定義為

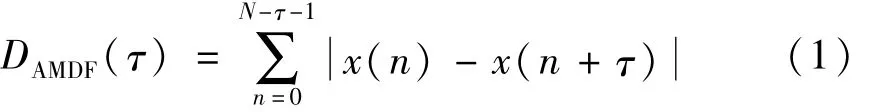
式中：x（n）為加窗長為N的矩形窗濁音語音幀；τ為時延。

DAMDF（τ）擁有與濁音語音一致的周期特性，并在τ＝Fs／Fp處出現最小谷值（除零點外）。其中Fp為基音頻率；Fs為采樣頻率。通過計算DAMDF（τ）找出最小谷值點即能檢測出濁音語音基音頻率；但因為x（n）為加窗后的語音幀，窗外語音信號值均為零，故隨時延τ的增加AMDF不能完全顯示濁音語音幀的周期性本質，而均值變化呈下降趨勢，（見圖1（b），待檢測語音信號見圖1（a），采樣頻率 20 000 Hz，信號長度 512采樣點），由此導致實際應用中會出現表示真正基音點并非最小谷值。由圖1（b）看出，均值下降趨勢會直接影響AMDF性能。

解決AMDF存在問題有兩種方法：

（1）修正 AMDF定義：如 LVAMDF［9］，CAMDF等。其中CAMDF因性能突出頗受關注，其定義為

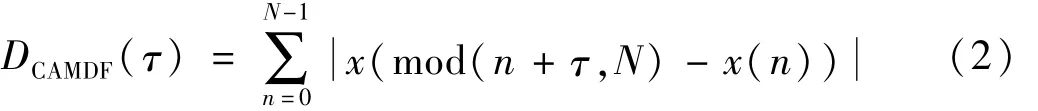
由式（2）知，CAMDF關于 τ＝N／2對稱。因此CAMDF僅前半部分有效，對基音谷值點落在AMDF后半部分的濁音語音幀，CAMDF不能準確檢測基音。由于CAMDF已改變AMDF的定義，因此會帶來未知錯誤。圖1（c）為圖1（a）濁音語音幀的 CAMDF，便發生檢測錯誤。

（2）改變用于計算AMDF的語音幀長度。EAMDF即為通過將語音幀前后各增加半幀長的語音信號，可補償隨延遲增加而引起重疊部分的減少、克服AMDF下降趨勢。EAMDF定義為

由式（3）知，實際的EAMDF計算涉及三個語音幀，即待檢測語音幀及其前后相鄰的兩個語音幀。因此盡管EAMDF能克服AMDF的下降趨勢，但EAMDF并非嚴格意義的待檢測語音幀的AMDF。而語音幀長度過長也易破壞語音幀的短時平穩性，使EAMDF會產生檢測錯誤。由圖1（d）看出，EAMDF亦發生檢測錯誤。

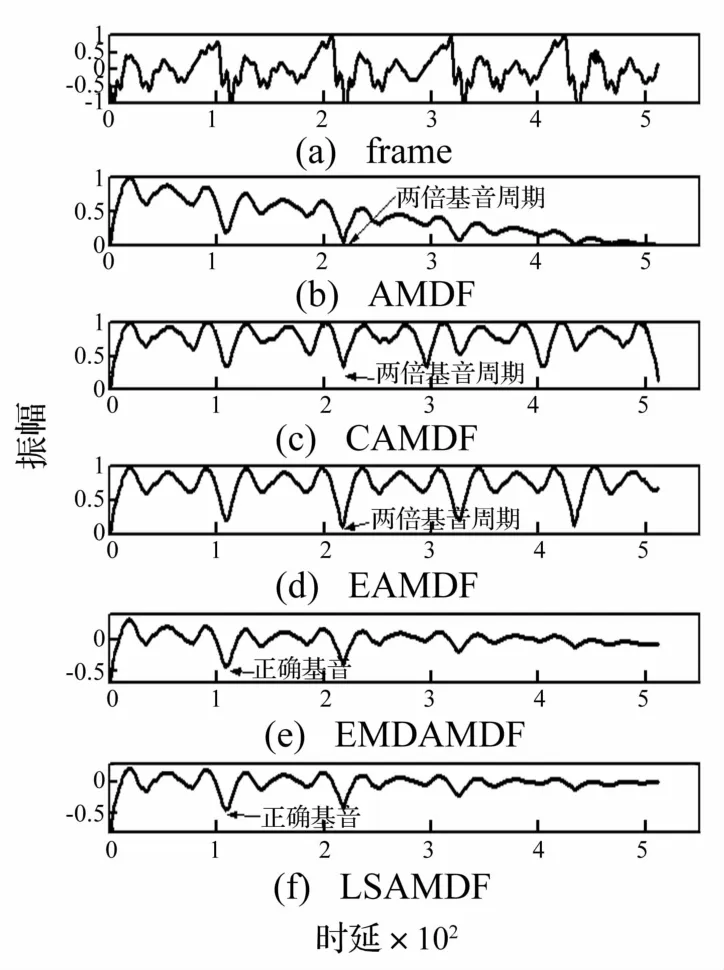
圖1 濁音語音信號AMDF、CAMDF、EAMDF，EMDAMDF與LSAMDF的比較Fig.1 Comparison between AMDF，CAMDF，EAMDF，EMDAMDF and LSAMDF on a voiced speech frame

由時間序列分析觀點，AMDF存在的均值下降趨勢即是為時間序列分析中的趨勢問題。趨勢項一直被視為時間序列長時間動向，盡管趨勢項在數學上無準確定義，但一般認為趨勢項為測試信號中周期遠大于信號記錄時間長度成分［10］。宗源等［11］利用經驗分解模式（Empirical Mode Decomposition，EMD）對 AMDF進行分析，發現殘余分量即為AMDF均值下降趨勢，利用除殘余分量外所有本征模式函數（Intrinsic Mode Functions，IMFs）重構獲得不含均值下降趨勢、改進的AMDF（定義為EMDAMDF），且檢測性能較好。在此基礎上及受文獻［12－13］啟發，本文提出改進框架克服AMDF均值下降趨勢，能從根本上解決AMDF易發生倍頻檢測錯誤問題，見圖2。該框架完全有別于以上兩種常見的AMDF改進方法框架，主要分均值下降趨勢提取及均值下降趨勢去除兩步。

由EMDAMDF原理知，EMDAMDF實際上亦可歸于此改進框架內；但EMD提取AMDF均值下降趨勢需進行多次三次樣條擬合及去除上下包絡均值操作，計算量較大。為改進AMDF，圖2的改進框架并不需要非常精確獲得AMDF的均值下降趨勢。因此本文提出利用線性多項式表示AMDF的均值下降趨勢。在此基礎上即可通過最小二乘法擬合均值下降趨勢，獲得改進的 AMDFLSAMDF（Least squarebased AMDF）。圖 1（f）即為圖1（a）濁音語音幀的 LSAMDF。由圖 1（f）看出，LSAMDF與 EMDAMDF（圖1（e））相同，均能準確檢測出該濁音語音幀的基音。由此本文給出基于最小二乘法的AMDF基音檢測改進算法。

圖2 基于去均值下降趨勢的AMDF改進框架Fig.2 Framework for improving AMDF based on eliminating the falling trend

2 基于最小二乘法的AMDF改進算法

記一幀濁音語音信號的AMDF為γ，其中時延τ＝t1，t2，…，tn（式（1）），令 AMDF對應各時延 τ值為D（τ）＝γ1，γ2，…，γn。記 AMDF中所有樣本點為（t1，γ1），（t2，γ2），…，（tn，γn）。以線性多項式表示 AMDF均值下降趨勢為

最小二乘法估計參數α及β原理為最小化代價函數

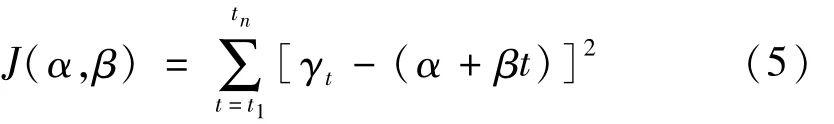
求解式（5）方法有多種，此處僅給出線性代數解法。定理［14］為：若A為秩n的m×n矩陣，則正規方程組 ATAx＝ATb有唯一解 x＾＝（ATA）－1ATb且 x＾為方程組Ax＝b唯一最小二乘解。將樣本點（t1，γ1），（t2，γ2），…，（tn，γn）代入式（4）得

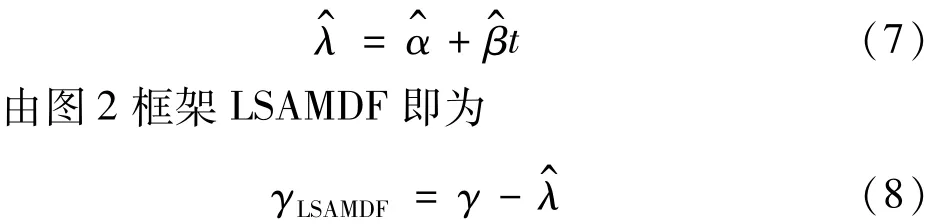
綜合以上分析，基于最小二乘法的AMDF基音檢測改進算法具體步驟為：① 計算待檢測語音幀的AMDF：γ；② 利用最小二乘法計算AMDF的均值下降趨勢＝＾＋＾t；③ 計算 LSAMDF：γLSAMDF＝γ－λ＾。

EMD與最小二乘法提取的AMDF（圖1（b））的均值下降趨勢（分別記為 EMDtrend及 LStrend）見圖3。由圖3看出，兩種下降趨勢基本相同，均能較好表示AMDF樣本點的基本動向；但圖3（c）EMD－trend與LS－trend在矩形框內部分差異較大，EMD－trend前端呈局部輕微上升趨勢；而EMD可精確捕捉時間序列下降趨勢的局部細節變化；但在圖2改進框架中提取均值下降趨勢無需十分精確。由于AMDF基音谷值候選點受其前端局部趨勢影響不大；而EMD提取均值下降趨勢需多次三次樣條擬合及去包絡均值計算，計算量明顯大于最小二乘法擬合線性趨勢。故認為LSAMDF綜合性能優于EMDAMDF。

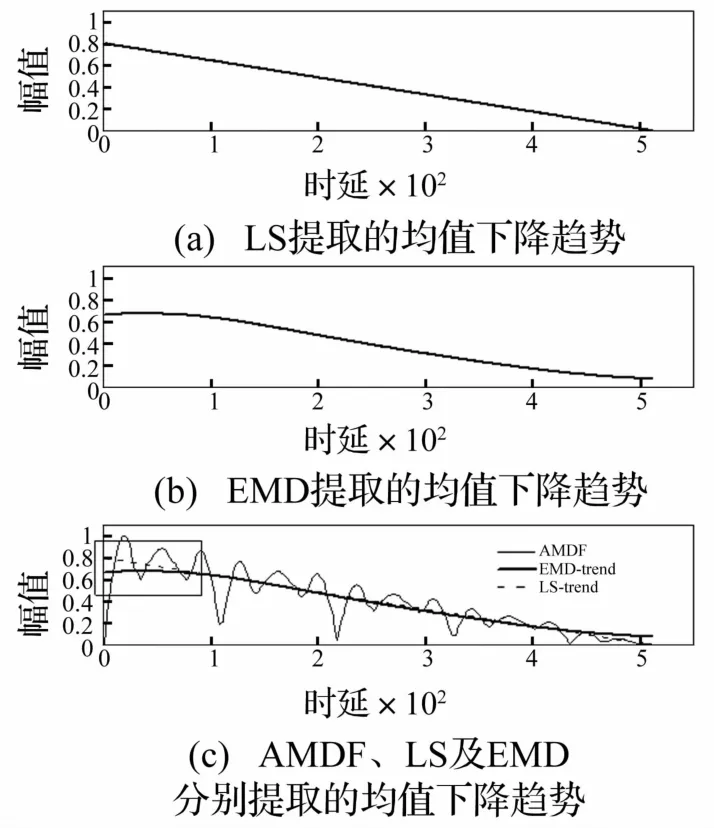
圖3 LS與EMD提取的均值下降趨勢Fig.3 Two falling trends extracted by LSand EMD respectively

3 仿真實驗與分析

實驗用基爾基音檢測參考數據庫（the Keele Pitch Extraction Reference Database）［15］對各種算法的基音檢測性能進行評價。該數據庫中所有語音均以20 000 Hz采樣，16 bits量化，并提供以512個采樣點為幀長、200個采樣點為幀移的所有濁音幀參考基音信息。實驗用AMDF、CAMDF、EAMDF、EMDAMDF及 LSAMDF檢測出基爾數據庫中編號為M1的男性語音信號前50幀基音軌跡，見圖 4。由圖 4看出，LSAMDF與 CAMDF、EAMDF、EMDAMDF均能較好克服AMDF的不足，檢測性能明顯優于AMDF；LSAMDF與EMDAMDF能避免CAMDF與EAMDF的部分錯誤（如第15、40幀）。

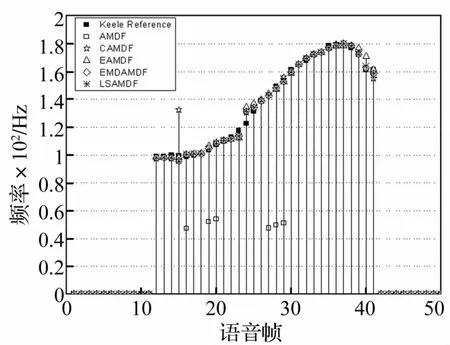
圖4 五種算法分別檢測的語音信號基音軌跡Fig.4 Pitch contrails of a speech signal detected by five algorithms respectively

為進一步驗證本文所提基于去均值下降趨勢的AMDF算法改進框架及以線性多項式表示均值下降趨勢假設的正確性及合理性，實驗仍用AMDF、CAMDF、EAMDF、EMDAMDF及 LSAMDF五種算法對 Keele數據庫中 5個樣本（編號 F1，F2，F3，M2，M3）進行基音檢測。檢測結果與數據庫中參考基音相對誤差大于或等于1 ms（以基音周期計算）定義為基音粗差（Gross Pitch Error，GPE）［16］，以%GPE作為指標比較各算法。需指出的是，由于基音頻率一般為50～500 Hz，實驗中所有待檢測樣本均進行50～500 Hz的帶通濾波。此外無任何預處理（如半波整流、中心削波等）及后處理（基音平滑等）步驟。

各種算法對5個樣本進行檢測的%GPE見表1。由表 1看出，CAMDF、EAMDF、EMDAMDF及 LSAMDF的%GPE均明顯低于傳統AMDF，說明均值下降趨勢對AMDF的性能影響較大，三類改進算法均能較好克服均值下降趨勢對AMDF影響；EMDAMDF及LSAMDF的%GPE基本無差距，均低于CAMDF及EAMDF，說明本文所提改進框架（圖2）的正確性。該框架與兩類改進AMDF方法（修正定義如CAMDF及補幀長如EAMDF）不但具有較大優勢，且以線性多項式近似表示均值下降趨勢完全合理可行。

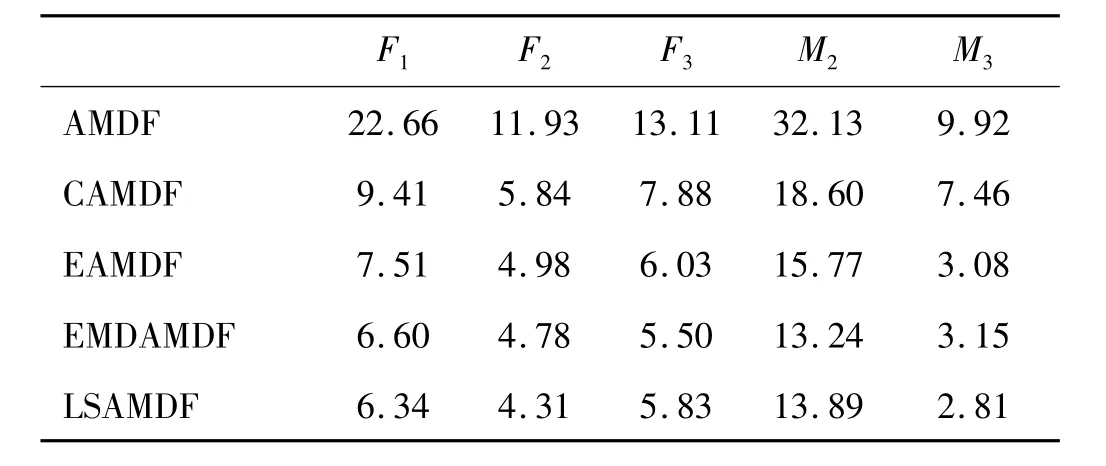
表1 五種算法檢測結果（單位：%GPE）Tab.1 Detection results of the five algorithms in terms of%GPE

最后，實驗中隨機選取每組100幀共三組濁音語音信號分別用五種算法進行檢測，統計執行時間。實驗用 PC機為聯想啟天 M4300（CPU：i3－2120（3.30 GHz雙核），內存：2G），軟件平臺為 MATLAB2009a。由表2看出，四種改進算法的平均執行時間分別為傳統AMDF的4.78、1.48、23.29、1.23倍，LSAMDF不僅擁有EMDAMDF的高檢測準確率，且算法復雜度明顯低于 EMDAMDF、CAMDF及EAMDF。結合圖4、表1、表2三組實驗看出，LSAMDF的綜合性能明顯優于其它三種改進算法。由此表明本文算法改進框架正確；以線性趨勢表示均值下降趨勢的假設合理可行。

表2 五種算法執行時間（單位：s）Tab.2 Performing time of the five algorithms in terms of Seconds

4 結 論

（1）本文提出基于去均值下降趨勢的AMDF基音檢測算法改進框架；通過分析AMDF的EMD分解提出利用線性趨勢表示AMDF的均值下降趨勢假設；利用最小二乘法擬合線性趨勢，從AMDF中減去近似下降趨勢，獲得改進的LSAMDF。

（2）仿真實驗結果驗證了去均值下降趨勢改進AMDF框架的合理性及以線性趨勢表示均值下降趨勢假設的可行性。LSAMDF性能明顯優于傳統AMDF、EAMDF及CAMDF且不劣于EMDAMDF，算法復雜度明顯低于EMDAMDF。

［1］Krubsack D A，Niederjohn R J.An autocerrelation pitch detector and voicing decision with confidence measures developed for noise corrupted speech［J］.IEEE Transactions on Signal Processing，1991，39（2）：319－329.

［2］Ross M，Shaffer H，Freudberg R，et al.Average magnitude difference function pitch extractor［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1974，22（5）：353－362.

［3］Ahmadi S，Spanias A S.Cepsrumbased pitch detection using a new statistical V／UV classification algorithm［J］.IEEE Transactions on Speech and Audio Processing，1999，7（3）：333－338.

［4］Kadame S，BroudreauxBartels G F.Application of the wavelet transform for pitch detection of speech signals［J］.IEEE Transactions on Information Theory，1992，38（2）：917－924.

［5］Shimamura T，Kobayashi H.Weighted autocorrelation for pitch extraction of noisy speech［J］.IEEE Transactions on Speech and Audio Processing，2001，9（7）：727－730.

［6］Amado G.Pitch detection algorithms based on zerocross rate and autocorrelation function for musical notes［C］.／／Proceedings of ICALIP.Shanghai：IEEE，2008：449－454.

［7］Zhang W，Xu G，Wang Y.Pitch estimation based on circular AMDF［C］.／／Proceedings of ICASSP. Beijing： IEEE，2002：341－344.

［8］Muhammad G.Noise robust pitch detection based on extended AMDF［C］.／／Proceedings of ISSPIT.Sarajevo：IEEE，2008：133－138.

［9］顧良，劉潤生.高性能漢語語音基音周期估計［J］.電子學報，1999，27（1）：8－11.GU Liang，LIU Runsheng.Highperformance mandarin pitch estimation［J］.Acta Electronica Sinica，1999，27（1）：8－11.

［10］梁升，王新晴，王東，等.基于 MMEMD的改進 HHT及應用［J］.振動與沖擊，2012，31（20）：23－26.LIANG Sheng， WANG Xinqing， WANG Dong， et al.Improved HHT based on MMEMD and its application［J］.Journal of Vibration and Shock，2012，31（20）：23－26.

［11］宗源，曾毓敏，孫永熙，等.基于EMD的AMDF基音檢測改進算法［J］.南京師范大學學報（工程技術版），2013，13（1）：62－67.ZONG Yuan， ZENG Yumin， SUN Yongxi， et al. A modified AMDF Pitch detection algorithm based on EMD［J］.Journal of Nanjing Normal University（Engineering and Technology Edition），2013，13（1）：62－67.

［12］李秀坤，李婷婷，馬濤.微弱信號強干擾分離方法研究［J］.振動與沖擊，2011，30（3）：225－227.LI Xiukun，LI Tingting，MA Tao.The research on strong interference separation of week signal［J］. Journal of Vibration and Shock，2011，30（3）：225－227.

［13］胡燦陽，陳清軍.基于EMD和最小二乘法的基線飄移研究［J］.振動與沖擊，2010，29（3）：162－167.HU Canyang，CHEN Qingjun.Research on baseline drift using leastsquare and EMD［J］.Journal of Vibration and Shock，2010，29（3）：162－167.

［14］Leon SJ.Linear algebra with applications［M］.New York：Macmillan，1980.

［15］ Meyer G，Plante F，Ainsworth W A.A pitch extraction reference database［C］.／／Proceedings of Eurospeech，Madrid：ISCA，1995：827－840.

［16］Rabiner L R，Cheng M J，McGonegal C A.A comparative performance study of several pitch detection algorithms［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1976，24（5）：399－417.