基于CFD氣動力辨識模型的氣動彈性數值計算

聶雪媛，劉中玉，楊國偉

（中國科學院 力學研究所 流固耦合系統力學重點實驗室，北京 100190）

對飛行器氣動彈性不穩定性預測在設計中非常重要。隨計算流體力學（Computational Fluid Dynamics，CFD）、計算結構力學（Computational Structure Dynamics，CSD）及計算機性能的發展，直接耦合CFD／CSD的數值模擬方法成為非線性氣動彈性分析中可信度最高方法［1］。然而在氣動彈性研究中，非定常氣動力計算占據大部分計算時間，使基于CFD的氣動彈性模擬難以在實際工程應用。如何既能保證計算精度又能提高計算效率成為氣動彈性的研究熱點。非定常流場模型降階技術 （ReducedOrder Models，ROMs）的出現為CFD／CSD數值模擬方法用于工程設計成為可能。降階模型由全流場全階CFD模型近似投影獲得低階模型，該模型能捕捉非線性流場動力學特征，計算效率遠高于CFD。非定常氣動力ROMs代替CFD與結構模型耦合，能進行氣動彈性分析或氣動伺服彈性分析及設計［2－3］。氣動力降階模型基于動態線性假設［4］，在給定非線性定常流場基礎上利用小擾動理論推導獲得到線性模型。在基于系統辨識的CFD降階模型方法中，Silva等［5］提出基于脈沖響應的Volterra級數模型降階方法，并與CFL3D結合進行氣動彈性顫振分析。但此方法需獲得系統全部Markov參數，而所用辨識數據因通過“一次激勵結構一個模態”獲得，會造成結構模態個數較多時所需脈沖響應個數呈冪函數增長。為此，文獻［6－7］開發出同時激勵結構多個模態方法提高辨識效率。認為輸入多個激勵信號間須存在相位差；但未給出如何確定相位差，需多次調試。Gupta等［8－10］提出采用飛行試驗中易實現的速度為3211信號作為輸入進行系統辨識。利用自回歸滑動平均模型（Autoregressive Moving Average，ARMA）作為替代CFD的降階模型。該方法亦需對各模態同時輸入的3211信號進行反復試驗、調整頻率，以期輸出響應能含希望激發的頻帶。為進一步提高效率，Raveh［11］用多個白噪聲信號模擬結構多模態同步輸入，辨識三種多輸入、輸出（Multiple Input Multiple Output，MIMO）模型，即頻域模型、ARMA模型及狀態空間模型，分析AGARD445.6機翼在跨聲速區域的顫振邊界。該方法雖可避免對輸入信號頻譜范圍要求，但仍未涉及多個輸入同步信號間相位差的確定。徐敏等［12－13］以一次激勵一個模態方式的階躍響應信號為輸入，基于Volterra級數方法建立非定常氣動力降階模型，并用于二維機翼氣動彈性主動控制及氣動彈性分析。張偉偉等［14］用3211信號建立基于CFD的 ARMA模型用于 Isogai機翼及AGARD445.6機翼氣動彈性分析，并認為輸入信號需反復調試。劉曉燕等［15］采用基于觀測器的Volterra核辨識方法，通過每個模態單獨激勵氣動力系統方式，在每個模態輸入含結構感興趣頻率正弦信號建立氣動力降階模型用于氣動彈性非線性氣動力預測及顫振抑制。該方法本質仍屬基于Volterra級數的ROMs。

為方便輸入信號選擇、避免同步輸入多信號時反復測試方可確定相位差、提高辨識計算效率，本文以隨機白噪聲信號為系統輸入，用一次激勵一個模態方式同時運行多個CFD數值模擬程序計算系統響應。利用所得多組訓練數據辨識出多個基于ARMA的單輸入多輸出（Single Input Multiple Output，SIMO）部分氣動力降階模型。因非定常氣動力建模建立于動態線性假設理論基礎上，故利用線性系統疊加原理獲得基于CFD的多輸入、輸出非定常氣動力降階模型，并將其與結構模型耦合用于AGARD445.6機翼顫振邊界預測。通過將預測結果與風洞試驗結果比較表明，本文所提建模方法準確、有效。

1 基于ARMA的氣動力降階模型

顫振邊界預測為氣動彈性分析中的重要計算及研究彈性體在小擾動激勵下系統響應，符合動態線性模型分類［16］，因此可用線性模型描述非定常氣動力，進行氣動彈性顫振分析。

本文所用氣動力降階模型進行氣動彈性顫振邊界分析過程可描述為將給定的結構模態位移一次一個模態輸入到非定常流場求解器，利用N－S方程求出各階模態對應的廣義氣動力，設關心結構的前n個模態，則會獲得n組“單輸入－n輸出”（記為1－n）的模型訓練數據，用系統辨識技術可得n個“1－n”的線性模型，利用線性系統疊加原理，最終獲得“n個輸入－n個輸出”（記為n－n）的氣動力降階模型，見圖1下方虛線框。用所得降階模型替代CFD與結構模型耦合，在結構振幅小擾動下通過改變動壓，可快速獲得結構位移響應，從而迅速找到某馬赫數下的顫振臨界參數，見圖1上方虛線框。此過程所耗時間與CFD／CSD耦合計算相比可忽略。

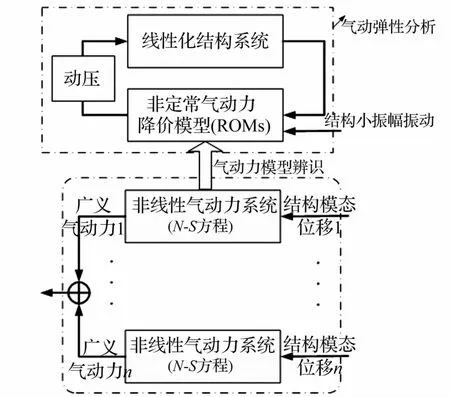
圖1 基于氣動力辨識模型的氣動彈性分析Fig.1 Aeroelastic analysis based on aerodynamic force identification model

本文所用氣動力降階模型為自回歸滑動平均ARMA模型，即時間域離散差分方程，形式為

式中：ya為n個廣義氣動力輸出組成的列向量；u為單模態位移輸入信號標量；na，nb為輸出、輸入延遲階數；k為離散時間變量；A，B為欲辨識系統模型參數。

設結構模態數為n（以下n均為結構前n階模態），則式（1）所描述的為圖1下方虛線框中每個“單模態位移輸入－n個模態廣義氣動力輸出”的1－n ARMA模型。據文獻［14］取4～8階延遲模型即可精確描述非定常效應，因此利用MATLAB的arx函數可較快辨識最好的表征訓練數據（式（1））最優的1－n ARMA模型。獲得1－n ARMA模型后用文獻［17］方法在Matlab中編程實現將離散差分方程轉換為離散狀態空間方程形式。第i階模態激勵下狀態空間方程為

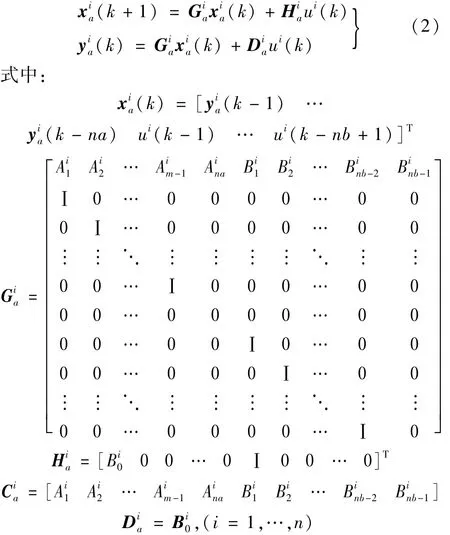
上述系數矩陣均為分塊矩陣。式（2）為第i階模態激勵下所得“單輸入－n輸出”的SIMO系統狀態空間方程。為便于氣動彈性分析，需獲得“n個模態輸入激勵下n個模態廣義氣動力輸出”的多輸入多輸出MIMO系統狀態空間模型。因此對n個 “單輸入－n輸出”狀態空間方程線性疊加，獲得所需MIMO狀態空間方程為

各參數中上標為模態階次。

2 激勵信號

模型辨識主要為激勵信號選取，要求所用激勵信號能激起被辨識系統所有頻段信號。隨機信號為含頻帶范圍最寬的信號，理論上用其作為激勵信號能獲得系統所有頻段范圍內響應。為實際氣動彈性工程應用，僅研究某特定頻率附近模態運動所致氣動力，對隨機信號進行帶通濾波處理。本文主要研究AGARD445.6機翼前四階模態 9.60 Hz、38.16 Hz、48.35 Hz、91.54 Hz引起的廣義氣動力。對輸入信號進行濾波，保證激勵信號包含該頻段即可。

輸入信號類型確定后，數據采樣頻率及長度將決定辨識精度。由于該激勵信號用于CFD計算，故其采樣時間與CFD計算時間步相同，本文為無量綱時間0.05，對應有量綱頻率 fs為 11 523.6 Hz（馬赫數為0.96時），其 Nyquist頻率為5 761 Hz，遠高于所需最高頻率91.54 Hz。對白噪聲激勵信號采用帶通方式濾波，保留頻段范圍為0.000 1fs～0.1fs。采樣長度據頻率分辨率定義需在CFD上運行約2 500個時間步，即可辨識系統最低頻率9.60 Hz。因此可獲得精度較高模型。雖運行2 500個時間步需耗費一定計算時間，但與頻繁修改參數進行CFD計算及氣動彈性分析的傳統方法相比，計算效率改善仍相當可觀。

圖2 機翼近壁面網格圖Fig.2 Mesh grid of near the wing

3 算例與分析

為驗證該辨識方法的有效性及準確性，本文對AGARD445.6進行模型辨識，利用辨識所得模型進行顫振邊界、顫振速度預測，并與風洞試驗結果比較。計算網格單元數約40萬。近壁面網格見圖2。CFD網格計算中首層網格厚度約為根弦長的8×10－5，結構振型歸一化見文獻［18］。采用非定常 N－S方程計算機翼彈性運動時非定常流場，空間采用基于結構網格技術的有限體積法，選HLLE格式進行空間離散，用代數無限插值法實現網格運動。用雙時間步進行時間離散，擬時間步為隱式格式LUSGS方法。施加模態位移激勵時需保證產生的結構實際位移、速度滿足線性擾動假設。

本文采用高斯白噪聲信號，在輸入CFD前先進行濾波處理。所選帶通范圍 0.000 1fs～0.1fs，其中 fs為CFD計算用采樣頻率。對應有量綱帶通約1.152～1 152 Hz。理論上為辨識出最低頻率，需至少2 500個時間步的CFD計算結果作為模型訓練數據，但實際應用中的ARMA模型，用200個時間步足夠，多余數據可用于校驗辨識的模型。由于針對結構前四階模態，因此只要辨識四個“單輸入－4輸出”的ARMA模型。模型辨識結果階次na＝4，nb＝5。

圖3為馬赫數0.96、輸入第一階模態位移為過濾高斯白噪聲信號時辨識模型與CFD計算所得氣動力見圖3，其中虛線為模型計算結果，實線為CFD計算結果。兩種方法計算結果吻合。

圖4為馬赫數0.96、給定第二階模態位移50 Hz正弦信號時辨識所得ARMA模型計算的氣動力與CFD直接計算的氣動力結果比較見圖4，其中虛線為模型計算結果，實線為CFD計算結果，可見二者吻合較好。

圖3 第一階模態激勵下辨識模型與CFD計算結果對比Fig.3 Comparison of ARMA model simulated responses and CFD response to excitation of the 1st mode

圖4 第二階模態激勵下辨識模型與CFD計算結果比較Fig.4 Comparison of ARMA model simulated response and CFD response to sinusoidal excitation of the 2nd mode

圖5 輸入3211信號Fig.5 3211 Excitation of the first four modes

三、四階模態激勵的模型準確性檢驗與一、二階類似。在檢驗辨識出的四個“單輸入－4輸出”ARMA模型準確性基礎上對其分別進行狀態空間轉換獲得（式（2））方程再進行線性疊加，最終獲得“4輸入－4輸出”氣動力狀態空間模型。對該空間模型精確度采用3211信號進行檢驗。輸入具有一定相位差的4個3211信號見圖5。在圖5信號輸入下“4輸入－4輸出”狀態空間模型計算的廣義氣動力與CFD直接計算結果比較見圖6，其中實線為CFD計算結果，方塊為“4輸入－4輸出”狀態空間模型計算結果。由圖6看出，MIMO系統狀態空間模型計算結果與CFD直接計算結果吻合較好為評價辨識模型計算精度，本文用常用評價模型準確度參數即模型擬合度為

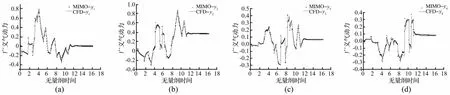
圖6 模型輸出與CFD計算結果比較Fig.6 Comparison of identification model simulated results and CFD results

式中：為CFD計算結果；為辨識模型計算結果；m為數據長度；η＝1為ARMA模型與N－S方程計算結果完全一致。

白噪聲信號、50 Hz正弦信號及3211信號作為結構模態位移輸入時，ARMA的模型擬合度見表1。由表1看出，所辨識模型精度較高。

表1 不同輸入信號激勵下模型擬合度Tab.1 Comparison of model fitness to different excitation signals

采用辨識模型預測的AGARD445.6機翼顫振頻率邊界及速度邊界見圖7、圖8。由二圖看出，耦合結構的N－S方程及ROM計算結果與風洞試驗結果均較吻合，且機翼顫振速度在跨聲速區域出現特有的“凹坑”現象。表明本文所用非定常氣動力模型辨識方法能用于跨聲速氣動彈性穩定性分析。

圖7 AGARD 445.6機翼無因次顫振頻率邊界Fig.7 Nondimensional flutter frequency boundary of AGARD 445.6 wing

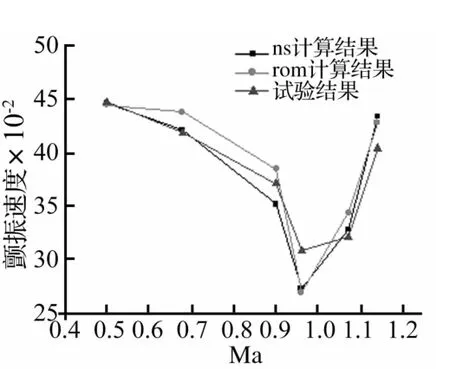
圖8 AGARD 445.6機翼無因次顫振速度邊界Fig.8 Nondimensional flutter speed boundary of AGARD 445.6 wing

基于系統辨識模型進行氣動彈性分析效率較高。如尋找馬赫數為0.96時的顫振臨界參數。采用求解非定常N－S方程方法搜尋一次參數至少需CFD運行2000個周期，若每個周期含20次內迭代（1次內迭代約3 s），運行時間約需2000 min（Intel Xeon 2.4 GHz雙CPU），而改變參數重新計算仍費時2 000 min。用非定常氣動力建模技術時以產生2 500個辨識用數據而言，需CFD運行2 500 min，而參數辨識時間在Matlab下約需10 s。故模型確定后搜尋一次參數，Matlab僅需1～2 s。

4 結 論

（1）本文以過濾隨機白噪聲信號為激勵信號，利用動態線性假設及線性系統疊加原理將辨識所得MISO系統ARMA模型線性疊加獲得MIMO系統模型，實現非定常氣動力建模。將辨識所得模型用白噪聲信號、正弦信號、3211信號等進行檢驗，并與直接CFD計算結果比較，從而驗證辨識模型的準確性。該方法與現有辨識方法相比，具有對激勵信號要求少、易于施加、辨識效率高等優點。

（2）將辨識所得時域信號變換為狀態空間模型用于AGARD445.6機翼顫振邊界預測。氣動力降階模型與結構模型耦合計算結果與CFD／CSD耦合計算結果及風洞試結果一致，表明本文方法不僅效率顯著提高，能用于氣動彈性穩定性分析，并為氣動伺服彈性分析及設計提供可能。

［1］陳剛，李躍明.非定常流場降階模型及其應用研究進展與展望［J］.力學進展，2011，41（6）：686－701.CHEN Gang，LI Yueming.Advances and prospects of the reduced order model for unsteady flow and its application［J］.Advances in Mechanics，2011，41（6）：686－701.

［2］Dowell E H.Eigenmode analysis in unsteady aerodynamics：Reducedorder models［J］.AIAA Journal，1996，34（8）：1578－1583.

［3］Lucia D J，Beran P S，Silva W A.Reducedorder modeling：new approaches for computational physics［J］.Progress in Aerospace Sciences，2004，40（1／2）：51－117.

［4］Dowell E H.A modern course in aeroelasticity，3rd Revised and Enlarged Edition［M］.New York：Klewer Academic Publishers，1995.

［5］Silva W A.Bartels R E.Development of reducedorder models for aeroelastic analysis and flutter prediction using the CFL3Dv6.0 code［J］.Journal of Fluids and Structures，2004，19：729－745.

［6］Silva W A. Simultaneous excitation of multipleinput multipleoutput CFDbased unsteady aerodynamic systems［J］.Journal of Aircraft，2008，45（4）：1267－1274.

［7］Kim T，Hong M，Bhatia K G，et al.Aeroelastic model reduction for affordable computational fluid dynamicsbased flutter analysis［J］.AIAA Journal，2005，43：2487－2495.

［8］Gupta K K，Voelker L S，Bach C，et al.CFDbased aeroelastic analysis of the X43 hypersonic flight vehicle［C］.Proceedings of the 39th Aerospace Sciences Meeting and Exhibit，2001.

［9］Cowan T J，Gupta K K.Accelerating CFDbased aeroelastic predictions using systems identification［C］.36th AIAA Atmoshperic Flight Mechanics Conference and Exhibit，1998：85－93.

［10］Cowan T J，Gupta K K. Development of discretetime aerodynamic model for CFDbased aeroelastic analysis［C］.Proceedings of the 37th Aerospace Sciences Meeting and Exhibit，1999.

［11］Raveh D E. Identification of computationalfluiddynamic based unsteady aerodynamic models for aeroelastic analysis［J］.Journal of Aircraft，2004（41）：620－632.

［12］徐敏，陳剛，陳士櫓.基于非定常氣動力低階模型的氣動彈性主動控制律設計［J］.西北工業大學學報，2004，22（6）：748－752.XU Min，CHEN Gang，CHEN Shilu.Design method of active control law based on reducedorder model of unste ady aerodynamics for aeroelasticity［J］.Journal of Northwestern Polytechnical University，2004，22（6）：748－752.

［13］姚偉剛，徐敏.基于Volterra級數降階模型的氣動彈性分析［J］.宇航學報，2008，29（6）：1711－1716.YAO Weigang，XU Min.Aeroelastic numerical analysis via Volterra series approach［J］.Journal of Astronautics，2008，29（6）：1711－1716.

［14］張偉偉，葉正寅.基于非定常氣動力辨識技術的氣動彈性數值模擬［J］.航空學報，2006，27（4）：579－583.ZHANG Weiwei，YE Zhengyin.Numerical simulation of aeroelasiticity basing on identification technology of unsteady aerodynamic loads［J］.Journal of Astronautics，2006，27（4）：579－583.

［15］劉曉燕.基于非定常氣動力降階模型的氣動彈性研究［D］.北京：北京航空航天大學，2011：54－61.

［16］Dowell E H，Crawley E F.A modern course in aeroelasticity［M］.Kluwer Academic，1989.

［17］Cowan T J， Gupta K K. Development of discretetime aerodynamic model for CFDbased aeroelastic analysis［R］.AIAA，1999.

［18］Carson Y E.Agard standard aeroelastic configurations for dynamic responseiwing 445.6［C］.AGARD－R－756，1988.