基于連續型風速風向聯合概率分布的風致結構疲勞分析方法研究
林濤濤,陳 雋1,,李 想,張曉琴
(1.土木工程防災國家重點實驗室,上海 200092; 2.同濟大學,上海 200092)
風致結構疲勞是細長高聳鋼制結構如天線、電視塔、燈柱、桅桿等重要的設計問題。據統計,既有結構80%以上的破壞由疲勞產生[1]。結構風致疲勞分析方法主要有時域法、頻域法和時-頻域法。時域法通過結構動力分析首先獲得考察點處的應力響應時程,再由循環計數法(如雨流法)來確定損傷值,計算可靠但效率低。頻域法基于隨機振動理論直接獲得關鍵點應力響應的統計特性,常用的有等效窄帶法[2]和上下限法[3],計算效率較高。時-頻域法綜合了時域法的精確性和頻域法的高計算效率[4],先通過隨機振動理論得到關鍵點的應力響應功率譜,再用Monte Carlo方法模擬應力過程,最后由雨流計數法獲得損傷值。
已有研究表明,風向的分布對結構疲勞壽命的預測有重要影響,忽略風向會低估結構的疲勞壽命。目前一般采用風速風向分離的離散區格方式考慮風向的影響,即先將風向分為若干區間(如常用的16風向區間),區間內再按風速大小分為若干區格。區格內采用一般算法計算風致疲勞損傷值,并以區格內風速發生概率作為損傷權重系數,再將區格損傷值累加得到總的損傷值。這種處理方式雖然考慮了風向的影響,然而各區格之間的風速函數在交界處不連續,同時區格大小(數量)的劃分受風速資料多少的限制。這些都會影響計算結果的準確性。因而,如何在風致結構疲勞壽命計算中更合理準確地考慮風速風向的聯合作用是一個值得深入研究問題。
本文利用對風速風向聯合概率密度函數(Joint Probability Density Function of wind speed and wind direction,簡稱JPDF)的研究成果[5],并結合等效窄帶法,將區格離散型的疲勞損傷累加求和公式推廣為連續型積分公式,理論上使得風致疲勞壽命計算更為合理和精確。通過將該方法用于一個圓形鋼質天線模型的風致疲勞壽命計算,證明了方法的可行性。
1 基于連續型JPDF的風振疲勞頻域分析方法
本節通過將JPDF和等效窄帶法結合,推導新的風致疲勞壽命計算方法。
1.1 微分區間的損傷值
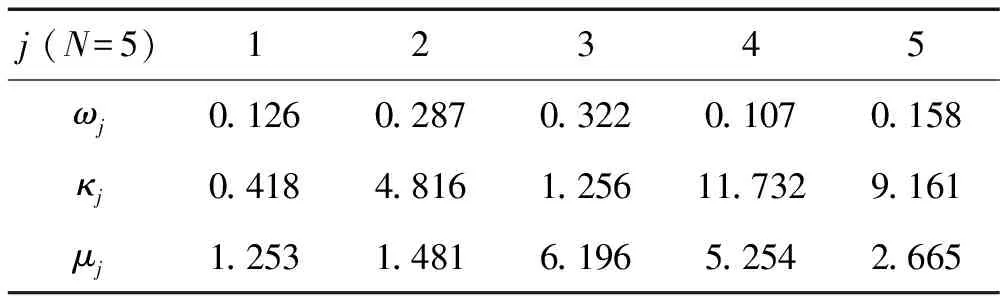
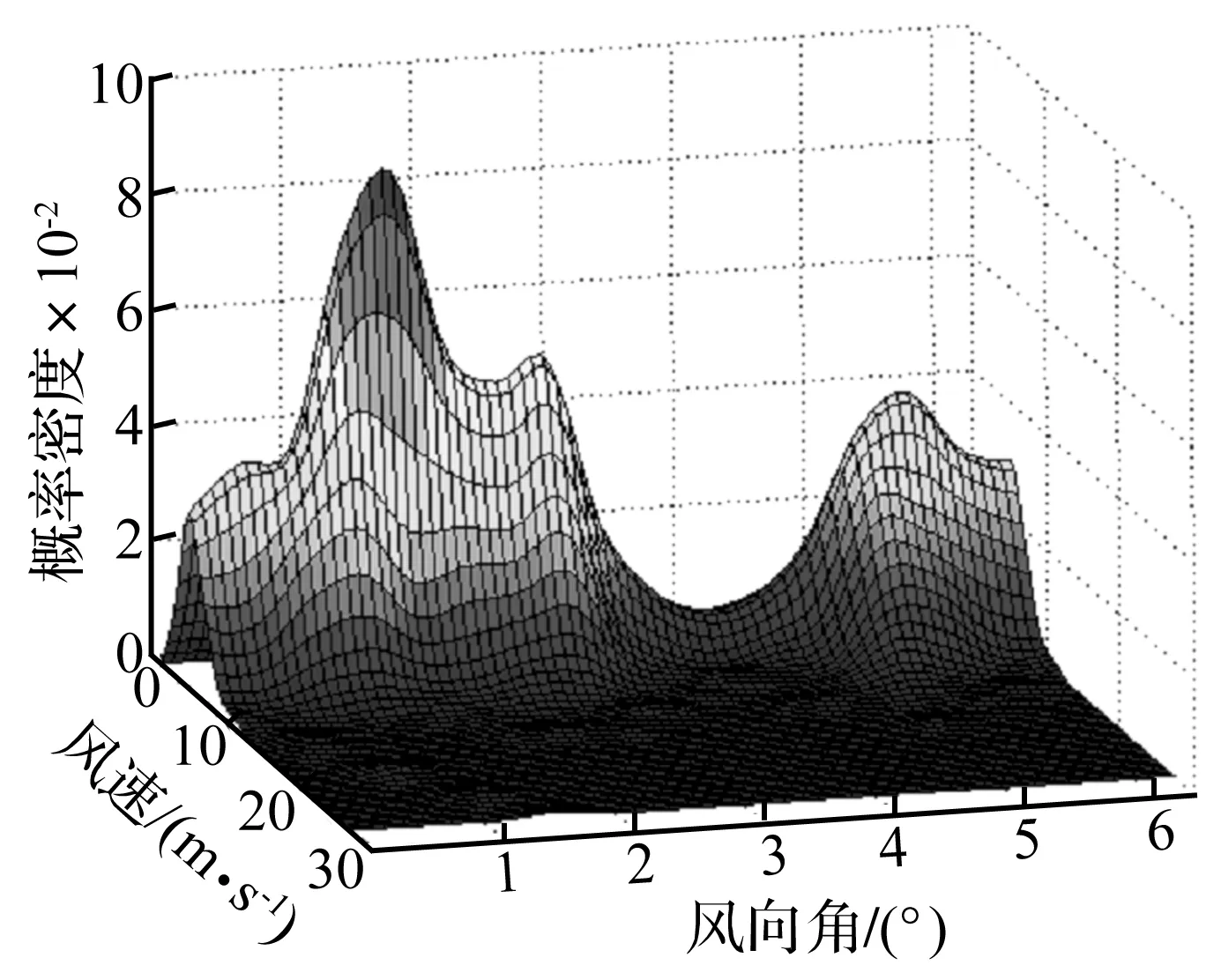
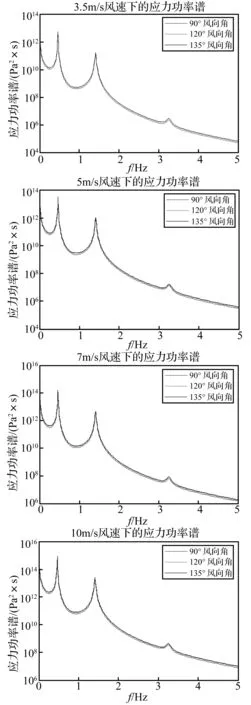
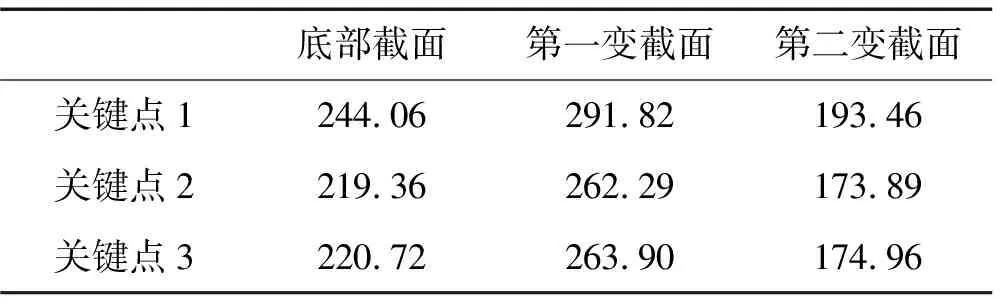
如前所述,目前一般在風速風向區間間隔(v 圖1 微分區間和區間間隔處理方式比較示意圖 根據等效窄帶法的假定,疲勞驗算點處的應力過程S(t)為零均值、窄帶平穩高斯過程,則微分區間(v (1) 式中,S是應力范圍;σSv,θ是相應于微分區間(v NSm=K (2) 式中,m、K是和材料有關的常數;N是相應于常應力范圍S時直到發生疲勞破壞的循環次數。 相應于微分區間(v (3) (4) 式中,α0v,θ、α2v,θ分別是相應于微分區間(v 由式(3)和式(4),可得到相應于風速風向的聯合微分區間(v (5) 則當應力范圍區間為(0,+∞)時,窄帶過程的損傷值為: (6) 將式(1)代入式(6),則相應于微分區間(v (7) 式中,Γ(*)為Gamma函數。 對于寬帶高斯應力過程采用式(7)時需對損傷預測值進行修正。根據文獻[2],可由實際應力功率譜的譜矩確定一個經驗上的寬帶修正系數λv,θ,以此來修正窄帶過程而得到寬帶過程的損傷值: (8) 式中,λv,θ是相應于微分區間(v λv,θ=a+(1-a)(1-εv,θ)b (9) 式中,a,b是與材料有關的參數,其分別由式(10)和式(11)確定;εv,θ是相應微分區間(v a=0.926-0.033m (10) b=1.587m-2323 (11) (12) 結合風速風向JPDF,在風速風向微分區間(v Pv,θ=fV,Θ(v,θ)dvdθ (13) 式中,fV,Θ(v,θ)為風速風向聯合概率密度函數。 則在全風速風向區間(0 (14) 令D=1,由式(14)可得連續積分形式的疲勞壽命計算公式為: (15) 在文獻[7]給出了公式(1)-(15)的全部推導過程和細節。 以上推導時若采用風速風向區間間隔(v (16) 對于式(16),令D=1,可得求和累加形式的疲勞壽命計算公式為: (17) 比較式(14)和(16),式(15)和(17)可知,由于引入了JPDF函數,損傷計算的區格累加形式變成了整個風速風向空間上的連續積分形式,使得疲勞損傷和疲勞壽命的計算在理論上更加合理。雙重連續積分形式在數值計算中可以任意設置數值離散積分間隔,可以達到滿意的精度;而雙重累加形式和風速風向頻度統計有關,要想達到滿意的精度,又需要重新統計風速風向頻度資料。此外,區隔累加形式的風速上限值為實測統計資料中的最大風速,而JPDF可選用任何合理的形式,從而包括更大風速情況的影響。以上這些特點都可提高疲勞損傷計算的精度。 文獻[5]對現有的風速風向的聯合分布函數模型以及它們的適用性進行了詳細地討論。主要模型包括:經驗模型、區間模型、雙高斯模型、角-線性模型、Farilie-Gumbel-Morgensternmoxign (FGM)模型和Simple C-Type Distribution (SC模型)等。本文采用文獻[5]推薦的FGM模型。 直接引入風速隨機變量V和風向隨機變量Θ,根據文獻[9]的研究,FGM模型的通用表達式為: FV,Θ(v,θ)=FV(v)× FΘ(θ)[1+δ(1-FV(v))(1-FΘ(θ))] (18) 式中,v、θ是風速值和角度值;FV,Θ(v,θ)是風速風向聯合累積分布函數(JCDF);FV(v)是風速累積分布函數(CDF);FΘ(θ)是風向CDF;δ是表示風速、風向之間聯合作用大小的相關性系數,其值在-1≤δ≤1之間,|δ|越小說明風速、風向之間的相關性越小,反之則越大。 式(18)兩邊分別對v和θ求偏導數,經過化簡整理,得到風速風向聯合概率密度函數(JPDF)的表達式為: fΘ(θ){1+δ[1-2FV(v))(1-2FΘ(θ)]} (19) 式中,fV,Θ(v,θ)是風速風向JPDF;fV(v)是風速概率密度函數(PDF);fΘ(θ)是風向PDF。 上述計算中需要風速和風向的概率密度函數模型。其中風速PDF模型取為正態-威布爾分布(Normal-Weibull distribution,NW模型)為: φ1,φ2)+ -∞≤v≤∞ (20) (21) φ1,φ2)dv (22) 式中,ω0為Normal分布模型所占的權重;α、β分別為Weibull分布模型中的形狀參數和尺度參數;φ1、φ2是和隨機變量單位一致的參數。 風向PDF取混合von Mises模型[10]: 0≤θ≤2π (23) (24) I0(κj)= (25) 式中,fΘ(θ)是風向PDF;N是混合von Mises模型的組成個數,本文取N=5;ωj為第j個von Mises模型所占的權重,滿足式(24);κj和μj是兩個參數,分別滿足κj≥0、0≤μj<2π;I0(κj)是0階修正的第1類Bessel函數。 分析實例采用文獻[11]D類地區某超高層建筑上的鋼質天線結構,該超高層結構的頂部標高(即天線底部標高)為246 m,天線結構總高為87 m,結構分為三段,從下往上三段天線的長度分別為34 m、27 m、26 m,三段天線對應的截面外徑分別為2.4 m、1.75 m、1 m,三段天線對應的截面壁厚分別為3 cm、2.5 cm、2 cm(見圖2)。天線所用鋼材的質量密度為7.85×103kg/m3;結構阻尼采用Rayleigh阻尼,阻尼矩陣由質量矩陣和剛度矩陣決定,即[C]=a[M]+b[K],a,b為常數,對于鋼質天線結構,取前4階的阻尼比為0.01。結構動力特性分析采用集中質量法。在僅考慮順風向荷載作用下,圓形截面結構的風致疲勞壽命較低的關鍵點(即最危險關鍵點)往往出現在風向發生頻度較高的位置(關于圓心對稱的關鍵點的疲勞壽命也較低),則根據風速風向發生概率,所取關鍵點位置與X軸夾角分別為90°、120°、130°(見圖2)。順風向脈動風速譜采用Kaimal譜,順風向空間相關函數采用Shiotani模型。 天線結構的振動有X和Y兩個方向,且質量和剛度關于X和Y兩個方向都是對稱的,這大大簡化了整個分析和計算過程。在此規定,奇數階振型和頻率是X方向的,偶數階振型和頻率是Y方向的。前6階頻率見表1。 計算步驟:①整理風速風向實測數據;②使用Mathcad軟件擬合風速PDF和風向PDF模型參數,獲得模型表達式;③使用Matlab軟件擬合JPDF模型中的相關性系數,獲得JPDF表達式;④分析實例的動力特性;⑤選擇控制截面及控制點;⑥編程計算疲勞壽命。 圖2 鋼天線模型 表1 前6階頻率表 JPDF模型參數的計算數據為上海龍華氣象站1956年1月1日至1990年12月31日全部12784天10米高度處的日最大風速值(10分鐘平均時距)和相應的風向記錄的統計結果。為了避免不同樣本值之間的相關性,按照階段極值抽樣方法,抽取8天時間間隔的極值風速組成極值子樣[12]。 采用Mathcad軟件進行風速PDF和風向PDF各參數的擬合,采用Matlab軟件進行相關性系數δ的擬合。需要注意的是參數擬合屬于最優化問題,當擬合初值不同時,參數擬合結果會有所不同,但擬合優度R2接近。 風速PDF和風向PDF各參數的擬合結果分別見表2和表3。FGM模型中的相關性系數δ的擬合結果為0.0993125。擬合優度達到0.970350,可見FGM模型的精度是相當令人滿意的。圖3和圖4分別是實測的JPDF和擬合的JPDF,比較看出,擬合效果相當好。 表2 風速PDF模型參數擬合值 表3 風向PDF模型參數擬合值 圖3 實測的JPDF 圖4 擬合的JPDF 圖5 第二變截面關鍵點2處不同風速風向角下的應力功率譜 在數值計算時,風向角度間隔取為15°,10 m高度處的風速間隔取1 m/s;風速的上限值取10 m高度處對應的20 m/s,此上限值已經足夠滿足數值積分的精度要求;根據《鋼結構設計規范 GB 50017-2003》,假定構件類別為第8類,則參數K取值為4.1×1011,參數m取值為3。 根據風速風向JPDF的分布形式,考慮風向發生概率等綜合因素,所選取的疲勞分析關鍵點位置為天線結構最外邊緣,且與X軸方向夾角分別為90°、120°、130°。計算截面分別為底部截面、第一變截面、第二變截面,如圖2所示。 圖5給出了天線結構底部截面和第二變截面關鍵點2處在不同風速風向角下的應力功率譜圖,風速是10 m高度處的風速,從圖中可以看出隨著風速的增大,應力功率譜值是增大的;在結構對應的自振頻率處,其功率譜值達到峰值。 根據連續積分形式的疲勞壽命計算公式(15),計算得到底部截面、第一變截面和第二變截面各關鍵點的疲勞壽命,見表4。最終認為頻域計算方法估算的疲勞壽命為:173.89年。 表4 關鍵點疲勞壽命(單位:年) 本文結合連續型的風速風向聯合概率密度函數(JPDF),推導了基于等效窄帶法的連續積分形式的疲勞壽命計算公式,使得疲勞壽命的估算公式在理論上變得更加合理準確。應用于實例工程的疲勞壽命預測表明了連續積分形式計算公式的可行性。為更加精確的疲勞壽命估算提出了一條新思路。 [1] Repetto M P.Wind-induced response and fatigue of slender vertical structures [D].Universita Degli Studi Di Genova,2003. [2] Wirsching P H,Light M C.Fatigue under wide band random stress[J].Journal of Structural Division.1980,106(7): 1593-1607. [3] Holmes J D.Fatigue life under along-wind loading-closed-form solutions[J].Engineering Structures.2002,24(1): 109-114. [4] Gu M,Xu Y L,Chen L Z,et al.Fatigue life estimation of steel girder of Yangpu cable-stayed Bridge due to buffeting[J].Journal of Wind Engineering and Industrial Aerodynamics.1999,80: 383-400. [5] 張曉琴.風速風向聯合分布模型與應用研究[D].上海:同濟大學,2011. [6] 俞載道,曹國敖.隨機振動理論及其應用 [M].上海: 同濟大學出版社,1988. [7] 林濤濤.基于風速風向聯合概率密度函數的結構風致疲勞計算方法研究 [D].上海:同濟大學,2013. [8] 王欽華.復雜結構風致疲勞的理論和應用研究[D].上海:同濟大學,2009. [9] Erdem E,Shi J.Comparison of bivariate distribution construction approaches for analysing wind speed and direction data[J].Wind Energy,2011,14 (1): 27-41. [10] Carta J A,Bueno C,Ramirez P.Statistical modelling of directional wind speeds using mixtures of von Mises distributions: Case study[J].Energy Conversion and Management,2008 (49): 897-907. [11] 李想.基于風速風向聯合分布函數的結構風致疲勞壽命計算方法研究[D].上海:同濟大學,2011. [12] 楊詠昕,葛耀君,項海帆.風速風向聯合分布的平均風統計分析[J].結構工程師,2002 (3): 29-36. YANG Yong-xin,GE Yao-jun,XIANG Hai-fan.Statistic analysis of wind speed based on joint distribution of wind speed and wind direction [J].Structural Engineers,2002(3):29-36.

1.2 寬帶修正
1.3 全部風速風向區間內的累積損傷計算
1.4 與離散區格公式的區別及聯系

2 JPDF的選取
2.1 FGM模型
2.2 風速PDF模型和風向PDF模型
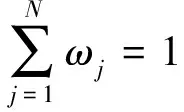
3 實例分析
3.1 實例概況




3.3 疲勞壽命估算
4 結 論

