高速列車系統動力學空氣彈簧建模方法研究

戚 壯，李 芾，黃運華，虞大聯

(1.西南交通大學 機械工程學院，成都 610031;2.南車青島四方股份 國家工程實驗室，山東 青島 266111)

作為二系懸掛裝置，空氣彈簧目前已廣泛應用于現代高速列車上。由于空氣彈簧是一個多物理變量的非線性系統，如何在高速列車動力學計算中建立空氣彈簧模型，已成為國內外學者研究的焦點。

Oda等［1］利用“彈性支撐阻尼”系統建立了適用于更寬頻域范圍的“Nishimura”模型，但是該模型并沒有考慮氣體在管路中的慣性效應。Krettek等［2］基于流體力學與氣動力學原理，簡化了空氣彈簧的計算公式，建立了空氣彈簧非線性氣動模型。Nieto等［3－5］基于空氣熱動力學原理，對橡膠氣囊、附加空氣室、節流孔和其間的連接管路分別進行建模，再將其用統一的微分方程組進行描述。這類模型考慮了空氣彈簧內部氣體的運動特性以及溫度、壓強的變化對空氣彈簧動態特性的影響，可稱為空氣彈簧的完全模型。

我國將空氣彈簧廣泛應用于軌道車輛只有20多年的時間［6］，但已有諸多學者對空氣彈簧的建模方法進行了卓有成效的研究。李芾等［7］基于熱力學及流體力學理論，推導了空氣彈簧物理模型的統一數學表達式。張廣世等［8］基于SIMULINK平臺，建立了帶有連接管路的空氣彈簧動力學模型。張利國等［9］對空氣彈簧的現狀及其發展作了綜述性總結。王家勝等［10］對空氣彈簧的動剛度進行了線性化研究。但是，在國內大部分高速列車動力學計算中，空氣彈簧仍采用線性模型［11］。

綜上所述，高速列車動力學計算中空氣彈簧的建模方法主要分為三類:線性模型、非線性模型和完全模型。這三類模型對動力學計算結果有何影響，正是以下研究的主要內容。

1 空氣彈簧動力學模型

1.1 線性模型

線性模型是將空氣彈簧的動剛度和動阻尼等效為一個鋼彈簧并聯一個阻尼器，如圖1所示，其中鋼彈簧的等效剛度Ke與阻尼器的等效阻尼Ce均為定值，由空氣彈簧的動剛度試驗確定。由于線性模型建模簡便、參數直觀、計算速度快，該模型目前廣泛應用于高速列車的動力學計算中。

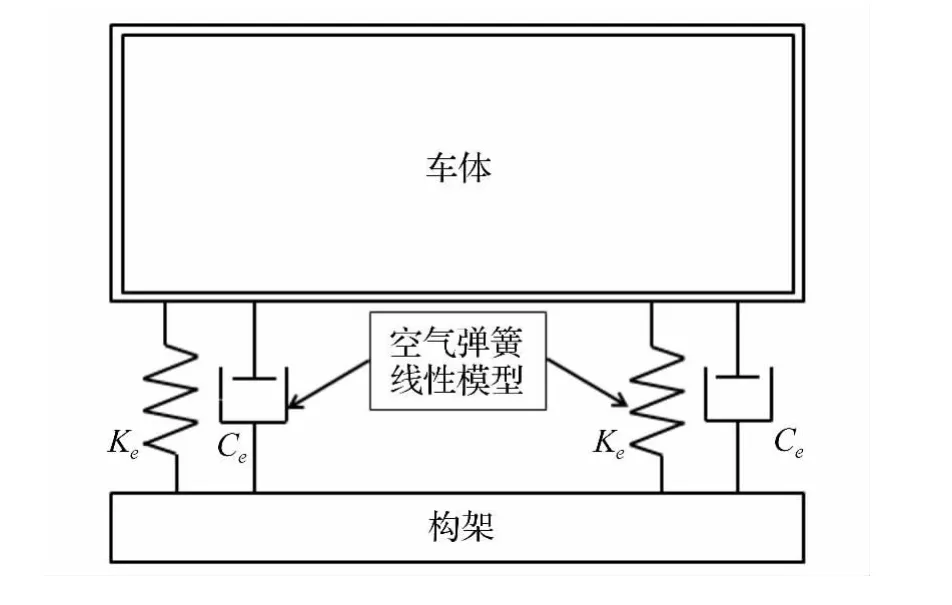
圖1 空氣彈簧線性模型Fig.1 The linear model of air spring

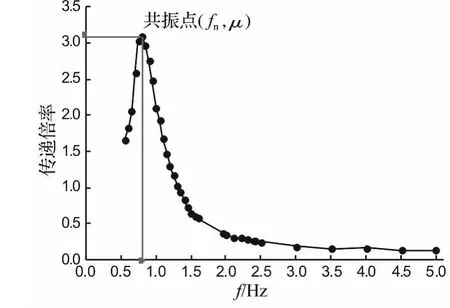
圖2 空氣彈簧振動特性曲線Fig.2 The vibration character curve of air spring

空氣彈簧線性模型中的等效剛度Ke與等效阻尼Ce需要對空氣彈簧進行動剛度試驗確定。根據相關標準［12］對空氣彈簧進行動剛度試驗。在空氣彈簧上面放置一個摩擦力極小并作垂直方向導向的秤錘，該秤錘的質量m要使空氣彈簧內壓力達到空氣彈簧正常使用時的要求。在空氣彈簧底部施加頻率為0.5－5 Hz，振幅為3 mm的簡諧振動，測量空氣彈簧上秤錘的垂向振幅，并以加振頻率為x軸，秤錘振幅與加振振幅的比(傳遞倍率)為y軸，得到某次試驗中空氣彈簧的振動特性曲線如圖2所示。

根據振動特性曲線，可以得到該空氣彈簧的共振點。共振點的橫坐標對應共振頻率fn，縱坐標對應共振倍率μ。則其等效剛度Ke和等效阻尼Ce分別由下式進行計算［12］:

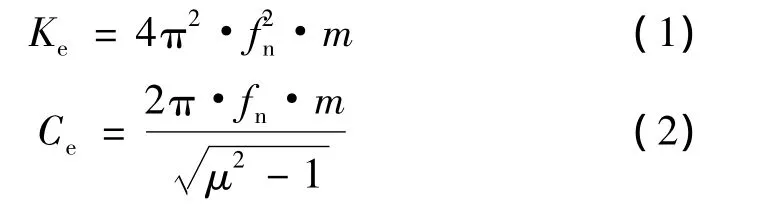
式中，π為圓周率常數。

1.2 非線性模型

基于流體力學和氣動力學原理，可以建立描述空氣彈簧內部氣體運動的微分方程組，從而建立空氣彈簧的非線性模型［2，7］。非線性模型將橡膠氣囊與附加空氣室中氣體的熱動力學變化過程視為等熵過程，滿足氣體的多變過程方程:

式中:i=b時，表示橡膠氣囊，i=t時，表示附加空氣室;0為表示某一物理量的初始狀態;pi為橡膠氣囊或附加空氣室內部壓強(Pa);Vi為橡膠氣囊或附加空氣室容積(m3);n為氣體的多變指數，在絕熱過程中取1.4。

將橡膠氣囊與附加空氣室內部的氣動力學方程進行聯立，并將微分方程線性化，可得到橡膠氣囊內部壓強的表達式為:

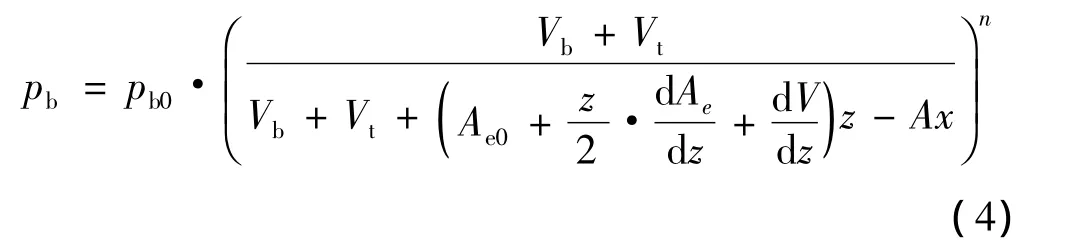
式中:Ae為空氣彈簧的有效面積(m2);A為橡膠氣囊與附加空氣室之間連接管路的截面積(m2);x為連接管路中氣體的位移(m);z為空氣彈簧上下表面的距離(m)。

橡膠氣囊與附加空氣室之間連接管路中的氣體視為恒定質量塊在管路中的運動，考慮氣體的慣性效應和氣體與管壁的摩擦損耗，基于流體力學公式，可得到管內氣體的運動方程為:

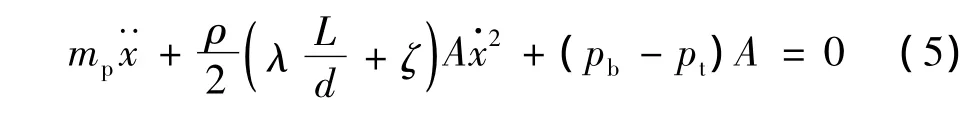
式中:mp為管內氣體的質量(kg);ρ為管內氣體的密度(kg/m3);λ為沿程阻力系數;ζ為局部阻力系數;L為連接管路長度(m);d為連接管路內徑(m)。

考慮到橡膠氣囊自身具有的阻尼作用，其對車體的支撐力以及對構架的反力F的表達式為:

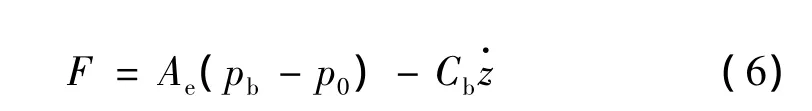
式中:p0為大氣壓強(Pa);Cb為橡膠氣囊自身阻尼(N·s/m)。

此外，對于應急橡膠堆，當空氣彈簧的上下表面沒有貼靠時，即z＞0時，由于其剛度遠大于空氣彈簧的剛度，可認為應急橡膠堆不起作用;當空氣彈簧的上下表面開始貼靠時，即z=0時，可將應急橡膠堆視為剛度Kr與阻尼 Cr并聯的線性力元。因此，聯立式(4)－(6)，即可建立如圖3所示的空氣彈簧的非線性模型。

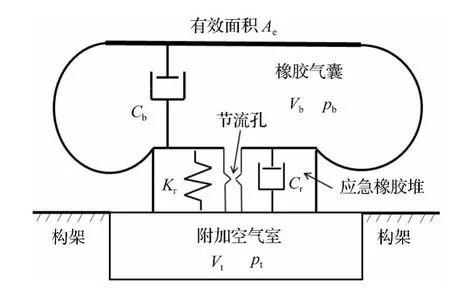
圖3 空氣彈簧非線性模型Fig.3 The non-linear model of air spring

1.3 完全模型

完全模型需要對空氣彈簧懸掛系統的各個部件分別進行建模［3－5］，其中包括橡膠氣囊、附加空氣室、節流孔、高度調整閥、差壓閥等。描述橡膠氣囊和附加空氣室的數學方程可參考(4)式。基于空氣動力學原理，重新建立的氣體流經節流孔的運動方程如下式:

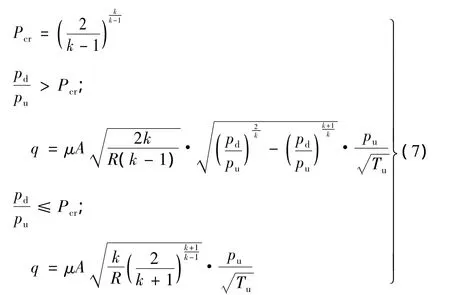
式中:Pcr為氣體的臨界壓力比，用來判斷氣體的流速是否大于聲速;pd，pu為分別為節流孔下游和上游的絕對壓強(Pa);Tu為節流孔上游溫度(K);μ為流量系數，一般μ＜1，由試驗確定;A為節流孔面積(m2);R為理想氣體常數，一般取287.1 J/(kg·K);k為氣體的比熱比，一般取1.4;q為氣體流經節流孔的流量(kg/s)。

當車體高度超出高度調整閥的無感區后，高度調整閥在一定的延遲時間后打開，對橡膠氣囊進行充氣或放氣，以調整車體高度。根據高度調整閥的動作特性，其數學模型可等效為一個二階系統的傳遞函數，如下式:

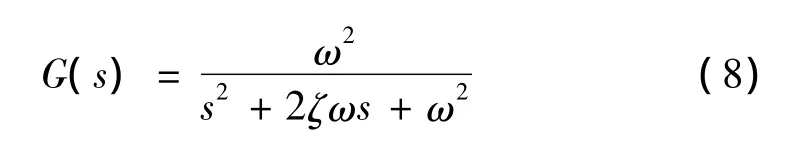
式中:G(s)為高度調整閥模型的傳遞函數;s為拉普拉斯變換后的變量;ω，、ζ為高度調整閥模型中的參數。

當兩側空氣彈簧壓強差超出預定范圍時，差壓閥打開，氣體從高壓側流向低壓側，以保證車輛的運行安全。差壓閥的數學方程可表示為:

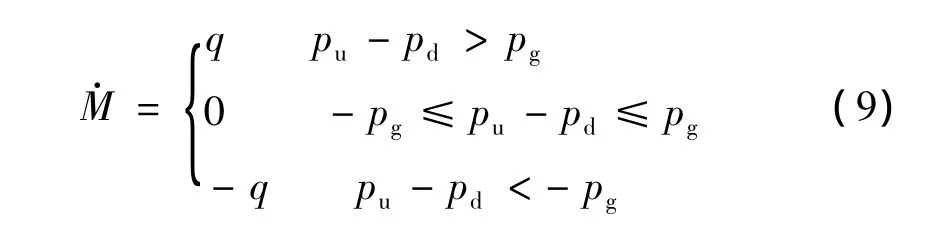
式中:pg為差壓閥預先設定的壓強差(Pa);pd，pu為分別為差壓閥下游和上游的絕對壓強(Pa);M·為氣體流經差壓閥的流量(kg/s)，可通過(7)式計算。

此外，完全模型還考慮了空氣彈簧內部氣體與外界的熱量交換，其交換熱量按照下式計算:

式中:i為表示空氣彈簧的不同部分，i=b時，表示橡膠氣囊;i=t時，表示附加空氣室;i=p時，表示連接管路;Qi為內部氣體與外界的熱交換功率(W);γi為不同位置的導熱系數(W/(m.K));Si為不同位置的熱交換面積(m2);Ti為不同位置的溫度(K);Ta為外界大氣溫度(K);εi為管壁、氣囊或附加氣室壁的法向厚度(m);

將式(7)～式(10)與式(4)和式(6)聯立，即可建立空氣彈簧的完全模型。由于完全模型涉及的物理量較多，可在AMESim平臺上構建，如圖4所示。

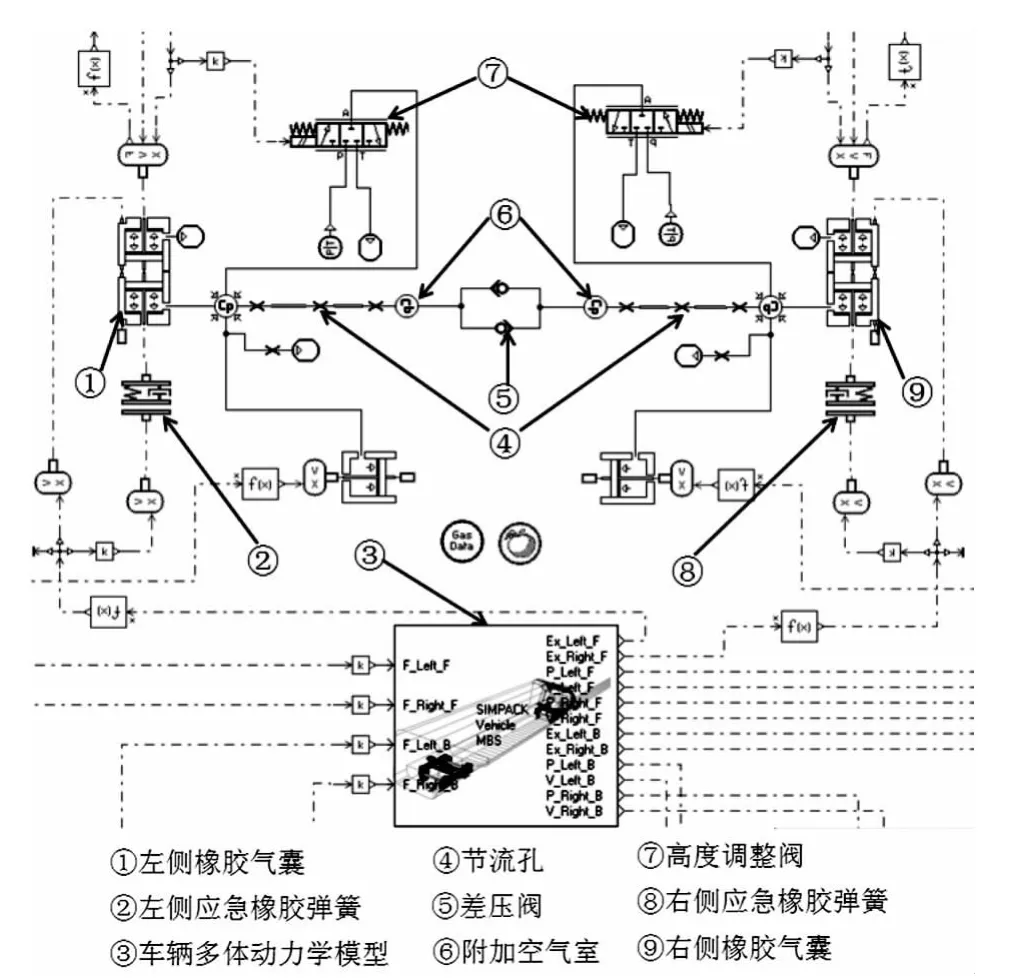
圖4 空氣彈簧完全模型Fig.4 The complete model of air spring

2 準靜態動力學特性

2.1 激振載荷的確定

為了便于對比，計算中均以某型動車組及其空氣彈簧為算例，該型車空氣彈簧主要結構參數與車輛主要動力學參數見表1。

表1 數值計算中的主要參數Tab.1 Main parameters of numerical calculation

為了確定在準靜態動力學特性分析中對空氣彈簧施加的激振載荷，首先以傳統方法對該型高速動車組進行動力學計算。在仿真中設定，軌道譜為京津高鐵實測軌道譜，車輛在40 s內以350 km/h的速度在平直線路上作勻速運動。在計算結果中，取出車體與構架之間在空氣彈簧處相對位移的時間歷程，如圖5(a)所示。該相對位移即可視為高速列車在運行的過程中對空氣彈簧的激勵。由激振的時間歷程可知，對空氣彈簧的激振幅值大部分集中于3 mm左右。對激振的時間歷程進行快速傅立葉變換，如圖5(b)所示，激振頻率主要集中在1 Hz左右。因此，在準靜態動力學特性分析中，選取振幅為3 mm，頻率為1 Hz的正弦波作為空氣彈簧的激振。

圖5 空氣彈簧激振的時間歷程及快速傅里葉變換Fig.5 The time history of excitation to the air spring and its Fourier transformation

2.2 準靜態動力學仿真

將空氣彈簧的上表面固定，并預加載車體對空氣彈簧的靜態壓力。對空氣彈簧的下部施加振幅為3 mm，頻率為1 Hz的正弦激勵，測量空氣彈簧上表面對車體支撐力的變化。三種模型的力—位移回滯曲線如圖6所示。

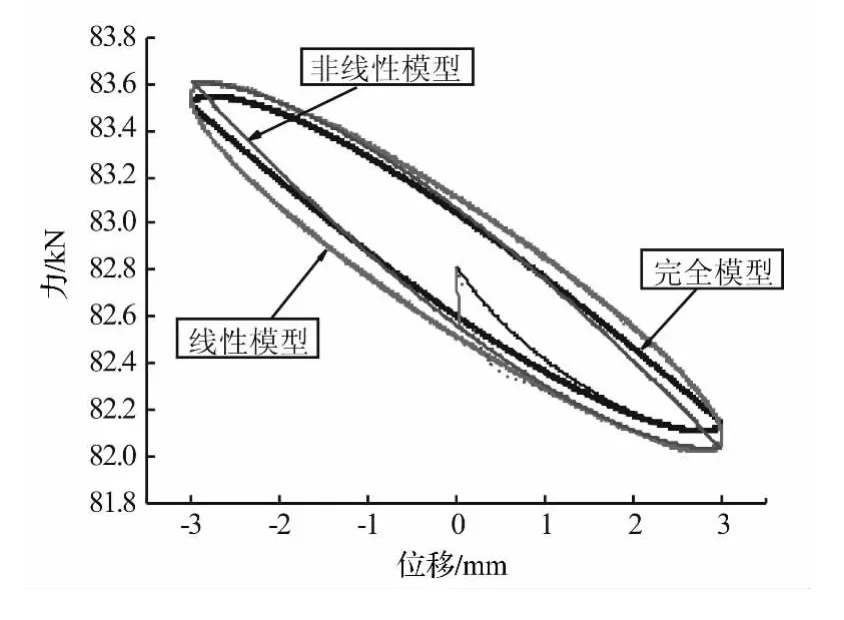
圖6 三種空氣彈簧動力學模型的回滯曲線Fig.6 The hysteresis curves of the three dynamic models of air spring

由該回滯曲線可以看出，線性模型的回滯曲線呈橢圓形，且包圍了更大的面積，說明線性模型具有較高的阻尼特性。非線性模型和完全模型回滯曲線的形狀較相似，與線性模型的橢圓形回滯曲線相比，前兩者模型回滯曲線的兩端較尖扁。這體現了空氣彈簧的非線性特性。因此，在準靜態仿真中已可以看出這三種空氣彈簧動力學模型動態特性的差異，但是這些差異究竟會對高速列車的動力學計算產生何種影響，還需要在整車動力學計算中進行探究。

3 整車動力學性能研究

將三種空氣彈簧動力學模型引入前述高速動車組的整車動力學模型中，根據《高速動車組整車試驗規范》［13］對其進行動力學計算，以研究在不同空氣彈簧動力學模型下高速動車組的動力學性能。

3.1 車輛運行安全性的計算

首先計算在三種空氣彈簧動力學模型下高速動車組通過曲線時的運行安全性。設定車輛通過的曲線半徑為7 000 m，緩和曲線的長度為670 m，曲線超高為150 mm，軌道不平順激勵為京津城際高鐵軌道譜。計算車輛以不同的速度通過該曲線時，輪軌垂向力、輪軸橫向力、脫軌系數、輪重減載率和傾覆系數最大值，如圖7所示。

由圖7的計算結果可以看出，三種模型計算出的車輛運行安全性指標基本一致。以完全模型為參照，非線性模型與線性模型相比于完全模型在各種速度級下的最大相對誤差如圖8所示。由相對誤差的對比可得到以下結論:相比于線性模型，非線性模型與完全模型的運行安全性計算結果更為接近;在幾項安全性指標中，輪重減載率與傾覆系數的相對誤差較大，這是因為車體的偏載導致空氣彈簧內部壓強的變化，從而引起空氣彈簧動態剛度的變化，而線性模型的剛度始終為定值;雖然線性模型相比于非線性模型計算誤差稍大，但其與完全模型的計算誤差仍在4%以內，這是由于二系懸掛特性的差異對輪軌作用力的影響相對較小。因此，用線性模型與非線性模型計算高速列車的運行安全性，可以滿足工程要求。

圖7 三種模型的車輛運行安全性指標Fig.7 The vehicle safety index of the three dynamic models of air spring

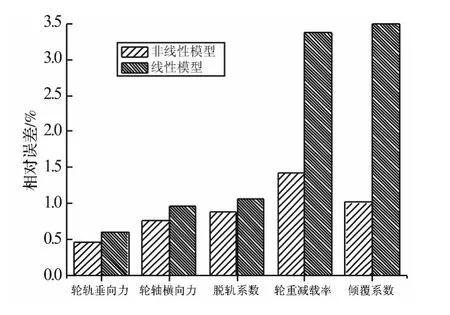
圖8 非線性模型、線性模型與完全模型相比的相對誤差Fig.8 The relative error of non-linear and linear models compared to complete model

3.2 車輛運行平穩性的計算

在直線工況下計算車輛的運行平穩性，軌道激勵仍采用京津城際高鐵軌道譜。平穩性計算結果主要包括車體橫向、垂向加速度的最大值以及車體的垂向、橫向平穩性。在車體前轉向架中心地板面上設置加速度計，在計算結果中輸出每步積分的加速度值。車體的平穩性按照下式計算:

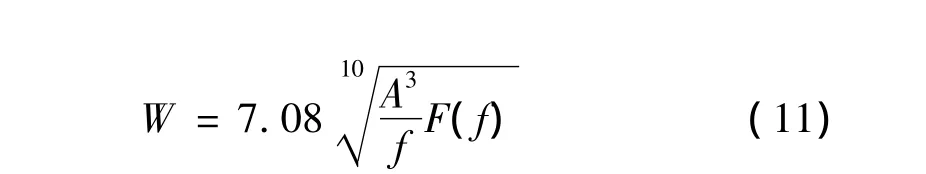
式中W、A、f和F(f)的具體定義詳見文獻［13］。平穩性指標越小，說明車體的振動越小，標準中規定的1級平穩性指標應小于2.5。在不同速度下計算出的車輛各項平穩性指標如圖9所示。

由車輛運行平穩性的計算結果可以得出以下結論:車體橫向加速度與橫向平穩性在三種模型下計算結果基本一致，這是由于三種模型均假設空氣彈簧的垂向剛度與水平剛度沒有耦合性;車體垂向加速度與垂向平穩性在三種模型下的計算結果誤差較大，這是由于三種模型動態特性的差異對車體垂向振動的影響較大;對于車體垂向加速度與垂向平穩性，完全模型與非線性模型在250－350 km/h速度級之間具有非線性特性，而線性模型的指標隨車速的變化基本呈線性變化。因此，在高速列車動力學中計算車體垂向平穩性，應用線性模型對空氣彈簧進行建模會與實際情況產生較大的差異。

將三種空氣彈簧動力學模型在整車模型下仿真的計算時間進行對比。整車仿真時間設定為40 s，積分步長設置為0.005 s，計算機CPU為2.93 GHz的雙核奔騰處理器，三種模型在某一工況下的仿真時間對比如表1所示。由三種模型的計算耗時對比可知，線性模型的計算速度最快，非線性模型稍慢，而完全模型的計算時間是前兩者的2.5倍左右。由此可知，在高速列車的動力學計算中，雖然完全模型的計算結果更為準確，但其計算速度較慢，且涉及的物理參量較多，不易確定;線性模型的計算速度較快，但不能體現空氣彈簧的非線性特性;而非線性模型的計算速度和線性模型基本相同，且計算結果較為準確。因此，在高速列車的動力學計算中建議采用非線性模型對空氣彈簧進行建模。

圖9 三種模型的車輛運行平穩性指標性Fig.9 The vehicle ride comfort index of three dynamic models of air spring

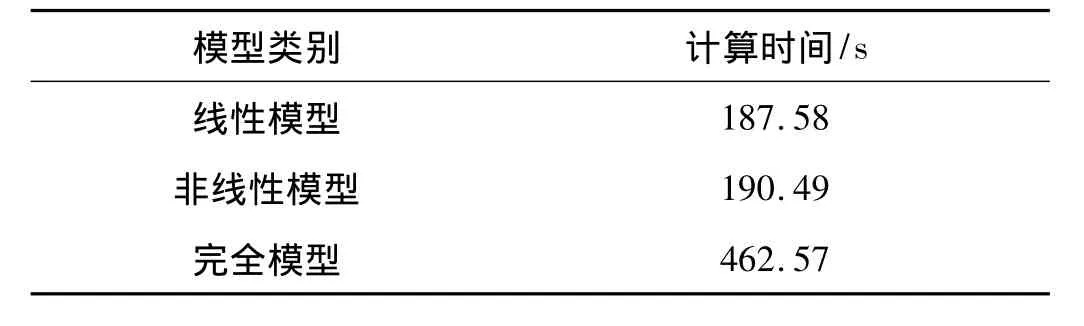
表2 三種模型的仿真計算時間對比Tab.2 The simulation time of the three models

4 結論

首先建立了三種空氣彈簧動力學模型的數學表達式，包括線性模型、非線性模型和完全模型。以車輛動力學的仿真結果對空氣彈簧施加激勵，對三種模型進行準靜態仿真，研究了三種模型動態特性的差異。最后將三種模型引入高速動車組的整車動力學模型，并進行動力學仿真計算，以不同的空氣彈簧建模方法對高速動車組進行了動力學特性分析。通過上述研究，主要可以得出以下結論:

(1)在準靜態仿真中，非線性模型與完全模型的回滯曲線較接近，其二者回滯曲線兩端較尖扁，體現了空氣彈簧的非線性特性，而線性模型的回滯曲線呈橢圓形且阻尼特性較高;

(2)在整車動力學計算中，三種模型計算的車輛運行安全性指標差異不大，非線性模型與完全模型的相對誤差在2%以內，線性模型與完全模型的相對誤差在4%以內;

(3)三種模型對車輛的垂向平穩性指標影響較大，完全模型和非線性模型在250 km/h－300 km/h速度級間會呈現非線性特性，而線性模型的垂向平穩性指標呈線性變化;

(4)考慮到三種模型的計算速度，非線性模型與線性模型的計算速度相差不大，且比完全模型快2.5倍左右，因此在高速動車組的動力學工程計算中建議采用非線性模型。

［1］Oda N，Nishimura S.Vibration of air suspension bogie and their design［C］.Bull.JSME，1970，13(55):43 －50.

［2］Krettek O，Grajnert J.Die modelldarstellung pneumatischer fahrzeugfederungen und die vorauswahl der modellparameter［J］.ZEV+DET Glas.Ann，1991，115(5):142 －145.

［3］Nieto A J，Morales A L，Gonzalez A，et al.An analytical model of pneumatic suspensions［J］.Veh.Syst.Dyn，2007 45(6):505－524.

［4］Doquier N.Multiphysics modeling of multibody systemsapplication to railway pneumatic suspension［D］.Universite Catholique de Louvain，November，2010.

［5］Quaglia G，Sorli M.Air suspension dimensionless analysis and design procedure［J］.Veh.Syst.Dyn，2001，35(6):443－475.

［6］孔軍.空氣彈簧在我國軌道車輛中的應用與發展［J］.鐵道車輛，2002:40(2):5－8.KONG Jun.Application and development of air springs for rail cars in our country［J］.Rolling Stock，2002:40(2):5－8.

［7］李芾，付茂海，黃運華.空氣彈簧動力學特性參數分析［J］.西南交通大學學報，2003，38(3):276－281.LI Fu，FU Mao-hai，HUANG Yun-hua.Analysis of dynamic characteristic parameterofairspring［J］. Journalof Southwest Jiaotong University，2003，38(3):276－281.

［8］張廣世，沈鋼.帶有連接管路的空氣彈簧動力學模型研究［J］.鐵道學報，2005，27(4):36－41.ZHANG Guang-shi，SHEN Gang.Study on dynamic airspring model with connecting pipe［J］.Journal of the China Railway Society，2005，27(4):36－41.

［9］張利國，張嘉鐘，賈力萍等.空氣彈簧的現狀及其發展［J］.振動與沖擊，2007，26(2):146－151.ZHANG Li-guo， ZHANG Jia-zhong， JIA Li-ping et al.Future and development of air springs［J］.Journal of Vibration and Shock，2007，26(2):146－151.

［10］王家勝，朱思洪.帶附加氣室空氣彈簧動剛度的線性化模型研究［J］.振動與沖擊，2009，28(2):72－76.WANG Jia-sheng， ZHU Si-hong. Linearizedmodelfor dynamic stiffness of air spring with auxiliary chamber［J］.Journal of Vibration and Shock，2009，28(2):72－76.

［11］李鵬，楊翊仁，魯麗.氣動力作用下高速車輛橫向穩定性分析［J］.振動與沖擊，2010，29(11):135－138.LI Peng，YANG Yi-ren，LU Li.Lateral stability of a highspeed train under aerodynamic force［J］.Journal of Vibration and Shock，2010，29(11):135－138.

［12］TB/T 2841—2005.中華人民共和國鐵道行業標準，鐵道車輛空氣彈簧［S］，鐵道部標準計量研究所，2005.

［13］中華人民共和國鐵道部，高速動車組整車試驗規范［S］.北京，2008.