集成相對位移自傳感磁流變阻尼器性能優(yōu)化

白先旭，王代華

(1. 重慶大學(xué) 光電工程學(xué)院，重慶 400030；2. 重慶大學(xué) 光電技術(shù)及系統(tǒng)教育部重點實驗室，重慶 400030)

目前，磁流變(Magnetorheological, MR)阻尼器的可控阻尼性能及應(yīng)用該半主動可控器件系統(tǒng)性能被優(yōu)化已獲得廣泛認(rèn)可。而為充分利用MR阻尼器可控阻尼性能，半主動系統(tǒng)需安裝與主動系統(tǒng)相同動態(tài)響應(yīng)傳感器[1]。不僅降低基于MR阻尼器的半主動系統(tǒng)可靠性，且使系統(tǒng)結(jié)構(gòu)復(fù)雜化、增加安裝空間、提高系統(tǒng)成本。對此，實現(xiàn)具有動態(tài)響應(yīng)自傳感功能的MR阻尼器勢在必行。Wang等[2]提出并研究集成相對位移自傳感MR阻尼器(IRDSMRD)，而研究中發(fā)現(xiàn)，IRDSMRD雖能實現(xiàn)相對位移傳感功能與可控阻尼力功能的集成，但為實現(xiàn)在MR阻尼器中集成相對位移傳感器(IRDS)，IRDSMRD阻尼力性能會受影響[3-4]，隨用于IRDSMRD的勵磁電流增加，即隨IRDSMRD的阻尼力增加，IRDS傳感器輸出信號逐漸表現(xiàn)出非線性特性。

對IRDSMRD性能優(yōu)化，需對MR阻尼器性能及IRDS性能優(yōu)化。即IRDSMRD阻尼力與IRDS傳感性能應(yīng)協(xié)調(diào)優(yōu)化。MR阻尼器性能優(yōu)化主要對MR阻尼器幾何尺寸優(yōu)化。Rosenfeld等[5]對體積一定的MR阻尼器進(jìn)行結(jié)構(gòu)尺寸優(yōu)化且對不同功率密度對無量綱厚度與阻尼因子影響進(jìn)行研究。Nguyen等[6]對半主動懸架用MR阻尼器最大阻尼力、動態(tài)阻尼力范圍及感應(yīng)時間常數(shù)利用ANSYS軟件進(jìn)行優(yōu)化，給出對設(shè)計MR阻尼器有指導(dǎo)意義結(jié)論。而迄今鮮有阻尼力性能與IRDS性能同時優(yōu)化研究。設(shè)計、開發(fā)自傳感MR阻尼器時，如何優(yōu)化IRDSMRD相互影響的IRDS傳感性能及MR阻尼器可控阻尼力性能為須解決的問題。

實際上，將同時優(yōu)化IRDSMRD阻尼力性能與IRDS傳感性能可視為多目標(biāo)優(yōu)化問題[7]。Pareto優(yōu)化方法可用于尋找相互制約目標(biāo)的最優(yōu)協(xié)調(diào)。Paplia等[8-9]利用Pareto優(yōu)化圓形壓電執(zhí)行器體積量及共振頻率，并對壓阻麥克風(fēng)壓強(qiáng)靈敏度及電子噪聲底限進(jìn)行協(xié)調(diào)優(yōu)化。關(guān)新春等[10]用Pareto對MR阻尼器的阻尼力及動態(tài)阻尼力范圍進(jìn)行協(xié)調(diào)優(yōu)化。由此，Pareto優(yōu)化方法可用于IRDSMRD阻尼力與IRDS傳感性能優(yōu)化。據(jù)文獻(xiàn)[3]，IRDSMRD阻尼力及IRDS線性度同時優(yōu)化可通過優(yōu)化IRDSMRD結(jié)構(gòu)參數(shù)實現(xiàn)，亦可通過降低作用于IRDSMRD的勵磁電流(對同一IRDSMRD而言即為作用磁動勢)實現(xiàn)。Wang等[4]通過優(yōu)化IRDSMRD結(jié)構(gòu)參數(shù)實現(xiàn)對IRDSMRD的最大可控阻尼力及IRDS線性度協(xié)調(diào)優(yōu)化。本文為對IRDSMRD性能(阻尼力性能、IRDS傳感性能)優(yōu)化，提出基于Pareto優(yōu)化原理、對體積一定的IRDSMRD關(guān)鍵參數(shù)(含結(jié)構(gòu)參數(shù)及作用磁動勢)進(jìn)行關(guān)于目標(biāo)函數(shù)為阻尼力及IRDS的線性度優(yōu)化方法。對影響IRDSMRD阻尼力與IRDS線性度的磁通回路磁特性建模、分析并建立受IRDSMRD關(guān)鍵參數(shù)影響的IRDS線性度與IRDSMRD阻尼力數(shù)學(xué)模型，并利用Pareto優(yōu)化原理對IRDSMRD性能協(xié)調(diào)優(yōu)化。

1 IRDSMRD的原理與數(shù)學(xué)模型

1.1 IRDSMRD的結(jié)構(gòu)與原理

文獻(xiàn)[2]的IRDSMRD結(jié)構(gòu)原理與3D拆裝分別見圖1(a)、(b)。IRDSMRD電路系統(tǒng)原理示意及系統(tǒng)實物分別見圖2(a)、(b)。IRDSMRD結(jié)構(gòu)材料屬性與基本參數(shù)見表1。由圖1，IRDSMRD利用在高導(dǎo)磁活塞上均勻繞制勵磁線圈同時充當(dāng)MR阻尼器的勵磁線圈及IRDS的勵磁線圈，利用在不導(dǎo)磁的缸筒上均勻繞制感應(yīng)線圈作為IRDS感應(yīng)線圈，置于高導(dǎo)磁缸體罩內(nèi)。由圖2、表1，通過疊加電路將勵磁電流與載波信號疊加后作用于IRDSMRD活塞的勵磁線圈，產(chǎn)生直流勵磁磁場及與載波信號同頻的諧波磁場疊加磁場，并沿IRDSMRD主磁通回路閉合。由勵磁線圈產(chǎn)生的磁場使缸體罩內(nèi)不導(dǎo)磁缸體上均勻繞置的感應(yīng)線圈獲得感應(yīng)電壓，該電壓由與載波信號同頻的諧波電壓信號及勵磁電流作用于運動的活塞上勵磁線圈產(chǎn)生的直流勵磁場而產(chǎn)生的感應(yīng)信號兩部分組成。當(dāng)活塞相對缸體運動時，感應(yīng)線圈中諧波電壓信號被活塞與缸體間相對位移實現(xiàn)幅度調(diào)制。通過解調(diào)感應(yīng)線圈的感應(yīng)電壓可獲得活塞相對缸體位移，實現(xiàn)IRDS。由于MR液流間隙位于主磁通回路中，由勵磁電流產(chǎn)生的磁場將對MR阻尼器實現(xiàn)勵磁，即實現(xiàn)MR阻尼器與動態(tài)傳感器功能集成。

為確保IRDSMRD具有較好的阻尼力性能及位移傳感性能，所選材料應(yīng)確保IRDSMRD勵磁磁場起于阻尼器活塞、穿過MR液流間隙、缸體及感應(yīng)線圈，沿高導(dǎo)磁缸體罩、上端蓋、活塞桿，返回活塞形成的閉合工作磁回路(即主磁通回路)。為使磁場盡量能沿主磁通回路，活塞桿、活塞頭、上端蓋、缸體罩選高導(dǎo)磁率的金屬軟磁材料(20#鋼)，而缸體、勵磁線圈蓋及缸體下端蓋選不導(dǎo)磁的金屬材料(不銹鋼)，材料屬性見表1。

圖1 IRDSMRD原理與結(jié)構(gòu)

圖2 IRDSMRD電路系統(tǒng)

表1 IRDSMRD結(jié)構(gòu)材料磁特性及參數(shù)值

1.2 IRDSMRD數(shù)學(xué)模型

1.2.1磁通回路模型

IRDSMRD磁通回路及等效磁路模型見圖3，其中各符號含義及尺寸見表2。

據(jù)磁路Kirchhoff第二定理得：

PI=NI=φIR

(1)

式中：PI為由幅值為I的勵磁電流作用于匝數(shù)為N的勵磁線圈產(chǎn)生的磁動勢；φI為磁動勢PI在磁通回路中產(chǎn)生的總磁通量；R為主磁通回路總磁阻，據(jù)圖3，R可表示為

R=Rr1+Rl2+Rh+RL+Rg1+Rg2+Rg3

(2)

式中：Rr1，Rl2，Rh,RL,Rg1，Rg2，Rg3為在IRDSMRD主磁通回路中活塞桿、上端蓋、缸體罩、活塞頭、MR液流間隙(對應(yīng)于活塞頭高度)、不導(dǎo)磁缸體及感應(yīng)線圈磁阻，可分別表示為

(3)

式中：μ0為真空磁導(dǎo)率(表1)；x(t)為活塞相對缸體位移，起點為IRDSMRD行程零點(圖1(a)、圖3(a))；l1，l2，L分別為勵磁線圈蓋高度、上端蓋厚度、活塞頭高度；r1，r2，rp分別為活塞桿半徑、中心孔半徑、活塞頭半徑；g1，g2，g3分別為圓環(huán)形液流間隙厚度、缸體厚度、感應(yīng)線圈厚度；h為缸體罩厚度；μr1，μl2，μh,μL,μg1，μg2，μg3分別為活塞桿、上端蓋、缸體罩、活塞頭、MR液流間隙(對應(yīng)于活塞頭高度)、不導(dǎo)磁缸體及感應(yīng)線圈磁導(dǎo)率。本文將不導(dǎo)磁缸體及感應(yīng)線圈磁導(dǎo)率近似于空氣，即μg2=μg3=μair=1。

磁動勢PI在IRDSMRD磁通回路中產(chǎn)生的總磁通量φI可表示為

φI=BaAa

(4)

式中：Aa為主磁通回路中任意處截面積；Ba為Aa處磁感應(yīng)強(qiáng)度。

據(jù)文獻(xiàn)[4]及式(2)、(3)，金屬軟磁性材料(20#鋼)磁導(dǎo)率隨磁動勢PI的變化微小變化。據(jù)式(4)、表2可得活塞桿、上端蓋、缸體罩、活塞頭及MR液流間隙處MR液磁感應(yīng)強(qiáng)度及磁導(dǎo)率μr1，μl2，μh，μL，μg1。

圖3 IRDSMRD電磁回路

表2 IRDSMRD結(jié)構(gòu)尺寸

1.2.2 IRDS線性度

IRDS傳感器所得信號與感應(yīng)線圈上感應(yīng)諧波電壓e1(t)相關(guān)[3]。據(jù)IRDSMRD原理，載波信號作用于IRDSMRD勵磁線圈上，在感應(yīng)線圈上被激活的磁鏈總數(shù)ψc(t)可表示為

(5)

式中：φc(t)為載波信號Vc在IRDSMRD主磁通回路產(chǎn)生的主磁通量；k為IRDSMRD缸體單位長度上繞感應(yīng)線圈匝數(shù)；Pc為載波信號作用于IRDSMRD勵磁線圈產(chǎn)生的磁動勢。

感應(yīng)線圈上磁通量為余弦信號較載波信號提前π/2[2]，有：

(6)

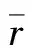
對式(6)兩端微分得IRDSMRD感應(yīng)線圈上感應(yīng)諧波電壓e1(t)為

(7)

據(jù)調(diào)制解調(diào)原理，在式(7)兩端同乘參考信號得：

(8)

對式(8)信號低通濾除頻率2fc信號(圖2(a))，得：

(9)

據(jù)文獻(xiàn)[4]及式(1)～式(3)，IRDSMRD磁通回路總磁阻R在磁動勢PI影響下發(fā)生輕微變化。因此，由式(9)可知解調(diào)后信號Edis會受IRDSMRD主磁通回路磁阻R及IRDSMRD活塞位移量x(t)影響。而相對位移量x(t)對Edis影響無法避免。為IRDS原理誤差，且相對總磁阻R對Edis影響而言較小，本文忽略x(t)變化對Edis影響。定義IRDS線性度(即非線性誤差)為

(10)

式中：E0為主磁通回路各處磁導(dǎo)率均為初始值時相對位移，即Edis初始值。

據(jù)式(1)～式(3)、(9)、(10)，IRDS線性度會受作用于IRDSMRD上磁動勢及IRDSMD磁通回路上結(jié)構(gòu)參數(shù)影響。據(jù)式(9)，式(10)可改寫為

(11)

式中：R0為主磁通回路初始總磁阻，與E0對應(yīng)。

對IRDS線性度產(chǎn)生影響的關(guān)鍵參數(shù)為IRDSMRD活塞頭高度L[4]。據(jù)式(1)～式(3)，作用于IRDSMRD上磁動勢即為導(dǎo)致IRDS非線性主要原因，本文設(shè)作用于IRDSMRD上勵磁電流最大值已確定，即磁動勢PI為IRDSMRD活塞上繞勵磁線圈匝數(shù)N已確定。因此，可定義向量X=[N,L]T為決定IRDS線性度主要變量。

1.2.3 阻尼力

IRDSMRD阻尼力由粘滯阻尼力與 MR液流間隙受磁場作用產(chǎn)生的剪切屈服應(yīng)力(即場控阻尼力)組成[11]，由圖1、圖3(a)，IRDSMRD阻尼力可表示為

(12)

剪切-有效磁感應(yīng)強(qiáng)度Bg1可表示為

(13)

式中：φg1為主磁通量。考慮MR液流間隙附近存在磁力線擴(kuò)散，存在近似關(guān)系：

φg1≈0.45φl

(14)

據(jù)文獻(xiàn)[4]及式(12)，IRDSMRD阻尼力主要由活塞頭高度L與導(dǎo)致MR液產(chǎn)生剪切屈服力的磁動勢PI決定。最大勵磁電流一定時，磁動勢PI由IRDSMRD活塞上所繞勵磁線圈匝數(shù)N確定。因此向量X=[N,L]T可決定IRDSMRD的可控阻尼力變量。

1.3 數(shù)值仿真

據(jù)上述，因其它參數(shù)(上端蓋厚度、缸體外罩厚度)對IRDS線性度影響及阻尼力影響有限，而活塞桿半徑(纏繞勵磁線圈部分)及活塞頭高度為主要影響因素，其中活塞桿半徑對阻尼力、IRDS線性度而言越大越好，故取上限(13.0 mm)。本文在不同活塞頭高度L、勵磁線圈匝數(shù)N對阻尼力及IRDS線性度影響程度進(jìn)行數(shù)值仿真。具有不同勵磁線圈匝數(shù)N及活塞頭高度L時IRDSMRD阻尼力性能及IRDS傳感器性能數(shù)值仿真結(jié)果見圖4。由圖4看出，勵磁線圈匝數(shù)N恒定時，隨活塞頭高度L逐漸增加，IRDSMRD阻尼力亦逐漸增加，IRDS線性度逐漸惡化；活塞頭高度L恒定時，隨勵磁線圈匝數(shù)N逐漸增加，IRDSMRD阻尼力逐漸增加，而IRDS線性度逐漸惡化。因此可認(rèn)為，通過優(yōu)化IRDSMRD關(guān)鍵參數(shù)優(yōu)化阻尼力性能(或IRDS傳感性能)時，IRDSMRD的IRDS傳感性能及阻尼力性能相互制約。

由圖4看出，勵磁線圈匝數(shù)N、活塞頭高度L同超一定范圍時，N與L對IRDSMRD性能產(chǎn)生條件限制，此時無解。

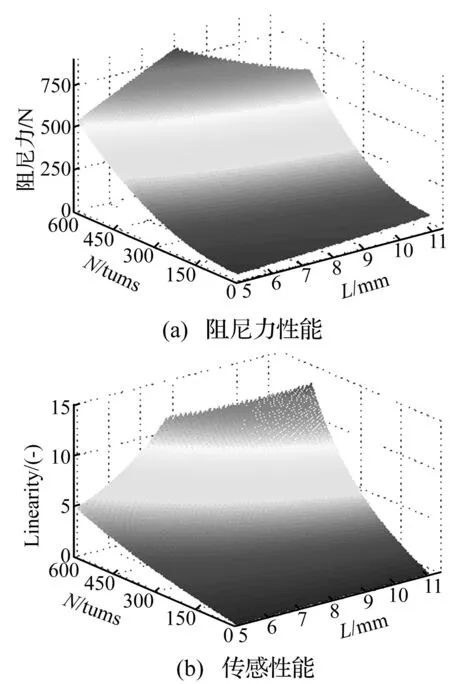
圖4 不同勵磁線圈匝數(shù)、活塞頭高度時IRDSMRD性能

2 優(yōu)化設(shè)計

IRDSMRD最大可控阻尼力與IRDS線性度優(yōu)化可通過優(yōu)化IRDSMRD關(guān)鍵結(jié)構(gòu)參數(shù)實現(xiàn)，也可通過降低作用于IRDSMRD的磁動勢(即在最大勵磁電流一定時優(yōu)化勵磁線圈匝數(shù)N)實現(xiàn)[3]。而通過優(yōu)化IRDSMRD的關(guān)鍵結(jié)構(gòu)參數(shù)實現(xiàn)對IRDSMRD最大可控阻尼力、IRDS線性度協(xié)調(diào)優(yōu)化[4]。本文通過優(yōu)化IRDSMRD作用磁動勢PI與活塞頭高度L實現(xiàn)對目標(biāo)函數(shù)分別為IRDSMRD最大可控阻尼力、IRDS線性度協(xié)調(diào)優(yōu)化。

2.1 設(shè)計變量

由于IRDSMRD最大可控阻尼力、IRDS線性度均關(guān)于勵磁線圈匝數(shù)N(作用于IRDSMRD電流I最大值為定值時)、活塞頭高度L函數(shù)且之間存在相互約束關(guān)系，采用Pareto優(yōu)化對二者協(xié)調(diào)優(yōu)化。在作用于IRDSMRD電流I最大值為定值時優(yōu)化IRDSMRD阻尼力及IRDS傳感性能，取優(yōu)化變量為勵磁線圈匝數(shù)N及活塞頭高度L，即向量X=[N,L]T為優(yōu)化變量。

2.2 約束條件

優(yōu)化參數(shù)邊界及操作要求為

(1) 設(shè)計變量下邊界(LB)、上邊界 (UB)：考慮IRDSMRD實際尺寸，設(shè)計變量邊界可表示為

XLB

(15)

式中：XLB=[0.5]T，XUB=[60 011]T為IRDSMRD優(yōu)化變量最小、最大值。

(2) 磁感應(yīng)強(qiáng)度：IRDSMRD選材的磁感應(yīng)強(qiáng)度所受約束可表示為

(16)

式中：BsMRF，Bs20分別為MR液、20#鋼飽和磁感應(yīng)強(qiáng)度；Ba20為IRDSMRD結(jié)構(gòu)零件(20#鋼，表1)。

(3) 勵磁電流(I)：作用于IRDSMRD的勵磁線圈上電流最大為1.2 A，即

(17)

2.3 表達(dá)式

優(yōu)化問題可視為優(yōu)化目標(biāo)函數(shù)FO(X)，表示為

(18)

2.4 Pareto優(yōu)化

實現(xiàn)IRDSMRD阻尼力最大化目標(biāo)的同時，IRDS線性度會降低，即實現(xiàn)IRDSMRD阻尼力最大化目標(biāo)與實現(xiàn)IRDS線性度最優(yōu)目標(biāo)相互制約。若不考慮IRDS線性度約束，IRDSMRD阻尼力可被提高至較大范圍(IRDS線性度較差)。IRDS線性度亦為IRDSMRD重要性能，故將IRDS線性度與IRDSMRD阻尼力考慮為多目標(biāo)函數(shù)優(yōu)化問題較正確。

Pareto優(yōu)化常被用于多目標(biāo)優(yōu)化，為典型的尋找能使每個函數(shù)均在約束條件內(nèi)的最優(yōu)折中方法。稱多目標(biāo)優(yōu)化問題Pareto最優(yōu)解在目標(biāo)函數(shù)空間中的表現(xiàn)形式為Pareto最優(yōu)邊界(Pareto前沿)。對相互約束的多目標(biāo)函數(shù)，在Pareto前沿找不到能使所有目標(biāo)變好的解。為同時優(yōu)化IRDSMRD阻尼力及IRDS傳感性能，利用Pareto優(yōu)化方法原理，據(jù)式(18)構(gòu)建總體目標(biāo)函數(shù)f1=F(X)并增加限制其它目標(biāo)函數(shù)fj=γ(X)的函數(shù)Cj=γlimj(X)(為不同IRDS線性度預(yù)置值)以評價多目標(biāo)函數(shù)特性，可寫為

(19)

通過用不同Cj獲得Pareto最優(yōu)點集(即在除去此點之外找不到能使目標(biāo)函數(shù)更優(yōu)的點)，從而獲得Pareto前沿。

3 結(jié)果與討論

利用MATLAB軟件對IRDSMRD阻尼力及IRDS線性度進(jìn)行關(guān)于向量X(即參數(shù)N，L)在上下邊界內(nèi)等間距逐點計算，結(jié)果見圖5。由圖5看出，所有Pareto最優(yōu)解組成Pareto前沿。該前沿上PO1點為典型解，即IRDS線性度最優(yōu)解，IRDSMRD阻尼力較小。Pareto前沿上PO3點也為典型解，即IRDSMRD最大阻尼力及較差I(lǐng)RDS線性度。PO2點在PO1點與PO3點之間。PN4點為PO1點水平延長線與PO2點垂線交點。PN3點為PO2點水平延長線與PO3點垂線交點。PN2點在PO2點垂線上，位于PO2點與PN4點之間。PN1點在PO2點水平線上，位于PO2點與PN3點之間。顯然，PN1點與PN2點不在Pareto前沿，均為非Pareto最優(yōu)解，而PN3點，PN4均非解。Pareto最優(yōu)解在PO1，PO2，PO3點，相應(yīng)IRDSMRD關(guān)鍵參數(shù)見表3。由于非Pareto最優(yōu)解對應(yīng)多組參數(shù)(L，N)，表3只列出在PN1點、PN2點的非Pareto最優(yōu)解結(jié)果，未列出參數(shù)組合。而PN3，PN4點為非解，故未給參數(shù)值。由表3、圖5知，PO1點最優(yōu)解表明通過優(yōu)化參數(shù)可使IRDSMRD線性度優(yōu)化為0.09%，而阻尼力降至99 N。PO3點最優(yōu)解表明通過優(yōu)化結(jié)構(gòu)參數(shù)可使IRDSMRD阻尼力優(yōu)化為804 N，而線性度惡化為11.3%。兩解均為極端解，優(yōu)化的以惡化為代價。

表3 Pareto最優(yōu)解、結(jié)構(gòu)參數(shù)及非Pareto最優(yōu)解

實際上，關(guān)于阻尼力及IRDS線性度滿意解可從Pareto前沿選取，如在PO1，PO3點之間。Pareto前沿上PO2點為IRDSMRD最優(yōu)解，阻尼力為528.9 N，IRDS線性度為4.4%，與其對應(yīng)的關(guān)鍵參數(shù)值見表3。而PN2，PN4點均不在Pareto前沿但具有與PO2相同的線性度卻達(dá)不到PO2點阻尼力。即使PN4點的解能達(dá)到PO1點阻尼力，但PN4點IRDS線性度較PO1點線性度差的多。對不在Pareto前沿的點PN1，PN3，雖阻尼力與PO2點相同，卻無PO2點IRDS線性度。PN3點IRDS線性度雖與PO3相同，但PN3點阻尼力卻較PO3點差。因此可認(rèn)為，在Pareto前沿的點均為最大阻尼力及IRDS線性度最優(yōu)解，二者不可能同時提高，即一個目標(biāo)優(yōu)化必將削弱另一目標(biāo)。

圖5 N與L優(yōu)化時所得最大阻尼力與線性度關(guān)系及Pareto最優(yōu)邊界

4 結(jié) 論

本文提出、研究并實現(xiàn)基于Pareto優(yōu)化原理針對目標(biāo)函數(shù)為IRDSMRD的阻尼力及IRDS線性度優(yōu)化關(guān)鍵參數(shù)方法。對直接影響IRDSMRD阻尼力性能及IRDS傳感性能的主磁通回路進(jìn)行磁路建模與分析，并建立受磁動勢與IRDSMRD結(jié)構(gòu)參數(shù)影響的IRDS線性度數(shù)學(xué)模型、IRDSMRD阻尼力模型。結(jié)論如下：

(1) 通過優(yōu)化，當(dāng)IRDSMRD體積一定時，可得IRDSMRD阻尼力性能與IRDS傳感性能間關(guān)系的Pareto最優(yōu)曲線(即Pareto前沿)。

(2) 不考慮IRDSMRD的IRDS線性度約束時，IRDSMRD阻尼力可為較大值(804 N)，但此時IRDS傳感性能較差(11.3%)；而不考慮IRDSMRD阻尼力約束時，IRDS線性度會較好(0.09%)，此時阻尼力亦較小(99 N)。

(3) 用本文關(guān)于IRDSMRD阻尼力及IRDS線性度均為最優(yōu)的Pareto前沿，可實現(xiàn)對不同應(yīng)用要求的IRDSMRD性能進(jìn)行活塞頭高度與勵磁線圈匝數(shù)的協(xié)調(diào)設(shè)計。Pareto前沿對IRDSMRD設(shè)計具有一定指導(dǎo)意義。基于Pareto優(yōu)化原理實現(xiàn)IRDSMRD兩種性能間協(xié)調(diào)優(yōu)化方法表明，該方法在基于智能材料自傳感執(zhí)行器的優(yōu)化中存在普遍性。

[1]Wang D H,Liao W H.Semiactive controllers for magnetorheological fluid dampers[J].Journal of Intelligent Material Systems and Structures, 2005, 16(11/12):983-993.

[2]Wang D H,Wang T.Principle, design and modeling of an integrated relative displacement self-sensing magnetorheological damper based on electromagnetic induction[J].Smart Materials and Structures,2009,18(9): 095025-095044.

[3]Wang D H, Bai X X,Liao W H, An integrated relative displacement self-sensing magnetorheological damper: prototyping and testing[J].Smart Materials and Structures, 2010, 19(10): 105008-105026.

[4]Wang Dai-hua,Bai Xian-xu.Pareto optimization based tradeoff between the damping force and the sensed relative displacement of a self-sensing magnetorheological damper[J]. Journal of Intelligent Material Systems and Structures, 2011, 22(13): 1451-1467.

[5]Rosenfeld N C,Wereley N M.Volume-constrained optimization of magnetorheological and electrorheological valves and dampers[J].Smart Materials and Structures, 2004, 13(6): 1303-1313.

[6]Nguyen Q H,Choi S B.Optimal design of a vehicle magnetorheological damper considering the damping force and dynamic range[J].Smart Materials and Structures, 2009, 18(1): 015013-015022.

[7]韓民春.西方經(jīng)濟(jì)學(xué) (第二部分: 微觀經(jīng)濟(jì)學(xué)) [M].北京: 北京大學(xué)出版社, 2007:273-280.

[8]Papila M, Sheplak M,Cattafesta III L N.Optimization of clamped circular piezoelectric composite actuators[J].Sensors and Actuators A: Physical, 2008, 147(1):310-323.

[9]Papila M, Haftka R T, Nishida T, et al. Piezoresistive microphone design pareto optimization: tradeoff between sensitivity and noise floor[J].Journal of Microelectromechanical Systems, 2006, 15(6): 1632-1643.

[10]關(guān)新春, 郭鵬飛, 歐進(jìn)萍.磁流變阻尼器的多目標(biāo)優(yōu)化設(shè)計與分析[J].工程力學(xué), 2009, 26(9): 30-35.

GUAN Xin-chun, GUO Peng-fei, OU Jin-ping.Multi-objective optimization of magnetorheological fluid dampers[J]. Engineering Mechanics, 2009, 26(9):30-35.

[11]Wang D H, Wang T, Bai X X, et al. A self-sensing magnetorheological shock absorber for motorcycles[C]. Proceedings of 19thInternational Conference on Adaptive Structures and Technologies, Ascona, Switzerland, 2008.

[12]Ashour O, Rogers C A,Kordonsky W I.Magnetorheological fluids: materials, characterization, and devices[J].Journal of Intelligent Material Systems and Structures,1996,7(2):123-130.