起伏噪聲中單矢量傳感器預警檢測方法

郭虎生，顏 冰

(海軍工程大學 兵器工程系,武漢 430033)

在海洋環境噪聲背景中探測識別目標的前提是實現對目標信號的可靠檢測。傳統的水中目標預警檢測方法有能量檢測、過零檢測、功率譜線譜檢測等。其中能量檢測方法(ED)為水中目標預警檢測中常用方法[1]，用信號加噪聲的功率級與噪聲功率級(或幅度)不同特點檢測輸入信號幅度均值變化。該方法實現簡單，可長時間噪聲背景中檢測微弱目標信號，但對環境噪聲幅度起伏敏感，抗起伏背景干擾能力差。

為增加探測距離及可靠性，需尋求更低信噪比下有效檢測微弱目標信號技術。本文在矢量傳感器抑制各向同性噪聲基礎上提出利用多通道采樣數據構造協方差矩陣，并以最大與最小特征值之比為檢驗統計量進行目標判決的信號檢測方法。該方法可在低信噪比及環境噪聲變化條件下實現目標可靠監測。

1 能量檢測原理及起伏噪聲影響

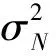
(1)

能量檢測作為目前對未知確定性信號的最有效檢測算法，通過計算時間帶寬積內的信號能量與預先設定的門限比較，獲得檢測結果。判決統計量Y為

(2)

式中：N為檢測信號取樣點數。目標不存在時，判決統計量Y服從自由度為N的中心卡方分布，相反則服從自由度N的非中心卡方分布；采樣點數N增大時，判決統計量近似高斯隨機過程，即

(3)

同時可得檢測概率Pd及虛警概率Pf分別為

(4)

(5)

式中：γ為檢測判決門限；Q為標準高斯互補累積函數；能量檢測通常按所給虛警概率Pf求得判決門限：

(6)

由式(6)看出，判決門限與數據長度、噪聲功率有關，而海洋環境噪聲受多因素影響，噪聲功率會隨環境變化在一定范圍內變化，具有不確定特性。進一步假設環境噪聲變化范圍為

(7)

式中：p為噪聲起伏度。

能量檢測具有局限性：① 信噪較低時信號淹沒在噪聲中，能量檢測不能有效判決信號是否存在；② 絕對門限由噪聲功率、數據長度決定；③ 能量檢測只計算信號能量，不能區分信號、噪聲及干擾，不利于有效判決。

2 協方差檢測原理

2.1 構造檢測統計量

由矢量傳感器接收的各通道數據所得采樣協方差矩陣可分解為目標信號子空間與噪聲子空間，H1時對接收信號構成的協方差矩陣分解可得最大特征值，對應目標信號成份，最小特征值對應接收信號噪聲成份；H0時最大最小特征值均對應噪聲成份。因此，據接收信號的協方差矩陣在H1情況下最大最小特征值之比大于H0的特征值之比原理構建檢測判決量，為判斷目標的存在與否提供依據。協方差檢測充分利用矢量傳感器各通道接收信號時具有的相關性，噪聲在各通道無相關性，克服能量檢測只計算信號能量，不能區分信號、噪聲缺點的協方差檢測具有較低算法復雜度，且在噪聲變化時同樣可保持較高的檢測概率[2]。協方差檢測流程見圖1。

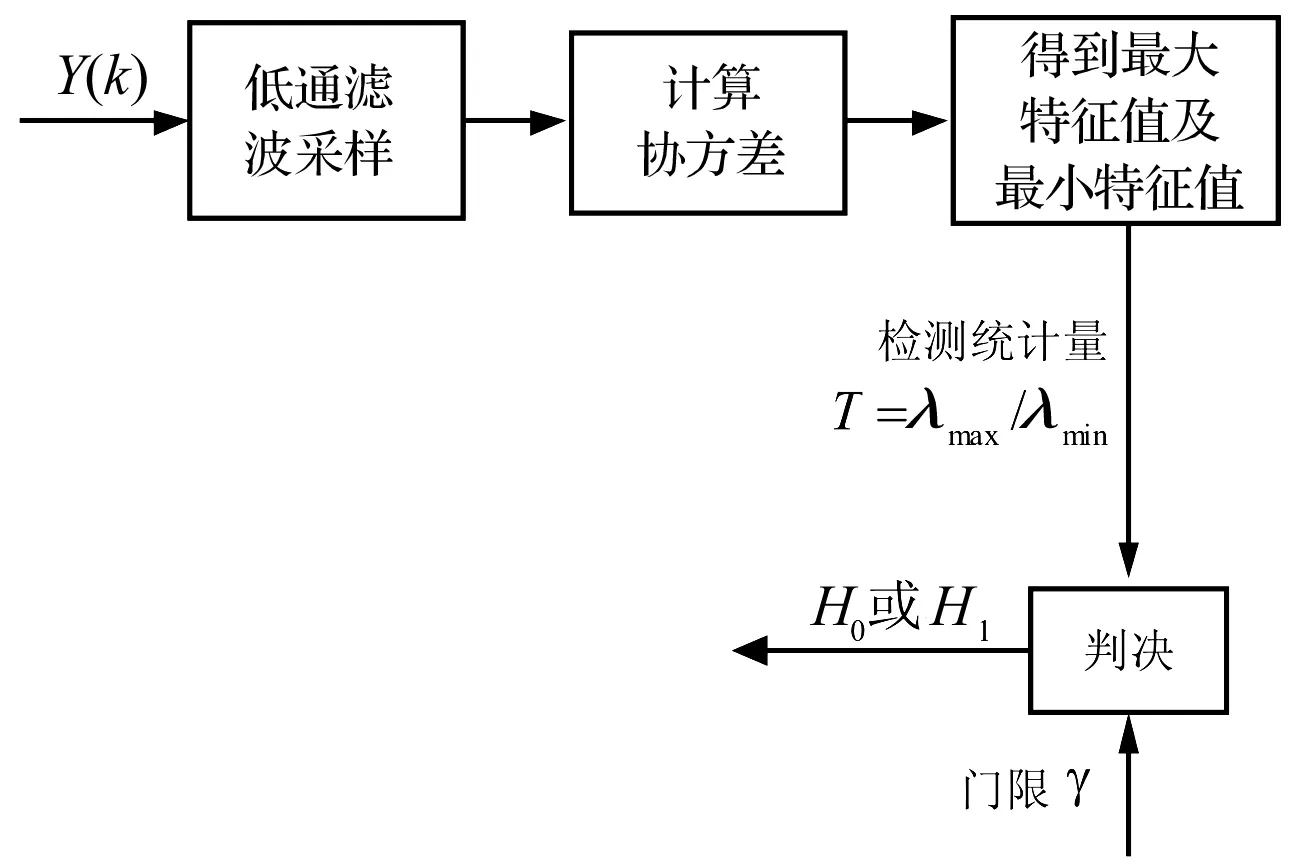
圖1 協方差檢測流程

航行中艦船部分聲能與海底耦合以海底界面波的形式傳播，稱艦船地震波，因其獨特的頻率及傳播特性可用于淺水環境的目標探測。三軸矢量傳感器布放于海底，可接收航行艦船的目標信息，其中各通道接收的噪聲信號可視為互不相關，而目標信號具有相關性[3-4]。若矢量傳感器由M個通道同時采樣，每個通道由N個連續采樣點組成，定義yi(k)為第i個采樣矢量中第k個采樣點值，則輸出振動分量為

(8)

通常目標信號與背景環境噪聲不相關，可求得接收信號協方差矩陣為

Ry=E[Y(k)YT(k)]=E[S(k)ST(k)]+

(9)

式中：I為M階單位矩陣。

H1時協方差矩陣含信號及噪聲能量，且分解所得最大特征值應對應信號能量，最小特征值代表噪聲能量；H0時只存在噪聲能量，可見兩種情況最大特征值λmax及最小特征值λmin比值不同。故本文采用最大與最小特征值之比構造檢驗統計量的協方差檢測方法(MMED)對信號進行預警檢測[5-7]，即

(10)

2.2 門限確定

實際中無法準確計算統計協方差，可由有限抽樣數據估計協方差矩陣

(11)

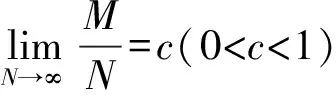
(12)

3 性能比較

3.1 數值仿真實驗

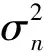
圖4為對兩種方法在信噪比-15 dB檢測性能隨采樣次數N變化的特性曲線。信噪比較低時，能量檢測方法的檢測概率較低，且隨采樣次數N的增加，檢測概率未提高；但噪聲起伏變化增大時，檢測性能嚴重下降，說明能量檢測無法通過增加采樣次數解決噪聲起伏所致影響。協方差檢測方法在低信噪比時檢測率較高，且隨采樣點數的增加，檢測概率提高較快，噪聲起伏變化對檢測性能影響較小，對噪聲起伏變化不敏感。

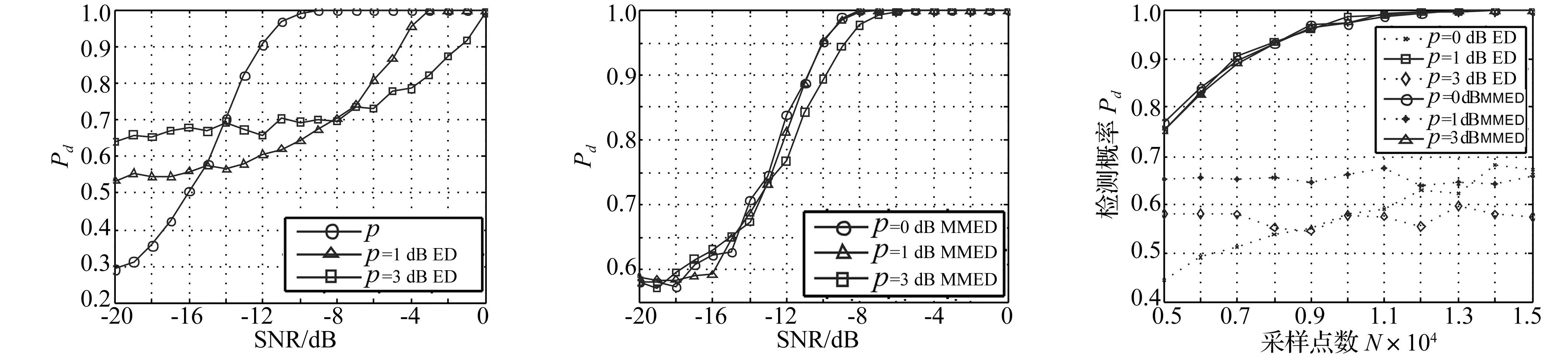
圖2 能量檢測性能曲線

3.2 測試數據分析

為進一步檢驗協方差檢測方法在實測環境中效果，用實測數據進行分析。在東海某海域進行海上實船實驗，水深20 m，淤泥質海底，實驗船只為大型船舶，用于接收數據的三軸地震波傳感器置于海底。實測目標的通過特性見圖5，采樣頻率fs=400 Hz，取時窗點數N=1 000；圖6為能量檢測與協方差檢測方法檢測結果。由圖6看出，協方差檢測方法性能高于能量檢測方法，尤其在低信噪比環境中信號幅度變化不明顯時，效果遠好于能量檢測方法，此由于協方差檢測方法可對噪聲、信號進行區別，能有效增強信號，使檢測性能明顯改善。

計算復雜度時，協方差檢測方法主要由計算采樣協方差及特征值分解構成，計算采樣協方差矩陣需NM次乘法、加法，特征值分解需O(M3)次，N遠大于M，該項可忽略不計。而能量檢測計算需N次乘法、加法，協方差檢測方法計算度為能量檢測的M倍，通道數不多時計算量并不復雜。

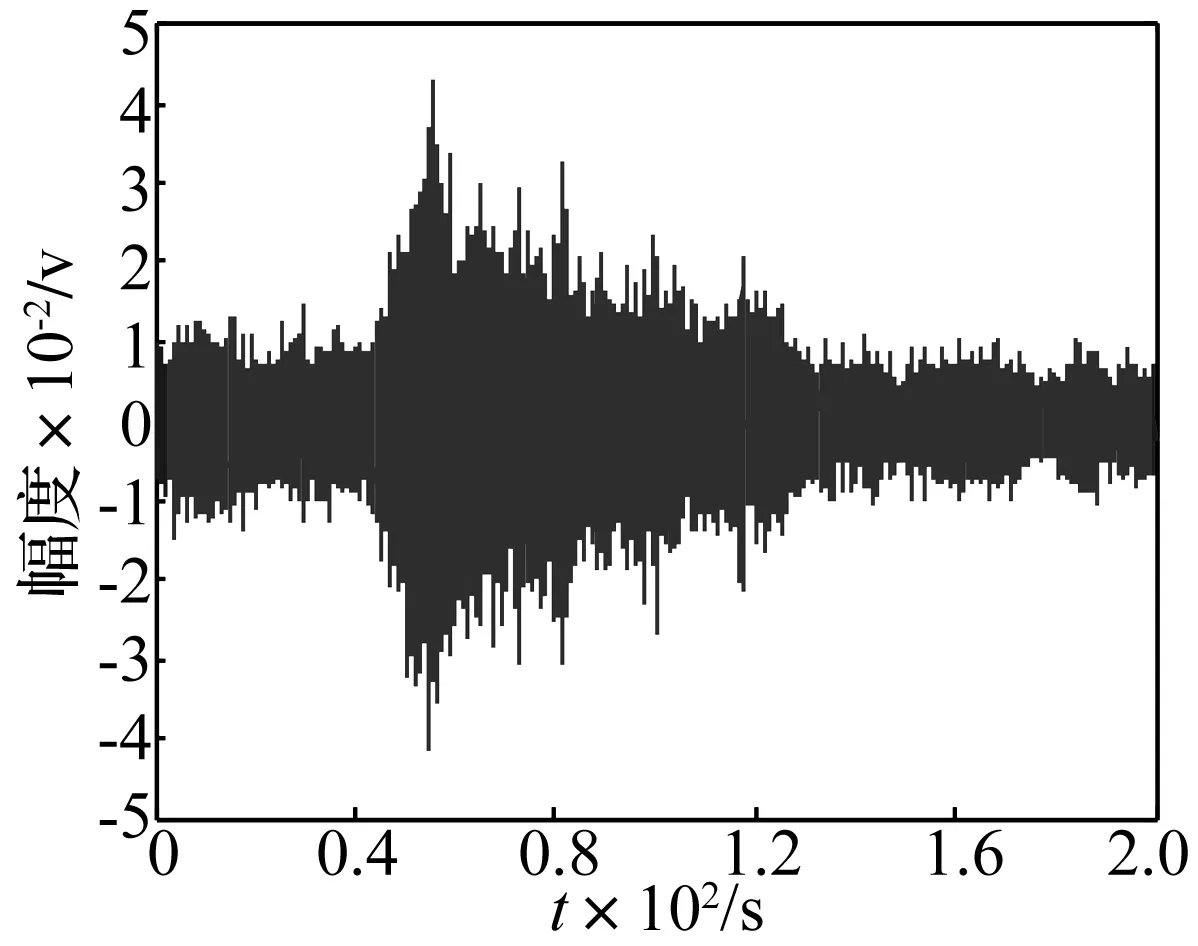
圖5 目標通過特性

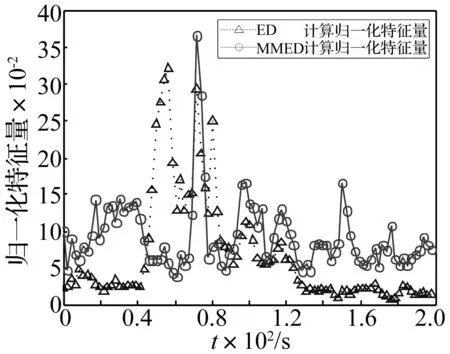
圖6 兩種方法特征量比較

4 結 論

本文在矢量傳感器抑制各向同性噪聲基礎上，利用接收數據的協方差矩陣特征值構建檢驗統計量對有無目標進行判決，改進了能量檢測方法統計量不能區分噪聲的缺陷。矢量傳感器具有抑制各向同性噪聲能力，可改善低信噪比環境下檢測性能。仿真及實驗表明，該方法在低信噪比下檢測性能優于能量檢測方法，且對噪聲變化不敏感，檢測精度較高，適合矢量傳感器目標的預警檢測。

[1]劉科滿，相敬林，侯鐵雙，等.基于目標過零特性與能量特性的聲引信檢測方法[J].兵工學報, 2008, 29(9): 1044-1048.

LIU Ke-man, XIANG Jing-lin, HOU Tie-shuang, et al. A joint method of zero-crossing detection and energy detection[J].Acta Armamentarii, 2008, 29(9): 1044-1048.

[2]Zeng Yong-hong, Liang Ying-chang.Eigenvalue based spectrum sensing algorithms for cognitive radio[J]. IEEE Trans. Communications,2009,57(6): 1784-1793.

[3]宋云飛，盧光躍. 基于采樣協方差矩陣的頻譜感知算法仿真分析[J]. 西安郵電學院學報, 2011, 16(5): 12-16.

SONG Yun-fei, LU Guang-yue. Simulation and analysis of spectrum sensing algorithms based on sample covariance matrix [J]. Journal of Xi’an University of Post And Telecommunications, 2011, 16(5):12-16.

[4]鄒吉武，孫大軍，呂云飛，等. 海洋矢量噪聲場試驗研究[J]. 哈爾濱工程大學學報,2011,32(1):16-18.

ZOU Ji-wu, SUN Da-jun, Lü Yun-fei, et al. Experimental research on an ocean vector noise field [J]. Journal of Harbin Engineering University, 2011, 32(1): 16-18.

[5]尚華，黃益旺，張靖. 矢量水聽器的海洋環境噪聲場空間相關[J].艦船科學與術,2009,31(10):43-46.

SHANG Hua, HUANG Yi, ZHANG Jing. Spatial correlation of anbient noise based on acoustic vector hydrophone [J]. Ship Science and Technology, 2009,31(10):43-46.

[6]張怡，席博，黃印,等.能量和協方差檢驗的聯合頻譜感知算法研究[J].航空計算技術,2011,41(2): 113-117.

ZHAIVG Yi，XI Bo，Huang YIN,et al.Collaborative detection algorithm based on energy and covariance matrix theory[J].Aeronautical Computing Technique,2011,41(2):113-117.

[7]鄒衛霞，丁奇，周正.基于特征值極限分布的雙門限頻譜感知算法[J].系統工程與電子技術,2012, 34(3): 588-591.

ZOU Wei-xia，DINU Qi，ZHOU Zheng.Double threshold spectrum sensing algorithm based on limiting eigenvalue distribution[J].2012,34(3):588-591.

[8]Penna F, Garello R, Spirito M A. Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in wishart matrices [J]. IEEE Communications Letters,2009, 13(7):507-509.

[9]Tulino A M, Verdu S.Random matrix theory and wireless communication[M]. Hanover,USA:Now Publisher Inc, 2004:3-73.

[10]Tracy C A, Widom H.On orthogonal and sympletic matrix ensembles[J].Communications in Mathematical Physics, 1996, 177(3):727-754.

[11]曹開田，楊震.基于隨機矩陣理論的DET合作頻譜感知算法[J].電子與信息學報，2010,32(1):129-134.

CAO Kai-tian, YANG Zhen. DET cooperative spectrum sensing algorithm based on random matrix theory[J]. Journal of Electronics & Information Tecnology, 2010, 32(1):129-134.