主軸-刀柄與刀柄-刀具結合面參數辨識研究

王二化，吳 波，胡友民，王 軍，楊叔子

(1. 常州信息職業技術學院 機電工程學院，江蘇 常州 213164；2. 華中科技大學 數字制造裝備與技術國家重點實驗室，武漢 430074)

顫振為金屬切削過程中較易出現的自激振動，不僅限制機床生產率，且會嚴重影響工件表面質量，加劇刀具磨損，惡化工作環境。為避免顫振發生，通常用穩定性Lobe圖輔助工藝選擇合適的切削參數，而獲取穩定性Lobe圖需先獲得刀尖頻響函數。該函數可由激振實驗方法獲得[1-2]，但對大量主軸、刀柄、刀具組合而言，實驗方法在生產實際中較難實現。為此，Schmitz等[3-4]提出動柔度耦合子結構分析方法(RCSA)。

需要強調的是，主軸-刀柄、刀柄-刀具結合面參數的準確辨識為RCSA方法的主要難點之一。目前各子結構間結合面參數辨識方法研究[5-8]尚未成熟，因此，本文在文獻[9-10]基礎上，針對結合面參數辨識問題，以傳遞矩陣法、RCSA耦合技術、PSO優化算法為基礎，提出主軸-刀柄、刀柄-刀具結合面參數辨識方法。比較預測、實驗刀尖頻響函數發現一致性較好，表明本文所提辨識方法能有效識別主軸-刀柄、刀柄-刀具結合面參數。

1 主軸-刀柄、刀柄-刀具結合面參數辨識模型

以華中數控股份有限公司自主研發的XHK立式加工中心為研究對象，基于傳遞矩陣法及RCSA耦合算法，預測加工中心刀尖頻響函數，并將刀尖頻響函數預測值與實驗值比較分析，建立主軸-刀柄、刀柄-刀具結合面參數辨識模型。

1.1 主軸裝配體、刀柄、刀具端點頻響函數

將XHK立式加工中心分解成主軸裝配體、刀柄、刀具三個子結構，見圖1。

圖1 主軸裝配體、刀柄、刀具子結構

在三個子結構中，因主軸裝配體結構復雜，較難建立精確動力學模型，故利用錘擊方法測試其端點頻響函數，實驗原理見圖2。

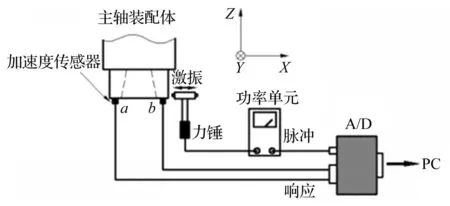
圖2 主軸裝配體端點頻響函數測試方案

(1)

(2)

(3)

據刀柄、刀具結構特點適當簡化，利用多段Timoshenko梁建立傳遞矩陣模型，見圖3。

圖3 刀柄、刀具子結構

通過傳遞矩陣法[12-13]，可得刀柄、刀具子結構端點頻響函數矩陣為

(4)

(5)

1.2 主軸、刀柄、刀具耦合模型

圖4 刀柄、刀具彈性耦合圖

具體耦合過程為

式中：

(7)

耦合后端點頻響函數矩陣為

(8)

得加工中心刀尖頻響函數矩陣及矩陣中第一個元素為

(9)

式中：

(10)

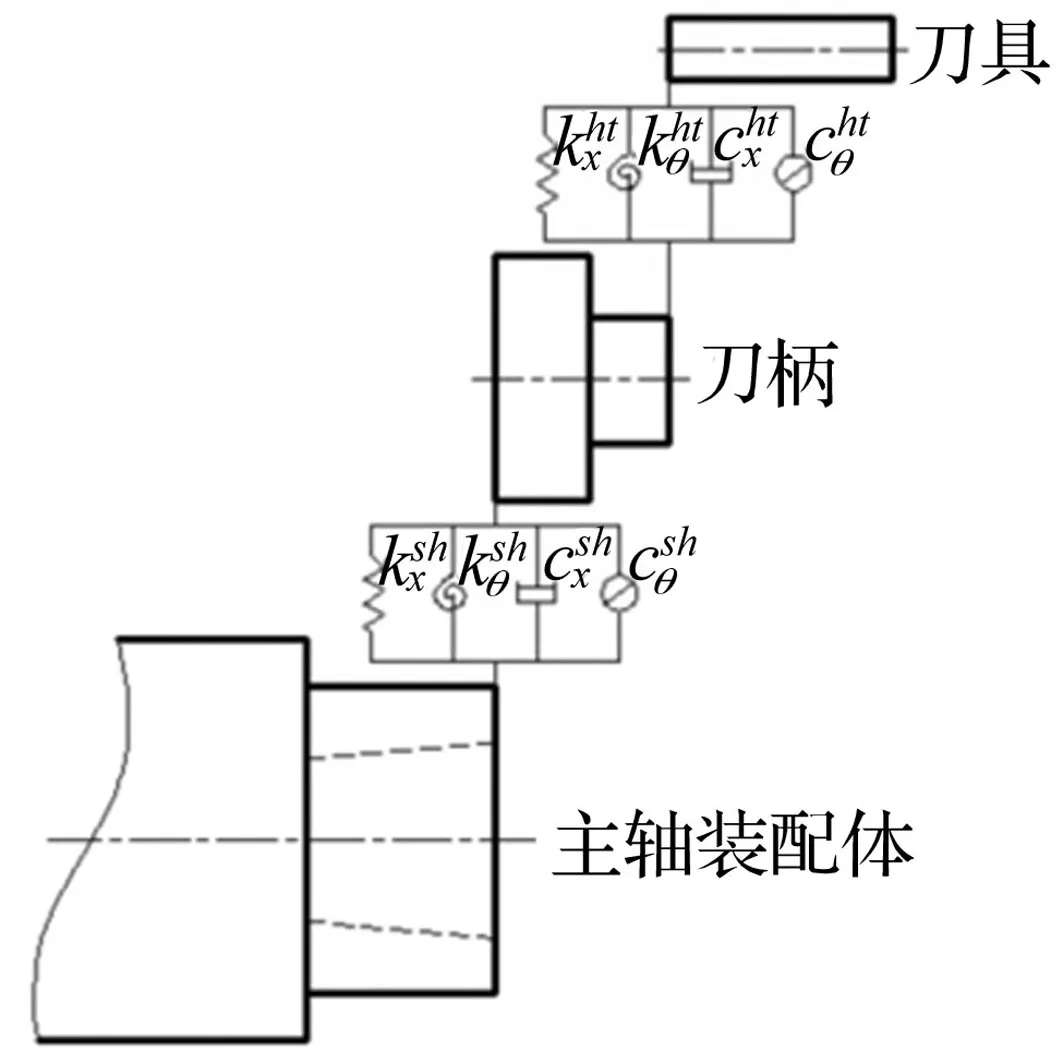
圖5 子結構彈性耦合圖

E=Ge(ω)-Gm(ω)

(11)

式中：E為參數向量α的非線性函數。總方差J(α)為

J(α)=ETE={Ge(ω)-Gm(ω)}T×

{Ge(ω)-Gm(ω)}

(12)

由于需辨識的參數較多，求解困難，故利用優化算法辨識結合面參數較合適。以總方差J(α)為目標函數，以參數向量α為優化參數，完成主軸-刀柄、刀柄-刀具結合面參數辨識。常用優化方法有牛頓法、遺傳算法、蟻群算法、退火算法及粒子群算法等。由于粒子群算法原理簡單，易實現，較適合用于連續優化問題求解，但該算法較易陷入局部最優問題，因此，為提高主軸-刀柄、刀柄-刀具結合面參數辨識精度，本文采用融合粒子群與局部搜索算法的優化算法[14]實現主軸-刀柄、刀柄-刀具結合面參數辨識。

2 主軸-刀柄、刀柄-刀具結合面參數辨識算法

粒子群優化算法由Kennedy等[15]提出，亦為群體迭代算法，但無遺傳算法中交叉、變異，無需編碼、解碼[16]，且需調整的參數不多。為處理優化問題的較好算法，并廣泛應用于諸多領域。粒子群算法具有較強的全局搜索能力。然而，該算法在迭代的最后階段易陷入局部最優。為解決PSO算法局部最優問題，吳亮等[14]提出融合粒子群與局部鄰域搜索算法的優化算法，該算法可有效克服局部最優缺陷，且計算精度、速度均具有優異性能。因此，本文選擇此算法進行主軸-刀柄、刀柄-刀具結合面參數辨識。

粒子群算法即一群粒子(鳥或蜜蜂等)在一定空間中尋找食物的模型。尋找食物時，每個粒子均由其前一個位置以一定速度向最好位置移動。影響粒子移動速度的因素包括突進、認知及社會三部分。引入慣性因子PSO模型中，每個粒子的新速度、位置算式[17]為

(13)

式中：c1，c2為兩加速度系數；w為控制粒子群全局搜索及局部搜索能力的慣性因子；r1，r2為[0,1]間任意兩個數；Vi為粒子速度；Pg為全局最好位置；αi為第i個粒子當前最好位置。

局部搜索算法針對平面局部密集結點算法，其利用確定的圓形搜索域在優化空間中進行密集點搜索[14]。局部搜索算法步驟如下。

2.1 搜索半徑確定

搜索半徑應小于或等于節點平均距離，假設節點橫坐標集為{x0，x1，x2，…，xn-1}，縱坐標集為{y0，y1，y2，…，yn-1}，節點橫、縱向平均距離分別為

(14)

式中：xmax，xmin為橫坐標極大、極小值；ymax，ymin為縱坐標極大、極小值；n為節點數目。

以任一節點(xi，yi)為圓心、搜索半徑為半徑畫圓，若無其它節點落入該搜索圓域內，則認為此節點為孤立節點；若節點(xj，yj)落入該圓域內，則以節點(xj，yj)為圓心畫圓，進行下一輪搜索，直至出現孤立節點。

2.2 搜索

將局部搜索算法引入粒子群算法后，可較好規避粒子群算法局部搜索不足問題，從而大大提高計算精度、速度。具體步驟為

(1) 初始化粒子群、局部搜索算法參數、及迭代最大次數；

(2) 如果達到最大迭代次數，程序結束，否則，轉步驟(3)；

(3) 如果當前解能滿足已設定的誤差條件，程序結束；如果達到局部搜索的啟動值，啟動局部搜索算法，查看禁忌表是否已滿，未滿，將此鄰域存入禁忌表，已滿，提高局部搜索算法啟動精度，并清空禁忌表，轉步驟(4)；若未搜索到滿足誤差條件的解，又未達到局部搜索算法啟動值，則轉步驟(2)；

(4) 在任一已啟動的鄰域內，若當前解滿足誤差條件，程序結束；若優于當前解，將當前解置換為更優解，若既未滿足誤差條件，又不優于當前解，則增大衍生解數目及鄰域范圍。

3 案例分析及實驗研究

以XHK立式加工中心為對象，進行主軸-刀柄、刀柄-刀具結合面參數辨識研究。刀柄、刀具材料密度7.8E3 kg/m3，楊氏模量E=200 GPa，尺寸見圖6。

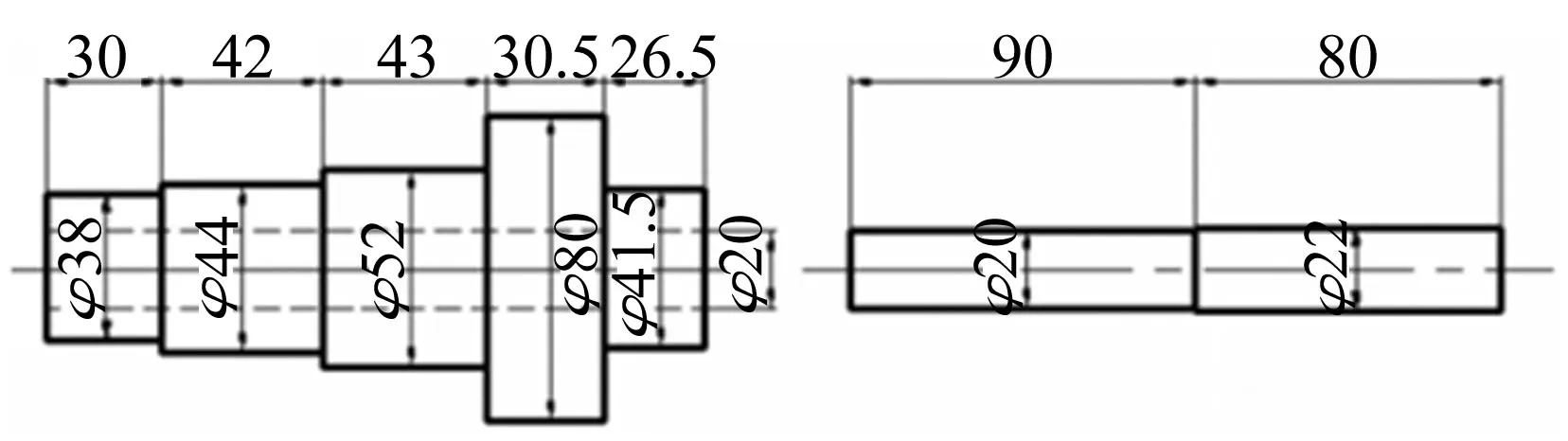
圖6 刀柄、刀具尺寸

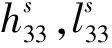
圖7 實驗裝置

圖8 主軸裝配體直接端點頻響函數hs33

獲得各子結構端點頻響函數后，利用直線、轉動彈簧阻尼單元通過RCSA方法耦合三子結構，進行刀尖頻響函數預測。其中，主軸-刀柄、刀柄-刀具結合面參數需辨識未知量。為識別主軸-刀柄、刀柄-刀具結合面參數，通過激振實驗方法獲取測試的XHK加工中心刀尖頻響函數(圖7(b))，將加速度傳感器固定在刀具底端，利用力錘敲擊刀尖位置獲取激振力及加速度信號，將采集的信號傳輸到LMS數據采集系統，采用譜分析技術獲取刀尖位置直接、交叉頻響函數。在相同條件下，連續測試5次取平均值。

利用RCSA方法，通過直線及轉動彈簧阻尼單元耦合主軸裝配體、刀柄、刀具三個子結構，獲得預測刀尖頻響函數。考慮辨識算法中有大量矩陣運算，用MATLAB軟件編程，實現主軸-刀柄、刀柄-刀具結合面參數辨識。計算時間取決于方程數量、頻域范圍及單位頻率內的頻率點數。用計算機(Pentium?Dual-Core CPU 2.93 GHz, 2.0 GB RAM)計算，完成主軸-刀柄、刀柄-刀具結合面參數辨識，耗時31 min，計算結果見表1。

表1 結合面參數辨識結果

為驗證本文所提參數辨識算法的正確性，將辨識出的各結合面參數代入刀尖頻響函數預測模型，將所得預測的刀尖頻響函數與測試的刀尖頻響函數對比見圖10。由圖10看出，除在頻率1 200 Hz峰值附近有波動外，預測、測試的刀尖頻響函數一致性較好。預測結果表明，本文方法能有效辨識主軸-刀柄、刀柄-刀具結合面參數。

為驗證辨識算法的普適性，改變刀具懸臂長度分別為90 cm、100 cm、110 cm，并稱為案例2，3，4。利用本文方法辨識不同懸臂長度的主軸-刀柄、刀柄-刀具結合面參數，并將預測與測試刀尖頻響函數進行比較。為量化預測和測試刀尖頻響函數的一致性，基于誤差向量E，構造預測刀尖頻響函數平均誤差表達式為

(15)

式中：m為頻率測試點數；Ei為誤差向量E的第i個元素。

四組案例平均誤差結果見表2。由表2看出，不同刀具懸臂長度，預測、測試的刀尖頻響函數一致性均較好。由此可論證本文辨識算法的普適性。此辨識算法可有效辨識與本對象具有相似結構的主軸-刀柄、刀柄-刀具結合面參數。

表2 四組案例預測、測試結果平均誤差

4 結 論

(1) 基于傳遞矩陣、RCSA耦合方法及PSO優化算法，提出主軸-刀柄、刀柄-刀具結合面參數辨識方法，通過Timoshenko梁理論結合傳遞矩陣方法，計算刀柄、刀具端點頻響函數，利用錘擊實驗方法測試主軸裝配體端點頻響函數。

(2) 用RCSA方法耦合三子結構，并計算加工中心刀尖頻響函數；以減小預測與分析刀尖頻響函數間誤差為目標，利用改進的PSO方法辨識主軸-刀柄、刀柄-刀具結合面參數；比較預測與實驗刀尖頻響函數表明，本文所提方法能有效辨識主軸-刀柄、刀柄-刀具結合面參數，并具有較高的普適性，可用于相似結構的結合面參數辨識。

[1]Budak E,Altintas Y. Analytical prediction of chatter stability in milling-part i: general formulation; part ii: application to common milling systems[J]. Transactions of ASME, Journal of Dynamic Systems, Measurement,and Control,1998,120(1):22-36.

[2]Kivanc E B, Budak E. Structural modeling of end mills for form error and stability analysis[J]. International Journal of Machine Tools and Manufacture,2004,44(11):1151-1161.

[3]Schmitz T. Predicting high-speed machining dynamics by substructure analysis[J]. CIRP Ann.,2000,49(1):303-308.

[4]Schmitz T, Davies M, Kennedy M. Tool point frequency response prediction for high-speed machining by RCSA[J]. Journal of Manufacturing Science and Engineering, 2001,123(4):700-707.

[5]Schmitz T L,Powell K, Won D,et al.Shrink fit tool holder connection stiffness/damping modeling forfrequency response prediction in milling[J]. International Journal of Machine Tools & Manufacture, 2007, 47(9):1368-1380.

[6]Movahhedy M R,Gerami J M.Prediction of spindle dynamics in milling by sub-structure coupling[J]. International Journal of Machine Tools & Manufacture, 2006, 46(3/4):243-251.

[7]Namazi M, Altintas Y, Abe T, et al.Modeling and identification of tool holder-spindle interface dynamics[J]. International Journal of Machine Tools & Manufacture, 2007, 47(9):1333-1341.

[8]?zsahin O, Ertürk A, ?zgüven H N,et al.A closed-form approach for identification of dynamical contact parameters in spindle-holder-tool assemblies[J]. International Journal of Machine Tools & Manufacture, 2009, 49(1):25-35.

[9]胡峰,吳波,胡友民,等. 基于概率神經網絡和KS檢驗的機械狀態監測[J].振動與沖擊，2008, 27(4):56-62.

HU Feng, Wu Bo,HU You-min,et al. Machine condition monitoring based on probabilistic neural network and KS inspection[J]. Vibration and Shock, 2008, 27(4):56-62.

[10]胡峰,吳波,胡友民,等. 利用粒子群優化算法實現阻尼和頻率的精確識別[J].振動與沖擊,2009,28(7):8-11.

HU Feng, Wu Bo,HU You-min,et al. Precise identification of damping and frequency by using particle swarm optimization[J]. Vibration and Shock, 2009, 28(7):8-11.

[11]Schmitz T, Duncan G S.Three-component receptance coupling substructure analysisfor tool point dynamics prediction[J]. Journal of Manufacturing Science and Engineering, 2005, 127(4):781-790.

[12]包世華. [M].武漢:武漢理工大學出版社, 2005.

[13]楊肅,唐恒齡,廖伯瑜,等. 機床動力學(Ⅱ)[M]. 北京：機械工業出版社,1983.

[14]Wu Liang,Jiang Yu-ming.Optimization algorithm integrates PSO with local neighborhood search[J]. Computer Engineering and Design, 2010,31(7):

[15]Kennedy J, Eberhart R C.Particle swarm optimization[C]. In: Proceedings of IEEE International Conference in Neural Networks, 1995:1942-1948.

[16]Chen T Y, Chi T M.On the improvements of the particle swarm optimization algorithm[J]. Advances in Engineering Software,2010,41(2): 229-239.

[17]Eberhart R C, Shi Y. A modified particle swarm optimizer[C]. In: Proceedings of 1998 IEEE World Congress on Computational Intelligence, 1998:69-73.