基于HHT的數控機床主軸振動監測系統的研制
萬海波, 楊世錫
(1. 浙江水利水電專科學校 機械電子工程系,杭州 310018; 2. 浙江大學 機械工程學系,杭州 310027)
數控機床主軸運轉正常與否直接影響機床的加工質量與生產效率。主軸振動信號包含大量反映其工況特征信息[1-2],進行主軸振動實時監測、對保障機床加工質量及生產效率具有重要意義。近年來,對數控機床主軸振動監測方法已進行廣泛研究,并開發出相應監測系統。Chang等[3]在分析振動信號頻譜特征基礎上,開發出基于頻譜分析的數控機床主軸振動監測系統。Wang等[4]通過基于級聯雙穩隨機共振系統微弱特征提取方法對機床主軸信號進行分析,并開發出狀態監測系統。高榮等[5]將小波方法用于主軸振動監測,開發出抗干擾能力較強的主軸振動監測系統。周玉清等[6]研究負載、位置及瞬時加速度等條件對實測信號影響,提出能追溯故障源頭的機床狀態監測系統。袁冬梅等[7]用基于Labview 的虛擬儀器技術,開發出數控機床主軸軸承振動監測系統。
當數控機床主軸工況條件變化或故障發生時,其振動信號具有明顯非平穩特性。因此,主軸振動信號中非平穩性較強的局部特征可表征其工況變化及某些故障存在[8]。文獻[3-4,6-7]研制的監測系統均采用基于平穩過程的經典信號處理方法,無法同時兼顧信號在時、頻域的全貌及局部特征。文獻[5, 9]雖利用小波變換進行機床主軸振動信號時頻特征分析,但小波變換本質為窗口可調的傅里葉變換,一旦信號局部特征尺度小于所選基小波的特征尺度,對數控機床主軸振動信號中因工況變化或故障發生所致非平穩性較強的局部特征很難獲得準確描述。Huang等[10]提出的基于經驗模式分解(Empirical Mode Decomposition, EMD)希爾伯特-黃變換(Hilbert-Huang Transform, HHT)時頻分析方法將信號由高頻至低頻分解為若干固有模式函數(Intrinsic Mode Function, IMF),再對每個IMF做希爾伯特變換(Hilbert Transform, HT),用以描述非平穩信號的時頻特征。該非平穩信號時頻特征的描述形式能準確反映信號頻率成分隨時間變化規律,因而被廣泛用于非平穩數據分析[11]。在機械狀態監測與故障診斷領域基于EMD、HHT的相關研究,已取得有益成果[11-14]。
由于HHT過程中EMD算法對數據采用批處理方式,無法對實時數據進行分析。Rilling等[15]提出在線EMD方法,實現對實時數據分析。本文結合HHT方法分析非平穩數據優勢,在在線EMD方法基礎上,提出基于HHT的數控機床主軸振動信號特征提取方法,并應用于研制的數控機床主軸振動監測系統,對主軸振動信號時頻特征進行在線監測。
1 數控機床主軸振動監測系統總體設計
本文結合數控機床主軸振動信號特點,在研究大量旋轉機械狀態監測系統基礎上設計出數控機床主軸振動監測系統,結構框圖見圖1。數控機床工作過程中,主軸振動加速度信號通過數據采集模塊,傳輸至上位機。上位機軟件系統包括時域波形監測及特征數據監測兩模塊,其中特征數據監測模塊具有監測頻域特征量及時頻特征量功能。選取振動信號功率譜密度作為機床主軸振動響應的頻域特征量。選取基于HHT的時頻分布作為被監測時頻特征量,該特征量同時描述機床主軸振動響應的時、頻域信息,能有效反映特征頻率隨時間變化規律。
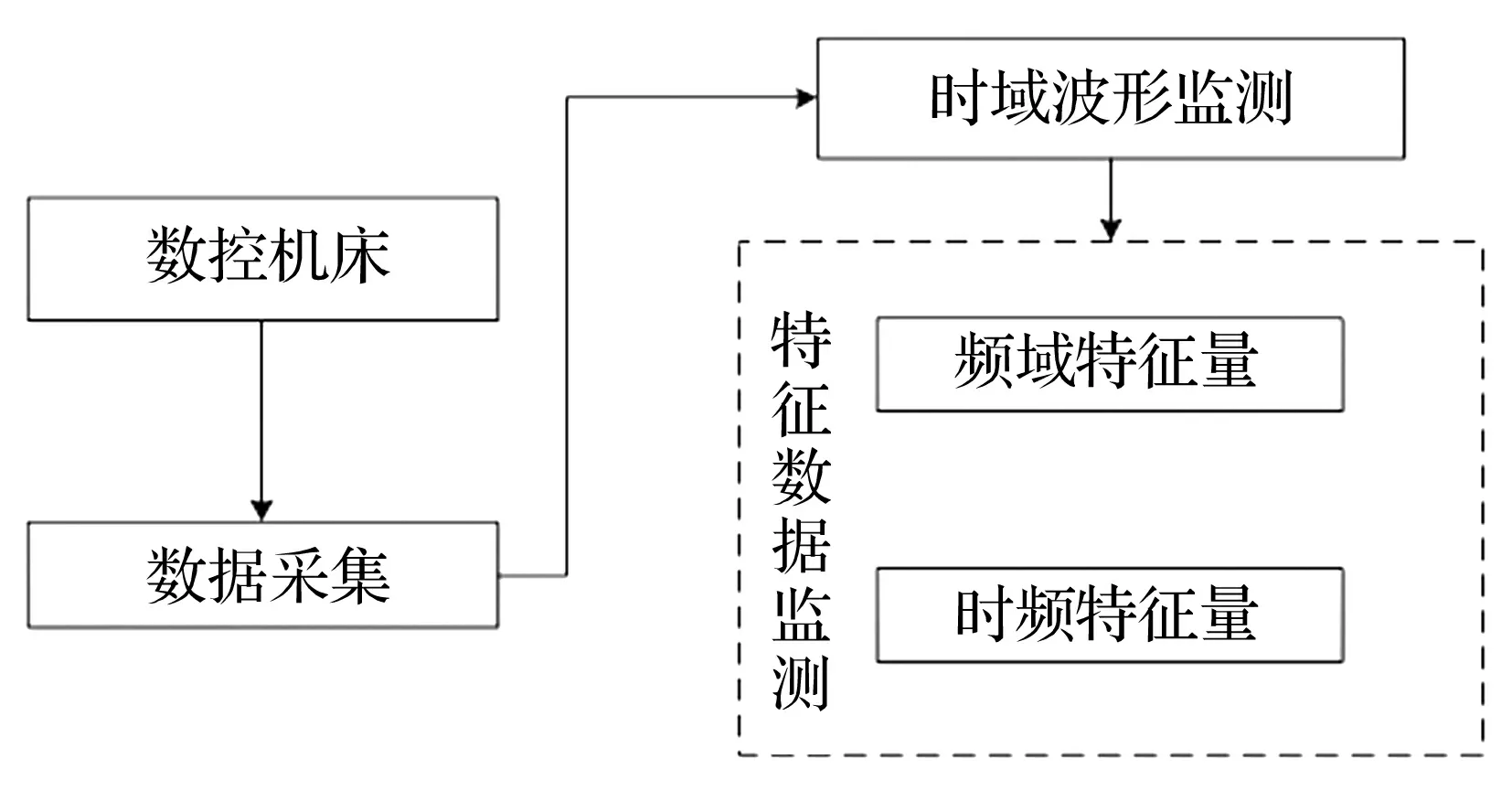
圖1 數控機床主軸振動監測系統結構框圖
2 監測系統硬件研制
系統硬件采集數據的實時性、精確性及數據傳輸的快速性是實現數控機床主軸振動監測的首要前提。基于上述要求,本文將數控機床主軸監測系統硬件部分分為傳感器、信號調理模塊、數據采集模塊及數據通訊模塊。系統硬件結構框圖見圖2。其中,傳感器將主軸振動位移與轉速轉變成電信號,信號調理模塊將傳感器電信號調理以滿足數據采集要求,數據采集模塊將電信號進行A/D轉換,數據通訊模塊將實時數據上傳至上位機。

圖2 數控機床主軸振動監測系統硬件結構框圖
信號調理模塊用自行設計開發的信號調理電路,包含振動信號、鍵相信號的調理兩部分。振動信號調理電路由輸入跟隨電路、交流隔離電路、加法電路、放大電路及低通濾波電路組成。鍵相信號由輸入調節電路、信號放大電路、光耦隔離電路及穩壓整形電路組成。數據采集模塊含主控制子模塊及A/D子模塊,主控芯片選Altera公司EPIc6Q24O的FPGA,A/D選Maxim公司的Max125A/D轉換芯片。數據通訊模塊用PC 104總線通訊方式。數控機床主軸振動監測硬件系統實物見圖3。

圖3 數控機床主軸振動監測硬件系統實物圖
3 監測系統軟件設計
數控機床主軸振動監測系統一般采用基于平穩過程的經典信號處理方法,難準確描述因工況變化或故障發生所致非平穩性較強的局部特征。因此,數控機床主軸振動監測系統不僅需能監測振動信號時域波形及頻域特征量,且更需監測能反映振動信號局部特征的時頻特征量。
3.1 時頻特征量提取方法
針對數控機床主軸振動信號的非平穩特性,本文采用HHT方法提取時頻特征量。HHT方法為基于經驗模式分解(Empirical Mode Decomposition, EMD)的非平穩信號分析方法,即將頻域信號由高頻至低頻分解為若干IMF頻率分量,再對每個IMF分量做希爾伯特變換(Hilbert Transform, HT),從而描述非平穩信號時頻特征。HHT包括EMD與HT兩步。對信號x(t)進行EMD分解,算法基本思路為:①通過三次樣條曲線分別對x(t)所有極大值點、極小值點進行插值,獲得x(t)的上、下包絡線;②計算上、下包絡均值m(t);③去除信號中均值m(t),提取信號細節成分d(t)=x(t)-m(t),并利用其提取第一階IMF;④將第一階IMF從x(t)中去除,余量作為新信號重復執行步驟①~③,陸續提取各階IMF。提取時,需對步驟③中d(t)篩分運算。當d(t)同時滿足IMF定義及迭代終止條件時篩分運算終止。經EMD分解后,x(t)可表示為各階IMF與趨勢項之和:
(1)
其中:K為IMF分量數;dk(t)(k=1~(K-1))為第k階IMF分量,并記為第K階IMF。
對各階IMF分別做希爾伯特變換:
(2)
式中:PV為柯西主分量。將dk(t),Dk(t)組成第k階IMF解析形式為:
Zk(t)=ak(t)exp[iθk(t)]
(3)
其中:
(4)
(5)
式中:ak(t)為信號幅值;θk(t)為信號相位。
信號瞬時頻率定義為θk(t)的導數:
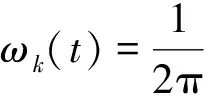
(6)
原信號x(t)表示為:
(7)
作為時間t的函數,由式(7)的信號x(t),幅值ak(t)及瞬時頻率ωk(t)可準確描述非線性、非平穩信號每個時刻所含頻率成分。
3.2 監測系統軟件實現
基于HHT的數控機床主軸振動監測系統軟件包括時域波形監測、特征數據監測兩模塊。時域波形監測模塊中主要監測振動信號的時域特征。特征數據監測模塊包含頻域征量監測與時頻特征量監測兩個功能。監測系統軟件用Microsoft Visual Studio 2008開發應用客戶端,用MS SQL Server2005 開發后臺支持數據庫,用MATLAB R2009b編寫算法程序。監測系統中時頻特征量提取部分程序代碼為:
private void time_frequency_analysis_FormClosed(object sender, FormClosedEventArgs e)
{int num = 0;
for (int i = 0; i < Main.win_number; i++)
{if (this.Text == Main.win_name[i].Text)
{num = i;}}
for (int i = num; i < Main.win_number; i++)
{Main.win_name[i]= Main.win_name[i + 1];}
Main.win_number--;
timer1.Enabled = false;}
private void time_frequency_analysis_Load(object sender, EventArgs e)
{string sqlstr = null;
sqlstr = "select Channel1 from spindle";
ds = Db.SqlExe_DS(sqlstr);
for (int i = 0; i < ds.Tables[0].Rows.Count; i++)
{x[i]= Convert.ToDouble(ds.Tables[0].Rows[i][0]); }
timer1.Enabled = true;}
4 監測系統測試
為驗證數控機床主軸振動監測系統的有效性,利用該系統對TAKUMI立式加工中心主軸振動進行監測。測試中,系統采樣頻率1280 Hz,原始數據監測模塊顯示的時域波形時長設為0.2 s。將數控機床主軸轉速調至3840 r/min,待主軸穩定運行一段時間后,用銅棒接觸主軸使轉速發生波動。系統監測到無銅棒接觸時主軸振動信號時域波形,見圖4。銅棒接觸時系統監測到的主軸振動信號時域波形見圖5。比較圖4、圖5,由時域波形較難看出兩者差別。

圖4 無銅棒接觸數控機床主軸振動時域波形圖
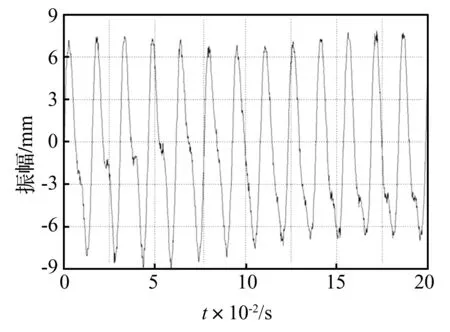
圖5 銅棒接觸時數控機床主軸振動時域波形圖
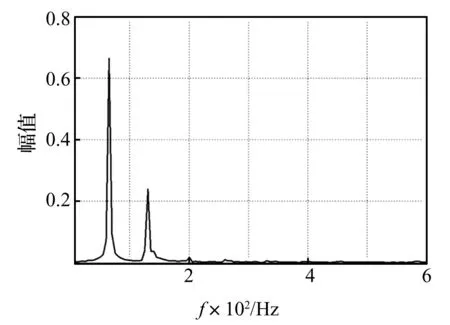
圖6 系統監測的頻域分布圖

圖7 系統監測時頻分布圖
功率譜密度反映能信號頻率成分在一定時間間隔內的平均能量分布特征,可作為被監測頻域特征量分析。系統監測的平穩特征量(功率譜)見圖6,其轉頻(64 Hz)特征量與倍頻 (128 Hz)特征量較明顯,高次倍頻特征量較小。但由監測到的平穩特征量中無法判斷轉子系統外部激勵(銅棒接觸)的發生時間與持續時長。
HHT方法所得時頻分布能反映特征頻率隨時間變化規律。振動信號HHT時頻分布見圖7。由圖7看出,時頻分布中倍頻特征成分在無銅棒接觸的時間間隔內較明顯,在銅棒接觸時間間隔(圖中0.4~1.2 s,4~5 s)內消失,且時頻能量分布中倍頻特征成分的消失、重現時間點與外部激勵發生、終止時間點吻合。由亞諧波共振理論知[15],主軸轉頻接近主軸系統徑向一階固有頻率的1/2時,會激發出轉頻的二倍頻成分;在0~0.4 s時間間隔內存在明顯轉頻(64 Hz)及二倍頻(128 Hz)成分。由此推測,機床主軸因不對中發生亞諧波共振。在0.4~1.2 s時間間隔內,因銅棒與主軸的摩擦作用,使機床轉速發生微量波動,進而使轉頻二倍頻遠離主軸系統徑向一階固有頻率,亞諧波共振現象消失。1.2~4 s時間間隔內,因銅棒離開主軸,主軸轉頻又重新穩定在1/2徑向一階固有頻率,亞諧波共振現象重現。同理可說明4~5 s間隔內銅棒碰摩主軸時振動信號頻率構成。因此,基于HHT的數控機床主軸振動監測系統時頻特征監測子模塊,不僅能描述數控機床主軸振動信號頻域信息,亦能跟蹤頻率成分隨時間變化,可為分析數控機床主軸振動信號產生非平穩性原因提供依據。
5 結 論
(1)本文闡述的基于HHT的數控機床主軸振動監測系統設計、實現,采用主控模塊與基于PC104總線結合采集方式,可保證數據采集的實時性及數據傳輸的準確性。
(2)采用在線EMD方法,獲得主軸振動信號基于HHT的時頻特征量,實現對主軸振動信號時頻特征量的實時監測。現場測試表明,該系統不僅能準確監測數控機床主軸振動信號頻域特征量,且可實現對時頻特征量的實時監測,使系統能更直觀、全面反映數控機床主軸的工作狀況。
參 考 文 獻
[1]周大帥. 高速電主軸綜合性能測試及若干關鍵技術研究[D]. 北京:北京工業大學,2011.
[2]董新峰,李郝林,余慧杰.基于最大熵原理與鑒別信息的機床主軸系統退化分析[J]. 振動與沖擊,2013,32(5):62-64.
DONG Xin-feng, LI Hao-lin, YU Hui-jie. Degradation analysis of machine tool spindle based on maximum entropy and discrimination information[J]. Journal of Vibration and Shock,2013,32(5):62-64.
[3]Chang C F, Chen J J. Vibration monitoring of motorized spindles using spectral analysis techniques[J]. Mechatronics, 2009,19(5):726-734.
[4]Wang T Y, Li H W. Research on intelligent CNC platform based on hierarchical and distributed architecture for grinding machine [J]. Key Engineering Materials, 2004, 259-260: 715-719.
[5]高 榮,葉佩青,蔣克榮,等. 基于小波奇異性的電主軸振動信號處理[J].吉林大學學報(工學版),2010,40(4):1025- 1028.
GAO Rong,YE Pei-qing,JIANG Ke-rong,et al.Vibration signal processing of motor spindle based on wavelet singularity[J].Journal of Jilin University (Engineering and Technology Edition),2010, 40(4):1025-1028.
[6]周玉清,梅雪松,姜歌東,等. 基于內置傳感器的大型數控機床狀態監測技術[J].機械工程學報,2009,45(4):125-130.
ZHOU Yu-qing,MEI Xue-song,JIANG Ge-dong,et al. Technology on large scale numerical control machine tool condition monitoring based on built-in sensors[J]. Journal of Mechanical Engineering, 2009,45(4):125-130.
[7]袁冬梅,羅 輯,唐毅峰. 數控機床振動監測系統設計[J]. 機床與液壓, 2007, 35(4): 221-222, 250.
YUAN Dong-mei, LUO Ji, TANG Yi-feng.Design on vibration monitor system of NC machine[J]. Machine Tool & Hydraulics, 2007,35(4):221-222,250.
[8]何正嘉,訾艷陽,孟慶豐,等. 機械設備非平穩信號的故障診斷原理及應用[M]. 北京:高等教育出版社,2001.
[9]Liao T W, Ting C F, Qu J, et al. A wavelet-based methodology for grinding wheel condition monitoring [J]. International Journal of Advanced Manufacturing Technology, 2007, 47: 580-592.
[10]Huang N E, Shen Z, Steven R L, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis [C]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. United Kingdom: The Royal Society, 1998, 454(1971): 903-995.
[11]何正嘉,陳 進,王太勇,等. 機械故障診斷理論及應用[M]. 北京:高等教育出版社,2010.
[12]Xiong X, Yang S X, Gan C B. A new procedure for extracting fault feature of multifrequency signal from rotating machinery[J]. Mechanical Systems ans Signal Processing, 2012, 32: 306-319.
[13]曹沖峰,楊世錫,楊將新. 大型旋轉機械非平穩振動信號的EEMD降噪方法[J].振動與沖擊,2009,28(9): 33-38.
CAO Chong-feng,YANG Shi-xi,YANG Jiang-xin. De-noising method for non-stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition[J].Journal of Vibration and Shock, 2009, 28(9):33-38.
[14]趙 玲,劉小峰,秦樹人,等. 消除經驗模態分解中混疊現象的改進掩膜信號法[J].振動與沖擊,2010,29(9): 13-18.
ZHAO Ling,LIU Xiao-feng,QIN Shu-ren.et al.Use of masking signal to improve empirical mode decomposition [J]. Journal of Vibration and Shock,2010, 29(9): 13-18.
[15]Rilling G, Flandrin P, Goncalves P. On empirical mode decomposition and its algorithms[C]. IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03, Grado (I),2003.
[16]Tejas H, Ashish K, Experimental investigations on vibration response of misaligned rotors[J]. Mechanical Systems and Signal Processing,2009,23:2236-2252.

