考慮螺栓球節點半剛性的網格結構有限元模型修正研究
劉才瑋, 張毅剛,2, 吳金志
(1. 北京工業大學 空間結構研究中心,北京 100124;2. 北京工業大學 城市與工程安全減災省部共建教育部重點實驗室,北京 100124)
健康監測已成為保證工程結構安全使用的有效手段。對重要結構的健康監測已有諸多研究。建立合理的有限元模型對研究結構動力特性是工程結構長期健康監測、狀態評估基礎[1],而據施工圖紙建立的結構初始有限元模型含較多理想化信息或簡化假定。由于空間網格結構復雜,自由度繁多、節點連接復雜、有限元離散化等因素必將導致按初始有限元模型計算的結構響應與實際結構存在一定偏差。因此為能對結構進行準確的模擬,需用理論及方法減小此差異,即對初始有限元模型進行修正。
傳統的結構模型修正與基于模態分析的結構損傷識別方法在實際應用中均易受環境影響、模型依賴性強、系統容錯性差等,而人工神經網絡(Artificial Neural Networks,ANN)以良好的非線性映射能力、強大的解決反問題能力、實時計算及系統良好的魯棒性在在工程應用中得到普遍重視[2]。Zapico等[3]利用兩層前饋多層感知器(MLP)基于實測數據對小型鋼結構框架進行模型修正。瞿偉廉等[4]建立基于徑向基神經網絡的空間網架結構有限元模型修正計算方法,并以具有13個球節點、32根桿件的焊接球節點網架為例,進行節點固結系數識別。但以節點固結系數表示的空間有限元模型建模較困難,試驗模擬較復雜。劉暉等[5]以結構自振頻率為輸入,節點連接剛度參數為輸出訓練BP神經網絡,試圖使修正的焊接球節點網架結構有限元模型具有與實測結果一致自振頻率,且應用于深圳市民中心網架結構有限元模型修正中。但由于未考慮振型因素影響,修正精度有待提高。何浩祥等[6]基于子結構建立以頻率為輸入、彈性模量為輸出的神經網絡遞推模型修正法,并對單層球面網殼進行修正。但修正參數僅為桿件的彈性模量。考慮通常空間網格結構為鋼結構,可近似認為桿件物理參數精確,主要需修正桿件端部節點連接剛度。
由于螺栓球節點加工制作工藝簡單,現場安裝方便,避免高空焊接作業,廣泛應用于網格較規則的中、小跨度網架、雙層網殼結構中[7-8]。螺栓球節點實質為典型的半剛性節點,設計中假設節點為鉸接,即不考慮節點的抗彎剛度。此可能為動力測試結果與有限元分析結果不符的重要原因,但針對螺栓球節點的模型修正研究較少。張毅剛等[9]曾對具有157個節點、414根桿件的單層柱面網殼振動臺試驗模型的四種螺栓球節點進行精細化建模,利用摩擦系數、接觸分析模擬高強螺栓與鋼球之間的少許滑動,忽略銷及預緊力影響,獲得螺栓球連接彎矩-轉角(M-θ)曲線。并將節點連接簡化為慣性矩I與原桿件相同的節點單元,從而依據所得曲線確定節點單元彈性模量。經反復試算優選確定摩擦系數、接觸參數,獲得與Φ32×2.15、Φ48×3.5、Φ60×3.5、Φ89×3.75螺栓對應的四種節點單元
剛度折減系數分別為:0.524、0.466、0.317、0.122。由于空間網格結構節點種類繁多,過程較繁瑣,不便于工程應用。本文在文獻[9]基礎上,避開螺栓球節點精細化建模時復雜參數的取值問題,利用單層柱面網殼試驗模型實測頻率及部分測點振型分量構造輸入參數,采用廣義回歸神經網絡 (GRNN)[10]對節點單元剛度折減系數分步修正,試圖找到螺栓球節點模型修正新方法。
1 單層柱面網殼動力測試及相關性分析
單層柱面網殼振動臺試驗模型(以下簡稱試驗網殼)縱向長21.0 m,寬3.0 m,矢高0.75 m,見圖1。采用螺栓球節點,加大螺栓與套筒尺寸以增加連接處轉動剛度。桿件類型分四種,對應四種套筒、螺栓,具體見表1。螺栓球節點型號BS180。該模型縱向有7個柱距,且每個柱距間結構桿件個數及類型相同或相似,螺栓球及桿件種類以第2個柱距(即第2跨)為例,見圖2。在北京工業大學8個子振動臺構成的臺陣上進行試驗,現場見圖3。據數值模擬中試驗網殼模態結果,傳感器采用測點布置優先級綜合排序方法進行布置[11],共44個加速度傳感器,其中Y向與Z向各22個,見圖4。動力特性測試采用正弦激振法。由于結構較長,利用兩臺50 N電磁激振器、DF1010超低頻信號發生器及KD5701功率放大器,對該模型前四階自振頻率及前三階振型進行測試。
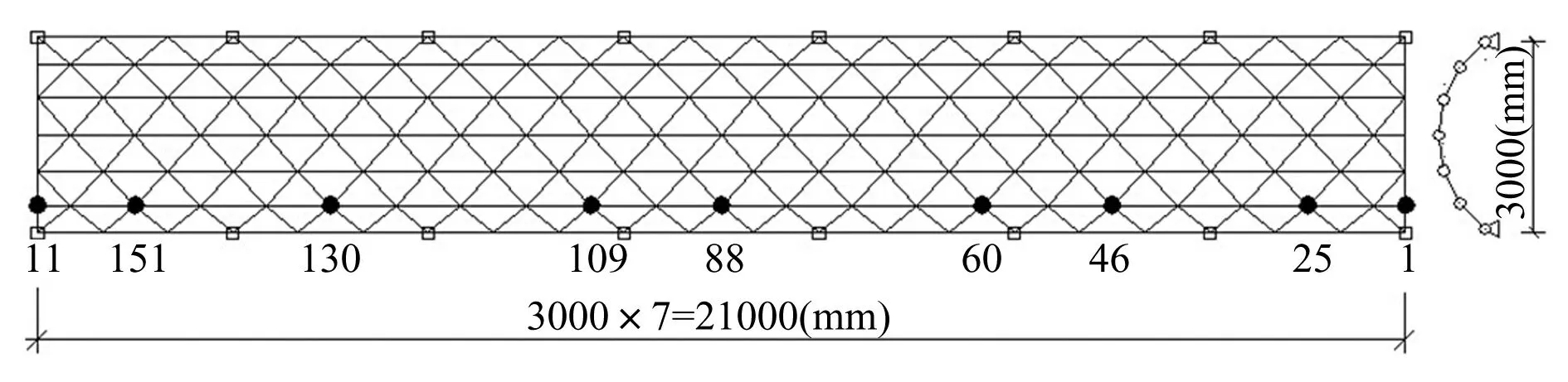
圖1 單層柱面網殼試驗模型
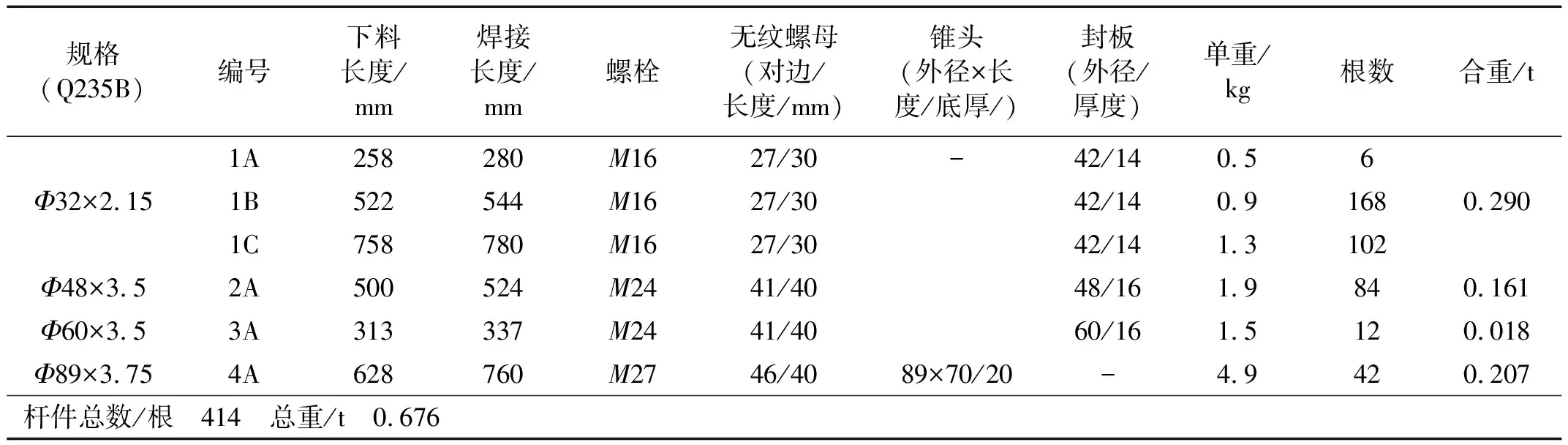
表1 桿件材料表

圖2 螺栓球及桿件種類
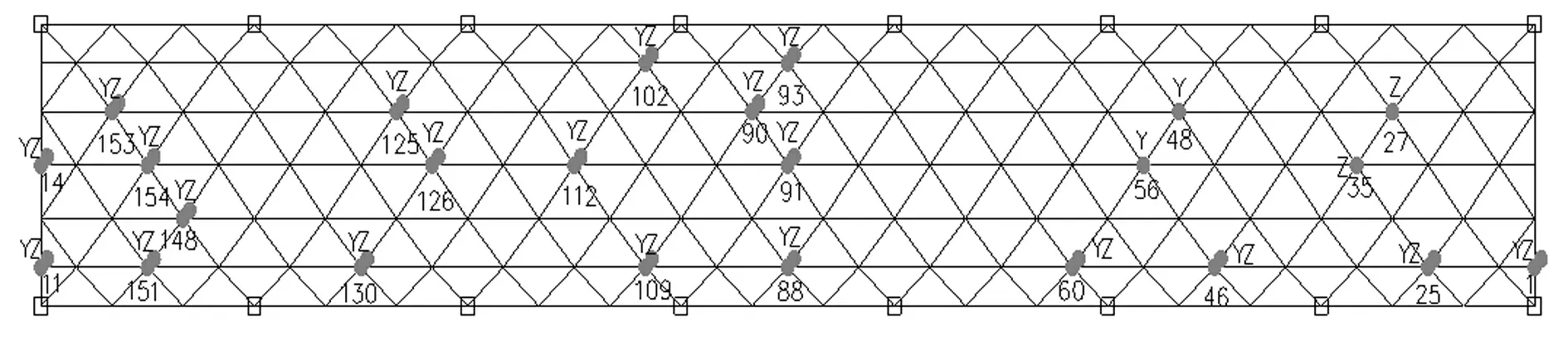
圖4 加速度傳感器布置圖
單層網殼工程設計中將球心至球心視為一根桿件,用梁單元模擬,節點視為剛接,本文稱為剛性模型。為評價剛性模型的合理性,對其模態計算結果與實測模態數據進行相關性分析。設ωti=(i=1,2,…,n)表示實際測量自振頻率;φti=(i=1,2,…,n)為實測振型;ωci=(i=1,2,…,n)為理論計算自振頻率;φci=(i=1,2,…,n)為理論計算所得振型。采用參數衡量修正后模型優劣、頻率變化率及模態置信準則分別定義為:
(1)
式(1)可度量第i階自振頻率及振型的優劣,ER(ωti,ωci)→0,MAC(φti,φci)→1說明修正結果好[12]。表2為試驗網殼的頻率實測值與剛性模型計算值對比,由表2可看出第二階誤差最小為16.58%。產生誤差原因較多,如支座剛度、桿件及節點坐標偏差等,但剛性模型未合理考慮螺栓球節點的半剛性為主要原因。因此為獲得較精確的數值模型,本文擬由螺栓球節點半剛性入手,對剛性模型進行有限元修正。
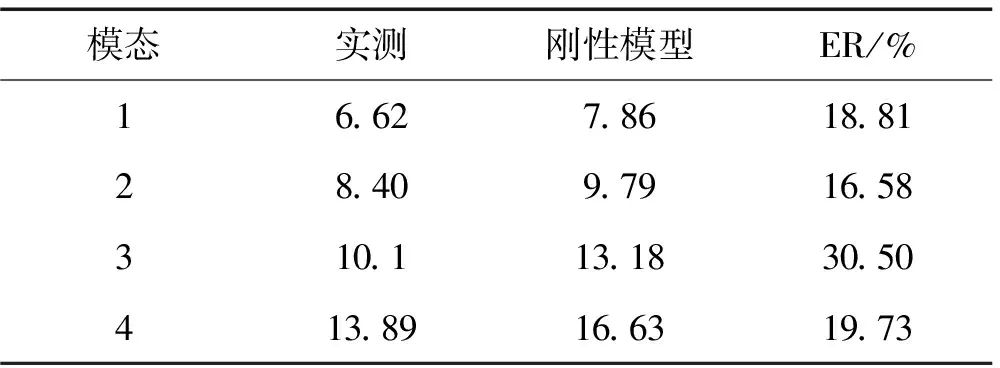
表2 頻率實測值與有限元分析值對比(Hz)
2 考慮節點半剛性的螺栓球網格結構模型修正方法
2.1 半剛性模型建立
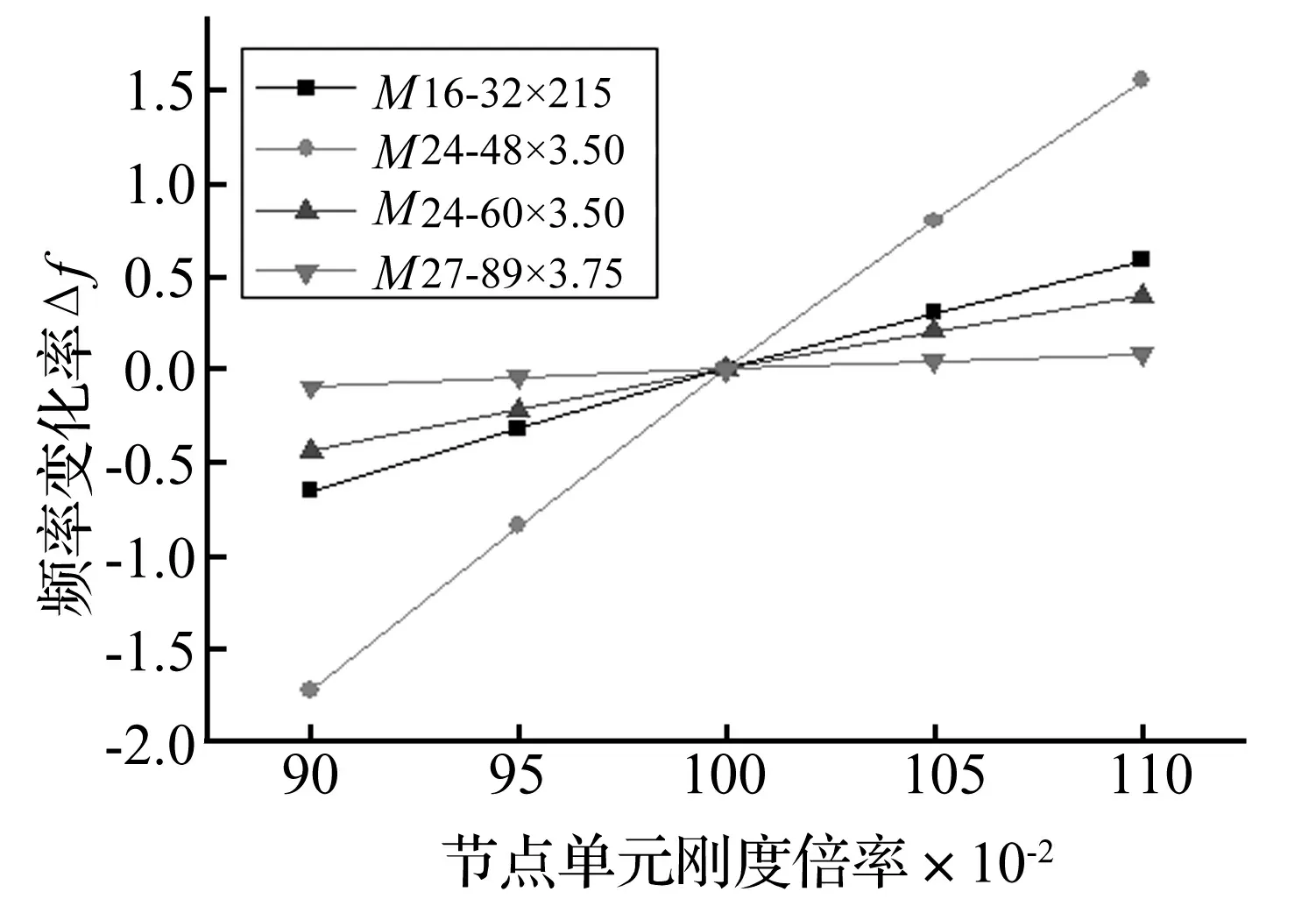
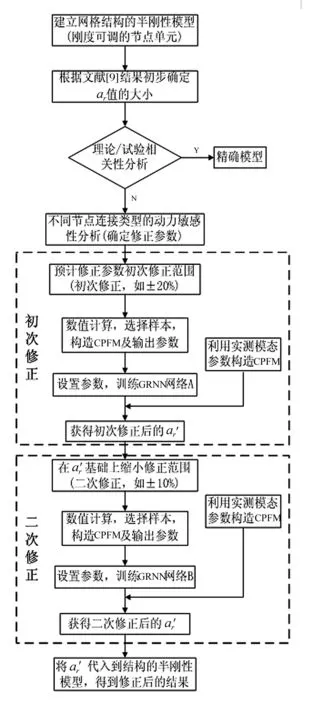
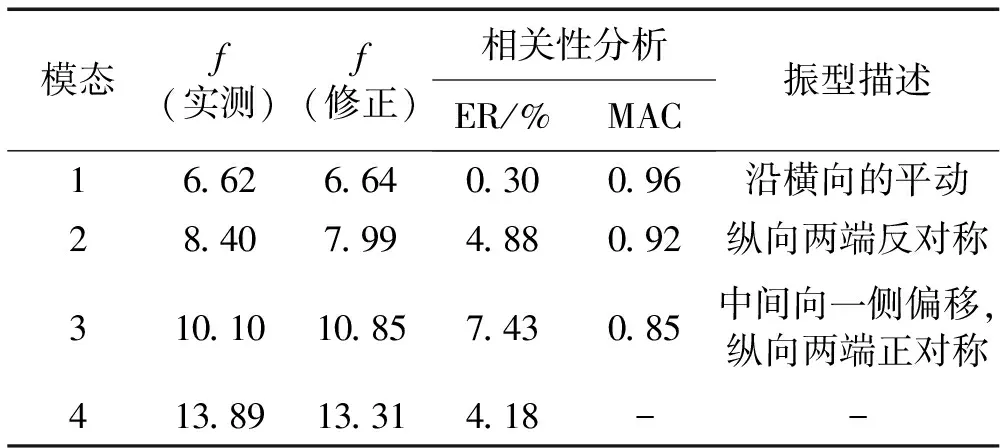
網格結構有限元模型準確關鍵取決于桿件與螺栓球節點連接方式的計算假設。本文建立剛度可調桿件單元模擬桿端節點連接,即螺栓球節點半剛性用具有剛度可調節點單元描述,稱此模型為半剛性模型,見圖5。其中L為節點單元長度;a為單元剛度折減系數(節點單元與桿件單元剛度比值),0 圖5 剛度可調節點單元 空間網格結構有限元模型中參數眾多,但每個參數對大型結構動力特性的敏感程度不同。因此在模型修正中,若考慮所有參數,不僅計算量大,計算時間長、效率低,且分析結果不易收斂。故應選反應敏感的參數作修正對象,而參數動力敏感性分析成為解決該問題的有效途徑[13]。 試驗網殼節點連接有四種類型,即:M16-32×2.15、M24-48×3.5、M24-60×3.5、M27-89×3.75。為獲得其動力敏感性,以頻率f1.0[9]考察節點單元剛度分別按0.9,0.95,1.05,1.1倍頻率變化時fs為第s倍率時頻率(s=0.9, 0.95, 1.05, 1.1),定義頻率變化率計算公式為Δf=(fs-f1.0)/f1.0,計算結果見圖6。由圖6得:節點單元剛度分別變化時,M16-Φ32×2.15、M24-Φ48×3.5、M24-Φ60×3.5均對自振頻率影響較大,而M27-Φ89×3.75的剛度變化對基頻影響較小,其它階頻率規律與此類似。因此在修正時可不考慮M27-Φ89×3.75的影響,即節點單元剛度取值仍據文獻[9]結果確定。 本文利用神經網絡技術對M16-Φ32×2.15、M24-Φ48×3.5、M24-Φ60×3.5對應的三種螺栓球節點單元剛度折減系數進行修正。在文獻[9]結果(a1=0.524,a2=0.466,a3=0.317)基礎上,選a1=0.5,a2=0.45,a3=0.30(本文稱為基準系數)為基準進行優化,以期找到更接近實際結構的折減系數。為此對修正參數容許變化范圍限值,設定基準系數a1,a2,a3的允許變化區間為[-20%,20%],在此范圍內尋優。 圖6 不同節點連接類型剛度變化對基頻影響 結構頻率測試方便且較準確,能反應結構整體的動力特性。因此利用神經網絡對結構修正時作為較好的輸入參數[14]。但空間網格結構龐大,在結構損傷識別診斷時振型變化對損傷更敏感。針對空間網格結構特點,須合理運用兩參數組合構造輸入參數。修正后模型不僅要求頻率接近,且應保證MAC值盡可能接近于1。本文采用頻率與振型組合參數(Combined Parameters of Frequency and Mode,CPFM)為神經網絡輸入: CPFM={FRE1,FRE2,…,FREm;DF1,DF2,…,DFn} (2) 式中:m為所用頻率階數;n為所用振型階數;FREi(i=1,2,…,m)為所用第i階頻率;DFi=(φi1,φi1,…,φiq,)為第i階模態對應q個測試自由度歸一化振型向量,計算式為: (3) 式中:φij為第i階模態對應于j個測試自由度分量。 據空間網格結構實際工程及試驗網殼模態測試經驗,為保證實測數據的有效性,構造參數CPFM時原則上規定頻率不宜超過前五階(m≤5)、振型不宜超過前三階(n≤3),且盡量選此范圍內振動形式較簡單階次。 圖7 修正方法流程圖 綜上分析,考慮節點半剛性螺栓球網格結構模型修正流程見圖7。按圖7,以a1=0.5,a2= 0.45,a3=0.30為基準系數,據以上提出的分步修正策略,通過試驗網殼半剛性模型建立組合參數CPFM與節點單元剛度折減系數關系樣本庫A、B,再通過訓練GRNN(即以組合參數CPFM為輸入,結構節點單元剛度折減系數為輸出),最終可得試驗網殼節點單元折減系數識別的逆向神經網絡模型。將實測的前四階頻率與一、二階Y、Z向9個位置(圖1中黑色實心圓)18個傳感器振型分量構造CPFM(40×1矩陣)為GRNN網絡輸入,二次修正后的剛度折減系數為[0.594,0.536,0.241],代入試驗網殼半剛性模型進行模態計算,結果與實測值分析見表3。由表3看出: (1) 與表2相比,各階次頻率誤差均有大幅度減小,且第一階振型符合良好,反映結構真實動力特性較準確,證明本文所用修正方法合理有效。 表3 模型修正結果 (2) 因空間網格結構自身龐大、激勵能量有限導致低階模態易被激發,且一階振型為簡單平動,測試結果較符合;三階振型較復雜,輸入參數未考慮三階振型影響,導致修正后三階模態誤差較大。 (3) 修正后仍存在誤差,原因如假設桿件幾何尺寸、材料彈性參數均可精確獲得因而未考慮動力敏感度低的M27-Φ89 ×3.75剛度修正;試驗中也存在加工、安裝精度等誤差及測試環境干擾。 本文基于實測模態數據對試驗網殼進行有限元模型修正研究,結論如下: (1) 提出的建立帶有剛度可調節點單元的半剛性模型對螺栓球節點單元剛度折減系數進行有限元模型修正新方法,通過試驗網殼模型修正,該方法有效性得以驗證。與傳統矩陣型、參數型修正方法相比,該方法物理意義明確、計算量小、精度高。 (2) 針對空間網格結構節點、桿件眾多等特點,所用分步修正策略可效避免神經網絡的數據爆炸及非線性能力降低等問題,可增強其在空間網格結構中的適用性。 (3)對實際工程監測中布置測點有限問題,用結構有限測點低階頻率及振型分量構造神經網絡輸入參數CPFM,通過試驗網殼模型修正證明其有效性。本文所提修正方法適合于不完備的模態數據,具有一定工程應用價值。 參 考 文 獻 [1]OU Jin-ping, LI Hui. Structural health monitoring in mainland China: review and future trends[J]. Structural Health Monitoring,2010,9(3):219-231. [2]Samali B, Dackermann U, Li J C. Ocation and severity identification of notch-type damage in a two-storey steel framed structure utilising frequency response functions and artificial neural network[J]. Advances in Structural Engineering , 2012, 15 (5) :743-757. [3]Zapico J L, González-Buelga A, González M P, et al. Finite element model updating of a small steel frame using neural networks[J].Smart Materials and Structures, 2008, 17(4): 045016-045027. [4]瞿偉廉, 譚冬梅, 汪 箐, 等. 基于神經網絡的大型空間網架結構的有限元模型修正[J]. 地震工程與工程振動,2003,23(4):83-89. QU Wei-lian, TAN Dong-mei, WANG Jing, et al. Finite element model correction of large space truss structure based on neural net[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 83-89. [5]劉 暉, 瞿偉廉, 王錦文, 等. 基于有限測點信息的大型空間網架結構智能工作狀態評估技術研究[J]. 土木工程學報, 2007, 40(12): 52-58. LIU Hui, QU Wei-lian, WANG Jin-wen, et al. A study on estimation of the intelligent work status of large space truss structures based on limited measurement information[J]. China Civil Engineering Journal,2007, 40(12): 52-58. [6]何浩祥, 閆維明, 王 卓. 基于子結構和遺傳神經網絡的遞推模型修正方法[J]. 工程力學, 2008,25(4):99-105. HE Hao-xiang,YAN Wei-ming,WANG Zhuo. Stepwise model updating method based on substructures and GA-ANN[J]. Engineering Mechanics, 2008, 25(4):99-105. [6]蔡艷平,李艾華,石林鎖.基于盲解卷積的柴油機振動信號的分離研究[J].振動與沖擊,2010,29(9): 38-41,240. CAI Yan-ping,LI Ai-hua,SHI lin-suo.Separation of diesel engine vibration signals based on the blind deconvolution[J].Journal of Vibration and Shock, 2010,29(9):38-41,240. [7]周曉峰,楊世錫,甘春標.相關機械振源的盲源分離方法[J].振動與沖擊,2012,31(14):60-63. ZHOU Xiao-feng,YANG Shi-xi,GAN Chun-biao. Blind source separation of statistically correlated sources[J].Journal of Vibration and Shock, 2012, 31(14):60-63. [8]Comon P.Independent compoment analysis ,a new concept[J].Signal Processing, 1994,36(3):287-314. [9]Zhukov L,Weinstein D,Johnson C.Indepentent component analysis for EEG source location[J]. IEEE Engineering in Medicine and Biology Magazine,2000,19(3):87-96. [10]Hyv?rinen A, Karhinen J, Oja E. Independent component analysis[M]. New York:Wiley,Chichester,2001. [11]GrayW C.Variablenom deconvolution[D]. Standford:PhD Dissertation of Stanford, 1979. [12]Choi S, Cichocki A.On-line sequential multichannel blind deconvolution:a deflation approach[C].Proceedings of the 8th IEEE DSP Workshop,Utath,USA,1998:159-162. [13]Liu X H,Robert B R, J r me A.Blind separation of internal combustion engine vibration signals by a deflation method[J].Mechanical Systems and Signal Processing,2008,22(5):1082-1091 . [14]Liu X H, Robert B R.Blind source separation of internal combustion engine pistion slap from other measured vibration signals[J].Mechianical Systems and Singal Processing, 2005, 19(6): 1196-1208. [15]Hao Zhi-yong, JIN Yan,YANG Chen.Study of engine noise based on independent component analysis[J]. Zhejiang University Science A,2007,8(5):772-777. [16]Jerome A.Blind separation of vibration components:principles and demonstrations[J]. Mechanical Systems and Singal Processing, 2005,19(6):1166-1180.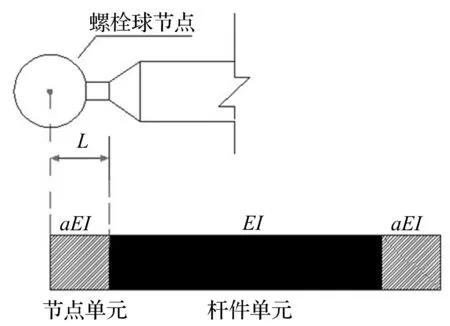
2.2 修正參數確定
2.3 神經網絡輸入參數確定
2.4 基于GRNN網絡的分步修正策略
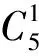
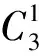
3 基于實測數據的試驗網殼模型修正
4 結 論

