拉矯機(jī)帶鋼反彎曲率的計(jì)算方法

鄭祥臣 馬瑞杰 徐啟發(fā)

(中冶南方工程技術(shù)有限公司 湖北武漢430223)

?

拉矯機(jī)帶鋼反彎曲率的計(jì)算方法

鄭祥臣①馬瑞杰 徐啟發(fā)

(中冶南方工程技術(shù)有限公司 湖北武漢430223)

對(duì)于拉伸矯直機(jī)，帶鋼在矯直機(jī)輥?zhàn)由系那拾霃降挠?jì)算尤為重要，只有確定了該曲率半徑，才能進(jìn)一步計(jì)算帶鋼的反彎曲率、彈復(fù)曲率和殘留曲率，進(jìn)一步計(jì)算帶鋼的平直度。假定帶鋼在矯直輥上的曲線為拋物線，給出帶鋼反彎曲率半徑的計(jì)算方法，并且進(jìn)一步討論矯直輥輥?zhàn)又睆降挠?jì)算方法。

拉矯機(jī) 拋物線 彈塑性變形 反彎曲率

1 背景知識(shí)

平直度是評(píng)價(jià)金屬板帶質(zhì)量的重要指標(biāo)之一，拉矯機(jī)是消除帶材平直度曲線，改善板形的關(guān)鍵設(shè)備，對(duì)帶材質(zhì)量影響極大[1]。之前，我國各有色冶金，鋼鐵冶金中所用的拉矯機(jī)多數(shù)依靠進(jìn)口，近幾年來，國內(nèi)開始嘗試國產(chǎn)化，但是對(duì)于拉矯機(jī)拉伸彎曲過程的理論分析還不夠深入，影響了矯直機(jī)的發(fā)展，用戶對(duì)于要求較高的拉矯機(jī)，還不放心使用國產(chǎn)化的設(shè)備。

對(duì)于帶鋼在拉矯機(jī)矯直輥上的模型，崔甫在其專著中就直接采用了矯直輥半徑作為反彎曲率半徑，這樣顯然是做了很大的近似[2]，對(duì)于其他論文和專著中有采用圓弧，拋物線，以及多次方方程擬合曲線等等[3-4]，根據(jù)作者在型材以及多輥式矯直機(jī)中的計(jì)算與實(shí)踐證明，采用拋物線跟實(shí)際比較吻合。

2 建立拉矯機(jī)矯直輥處帶鋼數(shù)學(xué)模型

2.1 拉矯機(jī)矯直輥處帶鋼數(shù)學(xué)模型

條件假設(shè)，首先根據(jù)現(xiàn)場(chǎng)經(jīng)驗(yàn)，帶鋼每經(jīng)過一次反彎，其張力變化一般不會(huì)超過2%，因此假設(shè)張力的變化對(duì)拋物線模型沒有影響，拋物線的頂點(diǎn)位于帶鋼角平分線上，如圖1中D點(diǎn)。

圖中O為矯直輥圓心，JE為受力切線，DG被認(rèn)為帶鋼所形成的拋物線，拋物線DG與受力切線JE的交點(diǎn)為G，拋物線在G點(diǎn)的斜率與JE斜率相等。圖中以D點(diǎn)為圓心，Dx為橫坐標(biāo)軸，Dy為

圖1 拉矯機(jī)拉矯模型拋物線示意圖

為縱坐標(biāo)軸，建立平面直角坐標(biāo)系。

2.2 以模型為基礎(chǔ)推導(dǎo)計(jì)算公式

在平面直角坐標(biāo)系中，假設(shè)拋物線方程為：

y=ax2

對(duì)于帶材彎曲時(shí)的彎矩為[2]：

(1)

(2)

(3)

式中 a—不為零的常數(shù)； M—帶鋼的彎矩； B—帶鋼寬度； H—帶鋼厚度； σs—帶鋼屈服強(qiáng)度； E—帶鋼彈性模量； Ht—帶鋼彈性區(qū)厚度； At—帶鋼反彎曲率半徑的倒數(shù)。

對(duì)于拋物線頂點(diǎn)的曲率半徑的計(jì)算如下：

假設(shè)拋物線頂點(diǎn)是一個(gè)微小的圓，則拋物線上一點(diǎn)也在圓上，假設(shè)改點(diǎn)為(dx，adx2)，而改點(diǎn)又在圓上，故：

式中R—矯直輥頂點(diǎn)曲率半徑；dx—拋物線頂點(diǎn)在x軸上的坐標(biāo)值。

忽略高次無限小，則：

(4)

由式(1)～(4)得出：

(5)

帶鋼理論切線方向與橫坐標(biāo)夾角為β，則G點(diǎn)斜率為：

2ax1=tanβ

(6)

過G點(diǎn)且斜率為2ax1的方程為：

則坐標(biāo)原點(diǎn)到該線的距離即為力臂L：

(7)

根據(jù)力對(duì)坐標(biāo)原點(diǎn)彎矩平衡，可知：

(8)

式中F—帶鋼張力。

由式(6)、(8)可得

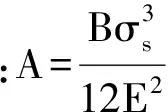
2.3 討論矯直輥輥?zhàn)又睆降挠?jì)算方法

由以上假設(shè)可以看出，要使帶鋼按照拋物線的方式存在，則必須使該拋物線除坐標(biāo)原點(diǎn)外不能與矯直輥輥?zhàn)佑薪佑|，假設(shè)輥?zhàn)影霃綖镽1，則矯直輥輥?zhàn)拥姆匠虨椋?/p>

由拋物線方程：

y=ax2

以上兩方程聯(lián)立，要使該方程無解，則需：

由以上可以看出，矯直輥半徑必須小于帶鋼在矯直輥頂點(diǎn)處的曲率半徑。

3 實(shí)例計(jì)算

以某拉矯機(jī)模型，給定參數(shù)，計(jì)算其反彎曲率半徑

B=1000mm—帶鋼寬度；

σs=500MPa—帶鋼屈服強(qiáng)度；

E=206000MPa—帶鋼彈性模量；

H=2mm—帶鋼厚度；

β=10o—帶鋼切線角度；

F=100000N—帶鋼張力。

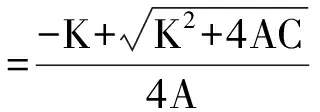
4 結(jié)論

從以上模型，可以很簡單的計(jì)算出帶鋼經(jīng)過矯直輥時(shí)的反彎曲率，且反彎曲率的計(jì)算除了跟帶鋼的材料屬性有關(guān)系外，還跟帶鋼張力和帶鋼在輥?zhàn)由系陌怯嘘P(guān)。

從以上也可以定性的計(jì)算矯直輥直徑的最大值，為將來矯直輥選型計(jì)算提供理論依據(jù)。

[1]傅玉永.拉伸彎曲矯直機(jī)輔助設(shè)計(jì)與控制仿真系統(tǒng)的研究與開發(fā)[D].重慶大學(xué)，2006.

[2]崔甫.矯直原理與矯直機(jī)械第二版[M].北京：冶金工業(yè)出版社，2005:7-24，382-390.

[3]上海機(jī)電工業(yè)管理局.寶鋼2030mm冷軋機(jī)組機(jī)械設(shè)備關(guān)鍵技術(shù)的探討[M].上海：上海科技文獻(xiàn)出版社，1988:3，281-290.

[4]日本塑性加工工學(xué)會(huì)編.矯正加工——板，管，棒，線た真直すぐにゐ方法[M].東京：コロナ社，1992：91-106.

Calculate Method of the Strip Reverse Curvature for Tension Leveller

Zheng Xiangchen Ma Ruijie Xu Qifa

(WISDRI Engineering & Research Incorporation Limited, Wuhan 430223)

For tension leveler, it’s especially important to calculate the curvature radius of strip on the straightener roll. Only to determine the radius of curvature, then it’s possible to calculate reverse curvature, elastic recovery curvature and residual curvature and the flatness of the strip. This paper assumes that the curve is parabola on the straightener roll, gives the method to calculate the curvature radius of strip and discusses the method to calculate the diameter of straightener roll.

Tension leveller Parabola Elastic-plastic deformation Reverse curvature

鄭祥臣，男，1986年出生，2010年畢業(yè)于東北大學(xué)機(jī)械電子工程專業(yè)，碩士，工程師，主要研究方向：矯直理論研究和設(shè)備設(shè)計(jì)、冷軋帶鋼處理線的研究與設(shè)計(jì)

TG333.23

A

10.3969/j.issn.1001-1269.2014.01.005

2013-09-23)