萊鋼鋸機萬向接軸故障分析

李雪濤

（山鋼集團萊鋼設備檢修中心 山東萊蕪 271104）

1 前言

鋸機作為冶金軋材生產線的主題設備，其穩定的工作狀態至關重要，但在實際生產過程中，經常出現鋸機震動過大造成軋件切斜、傳動接軸十字包斷裂等事故，影響生產的穩定運行，因此依據原設計，結合現場實際，對接軸設計進行適應性改造。

2 鋸機萬向接軸故障分析

萊鋼軋材生產線主要使用型號為SWP250的進口萬象接軸，作為鋸機設備的傳動部件。萬向接軸在生產中的常見故障主要是運行中出現動平衡破壞，震動過大，軋件切斜，萬向節十字軸處出現裂紋或斷裂等現象，這些問題是萬向節傳動形式當中典型的疲勞破損現象引起的。

圖1 十字軸總成結構圖

3 鋸機萬向接軸受力分析

鋸機萬向接軸采用十字軸式剛性萬向節傳動形式。從動十字軸旋轉的角度是不均勻的。其運動學特點簡單分析如下（如圖2所示）。

設主動十字軸與從動十字軸夾角為α，主動十字軸以等角速度ω1旋轉，十字軸萬向節轉動半徑為r。先看兩個特殊位置的速度：

1）主動十字在垂直位置，并且十字軸平面與主動軸垂直，如圖2 a）所示。主動叉與十字軸連接點a的線速度Va在十字軸平面內，Va＝ω1r；從動叉與十字軸連接點b的線速度Vb在與主動叉平行的平面內，并且垂直于從動軸，點b的線速度Vb可分解為在十字軸平面內的速度V＇b和垂直于十字軸平面的速度Vb″。由速度直角三角形可看出在數值上Vb＞V＇b。十字軸是對稱的，oa＝ob。當萬向節傳動時，十字軸是繞O點轉動的，其上a、b兩點于十字軸平面內的線速度在數值上應相等，即V＇b＝Va，因此Vb＞Va。因此可知，當主從動叉轉到所述位置時，從動軸的轉速大于主動軸的轉速。

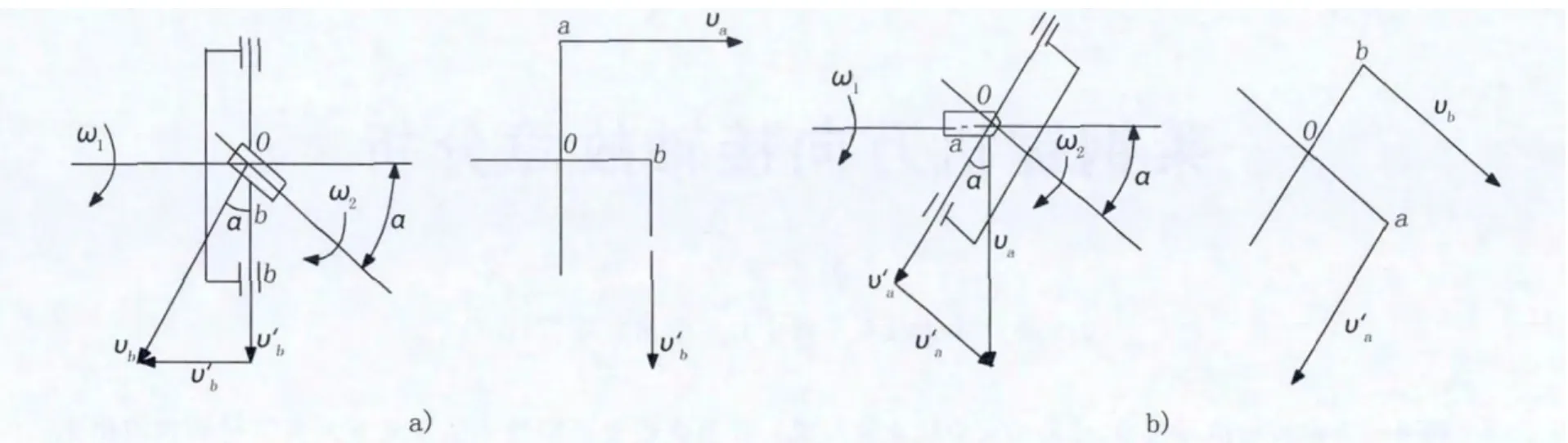
圖2 萬向節運動學圖示

2）主動叉在水平位置，并且十字軸平面與從動軸垂直，如圖2b）所示。此時主動叉與十字軸連接點a的線速度在平行于從動叉的平面內，并且垂直于主動軸。線速度Va可分解為在十字軸平面內的速度V＇a和垂直于十字軸平面的速度Va″，根據同樣道理，在數值上，Va＞V＇a，而V＇a＝Vb，因此，Va＝Vb即當主從動叉轉到所述位置時，從動軸轉速小于主動軸轉速。

3）顯然，由a點，Va＝ω1r，V＇b＝Vbcosα＝ω2rcosα，可知

ω1＝ω2cosα或ω2＝ω1／cosα

由（2）點，V＇a＝Vacosα＝ω1rcosα，Vb＝ω2r，可知

ω1＝ω2／cosα或ω2＝ω1cosα

即當主動十字軸以等速度ω1轉動，主動叉由垂直位置轉到水平位置時，從動十字軸的角速度由大于主動十字軸角速度的最大值ω1／cosα變化至小于主動叉角速度的最小值ω1cosα。主動軸再轉90°，從動軸的角速度又由最小值變至最大值。從動軸角速度的變化周期為180°。即在一圈內變化兩次，而且從動軸不等速的程度是隨兩軸間夾角α的加大而加大。

4）剛性十字軸式萬向節從動軸以每周變化兩次的周期進行不等角速度旋轉，其旋轉的角加速度會引起較大的慣性力矩，從而可能引起傳動系統的扭轉振動，剛性十字軸式萬向節傳動中主動十字軸扭矩M1與從動十字軸扭矩M2的變化關系即動力學特征。簡要說明如下：

5）如果不計萬向節里的摩擦損失，即有M1ω1＝M2ω2由萬向節運動學特征可知，當ω1以等速旋轉時，隨萬向節旋轉所處位置不同，從動軸角速度ω2在ω1／cosα至ω1cosα之間不均勻變化。顯然，當萬向節主動叉處在垂直位置，萬向節十字軸平面與主動軸垂直時，如3a）圖所示，從動叉軸上的扭矩最小，即M2min＝M1cosα。當萬向節主動叉在水平位置，萬向節十字軸平面與從動叉軸垂直時，從動叉軸上的扭矩最大，即M2max＝M1／cosα。

6）主動叉對十字軸的作用力矩，除主動扭矩M1之外，還有作用在主動叉平面的彎曲力矩M＇1。同理，從動叉對十字軸也作用有從動軸反扭矩M2和作用在從動叉平面的彎曲矩M＇2。

如圖3a）所示，由于M1作用在十字軸平面，M＇1必為零，因M2的作用平面與十字軸不共平面，必有M＇2存在。向量M＇2是垂直于M2的，合向量M＇2＋M2指向十字軸平面的法線方向，而與M1方向相反，大小相等。由力矩向量三角形可知M＇1＝M1sinα。當萬向節主動叉處于水平位置，十字軸平面與從動軸垂直時，同理可知M＇2＝0主動叉上的附加彎曲力矩M＇＝M1tgα，如圖3b）所示。

由此可見，附加彎曲力矩的數值零與以上兩公式所表示的最大值之間變化的，其變化周期為180°。即每轉變化兩次。附加彎矩可在萬向節主、從動軸支承上引起周期性變化的徑向載荷，并有可能激起支承的振動。

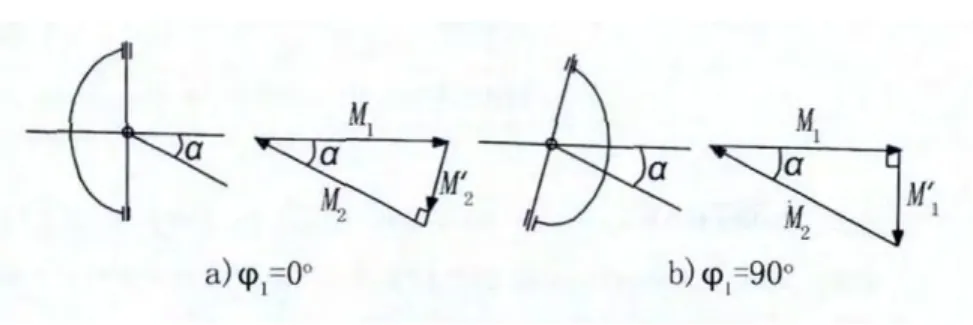
圖3 十字軸萬向節的力矩平衡

7）萬向接軸在某個工作角度下，在十字軸對稱軸的平面內將產生二次力偶。二次力偶產生在十字軸的軸心交點，形成力偶矩使十字軸彎曲，使滾針軸承和十字軸受到附加的二次載荷。根據圖4、圖5進行受力分析

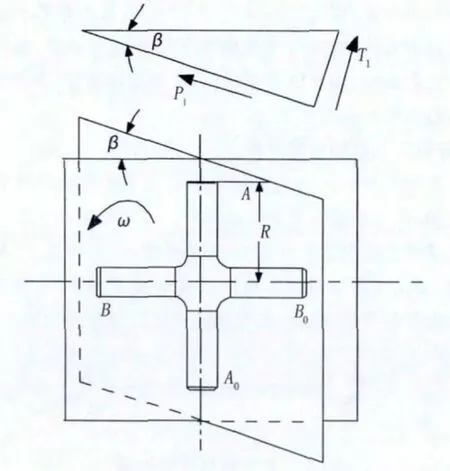
圖4 驅動軸AAO受力分析

驅動軸AA0受力分析：

作用于十字軸A A0上的力P1、T1：

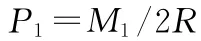
式中M1—驅動軸力矩；

P1—作用于十字軸上的力；

R—力的作用半徑。

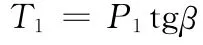
式中T1—作用于驅動軸軸承座上的二次載荷；

β—傾角。

二次載荷T1形成的力偶矩為：

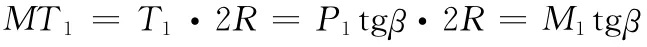
當被動軸B B0位于軸承座的旋轉軌跡交線時，受力分析如圖5。

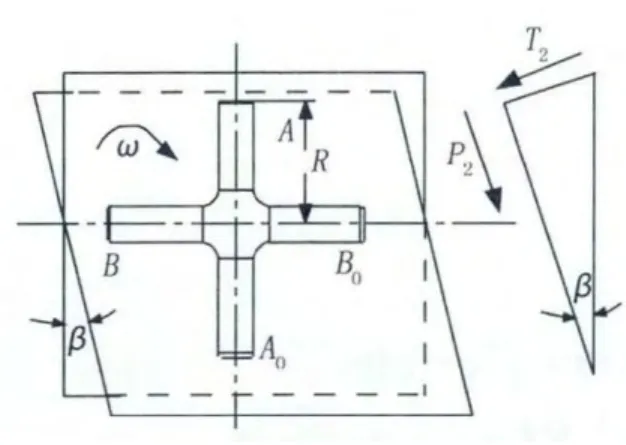
圖5 BB0驅動軸受力分析

同理可計算出作用在十字軸BB0上的二次載荷T2：

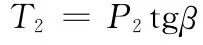
又因

二次載荷T2及形成的力偶矩為：

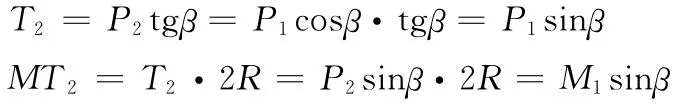
式中M2—從動軸力矩；

P2—作用于十字軸上的力；

R—力的作用半徑。

根據計算結果分析，接軸每旋轉90°，驅動軸和從動軸的二次載荷力矩從零到最大，當十字軸的中心線與軌跡交線相重合時達到最大值。此外，每當轉過180°時，作用在十字軸上的力改變方向。

4 萬向接軸的受力計算

圖6為萬向接軸力學模型簡圖。

圖6 萬向接軸力學模型簡圖

根據瞬時功率相等的原則，從動軸上的轉矩為

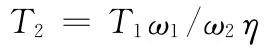
當φ1＝90°或270°時從動軸上的轉矩達到最大值

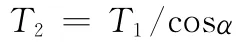
當φ1＝0°或180°時從動軸上的轉矩達到最小值

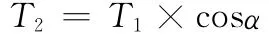
當軸間角α不等于零時，由于主從動軸的回轉平面不在同一平面，因而產生附加轉矩，其值與主動軸轉角和軸間角的大小有關，即當φ1＝90°或270°時，作用在主動軸叉上的附加彎矩達到最大值。

式中φ1—主動軸和中軸的轉角；

α—主動軸與中軸的軸間角；

ω1、ω2—主動、從動軸的角速度。

由于傳動軸轉速波動引起的附加慣性轉矩可按經驗公式將計算出的最大轉矩乘以系數1.1。

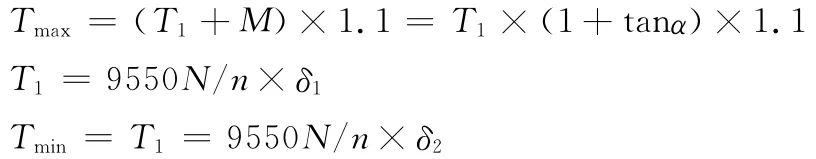
式中δ—電機輸出系數。

計算結果為

同時對鋸機驅動電機的工作電流進行隨機抽查，通過電機工作電流對照電機的電流、功率曲線推算矯鋸機電機輸出轉矩，見表1。

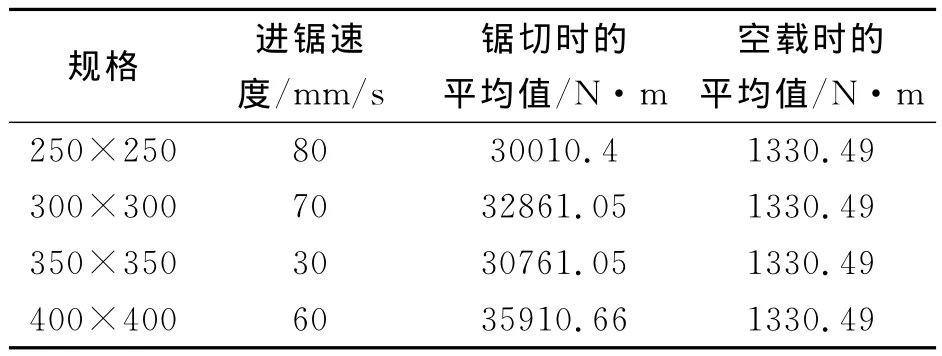
表1 驅動電機技術參數

通過表1對照，計算結果與實際輸出轉矩基本相符，證明計算結果是正確的。

5 萬向接軸的校核

鋸機萬向接軸在鋸切時受交變載荷，在強度校核中取萬向接軸疲勞轉矩23000N·m。通過對照現場萬向接軸輸入轉矩計算值，萬向接軸在鋸切時的轉矩最大值遠大于萬向接軸疲勞轉矩小于萬向接軸的額定轉矩。當工作轉矩大于萬向接軸的疲勞轉矩時，萬向接軸就會發生疲勞損壞，但不會立即表現出來，只有疲勞損壞累積到一定程度，萬向接軸才會發生斷裂。因此將矯直機萬向接軸更換為國產SWP285（公稱轉矩90kN·m，疲勞轉矩45kN·m，軸線轉角15°）。

6 結語

通過校核，改進原設計中存在缺陷的地方，提高設備的運行穩定性，經過適應性改造，很好適應了現場生產需要。

［1］張杰，張敏中.三球銷式等速萬向節的受力分析，江蘇理工大學學報，1998（5）.

［2］王望予.汽車設計（第四版），北京：機械工業出版社，2011.

［3］石寶樞.等速萬向節傳動軸的可靠性設計［J］.軸承，1998（5）.