接收機自主完好性監測技術研究
婁上月,辛 吉,洪詩聘,李建華,李 峰
(1.北京自動化控制設備研究所,北京 100074;2.空軍駐某院軍代表室,北京 100000)
0 引言
隨著GPS導航技術應用領域的多樣化,標準定位服務 (Standard Positioning Service,SPS)已無法滿足用戶對高精度、高可靠性的需求,這就需要對系統的定位精度、連續性、可用性和完好性有更加嚴格的要求。完好性是其中具有非常重要意義的指標之一,它是指衛星定位誤差超過允許極限的時候,在一定時間內向用戶發出告警的能力。從數學本質上來說,完好性就是對系統所提供信息正確性的置信度測量。
當前完好性監測的主要方法分為兩種:一種是GPS完好性通道 (GPS Integrity Channel,GIC);另一種就是接收機自主完好性監測。RAIM由于其可以不依賴外部增強系統而獨立工作,逐漸成為了完好性監測的主要工作方法和研究熱點之一。
對于導航定位來說,完好性異常一旦發生所造成的后果是非常嚴重的,所以對完好性監測技術的研究是有其重要的安全意義和研究價值的。
目前國內對完好性監測的研究尚處于初始階段,對完好性監測性能的綜合研究非常少,與國外相比還存在一定的差距。本課題以最小二乘法對接收機自主完好性監測的基本公式進行了推導和分析,以奇偶矢量法在實際工程應用中驗證了RAIM算法的正確性和可行性,并提出了一種新的故障衛星排除算法-RMS比較法,通過理論推導和實際工程反復驗證了此算法的有效性。
1 最小二乘法進行衛星故障檢測
傳統的RAIM算法是利用冗余觀測量來進行故障的檢測和識別,主要有奇偶空間法、最小二乘殘差法、距離比較法等。這里以最小二乘殘差法為例,簡介其檢測原理。
GPS測量方程式如下所示:

式中x是4×1的位置矢量和鐘差;y是n×1的偽距殘差矢量;H為n×4階觀測矩陣,表示由各衛星到用戶接收機的方向余弦矢量和含1的第四列構成的線性化矩陣;ε為n×1的測量誤差矢量;n為觀測衛星個數。
最小二乘估計的指標是:使觀測量Z與其相應的估計值Hx之間的差的平方和最小。將該結果與y的作差,得到的結果為距離殘差

矢量w:
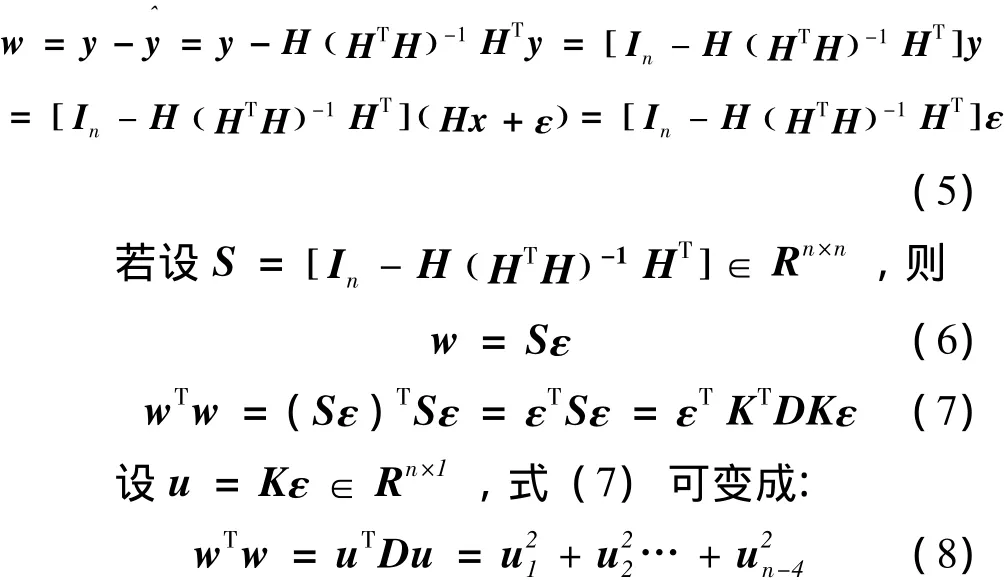
當ε~N(0,σ2),由于K為正交矩陣,u=Kε
0是關于ε的線性函數,則根據正態變量的線性變換不變性可知,u=Kε∈Rn×1服從均值為0,方差為Inσ20的正態分布。則根據χ2分布的概念可知,歸一化變量滿足自由度為n-4的χ2分布。

根據假設條件,當無故障衛星存在時,如果出現檢測警告,則為誤警,當誤警率PFA給定時,可以確定檢測門限值:

圖1為MATLAB軟件仿真出來故障檢測效果圖,數據來源是2011年3月28日在美國國家大地測量局 (National Geodetic Survey,NGS)專業網站上發布的GPS導航文件和觀測文件,由于是真實的導航文件,其衛星并沒有發生故障,所以為了驗證最小二乘法正確性,人工在觀測文件中加入了6個衛星故障,每隔200個歷元加入一個,故障幅值為3σ,σ =4m。
2 奇偶矢量法進行故障檢測
對于線性化GPS測量方程Z=HX+ε,若當前可見衛星中無故障星,則觀測噪聲ε~N(0,σ2)
0為白噪聲誤差;若當前可見衛星中存在故障星,則觀測誤差ε是包含噪聲誤差和故障誤差的混合誤差,滿足方程Z=HX+ε+Tiq,其中Tiq表示第i顆可見衛星為故障星,T= [0 … 1 …0]T,故障幅值為q。因此可以將觀測量Z轉換到奇偶空間中,將觀測誤差提取處理,根據觀測誤差在有無故障情況下的不一致性進行故障檢測。
若選擇矩陣V滿足 VH=0,則存在如下變換:
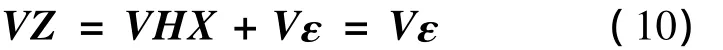
將滿足條件的矩陣V稱之為奇偶變換矩陣,則根據式 (10)可以發現,可以通過奇偶變換矩陣將觀測誤差提取出來進行一致性檢測。
將矩陣H進行QR分解可以得到:



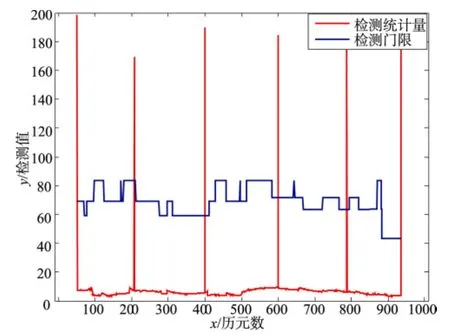
圖1 最小二乘法故障檢測圖Fig.1 The scheme of fault detection by least square method
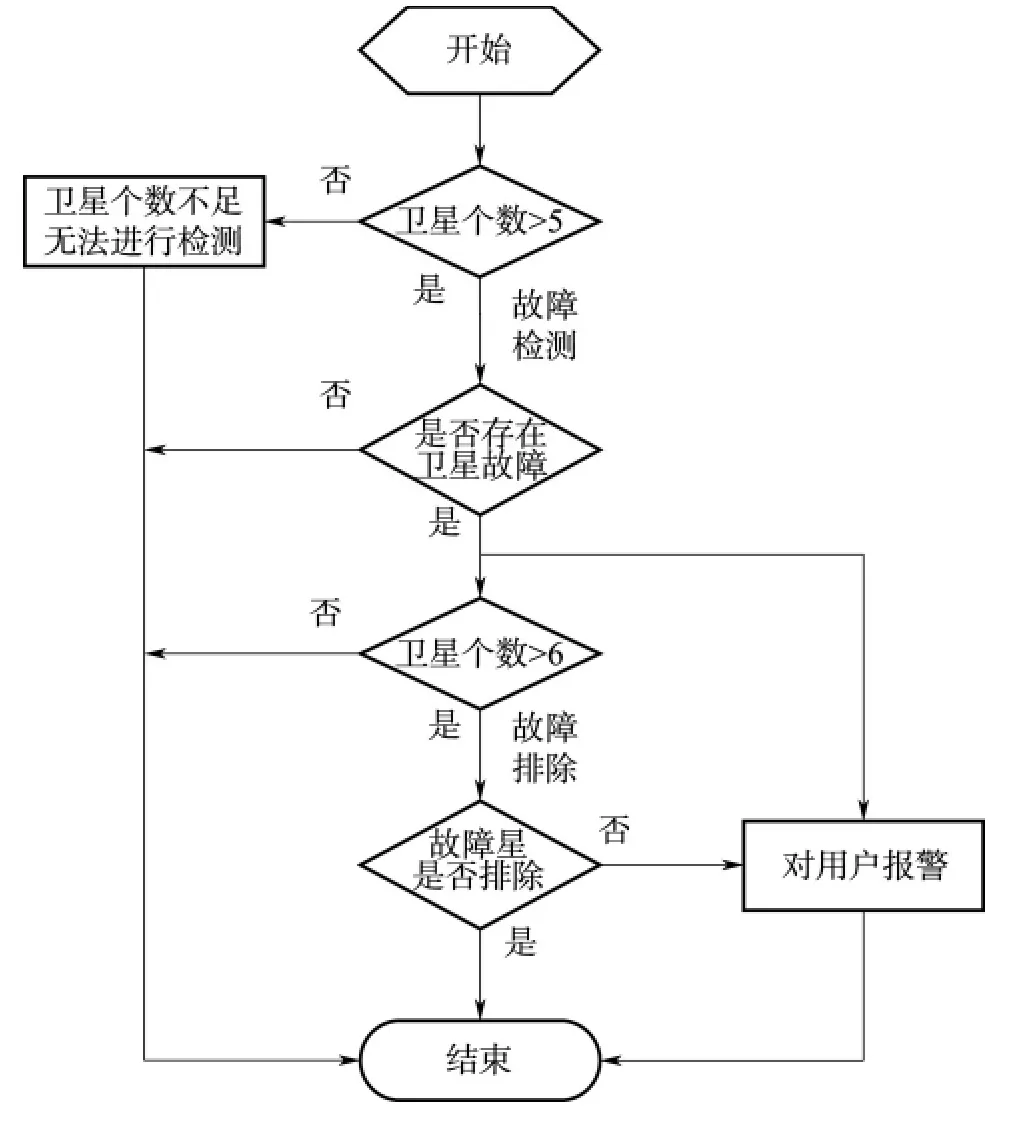
圖2 RAIM算法檢測流程圖Fig.2 The flow chart of RAIM method detection
奇偶矢量法與最小二乘殘差法在實際應用過程中具有等效性,但是由式 (6)和式 (14)進行比較可以發現,距離殘差矢量w的計算需要多個矩陣相乘,而奇偶矢量p的運算只需要進行QR分解和一步矩陣相乘,所以奇偶矢量法具有更少的計算量,更能夠滿足高精度導航定位對TTA的要求;同時奇偶矢量法簡單易懂,在實際工程中應用更為簡便,是美國航空無線電技術委員會 (RTCA)推薦使用的算法。
使用MATLAB中的cputime()函數對奇偶矢量法和最小二乘法進行故障檢測過程進行計時,選取其中2000個歷元進行了事后處理,電腦的CPU主頻為2.5GHz,其他所有檢測條件均相同,其結果如下表:
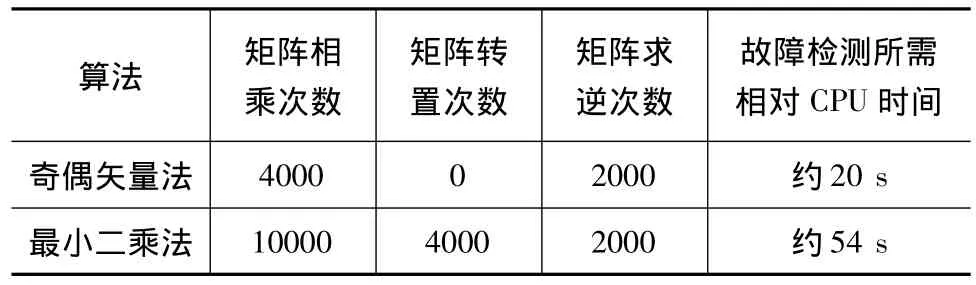
表1 兩種算法的計算量比較Table.1 Contrast with calculation time of differrent algorithms
3 基于RMS比較法的單衛星故障排除
由于傳統奇偶矢量法進行故障檢測和排除是利用當前時刻的測量數據的統計特性進行相關計算,對冗余變量個數有嚴格要求,因此,該算法在冗余變量個數過少的情況下是不能高效率的完成衛星故障檢測與識別的,極大的限制完好性監測性能,考慮到此算法在實際工程應用中的局限性,本文提出了一種新的故障識別算法——RMS比較法,即通過對當前全部觀測量的偽距殘差進行系列運算,識別并排除故障星。
RMS比較法具體實現流程:將每顆星偽距殘差進行由大到小排序,而后從前到后每4個點計算一個殘差的RMS值,如果衛星是n個,則得到n-3個殘差RMS值。找出殘差RMS最小的組合,求得該組合的平均值,此平均值作為故障識別的門限值,然后將每顆星的殘差值與求得的平均值做比較,大于門限的衛星即是有故障的衛星。RMS比較法流程圖如圖3所示。
均方根體現的是數據趨近于均值的穩定性,RMS最小組合的均值應該是穩定性最好組合的均值,是最接近總體數據均值的,因此使用此均值作為門限應該是比較準確的。此算法的優點在于計算量小,單純對偽距殘差值進行排序比較,沒有復雜的矩陣計算,在DSP程序運行過程中不會占用過多資源;簡單易懂,實現容易,此算法可以算是傳統距離比較法的簡單運算,但是比之前算法更加精妙;不是使用冗余變量一致性進行運算,可以彌補傳統算法必須在可見星大于6顆的前提下才能進行故障識別的缺陷,在可見衛星不足的極限情況仍能有效的進行故障排除,極大增強了完好性監測性能。
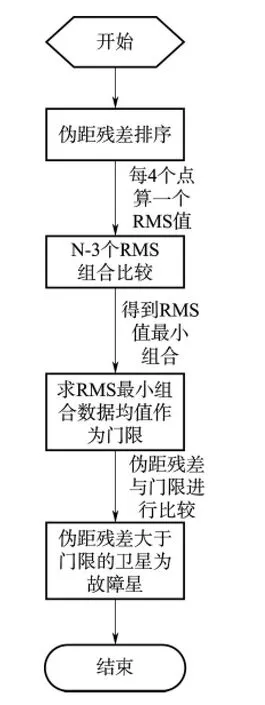
圖3 RAIM算法檢測流程圖Fig.3 The flow chart of RAIM method detection
為了驗證RMS比較故障識別算法的正確性,在常規單星故障情況和少星情況下,在第3顆可見衛星上人為加入脈沖故障,其故障識別檢驗結果如下:
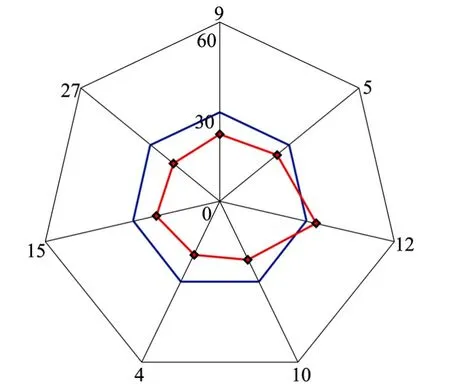
圖4 在常規情況下RMS比較法進行故障排除Fig.4 The fault identification of RMS in common practice
圖4為衛星故障識別圖,圖中橫向圈線為刻度線,縱向分割線表示當前歷元可見衛星號,紅色點線表示每顆衛星對應偽距殘差值,藍色粗線表示RMS最小組偽距殘差平均值,即排除算法門限值。由圖中可以發現,第3顆衛星對應偽距殘差值大于檢測門限,可以判斷當前歷元第3顆可見衛星,即12號衛星為故障衛星,與仿真初始設置相同。
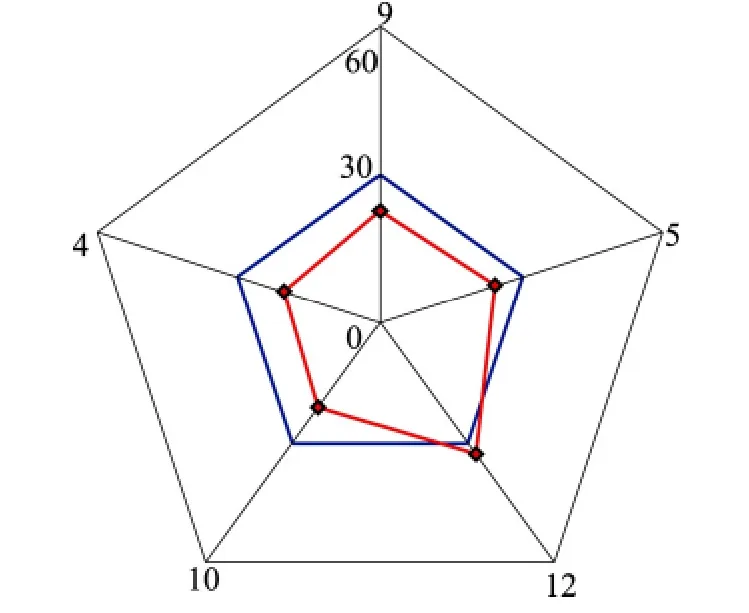
圖5 在少星情況下RMS比較法進行故障排除Fig.5 The fault identification of RMS in few satellite
圖5是在少星情況下進行的故障識別,人為限定選取歷元可見衛星個數為5顆,在傳統故障識別算法無法正常判斷出故障衛星的情況下,RMS比較法仍然能夠正常工作,并且正確識別出第3顆衛星為故障星,說明RMS比較法在故障識別過程中的優越性。
4 結論
本文從完好性監測的原理和本質出發,對傳統RAIM算法進行了詳細的公式推導并給出了仿真結果,對傳統算法正確性進行了驗證;對傳統算法的優點和缺陷進行了深入的分析,考慮到傳統算法在少星情況下無法正常進行故障檢測與排除的缺陷,提出了一種新的故障排除算法——RMS比較法。在傳統算法無法正常工作的少星情況下,該算法仍然能夠正確識別并排除故障衛星,充分體現了算法的正確性和優越性,具有較強的工程應用價值。
[1]趙琳,李亮,程建華,婁上月.用于識別雙星故障的RIAM算法[J].北京航空航天大學學報,2010,Vol.36 No.11:585-589.[Zhao Lin,Li Liang,Cheng Jian-hua,Lou Shang-yue.New RAIM algorithm for identifying simultaneous double-faulty satellites[J].Journal of Beijing University of Aeronautics and Astronautics,2010,Vol.36 No.11:1 -5].
[2]Young C L.Analysis of Range and Position Comparison Methods as a Means to Provide GPS Integrity in the User Receiver[C].Proceeding of ION 42th Annual Meeting,WA,USA,24-26,June 1986,pp:1-4.
[3]Parkinson B W,Axeled P.Autonomous GPS Integrity Monitoring Using the Pseudorange Residual[J].Navigation Journal of The Institute of Navigation,Summer 1988,35(2):255-274.
[4]Sturza M A.Navigation System Integrity Monitoring Using Redundant Measurement[C].Proceedings of the Third International Technical Meeting of the Satellite Division of the Institute of Navigation,Colorado Springs,CO,USA,19 -21 September 1990:437-443.
[5]郭睿,韓春好.接收機自主完好性監測的算法分析[J].測繪工程,2008,17(2):34-38.[GUO Rui,HAN Chunhao.Analysis of RAIM algorithm [J].ENGINEERING OF SURVEYING AND MAPPING.2008,17(2):34 -38.]
[6]Liang Li,Lin Zhao,Wei Cao and Shangyue Lou.A solution separation RAIM scheme based on adaptive clock-bias model[C].Proceedings of the 2010 IEEE International Conference on Information and Automation.June 20-23,Harbin China,pp:250-254.

