旋轉(zhuǎn)導(dǎo)彈電動舵機控制器超前補償方法

王 田

(北京理工大學(xué) 宇航學(xué)院，北京100081)

0 引言

導(dǎo)彈的滾轉(zhuǎn)方式可以克服由于發(fā)動機推力偏差、質(zhì)量偏心、導(dǎo)彈外形加工工藝誤差等干擾造成的不利影響，有效減小無控飛行段的散布。但是導(dǎo)彈采取旋轉(zhuǎn)體制帶來益處的同時，產(chǎn)生通道耦合，舵機控制系統(tǒng)延遲產(chǎn)生的控制誤差也因此增加。閆曉勇等人基于多變量的頻域設(shè)計方法研究解耦補償方式，往往將控制耦合與運動學(xué)耦合一并分析，補償方式類似［2］。而運動學(xué)造成的通道間耦合效應(yīng)往往很小，且隨轉(zhuǎn)速變化不大，所以如何有效消除控制耦合即舵機相角延遲，是雙通道控制解耦的重點。對于正弦控制指令跟蹤下的雙通道舵機系統(tǒng)，放寬部分時域指標(biāo)，控制器中加入動態(tài)補償環(huán)節(jié)，則可以達到頻率指標(biāo)提升，減小相角延遲，減弱控制耦合的目的。

本文針對舵機控制系統(tǒng)，建立數(shù)學(xué)模型，并進行正弦掃描辨識其模型參數(shù)，驗證其正確性。結(jié)合舵機控制系統(tǒng)開環(huán)傳遞參數(shù)，為控制器設(shè)計前端校正環(huán)節(jié)。并可在實際應(yīng)用中，對不同工作轉(zhuǎn)速動態(tài)調(diào)整中心頻率，以減小當(dāng)前工作狀態(tài)下的相角延遲。

1 舵機控制系統(tǒng)工作原理

1.1 舵機系統(tǒng)組成

舵機系統(tǒng)包括機械結(jié)構(gòu)和控制電路組成。機械結(jié)構(gòu)由無刷電機、傳動機構(gòu)、空氣舵及外加負載組成如圖1 所示;控制電路由控制器電路、外圍信號調(diào)理電路、驅(qū)動電路等組成。

電機是機械結(jié)構(gòu)中的核心部件，其工作原理動態(tài)過程可描述成如下:

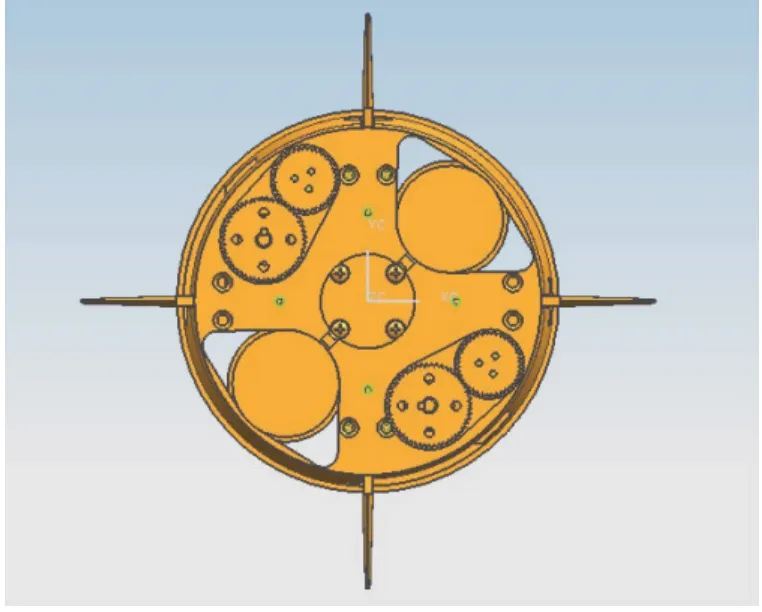
圖1 舵機結(jié)構(gòu)示意圖Fig．1 The scheme of actuator

其中，Te為電磁轉(zhuǎn)矩，Tl為折算到電動機軸上的負載轉(zhuǎn)矩，J 為等效在電動機軸上的轉(zhuǎn)動慣量，為電動機轉(zhuǎn)動角速度，B 為等效在電動機軸上的粘性阻尼系數(shù)，Kt為轉(zhuǎn)矩系數(shù)，Ke為反電動勢系數(shù)，Kg為減速裝置的減速比，u(t)為電機等效供電電壓，R 為電樞平均電阻，L 為相間電感，從等效控制電壓到輸出舵偏角的結(jié)構(gòu)框圖見圖2。

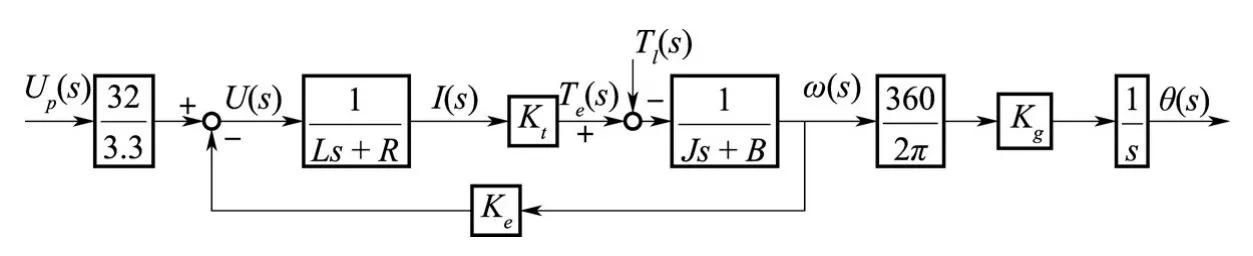
圖2 舵機動態(tài)結(jié)構(gòu)框圖Fig．2 The chart of actuator system

1.2 舵機控制策略分析

旋轉(zhuǎn)導(dǎo)彈的控制策略采用兩套控制系統(tǒng)，正確實現(xiàn)對導(dǎo)彈俯仰運動和偏航運動的控制，而導(dǎo)彈滾轉(zhuǎn)運動不加以控制，強制性的使其繞導(dǎo)彈的縱軸以一定的旋轉(zhuǎn)速度旋轉(zhuǎn)，靠尾翼斜置來保證固定的滾轉(zhuǎn)速率。

假設(shè)控制指令信號δc使產(chǎn)生水平向右的偏航力，如圖3 所示，則可以分解成兩路舵機的δ1和δ2;在一個自轉(zhuǎn)周期內(nèi)，δc的指令可分解成:

圖3 旋轉(zhuǎn)γ 時兩通道舵機示意圖Fig．3 The schematic diagram of spinning γ

電機功率、傳動機構(gòu)效率及結(jié)構(gòu)的轉(zhuǎn)動慣量、反饋回路中測量元件精度等一系列不可更改的因素，使得系統(tǒng)不可避免的帶來了幅值大小偏差，相角時機滯后等問題，從而形成了通道間耦合。在較大轉(zhuǎn)速下，當(dāng)彈體旋轉(zhuǎn)一定角度γ＇時，如圖4所示，舵機系統(tǒng)跟蹤指令仍是旋轉(zhuǎn)角度γ 的指令值，則會產(chǎn)生空間上控制力與控制力矩的偏差，造成其合力繞空間轉(zhuǎn)過一個γ＇- γ。

偏航方向上的作用力，由于延遲耦合到俯仰方向上。即偏航方向輸入的駕駛儀指令azc會導(dǎo)致俯仰方向出現(xiàn)相應(yīng)的等效ayc，這一額外的指令也會造成短周期響應(yīng)的穩(wěn)態(tài)偏差。

圖4 旋轉(zhuǎn)γ＇ 時兩通道舵機舵偏角Fig．4 Theschematic diagram of spinning γ＇

舵機系統(tǒng)的延遲是其固有特性，在高轉(zhuǎn)速的導(dǎo)彈中，指令周期很小，將被舵機延遲所吞沒，舵機沒有反應(yīng)，從而影響系統(tǒng)的控制品質(zhì)。所以旋轉(zhuǎn)導(dǎo)彈必須研究彈體和制導(dǎo)系統(tǒng)中各部分造成的交聯(lián)影響，以便采取適當(dāng)?shù)拇胧M行解耦，減小交聯(lián)影響。

2 導(dǎo)彈通道間耦合影響分析

旋轉(zhuǎn)導(dǎo)彈由于彈體繞彈體縱軸的滾轉(zhuǎn)導(dǎo)致了通道間的交聯(lián)，產(chǎn)生交聯(lián)的根本原因主要有:氣動交聯(lián)、慣性交聯(lián)及控制交聯(lián)。其中氣動交聯(lián)主要體現(xiàn)為馬格努斯效應(yīng)引起的面外力矩，慣性交聯(lián)主要表現(xiàn)為彈體的陀螺效應(yīng)，兩者屬于動力學(xué)耦合;控制交聯(lián)主要由安裝在彈體上的舵機系統(tǒng)的動力學(xué)延遲造成。

2.1 運動學(xué)耦合影響分析

馬格努斯效應(yīng)在彈體短周期運動達到穩(wěn)態(tài)時仍產(chǎn)生影響，陀螺效應(yīng)是一種輸出阻尼耦合，并在滾轉(zhuǎn)速度較低時對彈體穩(wěn)態(tài)效果影響不大。

對滾轉(zhuǎn)導(dǎo)彈方程進行線性化，彈體滾轉(zhuǎn)造成的馬格努斯效應(yīng)和陀螺效應(yīng)會導(dǎo)致彈體的輸出在空間存在一定的相位偏差，該偏差可以通過彈體的動力學(xué)模型得到，基于小擾動，系數(shù)凍結(jié)假設(shè)的導(dǎo)彈線性化模型:

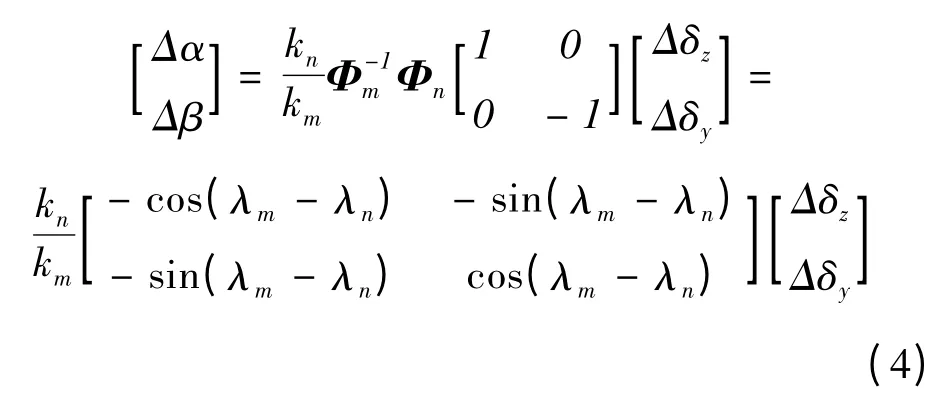
其中

λm的構(gòu)成包括了由于短周期穩(wěn)態(tài)馬格努斯效應(yīng)造成的耦合力矩、彈體主升力面提供的法向過載產(chǎn)生的機動對應(yīng)的陀螺力矩，正負由的符號決定，一般有λm＜0 ;λn是舵面升力提供的法向過載對應(yīng)的陀螺力矩產(chǎn)生的相位差，λn＞0 。由于舵面產(chǎn)生的法向過載系數(shù)a35一般遠小于彈體主升力面的法向過載系數(shù)a34，運動學(xué)耦合延遲角λα= λm-λn，因此λα的符號主要取決于λm的正負。

以某型導(dǎo)彈在Ma = 1.5 ，α = 1° ，γ = 0°(舵面呈“X”形狀)時的相關(guān)參數(shù)為例分析:

表1 模型導(dǎo)彈動力學(xué)參數(shù)Tab．1 Sample missile dynamics parameter

不同轉(zhuǎn)速對應(yīng)角度如表2 所示。

表2 各轉(zhuǎn)速對應(yīng)耦合角Tab．2 The couple angle for different conditions

從表中可以看到隨著轉(zhuǎn)速的增加，引起的耦合角度依次增加，λn本身極小，比λn高出好幾個數(shù)量級，隨著彈體的轉(zhuǎn)速變化λm變化甚微，λm的精度變化不足以影響控制效果。需要指出的是λn、λm的確依賴于彈體的氣動參數(shù)，在氣動參數(shù)的獲取中，辨識誤差相對較大，尤其是馬格努斯效應(yīng)的氣動參數(shù)的誤差是不可避免的。

2.2 舵機系統(tǒng)耦合影響分析

控制耦合，指因彈體旋轉(zhuǎn)使得兩路舵機控制通道相互影響的現(xiàn)象。控制耦合包括了指令解算的延遲時間和舵機系統(tǒng)延遲上，旋轉(zhuǎn)導(dǎo)彈的通道間耦合主要體現(xiàn)在舵機系統(tǒng)的時間延遲上。給舵機幅值為± 5°、頻率1 ～20Hz 的漸變線性正弦指令，處理實驗曲線，得到隨著彈體轉(zhuǎn)速變化，舵機滯后角度的關(guān)系見圖所示:

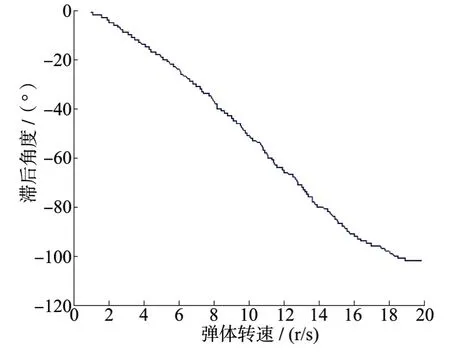
圖5 舵機滯后角度Fig．5 Actuator lag angle

相對運動學(xué)耦合，控制耦合對彈體通道間耦合影響更大，即舵機系統(tǒng)相位延遲較大。但對于舵機的動力學(xué)系統(tǒng)，通過大量地面試驗其系統(tǒng)參數(shù)辨識是能做到的。

3 舵機系統(tǒng)仿真分析與實驗驗證

對舵機系統(tǒng)中低頻段進行參數(shù)辨識，建立精確的數(shù)學(xué)模型。基于經(jīng)典控制理論，連續(xù)正弦掃頻，逼近了兩路舵機系統(tǒng)的二階數(shù)學(xué)模型:

兩路舵機模型差別不大，以下兩路舵機均采用D1(s)模型代替，得到幅值裕度，相角裕度;基于SISO 控制系統(tǒng)構(gòu)建校正環(huán)節(jié)，在控制器前向通路中加入串聯(lián)校正裝置，考慮到實際結(jié)構(gòu)與控制模型之間的差距，反復(fù)推敲中心頻率及開環(huán)增益降低的系數(shù)，確定中心頻率ωm=79.09rad/s，α =3.24 。

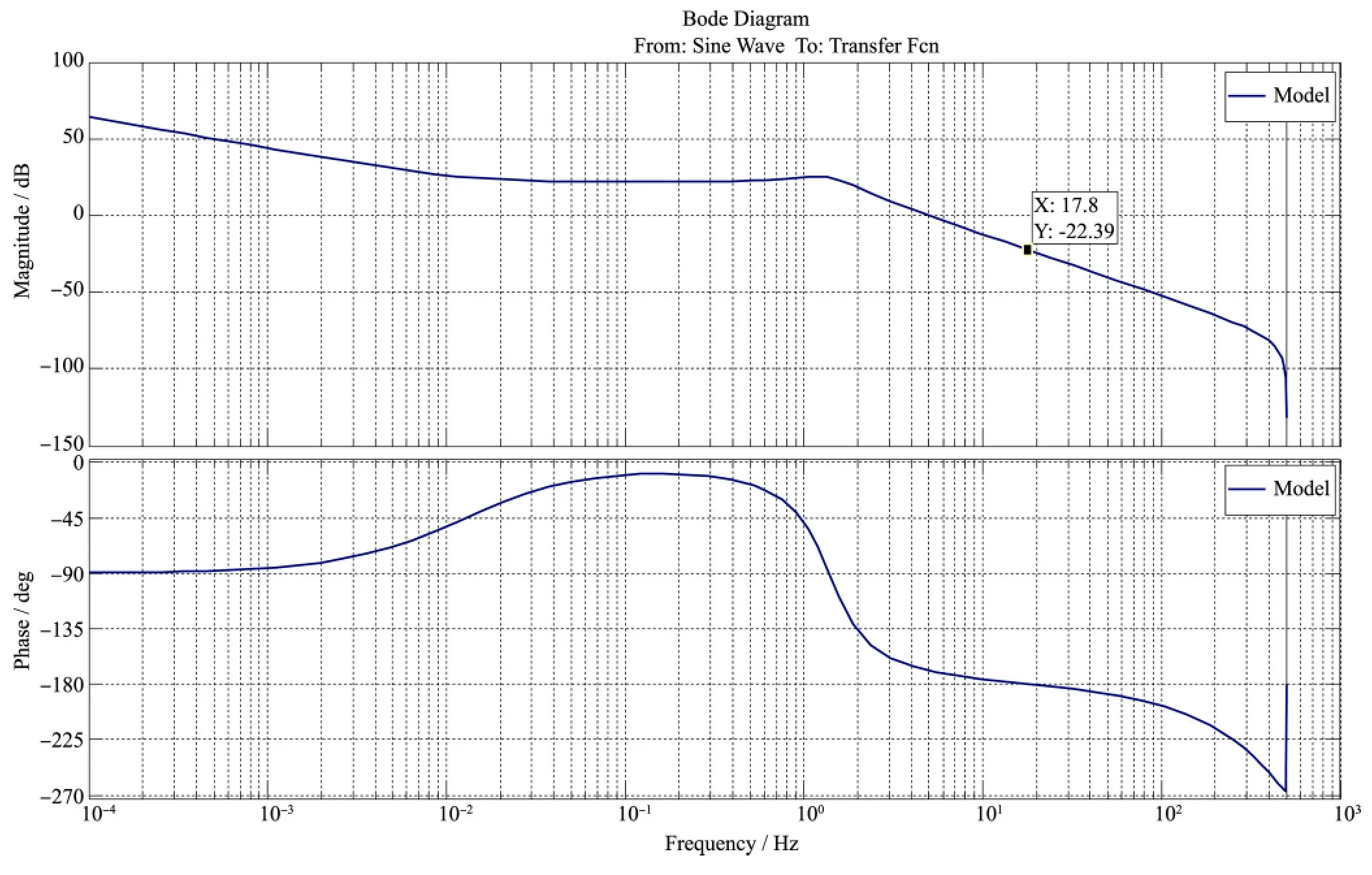
圖6 舵機開環(huán)數(shù)學(xué)模型仿真Fig．6 Simulation of actuator mathematical model

更好的方法則是，圍繞彈體轉(zhuǎn)速f 修正fm，fm對應(yīng)開環(huán)傳遞函數(shù)的相位超前頻率點，稍大于跟蹤頻率即所對應(yīng)閉環(huán)頻率點f。則ωm= 2πfm調(diào)整，α 值在控制系統(tǒng)穩(wěn)定的前提下取極大值。

對舵機系統(tǒng)進行實驗測試，得到其幅相頻特性如圖7 所示。

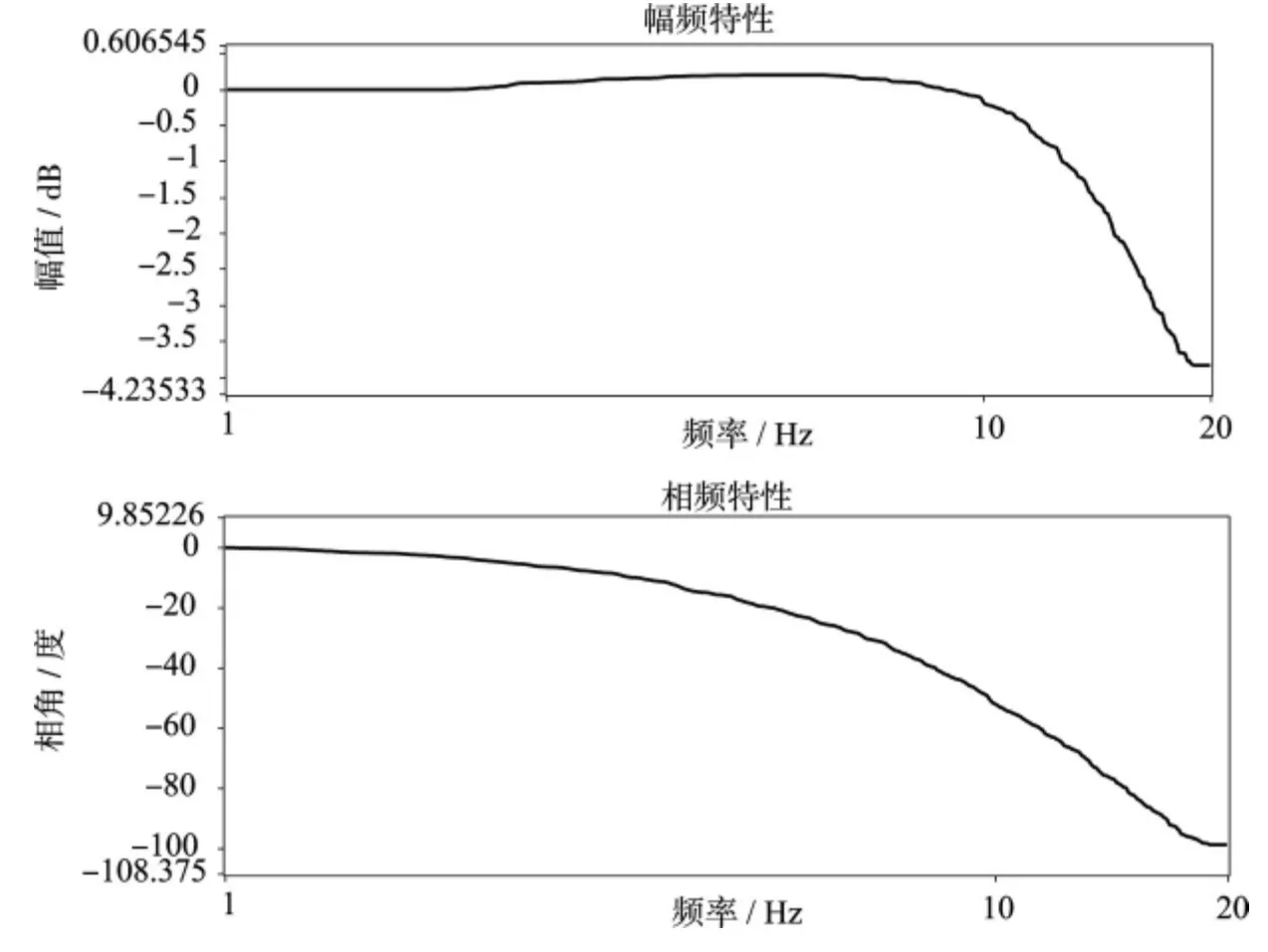
圖7 實驗顯示舵機閉環(huán)幅相頻特性曲線Fig．7 Character by the Frequency-Response Method

為解除導(dǎo)彈運動與制導(dǎo)系統(tǒng)產(chǎn)生的交聯(lián)，需使控制指令提前，加入指令補償，補償矩陣λδ中的γc與彈體轉(zhuǎn)速有關(guān)，根據(jù)速率陀螺測量值，并考慮指令延遲后獲得相應(yīng)補償矩陣值。

則對于彈體回路來說在舵機指令輸入端需要進行的相位補償角度為，其中γc為舵機動力學(xué)延遲角度，τ 為指令解算時間。

指令對舵機及系統(tǒng)純延遲的相位補償矩陣為:

而運動學(xué)中相位補償陣為:

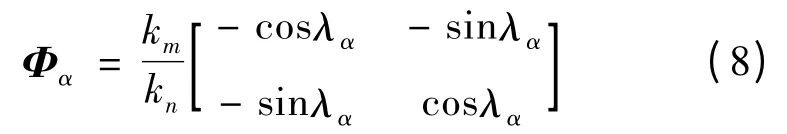
其中λα= λm- λn;

因此，動力學(xué)耦合與控制耦合，進行靜態(tài)解耦補償，則其舵機指令的補償矩陣為:

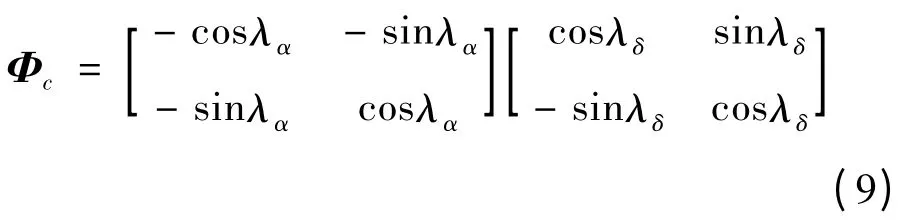
對m × m 維有理函數(shù)矩陣，令其元素為gij(s)(i，j = 1 ～m)定義對角優(yōu)勢度:

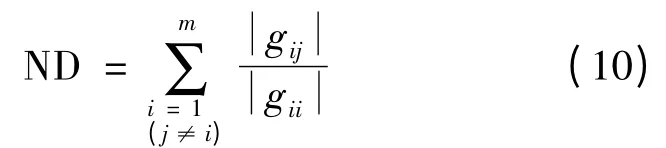
以4r/s 為例，理論上講總可以找一個補償矩陣，使得補償后多變量系統(tǒng)完全解耦，即非對角線元素為零，ND =0，但是這種補償矩陣可能具有十分復(fù)雜的形式，而且階次較高，實際應(yīng)用十分困難。

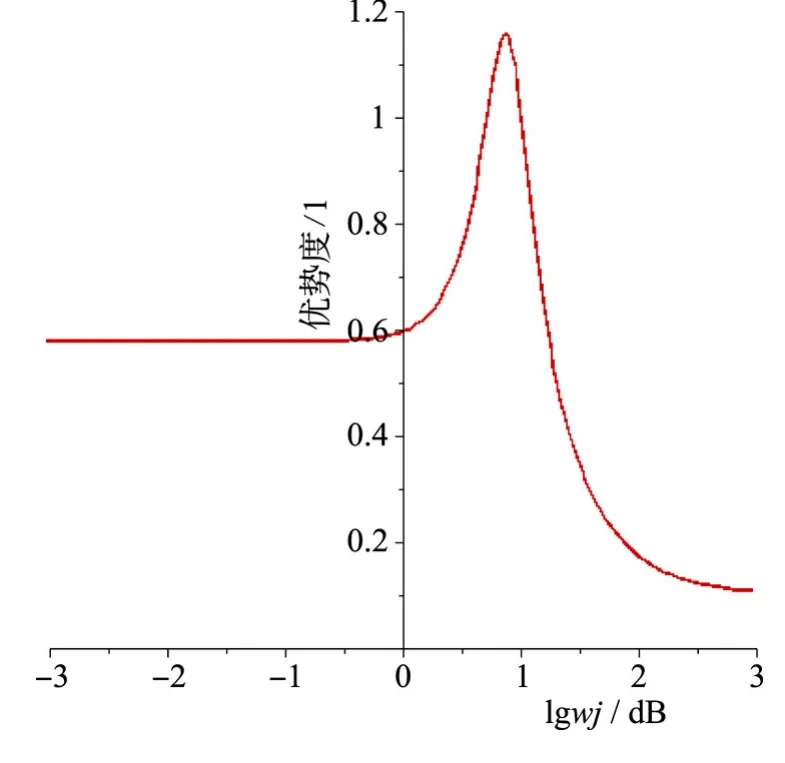
圖8 轉(zhuǎn)速4r/s 補償前優(yōu)勢度Fig．8 Superiority in 4r/s before compensation

加入轉(zhuǎn)速對應(yīng)λδ的預(yù)補償陣之后的對角優(yōu)勢圖形:

圖9 轉(zhuǎn)速4r/s 補償后對角優(yōu)勢度Fig．9 Superiority in 4r/s after compensation

多變量耦合系統(tǒng)中，設(shè)計中不需要實現(xiàn)系統(tǒng)完全解耦，只要求在工作頻段內(nèi)具有對角優(yōu)勢，為實現(xiàn)這一目的，非對角優(yōu)勢系統(tǒng)通常采用偽對角化方法，使得在低頻工作段具有對角優(yōu)勢。鑒于系統(tǒng)模型，是基于低頻段特性分析所得，所以解耦矩陣對低頻段效果明顯，對角元素具有較大的優(yōu)勢度，耦合作用減弱。使得系統(tǒng)工作頻率不必避開固有頻率，且最高耦合點向高頻移動，高頻段部分去耦效果不明顯，但工作頻段未涉及，對控制系統(tǒng)影響甚微。

4 結(jié)束語

工程算例中演算證明運動學(xué)造成的通道間耦合效應(yīng)極小，且隨轉(zhuǎn)速變化不大，基本維持在-1.55° 左右，所以如何有效消除控制耦合即舵機相角延遲，是雙通道控制解耦的重點。需要注意是在已知舵機控制系統(tǒng)相角延遲規(guī)律的情況下，才能實現(xiàn)解耦補償。驗證了n = 4r/s 時設(shè)計的預(yù)補償器能滿足良好的優(yōu)勢度，在其他轉(zhuǎn)速情況下，舵機延遲時間及彈體運動學(xué)耦合不一致，需重新查詢表格，設(shè)置預(yù)補償矩陣中λα和λδ。指令預(yù)補償矩陣的解耦方式，除了對舵機控制系統(tǒng)性能有足夠精確的測試，還對彈體滾轉(zhuǎn)角速度的反饋，馬格努斯力矩系數(shù)的辨識具有較強依賴性。結(jié)合控制器前端的動態(tài)超前網(wǎng)絡(luò)及指令預(yù)補償，可抵消小角度下的系統(tǒng)延遲，對于應(yīng)用雙通道正弦指令跟蹤的旋轉(zhuǎn)導(dǎo)彈，具有一定的工程價值。

［1］袁天保. 彈道導(dǎo)彈滾動飛行動力學(xué)與控制研究［D］. 長沙:國防科學(xué)技術(shù)大學(xué)，2005. ［YUAN Tian-bao. Study on dynamics and control of Spinning Ballistic Missile ［D］. Changsha:National University of Defense Technology，2005. ］

［2］閆曉勇，張成，楊樹興. 一類滾轉(zhuǎn)彈的補償解耦方法［J］.彈道導(dǎo)彈，2009，21 (4):17 ～25. ［YAN Xiao- yong，ZHANG Cheng，YANG Shu-xing. Decoupling Technique for a Class of Rolling Missile ［J］. Journal of Ballistics，2009，21(4):17 ～25. ］

［3］袁天保，劉新建，秦子增. 自旋彈道導(dǎo)彈動力學(xué)與控制［J］. 宇航學(xué)報，2006，27 (2):217 ～221. ［YUAN Tianbao，LIU Xin- jian，QIN Zi- zeng. Dynamic and control of Spinning Ballistic Missile［J］. Journal of Astronautics，2006，27 (2):217 ～221. ］

［4］錢杏芳，林瑞雄，趙亞男. 導(dǎo)彈飛行力學(xué)［M］. 北京:北京理工大學(xué)出版社，2000. ［QIAN Xing- fang，LIN Rui-xiong，ZHAO Ya-nan. Dynamics of Flight for Missiles［M］.Beijing:Beijing Institute of Technology Press，2000. ］

［5］孫春香. 旋轉(zhuǎn)彈雙通道控制系統(tǒng)的理論與工程技術(shù)研究［D］. 北京:北京理工大學(xué)，2012. ［SUN Chun- xiang.Study on the Theory and Technology of Double Channel Control System of Spinning Ballistic Missile［D］. Beijing:Beijing Institute of Technology.］