自適應高斯-勒讓德求積法

胡松巖

西南財經大學會計學院,四川成都610074

自適應高斯-勒讓德求積法

胡松巖

西南財經大學會計學院,四川成都610074

本文構造了自適應三點Gauss-Legendre求積算法，并初步對該算法和MATLAB自適應Simpson積分程序（quad函數）的計算效率進行了比較。數值結果表明:在同一精度下，該算法的計算成本大約是自適應Simpson積分算法的70%。

正交多項式;自適應Gauss-Legendre算法;自適應Simpson積分

積分是科學計算中經常遇到的問題之一。在數值積分的諸多算法中，辛普森算法是最常用的一種有效算法，許多著名的科學計算軟件中計算定積分的程序都是基于辛普森算法設計的。辛普森算法的一個突出優點是在積分區間逐步細分過程中，已經計算的節點的函數值可以重復利用。與辛普森算法相比，高斯——勒讓德積分法的優點是在節點數量一定的情況下具有更高的代數精度。然而，在積分區間逐步細分過程中，已經計算的節點的函數值難以重復使用。高斯積分雖然在積分計算中有諸多優點，并得到了廣泛應用[1-3]，但與辛普森算法相比哪一個計算效率更高還沒有見過報到。

本文，我們以三點高斯——勒讓德積分法為基礎，給出一種自適應數值積分算法，并與Matlab中的自適應辛普森積分法進行了數值比較。結果表明，自適應三點高斯——勒讓德積分法的計算成本大約是辛普森算法的70%，計算效率明顯高于辛普森積分法。

1 預備知識

1.1勒讓德正交多項式

定義1.1若f( x), g( x)∈C[ a, b]，ρ(x)為[a, b]上的權函數且滿足

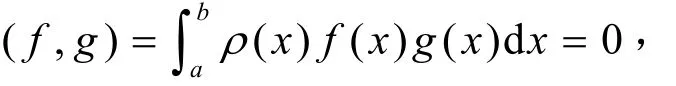
則稱f( x)與g( x)在[a, b]上帶權ρ(x)正交。若函數族φ0(x),φ1(x),…,φn(x ),…（有限個，或無限個）滿足關系

則稱｛φk(x)｝nj=0為[a, b]上帶權ρ(x)的正交函數族。

定義1.2設φn(x)是[a, b]首項系數an≠0的n次多項式，ρ(x)為[a, b]上的權函數，如果多項式序列｛φk(x )｝nk=0是正交函數族，則稱多項式序列｛φk(x )｝nk=0在[a, b]上帶權ρ(x)正交；稱φn(x)為[a, b]上帶權ρ(x)的n次正交多項式。

定義1.3在區間[1,1]-上關于權函數()1xρ≡的正交多項式稱為Legendre多項式。

1.2勒讓德求積公式

正交多項式的根都是單實根，且分布在相應的區間內。在求積公式

中，取n+1次勒讓德多項式的n+1個根作為積分節點x0,x1,…,xn，記lk(x)為拉格朗日插值基函數，即

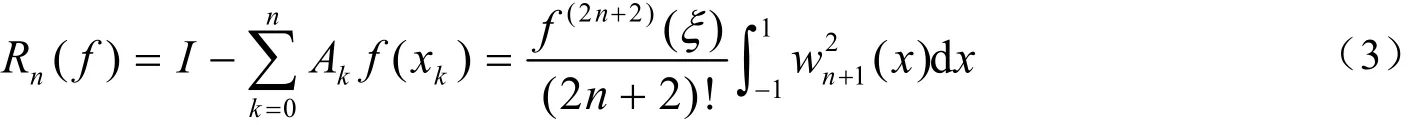
下面給出三點高斯——勒讓德求積公式。

取3次勒讓德多項式P3( x)=(5x3-3x)/2的三個零點作為積分節點，可得三點高斯-勒讓德求積公式

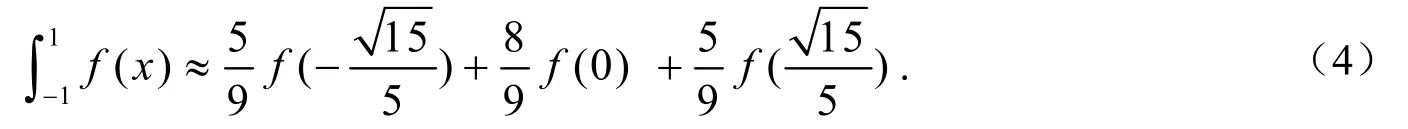
當積分區間不是[1,1]-，而是一般區間[,]a b時，只要作變換

即可得到

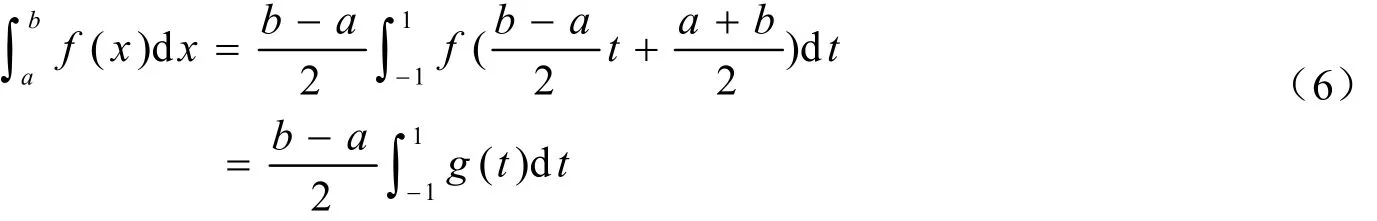
2 自適應高斯-勒讓德求積法

自適應積分法就是按照積分區間上被積函數變化的劇烈程度，動態調整積分節點的分布密度，以達到節約計算成本的目的。下面三次高斯——勒讓德正交多項式的根為節點，建立自適應的高斯——勒讓德求積格式。

記在積分區間[a, b]的某一子區間[di, di+1]上的三點高斯-勒讓德求積公式的積分值為

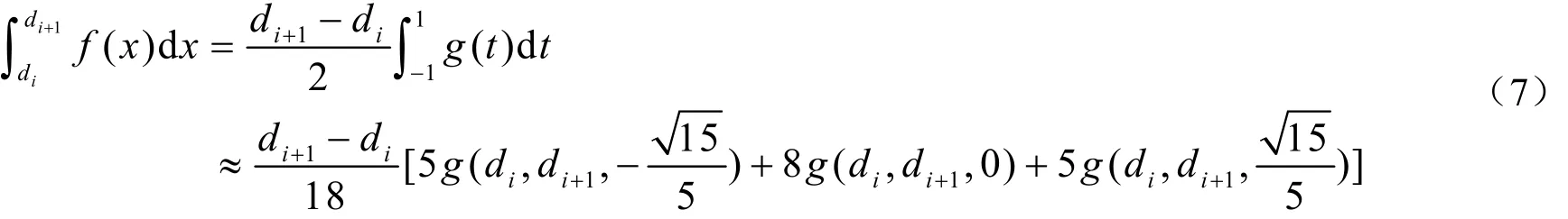
我們給出的自適應積分方法的基本思想是：整個區間[,]a b上的積分值()I f用多個子區間[di, di+1](i=0,1,…,m-1,d0=a, xm=b)上的三點高斯-勒讓德積分值之和來近似，

即

假定當前區間為[c1, c2]，令

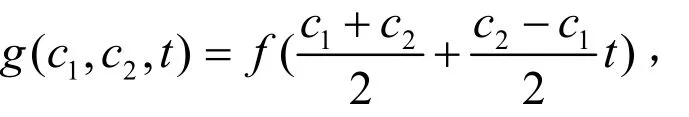
則

下面通過一定要求誤差來判斷區間是否細分，令

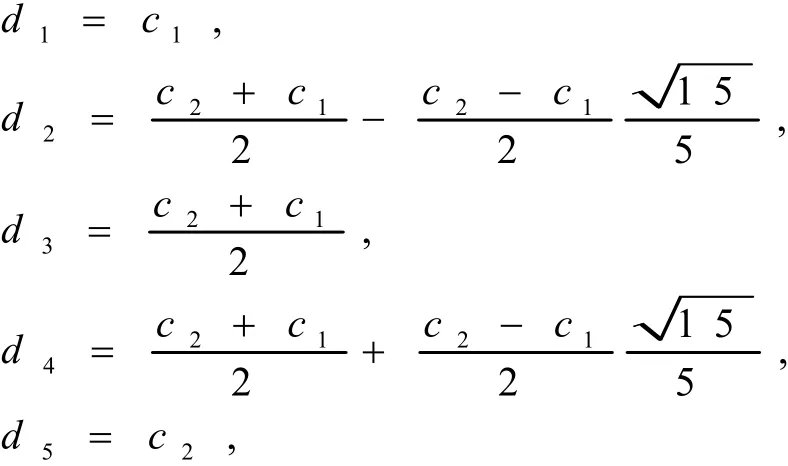
將區間[c1, c2]分成四個小區間[d1, d2],[d2,d3],[d3, d4],[d4,d5]，則

3 數值試驗

我們以被積函數的原函數能夠用初等函數表達的積分問題為例，通過10個算例對自適應高斯-勒讓德求積算法進行了積分精確性驗證.取ε=10-6，ε=10-8，采用雙精度計算，與Matlab中的自適應辛普森算法的計算量進行了比較。

取ε=10-6，ε=10-8（精確解為I=-1.42602475634627），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表1。

表1 例1在兩種控制精度下的計算結果Table 1 Results comparison of the two methods with different precisions on EX 1

取ε=10-6，ε=10-8（精確解為I=29.32621380439115），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表2。

表2 例2在兩種控制精度下的計算結果Table 2 Results comparison of the two methods with different precisions on EX 2

取ε=10-6，ε=10-8（精確解為I=0.57079632679490），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表3。

表3 例3在兩種控制精度下的計算結果Table 3 Results comparison of the two methods with different precisions on EX 3

取ε=10-6，ε=10-8（精確解為I=0.959572318005），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表4。

表4 例4在兩種控制精度下的計算結果Table 4 Results comparison of the two methods with different precisions on EX 4

取ε=10-6，ε=10-8（精確解為I=0.16666666666667），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表5。

表5 例5在兩種控制精度下的計算結果Table 5 Results comparison of the two methods with different precisions on EX 5

取ε=10-6，ε=10-8（精確解為I=13.28441557966756），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表6。

表6 例6在兩種控制精度下的計算結果Table 6 Results comparison of the two methods with different precisions on EX 6

取ε=10-6，ε=10-8（精確解為I=315.038461538461），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表7。

表7 例7在兩種控制精度下的計算結果Table 7 Results comparison of the two methods with different precisions on EX 7

取ε=10-6，ε=10-8（精確解為I=0.33333333333333），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表8。

表8 例8在兩種控制精度下的計算結果Table 8 Results comparison of the two methods with different precisions on EX 8

取ε=10-6，ε=10-8（精確解為I=0.54936030677801），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表9。

表9 例9在兩種控制精度下的計算結果Table 9 Results comparison of the two methods with different precisions on EX 9

取ε=10-6，ε=10-8（精確解為I=0.27219826128795），利用自適應三點高斯勒讓德算法以及自適應辛普森算法分別計算積分，計算結果見表10。

表10 例10在兩種控制精度下的計算結果Table 10 Results comparison of the two methods with different precisions on EX 10

4 結論與討論

本文基于三點高斯-勒讓德求積公式構造了一種自適應積分算法。根據我們的數值試驗，當計算精度為ε=10-6時，三點自適應高斯-勒讓德求積算法的平均計算量約為辛普森算法的71%；當計算精度為ε=10-8時，三點自適應高斯-勒讓德求積算法的平均計算量約為自適應辛普森算法的65%，由此可見新算法具有一定的實用價值。根據我們的數值經驗，兩點自適應高斯-勒讓德求積算法的計算效率遠比三點的算法低，甚至不如自適應辛普森算法，而四點及以上的自適應高斯-勒讓德求積算法將顯著增加子區間的分割數量，從而降低計算效率。因此，我們認為，三點自適應高斯-勒讓德求積算法在該類算法中，應該是最好的。

[1]李炯城,林惜斌,肖恒輝,等.高階高斯型積分計算機求解算法[J].計算機工程與設計,2012,33(5):1871-1875

[2]張慶禮,王曉梅,殷紹唐,等.高階高斯積分節點的高精度數值計算[J].中國工程科學,2008,10(2):35-40

[3]周立峰,吳明.用高斯積分法計算混油濃度[J].天然氣與石油,2005,23(5):4-6

Self-adaptive Gauss-Legendre Quadrature Method

HU Song-yan
School of Accounting,Southwestern University of Finance and Economics,Chengdu610074,China

In this paper,a self-adaptive three point Gauss-Legendre quadrature method was proposed and the efficiency of the method was compared with the program of QUAD in MATLAB preliminarily.In view of function evaluation times,the computation cost of the new method was almost 70 percentage of QUAD under the same precision.

Orthogonal polynomials;self-adaptive Gauss-Legendre quadrature method;self-adaptive Simpson-method

O241.4

A

1000-2324(2014)04-0610-05

2013-03-11

2013-03-20

胡松巖(1992-),女,漢族,山東棲霞人,本科生.