任意帶狀矩陣的求逆問題研究

鄧勇

任意帶狀矩陣的求逆問題研究

鄧勇

喀什師范學院數學系,新疆喀什市844006

對稱Toeplitz矩陣、Toeplitz矩陣以及三對角矩陣在數學的眾多領域有著廣泛應用,尤其是三對角或更一般的帶狀矩陣經常被應用于解偏微分方程的有限差分法和求解變系數線性遞歸方程等問題之中.所謂r-帶狀矩陣Br,n,(1≤r≤n)指的是當-r≤i≤r,1≤j≤r時元素為{aij},而剩下的其他元素全為零的n×n階矩陣且r稱為其帶寬.在已有文獻中,關于r-帶狀矩陣的許多特殊情況(r=1,2,3)的求逆問題已經得到徹底解決.為將這些結果一般化,對Mallik方法進行了推廣,并獲得了r-帶狀矩陣Br,n的LU分解和求逆(如果存在)公式.特別地,當r=n時,它成為計算可逆方陣逆矩陣的新途徑.

三角矩陣;Hessenberg矩陣;逆矩陣;r-帶狀矩陣

1 引言

目前，關于矩陣的求逆(如果存在)問題已有多種方法。例如：高斯——若當法、三角分解法、Cholesky分解法以及目前非常流行的分塊求逆法等[1,2,3,4]。眾所周知，對角矩陣A=diag( a1,…,an)的逆為A-1=進一步，若U是兩對角矩陣，設為：

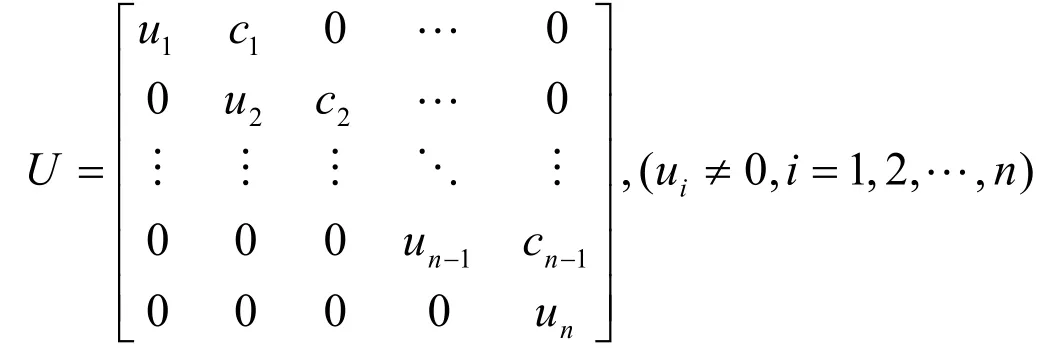
則U-1=(vij)，其中：

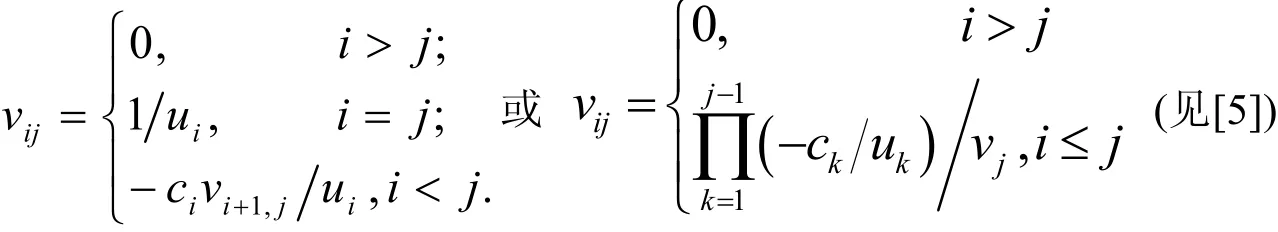
H B Li和M E Mikkawy等學者[6,7]證明了B-1=(cij)，其中：

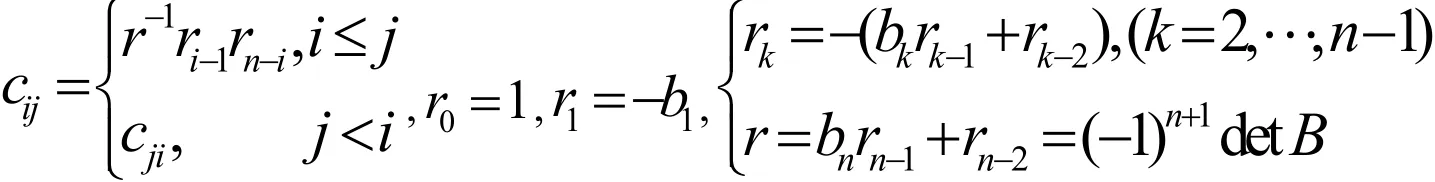
由此可見，三對角矩陣的逆矩陣是非稀疏的，因此，分塊求逆法對它不適用.基于這個原因，E Kilic利用反向連分數得到了三對角矩陣求逆的另一種特殊方法[8]。

一般地，我們定義n階r-帶狀矩陣,rnB為：

2 r-帶狀矩陣的LU分解

為獲得r-帶狀矩陣,rnB的LU分解，我們先構造兩個遞歸數列，對1ir≤≤和1sr≥≥，定義

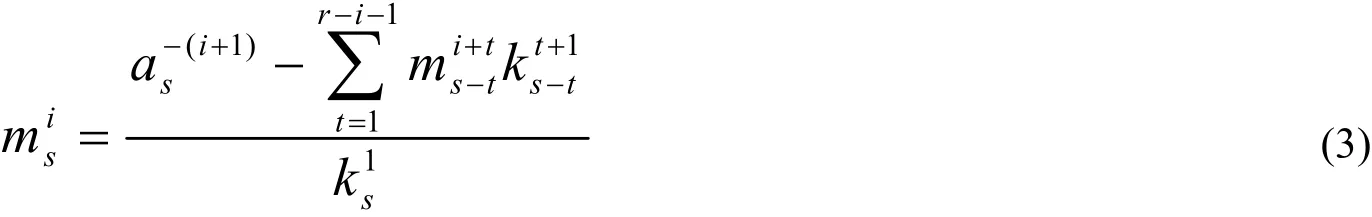
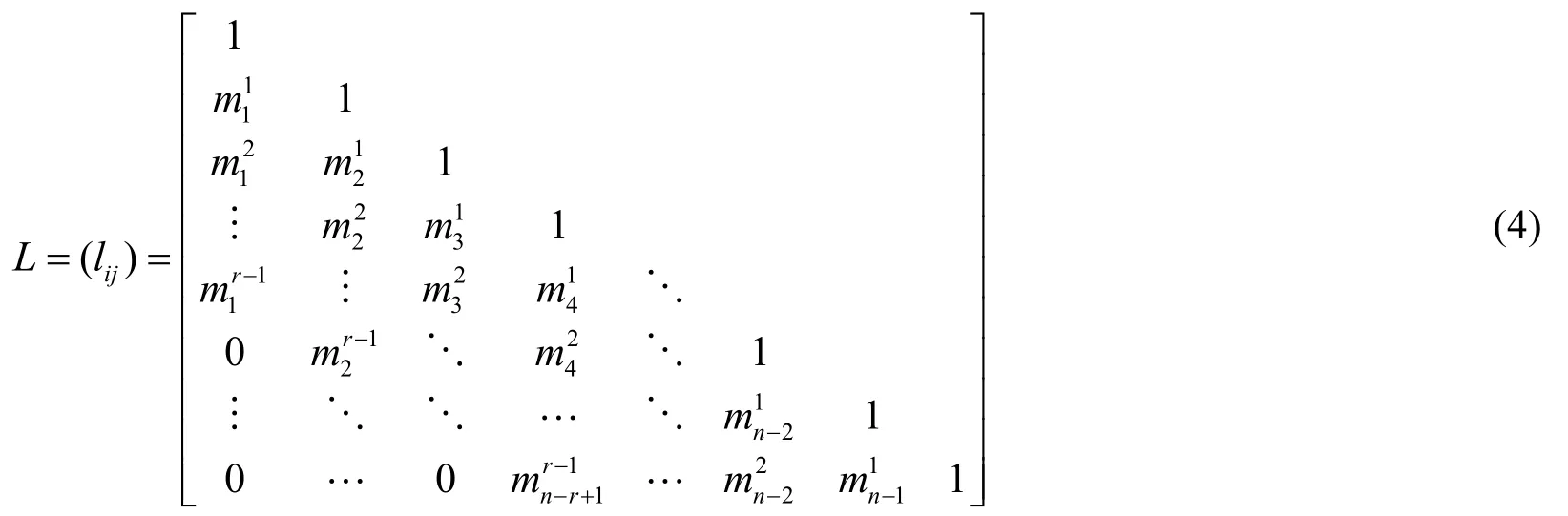
和

我就感覺這五個字非常厲害，任何矛盾和問題只要用上這五個字，立馬就能化掉百分之八十。不信你可以在生活中試驗一下，奇跡馬上就會出現。這可能就是導致成功者與失敗者兩種人生狀況的原因。

定理1當1n＞時，r-帶狀矩陣,rnB的LU分解為,rnBLU=，其中L和U分別由(4)和(5)所定義。

證明Ⅰ.考慮i=j的情況，當1≤i=j≤r 時，由矩陣乘法及L和U的定義，可得：

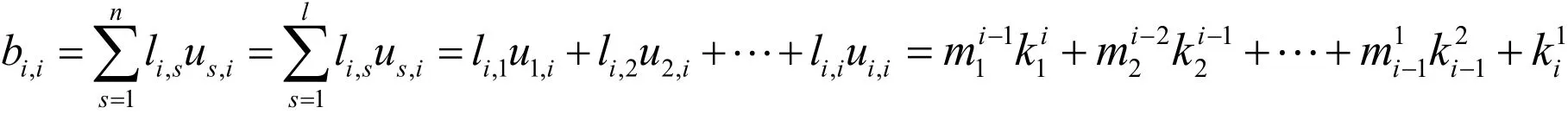
在(2)中取r=i，可得bi,i=a1i.當i=j＞r時，由矩陣乘法及L和U的定義，可得：

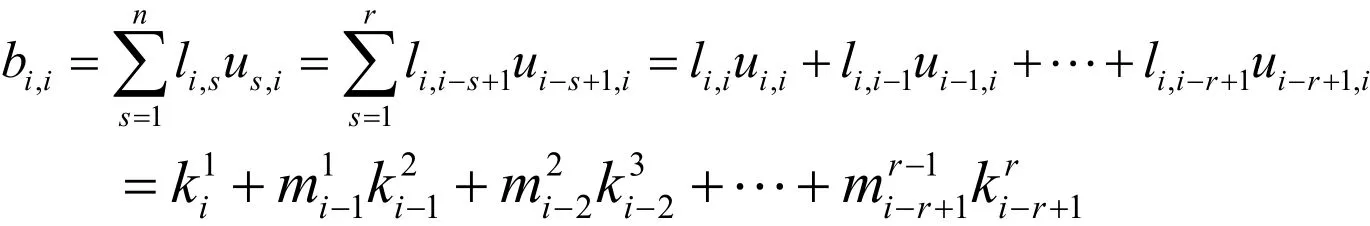
在(2)中取i=1，可得bi,i=a1n。綜上可知結論對i=j成立。

Ⅱ考慮ij≠且ji＞的情況，當jiq=+,11qr≤≤-時，由,rnB的定義，可知：

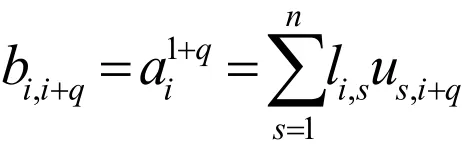
下面分兩種情況討論。首先，假設1≤i≤r-q ，因此有

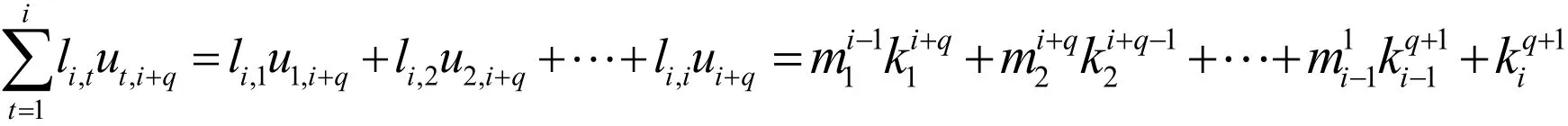
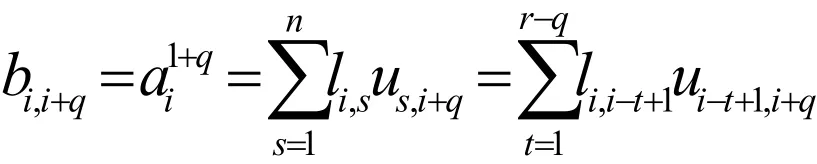
由矩陣U和L的定義，上式可寫成：

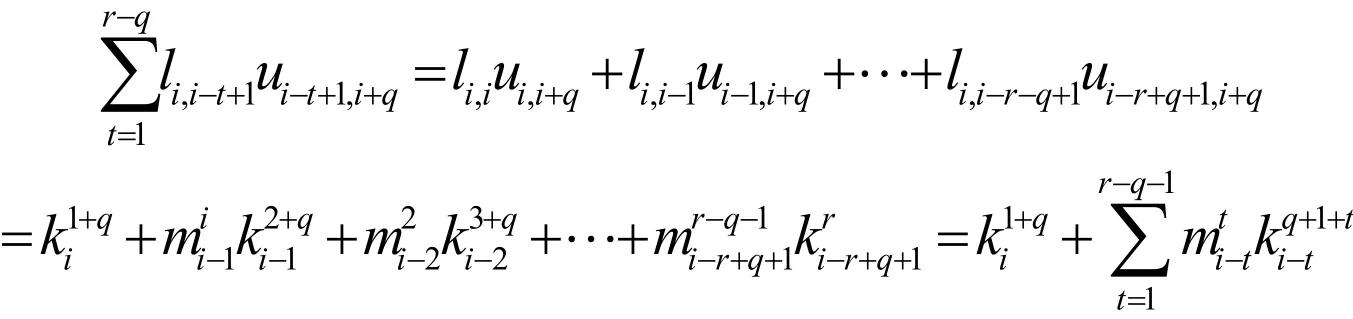
Ⅲ考慮i≠j且j＜i的情況，首先，設1≤i≤r-q ，由矩陣U和L的定義可得：

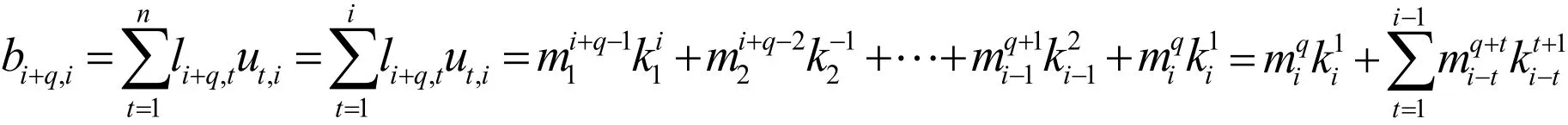
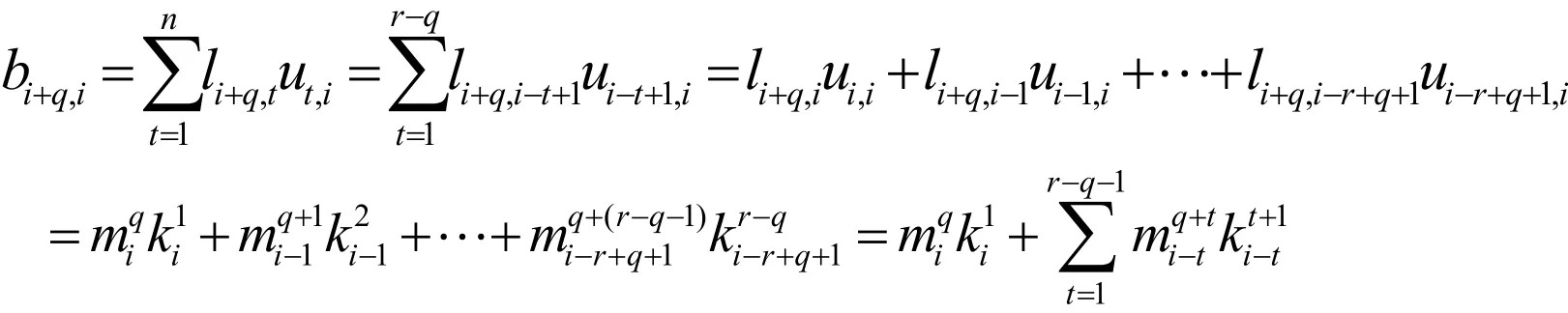
在(2)中取n=i和i=q，可得b=a-(q+1)，證畢。

i+q, ii

注：若在矩陣,rnB中取rn=,則定理1的結果對任意方陣的LU分解都有效。

由Br,n的LU分解立即可得det(Br,n)的一個計算公式，即

3 三角形矩陣的逆

為獲得一般三角形矩陣的求逆公式，我們先構造三角形矩陣的Hessenberg子矩陣，并計算其行列式,進而確定三角形矩陣的逆矩陣元素。這里只討論上三角形矩陣的情形，對下三角形矩陣類似可得。設H=(hij)是任意n× n階上三角形矩陣.對s＞r＞0，刪去H的前r列與后n-s列及前r-1行與后n-s+1行后所得到的s-r階子矩陣稱為H的上Hessenberg子矩陣，記作Hu(r, s)=()。顯然，H的(s-r)×(s-r )階上Hessenberg子矩陣Hu(r, s)具有如下形式：

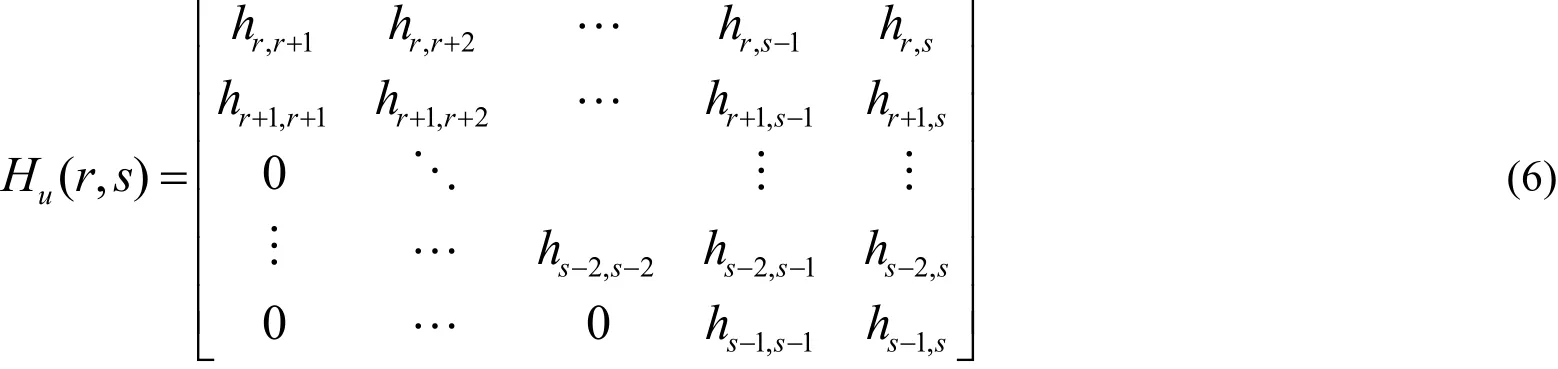
類似地，設H=(hij)是任意n× n階下三角形矩陣。對r＞s＞0，刪去H的前r行與后n-s行及前r-1列與后n-s+1列后所得到的r-s階子矩陣稱為H的下Hessenberg子矩陣,記作.顯然,H的(r-s)×(r-s )階下Hessenberg子矩陣Hl( r, s)具有如下形式：

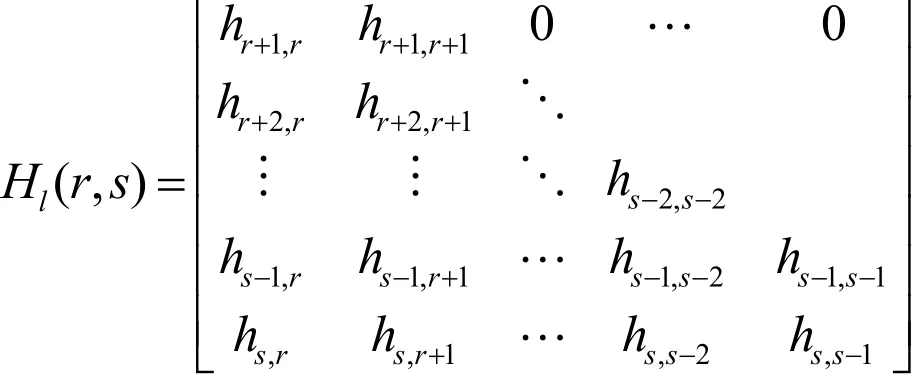
引理1設(j-i)×(j-i )階上Hessenberg矩陣Hu(i, j)由(6)所定義，則對j＞i+1，有

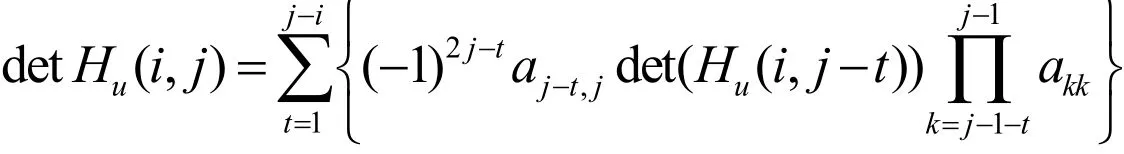
證明只需對最后一列用Laplace展開定理計算上Hessenberg矩陣Hu(i, j)的行列式即可，證畢。

定理2設U=(aij)是任意n× n階上三角形矩陣.若W=(wij)=U-1是它的逆矩陣，則

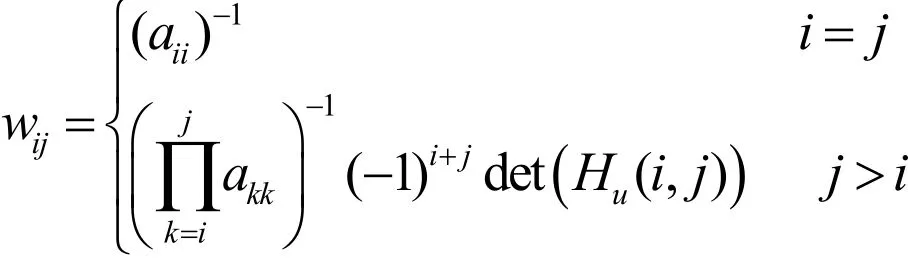
其中Hu(r, s)如前所述。

證明設WU=E=(eij)，顯然，當i=j時，E=In是n階單位矩陣.當j＞i時，由矩陣W和U的定義，可得：

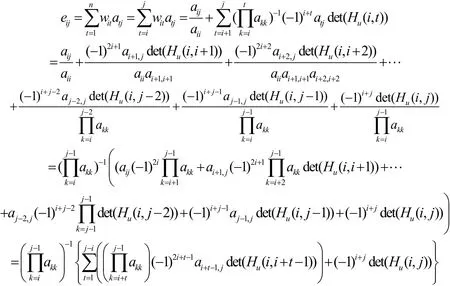
由引理1，可得eij=0，證畢。

4 r-帶狀矩陣的求逆公式

為獲得r-帶狀矩陣的求逆公式，只需求出下三角形矩陣L和上三角形矩陣U的逆即可。為此，由定理2可得引理2和引理3。因它們的證明只需代入直接驗證,故在此省略。

引理2已知下三角形矩陣L由(4)給出.若E=(eij)表示L的逆，則：其中Ll( i, j)如前所定義。

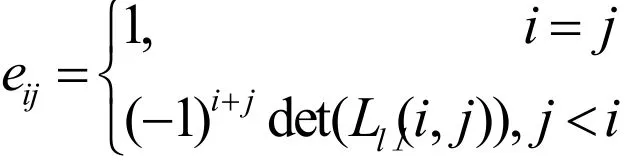
引理3已知上三角形矩陣U由(5)給出。若G=(gij)表示U的逆，則：

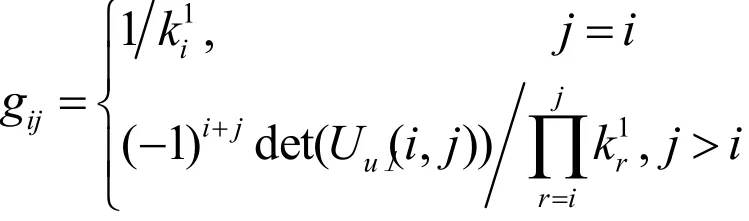
其中Uu(i, j)如前所定義。

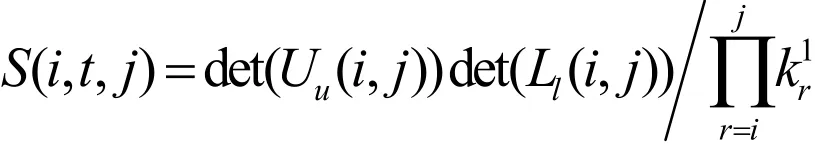
則：

證明：因為,rnBLU=，由引理2、3，可得別取i＜j, i=j, i＞j 三種情況，并將引理2、3中git,etj的表達式代入驗證即可得證，證畢。

[1]趙立群.一些稀疏矩陣的逆和行列式的計算[D].福建:閩南師范大學數學與統計學院,2011

[2]陳芳,徐仲,陸全.分塊帶狀矩陣的逆[J].高等學校計算數學學報,2006,28(3):209-215

[3]楊明順.三角矩陣求逆的一種方法[J].渭南師范學院學報,2003,18(5):12-13

[4]蘇連存.高階矩陣分塊求逆的一組公式及應用[J].青海大學學報(自然科學版),2002,20(5):62-65

[5]王美蓮,何翠竹.一類特殊矩陣的逆矩陣的特點及求逆公式[J].忻州師范學院學報,2010,26(2):42-43

[6]H B Li,Huang T Z.On the inverses of general tridiagonal matrices[J].Linear AlgebraAppl,2010,433(5):965-983

[7]Mikkawy M E,Karawia A.Inversion of general tridiagonal matrices[J].Appl Math Lett,2006,19(4):712-720

[8]Kilic E.Explicit formula for the inverse of a tridiagonal matrix by backward continued fractions[J].Appl Math Compute,2008,197(6):345-357

[9]呂小光.關于Toeplitz矩陣的計算[D].成都:電子科技大學數學科學學院,2007

[10]Mallik R K.The inverse of a tridiagonal matrix[J].Linear AlgebraAppl,2001,325(2):109-139

The Inverse Problems Research ofArbitrary Banded Matrix

DENG Yong
Department of Mathematics,Kashgar Teacher's College,Kashgar844006,China

The inverses ofr-banded matrices,forr=1,2,3 have been completely resolved as one can see from the references. LetBr,n,(1≤r≤n)be ann×nmatrix of entries{aij},(-r≤i≤r,1≤j≤r),with the remaining un-indexed entries all zeros.In this paper, generalizing a method of Mallik,we give theLUfactorization and the inverse of the matrixBr,n(if it exists).Our results are valid for an arbitrary square matrix(takingr=n),and so,we will give a new approach for computing the inverse of an invertible square matrix.

Triangular matrix;Hessenberg matrix;inverse matrix;r-banded matrix

O151.21

A

1000-2324(2014)04-0620-06

2013-03-22

2013-04-25

國家社科基金項目(11XTJ001)

鄧勇(1967-),男,四川遂寧人,教授,碩士生導師,主要從事矩陣及其數值研究.Email:dengy-ks@sohu.com