應用角動量升降算符分析角動量的矩陣表示和表象變換

田杏霞，王 鵬，王 艷

(通化師范學院 物理學院，吉林 通化 134002)

在量子力學中，算符和波函數的具體表示形式由選擇的表象決定．同一個算符在兩個不同表象之間的表示可以通過變換矩陣換算，但在角動量問題中，角動量分量的矩陣表示并不容易求得，本文利用升降算符計算角動量的矩陣表示，以及不同分量表象之間的變換[1-2]．

1 角動量升降算符

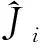
(1)

(2)

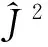
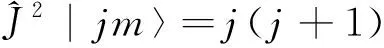
(3)

(4)

1.1 升降算符的定義

定義算符

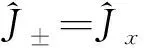
(5)

升降算符與角動量分量滿足如下關系：

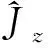
(6a)

(6b)

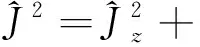
(6c)

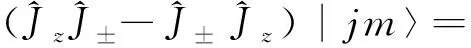
(7)

1.2 升降算符對波函數的作用

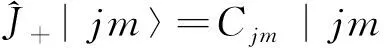
(8)

(9)

將(9)式左作用于(8)式，我們可以得到：

(10)

將(6c)式代入上式的左邊進行整理，得到：

與(10)式對比，得：

|Cjm|2〈jm+1|jm+1〉=
(j(j+1)?2-m2?2-m?2)〈jm|jm〉

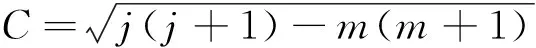
所以升降算符對波函數|jm〉的作用：

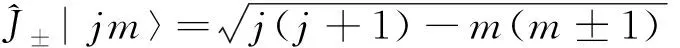
(11)

2 利用升降算符建立表象的變換矩陣

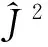
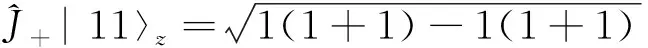
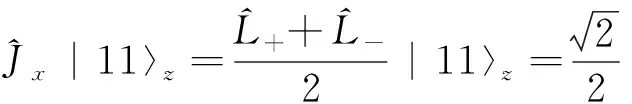
(12a)

(12b)

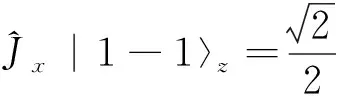
(12c)

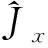
(13)

(14)

|1m〉x=c1|11〉+c2|10〉+c3|1-1〉

(15)

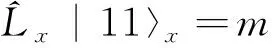
同理可得：

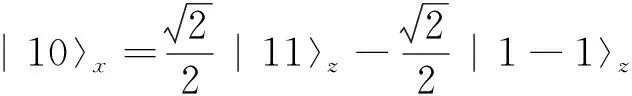
根據表象變換矩陣元的定義[1,2]，我們可以得到從z表象到x表象的變換矩陣為：

(16)

按照同樣的方法可以知道從z表象變到y表象的變換矩陣為：

(17)

3 總結

求解角動量算符的矩陣表示和

分量表象之間的變換矩陣的方法有很多，每一種方法都有自己的優點和缺點．本文通過引入升降算符，用簡單的計算給出了角動量分量算符在z表象中的表示，同時推導了從z表象到x(y)表象的變換矩陣．在文中以j=1為例，這一方法可以推廣j為任何值的情況．

參考文獻：

[1]周世勛.量子力學教程[M].北京:人民教育出版社，2009：94-117.

[2]曾謹言.量子力學[M].北京:科學出版社，2007:251-256.

[3]馬宇曉.量子數l的上升算符和下降算符對|l，m〉的作用[J].大學物理，2002(09).